测边网坐标平差的加性乘性混合型误差模型解算

王乐洋,胡芳芳

(1.东华理工大学 自然资源部环鄱阳湖区域矿山环境监测与治理重点实验室,南昌 330013; 2.东华理工大学 测绘与空间信息工程学院,南昌 330013)

加性乘性混合型误差模型在大地测量领域前进的步伐未曾停止。在20世纪早期,Helmert[1-2]首次提及了加性误差模型,引入了大地测量观测标准误差的概念;到20世纪中期,考虑到观测误差的比值是恒定的而不是方差,Kneissl[3-4]引入了乘性误差模型的概念;20世纪80年代,Wübbena[5-7]提出了用于GPS观测调整的组合模型的概念,将加性误差模型和乘性误差模型扩展为允许在单一模型中考虑两种类型误差的加性乘性混合型误差模型。

此后学者对于加性乘性混合型误差模型的研究不断深入[8-15]。文献[8]通过改变直线拟合算例中点的质量验证了文中所提出的偏差改正最小二乘方法与拟似然函数法的等价性,同时还验证了该方法具有二阶无偏性。文献[9]推导出了文献[8]中所提出方法的精度评定公式,通过模拟一个用激光雷达测量的滑坡模型验证了偏差改正加权最小二乘方法比普通最小二乘方法的性能要好很多。文献[10]通过模拟的直线拟合模型和数字高程模型(digital elevation model,DEM)验证了Sterling插值方法可以使乘性随机误差模型的精度评定方法的精度达到二阶。文献[11]增加了一个真实的病态DEM数据案例来验证文中提出的比例无迹变换(scaled unscented transformation, SUT)精度评定方法能够得到更准确的参数估计且该算法在大地测量领域的适用性也更强。文献[12]和[13]通过模拟的直线拟合模型和DEM模型验证了更加符合现代大地测量手段的加性乘性混合型误差模型的参数求解方法的有效性,其中偏差改正加权最小二乘法是二阶近似无偏的,精度最好。之后,文献[14]和[15]将加性乘性混合型误差模型和智能优化算法相结合,通过模拟的直线拟合模型和改进的DEM模型验证了两者相结合后可以得到更快的收敛速度、更优的参数估值和更合理的精度信息。

以上对于加性乘性混合型误差模型的参数估计方法的算例当中鲜少提及使用测边网坐标平差算例来进行验证。测边网坐标平差模型用于测量边长的测距仪的标准精度可以表示为:σSi=a+bSi,其中a和b可以很好的对应于加性乘性混合型误差模型当中的加性随机误差和乘性随机误差。测边网坐标平差模型是大地测量领域广泛采用的数学模型,是一种利用边长测量的观测方法,其主要应用于对由大量测量边长组成的测边网进行处理。显而易见,距离测量相对操作简单可行,每一条边长的观测时间均较短,同时测边网坐标平差模型被广泛应用于确定区域内各个测量点的坐标,这对于地图绘制、土地规划和建筑工程等领域具有极大的实用价值。此外,该模型还能够有效地校正测量误差,提高测量精度。因此,对于测边网坐标平差的加性乘性混合型误差模型解算的研究十分有必要。

1 加性乘性混合型误差模型及其求解

已有文献中研究的加性乘性混合型误差模型的数学表达式为[12]:

y=f(β)⊙(1+εm)+εa.

(1)

式中:y∈Rn×1表示观测值向量;f(β)表示未知参数的函数;β∈Rt×1表示未知参数向量;n为观测值数量,t为未知参数个数; ⊙表示向量或矩阵的哈达玛乘积符号;1∈Rn×1表示元素全为1的列向量;εm∈Rn×1表示服从正态分布的随机乘性误差列向量;εa∈Rn×1表示服从正态分布的随机加性误差列向量。

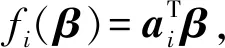
y=Aβ⊙(1+εm)+εa.

(2)

E(y)=Aβ.

(3)

由式(2)和式(3)可得观测值y的方差协方差阵为:

Dy=E[(y-E(y))(y-E(y))T]T=

(4)

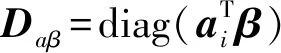
将最小二乘准则应用到式(2)的加性乘性混合型误差模型当中,可以得到目标函数的表达式为[13]:

min:F(β)=(y-Aβ)TP(y-Aβ).

(5)

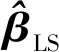
(6)

(7)

式中:

(i=1,2,…,t).

(8)

(9)

单位权中误差的估计式为:

(10)

2 测边网坐标平差的加性乘性混合型误差模型解算

测边网是一种测量地面上点的方法,然而由于仪器误差、环境条件和人为因素等各种因素的影响,测量数据可能存在误差。为了提高测量精度,需要进行坐标平差。而坐标平差则是指在已知部分点的坐标和测量距离的情况下,通过数学方法计算出其余点的坐标,使得测量距离的观测值与计算值之间的差异最小。

测边网由一系列相互连接的点组成。其中,一些点的坐标事先已知,而其他点的坐标未知。已知点称为控制点,未知点称为挂点。相邻点之间的距离和角度测量是测边网的基础。本文将选用参考文献[16]中的例7～10来进行计算,该测边网的基本计算步骤如下[16]:

1)根据所给已知点的坐标和已知测距边长的信息,由边长交会计算出待定点的近似坐标。如图1所示,A,B,C,D为4个已知点,P1,P2,P3,P4为4个待求点,1～13为通过测距仪观测得到的13条边长,分别记为L1～L13,则待定点的近似坐标为:

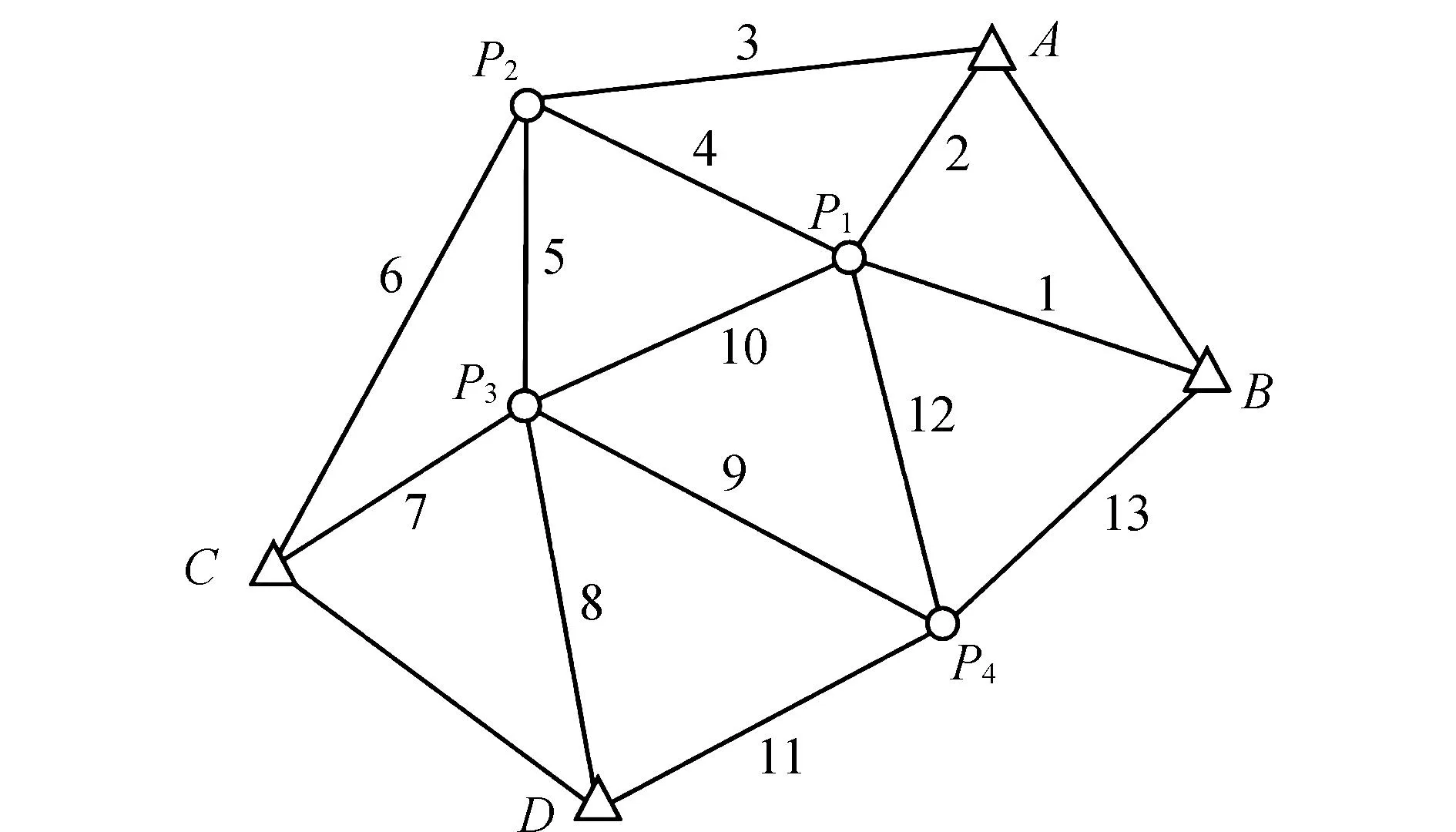
图1 测边网示意图

(11)

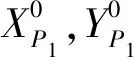
2)由已知点坐标和求解得到的待定点近似坐标计算出误差方程的系数和常数项,列出整个网的误差方程,误差方程的个数对应测距仪所测得的边长的个数。其中边L2即边AP1的误差方程为:

(12)

(13)

其中:

l4=L4-SP1P2。

同理,可得到边长L5,L9,L10,L12的误差方程。

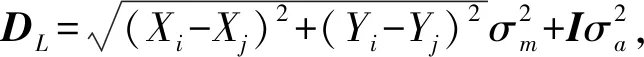
4)由步骤1)～3)所求得的信息组成法方程求解待定点的坐标改正值。根据步骤1)列出所有的误差方程后可得到误差和方程:

(14)

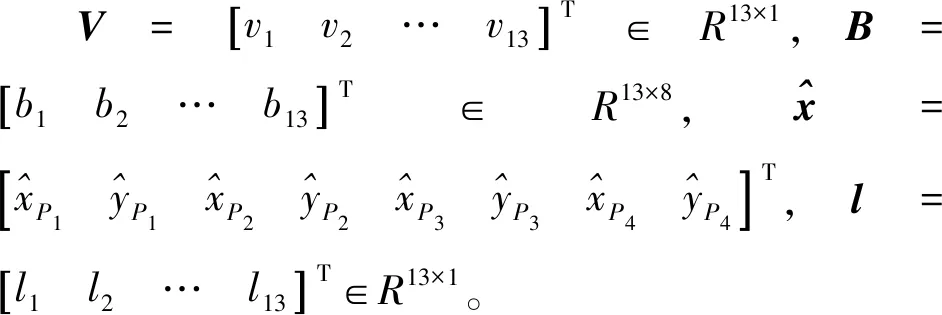
5)将待定点的近似坐标与待定点的坐标拟合值相加得到待定点的坐标平差值结果,求解单位权中误差。

3 算例与分析

本文选用文献[16]中的例7～10,采用测距精度为σs=3+1×10-6S的某测距仪观测了13条边长(S为测量边长)。表1为已知点坐标,表2为观测边长。

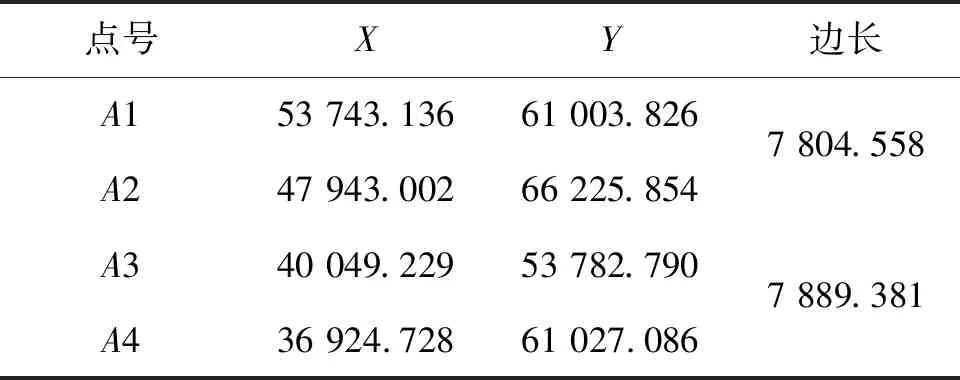
表1 已知点坐标 m

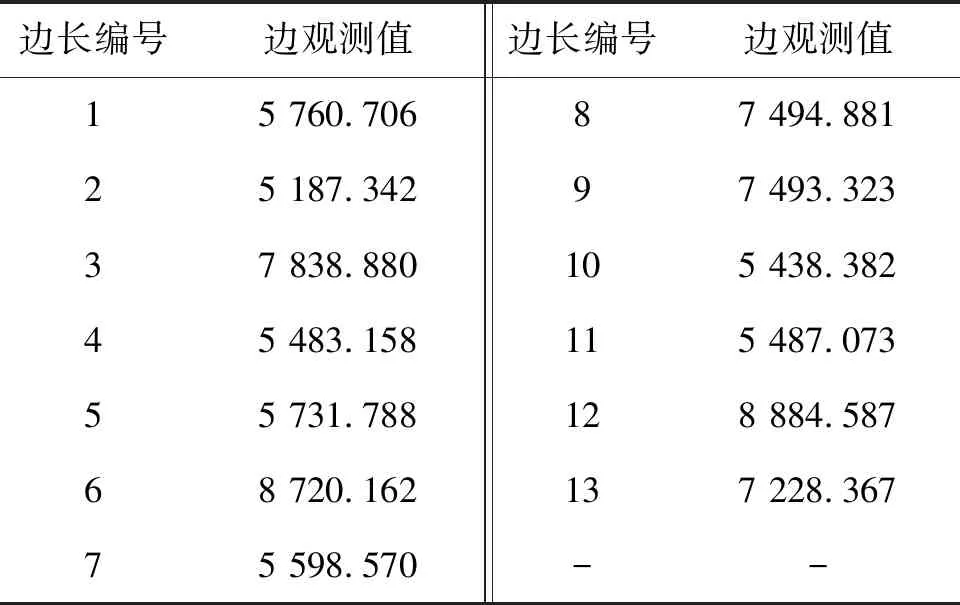
表2 观测边长 m

根据表1的已知点坐标和表2的观测边长,通过勾股定理和边长交会可以求解出4个待求点的近似坐标分别为:P1(48 580.270,60 500.505)m,P2(48 681.390,55 018.279)m,P3(43 767.223,57 968.593)m,P4(40 843.219,64 867.875)m。根据待定点P1,P2,P3,P4的近似坐标和已知点A,B,C,D的坐标求解出组成误差方程的相关数据;若误差方程计算过程中涉及到点A,B,C,D的坐标则选用式(12)计算,其余误差方程的计算选用式(13)。求得该算例的误差方程为:

(15)

其中待求的误差改正数和测量长度平差值的单位均为mm。

根据文献[16]中的例7～10的测距仪的标准精度σs=3+1×10-6S设置本算例中的加性乘性混合型误差模型中的随机乘性误差的标准差为1×10-3mm和随机加性误差标准差为3 mm,令单位权中误差为10 mm,观测值的方差协方差阵由式(4)计算得到。使用本文提到的测边网坐标平差的加性乘性混合误差模型的WLS和bcWLS方法对待定点P1,P2,P3,P4的坐标平差值进行计算,求解得到的坐标改正值和单位权中误差估值结果见表3,待求点点位中误差结果见表4。

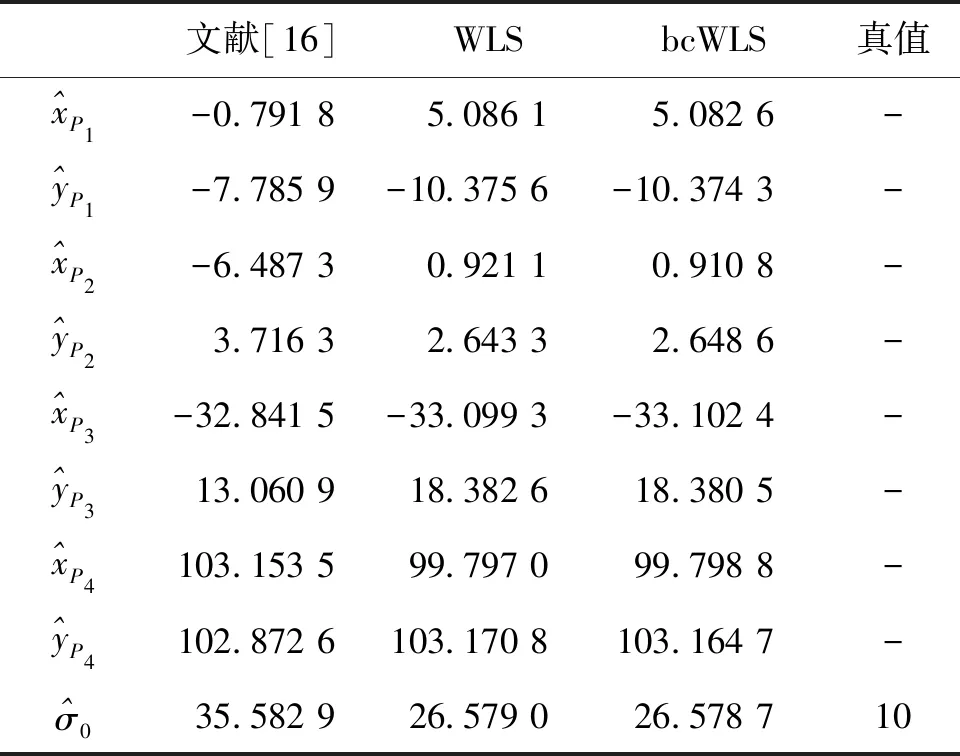
表3待求点坐标改正值和单位权中误差估值 mm

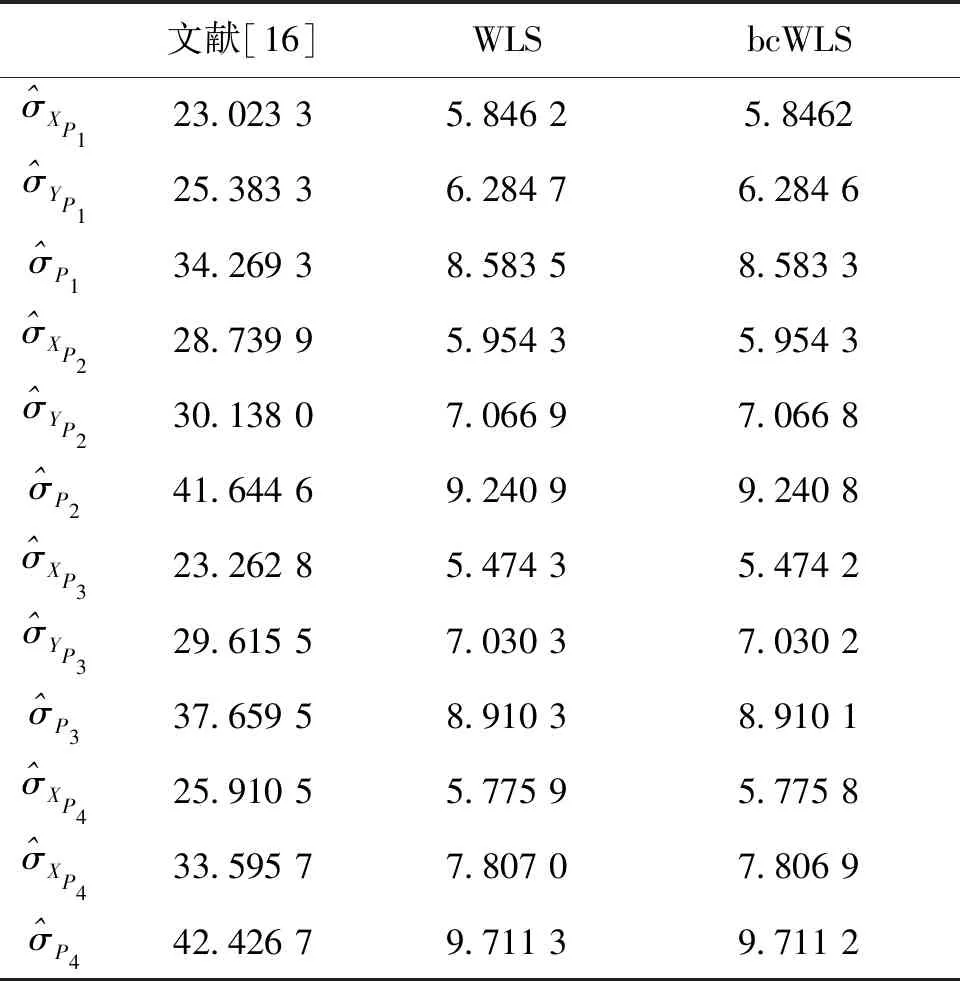
表4 待求点点位中误差 mm

如表3可知,本文所推导测边网平差模型的加性乘性混合型误差模型的WLS和bcWLS方法所求得单位权估值与设定的真值更加接近,且三种方法中的bcWLS所求得的结果最优。通过本文的WLS方法所求得的单位权估值比文献[16]中的方法所求得的单位权中误差估值提高了25.304%,通过bcWLS所求得的单位权估值比文献[16]中的方法所求得的单位权中误差估值提高了25.305%。通过本文的WLS和bcWLS方法所求得的待定点的坐标平差值与文献[16]中的方法所求得的结果不相同,在点位P1和P2的x方向的坐标改正值结果与文献[16]的结果相差明显,在点位P2和P4的y方向的坐标改正值结果与文献[16]的结果差距较小。

如表4可知,本文所推导的WLS和bcWLS所求得待定点的点位中误差更小,精度更高;这是因为文献[16]中的WLS所选用的权值与测距仪所测得的边长有关,这些边长均是含有误差的,而本文的WLS所选用的权值根据文献[16]中所求得的结果进行了一定的修正,bcWLS方法则进一步修正了WLS方法中的偏差项,因此通过bcWLS方法所求得的待定点坐标中误差最小,精度最高。

4 结 论

现代大地测量数据处理领域当中的误差模型大多为加性乘性混合型误差模型。为了使该模型在处理实际数据时更具有优势,本文首次引入加性乘性混合型误差模型进行测边网平差。通过实验计算分析,表明加性乘性混合型误差模型的WLS和bcWLS可以对根据测量值所得到的不正确的权值加以改正,通过本文所推导的WLS和bcWLS方法可以得到更准确的坐标改正值且得到的坐标改正值精度更高。