基于ConvLSTM的北京区域电离层延迟建模

谭宗佩,白征东,张 强,郭锦萍,段博文

(清华大学 土木工程系,北京 100084)

电离层延迟是 GNSS定位中一种十分常见的误差。这个偏差量主要与信号传播路径上的总电子含量(total electron content,TEC)有关。而TEC可由天顶方向的总电子含量(vertical total electron content,VTEC)计算得出。

电离层延迟常用的改正方法包括 Klobuchar模型[1]、全球格网模型、多频改正等[2-4]。Klobuchar模型可用于单频电离层延迟改正,但精度较低,和电离层延迟真值比较,只能改正电离层延迟的50%～60%[1,5];多频改正模型效果好,可用于高精度定位,但该类型接收机成本较高,不适用于低成本定位的应用场合;而全球格网模型相较于区域模型精度仍有提升空间,其中GIM(global ionosphere map)的预报产品c1pg、c2pg的精度为2～4 TECU(1 TECU= 1 × 1016个电子/m2)[6];区域电离层模型中,常见的有三角级数模型和多项式模型,且三角级数模型的建模精度一般比多项式模型的精度高[7-9]。

A2i+N2+N3+NI+NJsin (ih)),

(1)

(2)

人工神经网络(artificial neural network,ANN)是一种模拟生物神经元的算法[10]。利用 ANN对电离层延迟建模,可以发挥其非线性建模的优势,在提高电离层延迟改正精度方面有较大的潜力。目前,常见的ANN主要分为前馈神经网络(feedforward neural network,FNN)[11]、卷积神经网络(convolutional neural network,CNN)[12]和递归神经网络(recurrent neural network,RNN)[13]。而ConvLSTM[14]兼顾了CNN和RNN的优点,可以有效地对长时间段的空间序列进行学习,适用于电离层区域建模。

对于全球格网模型,文献[15]～[16]采用了传统的FNN对电离层进行建模,RMSE最高可以达到5 TECU;对于区域格网模型,文献[17]～[20]采用RNN进行建模, RMSE最高为3.48 TECU,王松寒利用BP神经网络-多项式融合模型得到的平均绝对误差约为0.20 TECU[9]。这些基于ANN的电离层延迟模型有以下缺点:全球模型的预测VTEC的时间分辨率和空间分辨率不高,格网点之间的经差、纬差较大,预测间隔较长;区域模型多是针对某个坐标位置的模型,缺乏对整个区域进行VTEC预测的研究,且使用的ANN提取时空规律的能力较弱。

因此,本文从上述两点出发,基于电离层延迟改正理论和北京市GNSS连续运行观测站(continuously operating reference station,CORS)的观测数据,确定ConvLSTM模型的超参数,给出合适的网络结构,建立北京及周边地区的区域电离层延迟模型,并对此模型的VTEC预测精度进行分析。

1 ConvLSTM模型原理

图1展示了ConvLSTM单元内部的数据流动。

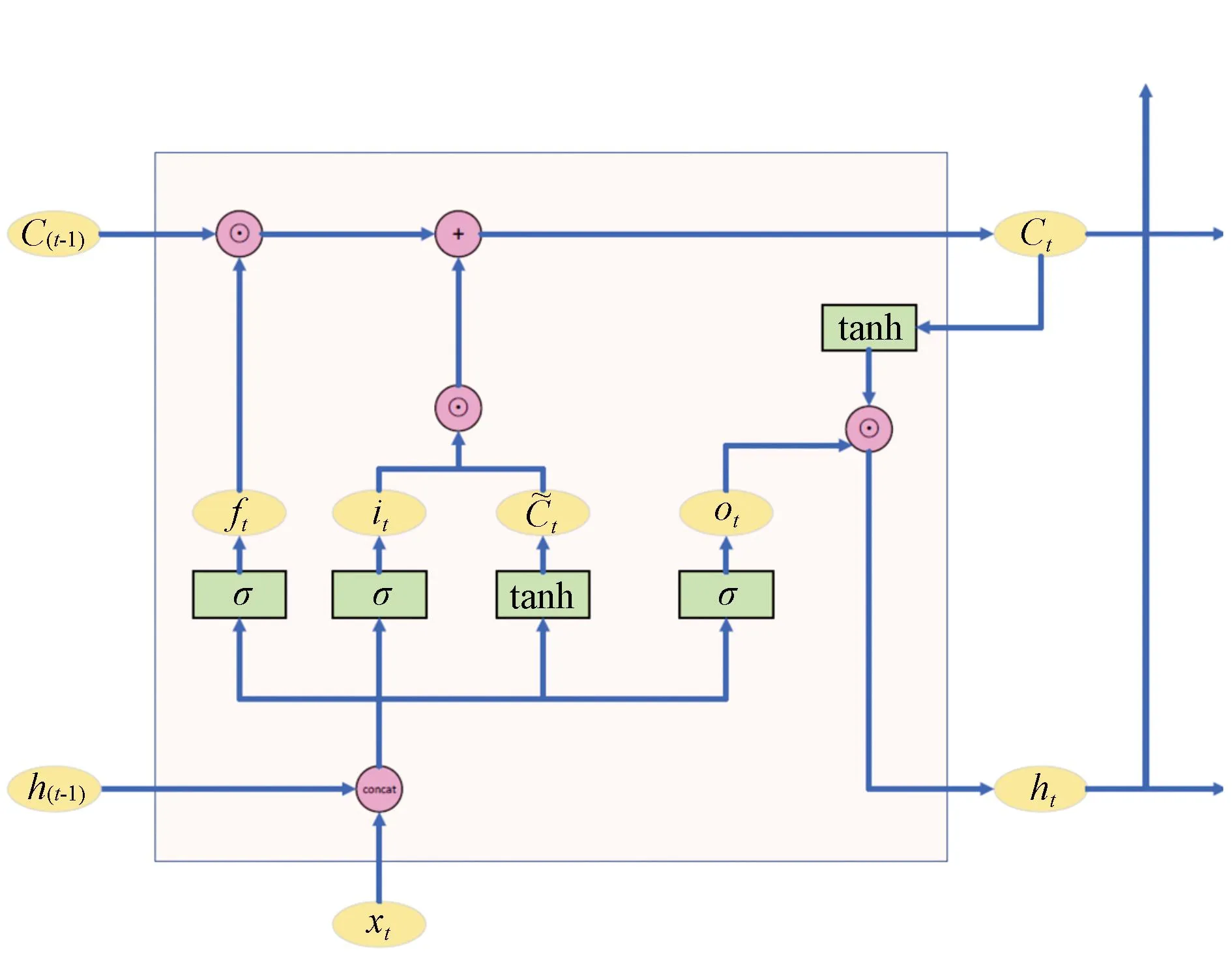
图1 ConvLSTM 单元

(3)

(4)

ConvLSTM的算式如下:

ft=σ(Wxf*xt+Whf*ht-1+bf),

(5)

it=σ(Wxi*xt+Whi*ht-1+bi),

(6)

(7)

(8)

ot=σ(Wxo*xt+Who*ht-1+bo),

(9)

ht=ot⊙tanh (Ct).

(10)

其中,*代表卷积运算,⊙代表哈达玛乘积。

2 数据和模型

2.1 实验设计

已有数据:2016-09-15—2016-10-14的北京13个CORS站观测值、太阳黑子数、太阳辐射通量F10.7、地磁Ap指数。

实验步骤:①选择输入到ConvLSTM模型中的数据;②确定ConvLSTM模型的超参数;③得到VTEC预报值;④精度分析。

2.2 选择模型的输入数据

电离层延迟是复杂的参数,与时间、空间位置、太阳活动、地磁活动等因素有关[21-22],所以输入ConvLSTM 模型的数据拟从以下5类中选择:

1)历史VTEC信息。原始数据来自于北京市的13个CORS站,其中,BJFS站为IGS站,其余12个站属于北京本地的CORS网,时间范围是2016—2020年,见表1。

表1 北京CORS站

13个站分布在39.61°～40.93°N,115.71°～117.17°E。同时,可以确定北京中心点大致位于(40°N,116.5°E)。

利用北京GNSS CORS站的观测数据,计算出位于31°～47°N,108°～124°E 区域(网格大小0.5°×0.5°,共33行33列的格网点)的VTEC值,作为电离层延迟建模的主要输入信息;同时考虑到北京中心点位于13个CORS站中间, 其VTEC计算值精度更高,因此让北京中心点VTEC值也成为一个输入。

2)地方时。一般而言,VTEC随地方时变化明显。VTEC在白天变化剧烈,14时左右达到峰值;在凌晨和夜间变化平缓,VTEC值较小,如图2所示。因此,地方时是影响 VTEC预测的重要因素。

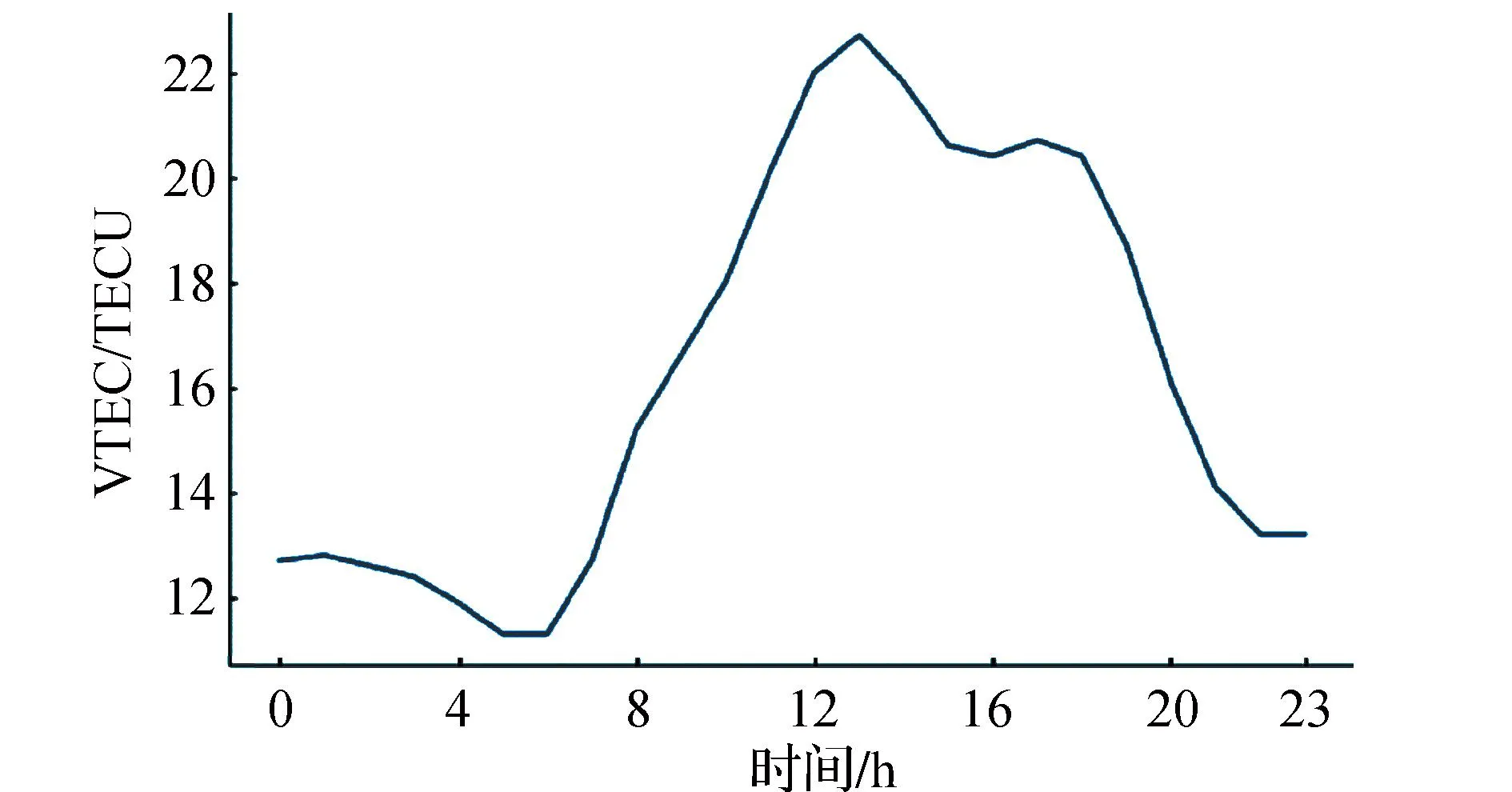
图2 北京中心点VTEC(2016-09-15)

3)经度和纬度。一般而言,纬度比经度更能影响VTEC值——低纬度的地区接受的太阳辐射更多,因此会有较高的VTEC,见图3。同时,VTEC受高程的影响较小。所以,经纬度是影响VTEC预测的重要因素。但由于本文建模的区域是固定的,所以不必输入坐标信息。

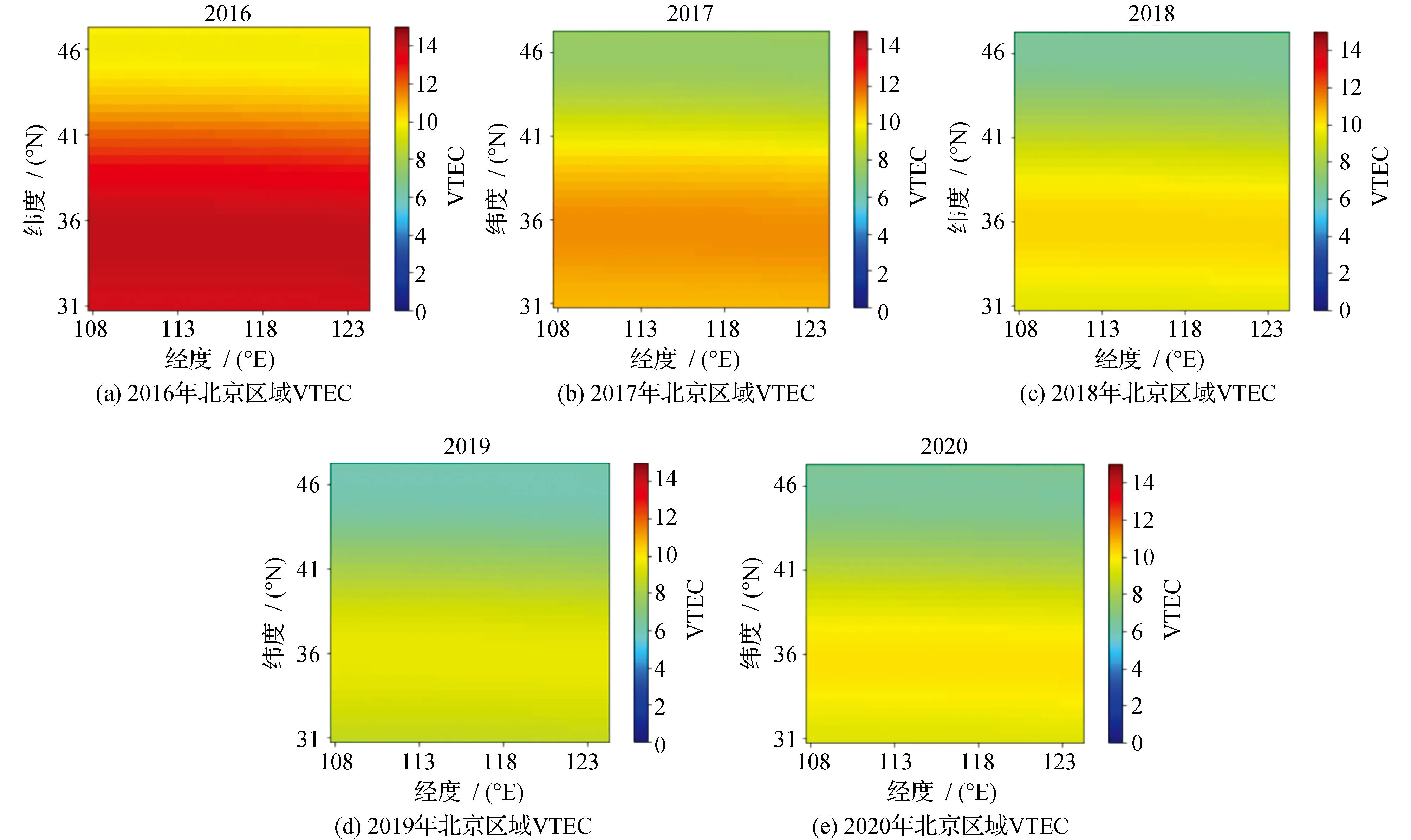
图3 北京及周边区域 VTEC(2016—2020年)

4)太阳活动参数。导致电离层电离的主要原因,就是其接收了大量的太阳辐射。通常用太阳辐射通量F10.7和太阳黑子数来反映太阳活动强度。F10.7与太阳黑子数的数据来源于美国太空天气预报中心,如图4所示。但在太阳活动较弱的时期,太阳黑子数常常为0,不能合理地反映太阳活动强度,也不能反映电离层的变化情况;VTEC 与太阳辐射通量F10.7的相关性分析如表2、图5所示,时间范围为2016—2020年,可见,在最好情况下,VTEC与太阳辐射通量F10.7的Pearson 相关系数也只有0.595,呈弱相关。因此,ConvLSTM 模型输入不应包含F10.7与太阳黑子数。

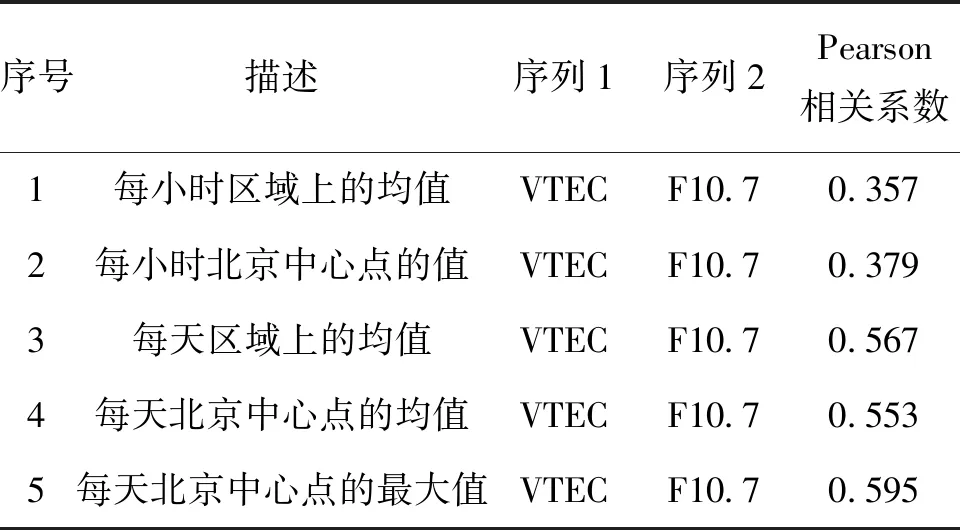
表2 VTEC与太阳辐射通量F10.7的相关性分析

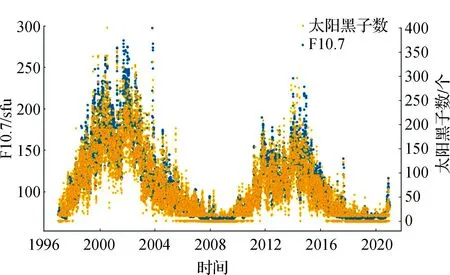
图4 太阳黑子数和太阳辐射通量F10.7(1996—2020年)

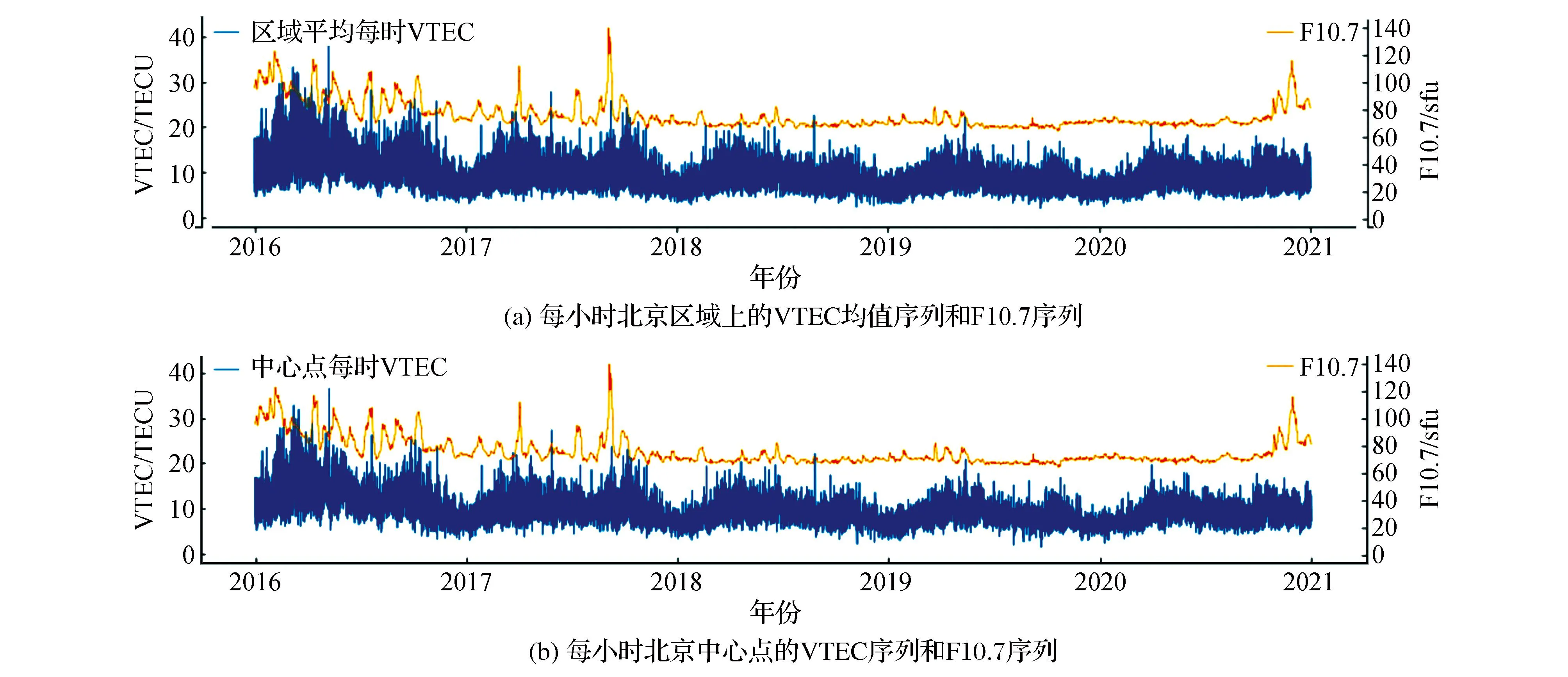
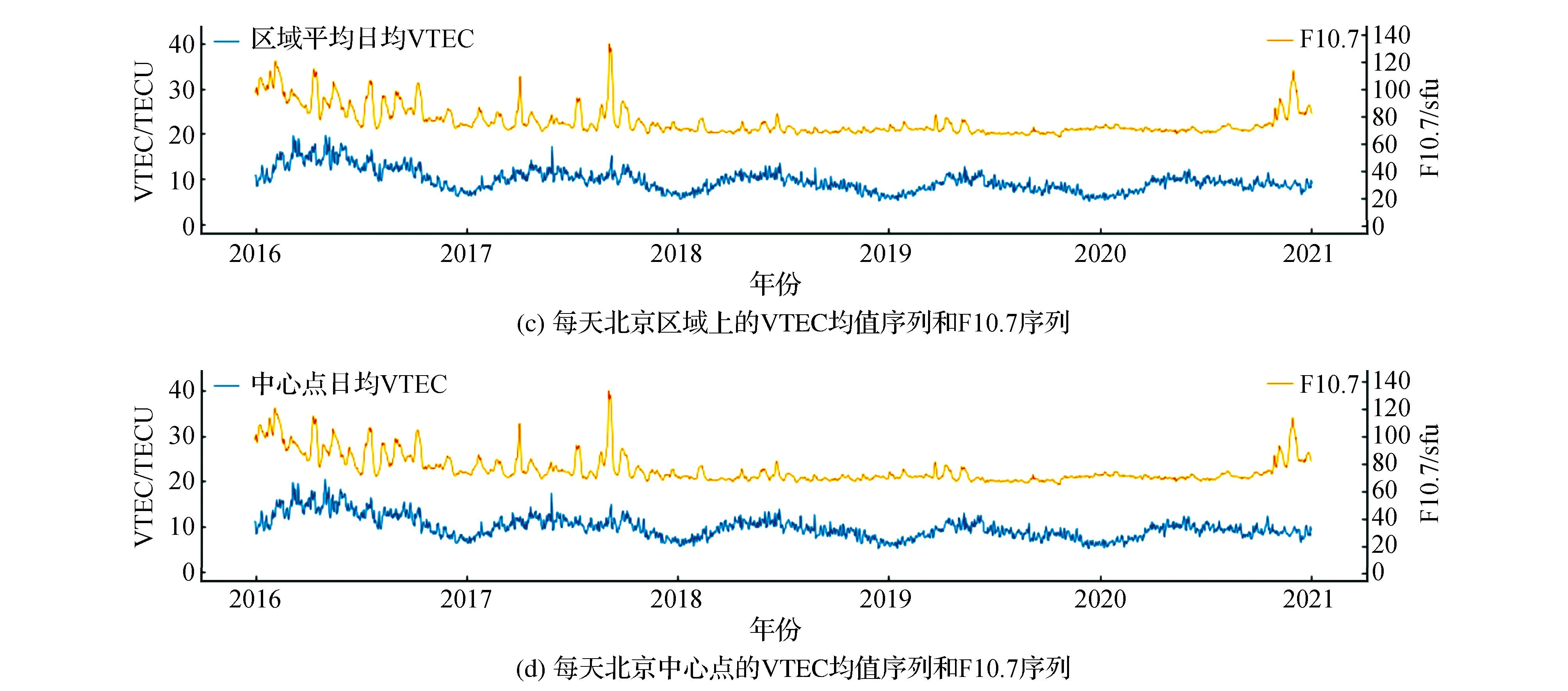
图5 VTEC 和 F10.7 走势对比

5)地磁活动参数。地球磁层扰动会影响电离层VTEC,本文用Ap指数来表征地磁活动,Ap指数越大,说明地磁活动越强。采用英国大地测量局提供的地磁Ap指数与VTEC进行相关性分析,结果如表3、图6所示,时间范围为2016—2020年。可见,在最好情况下,VTEC与地磁Ap指数的Pearson相关系数也只有0.391,呈弱相关。因此,ConvLSTM 模型输入不应包含地磁Ap指数。

表3 VTEC与地磁Ap指数的相关性分析

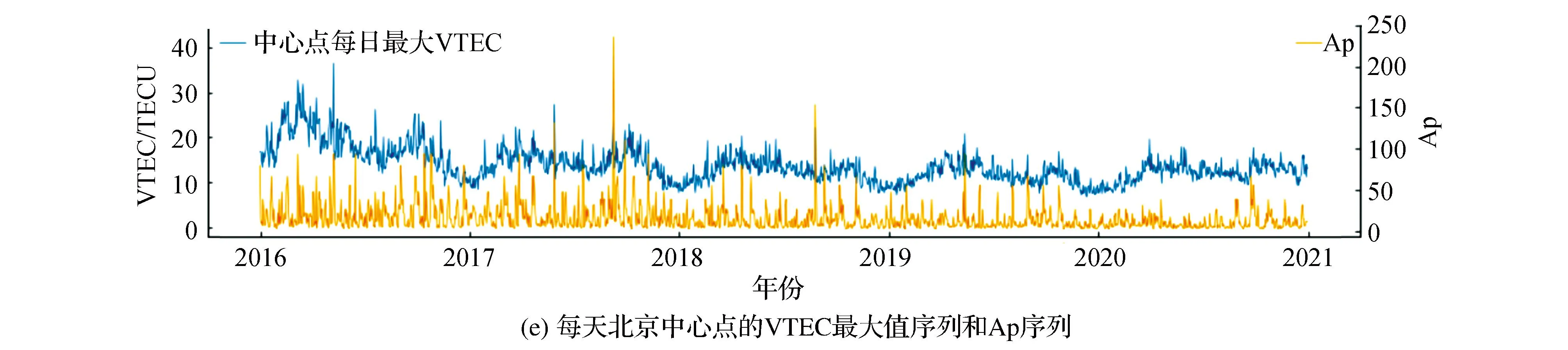
图6 VTEC和Ap走势对比

最终确定以下3种ConvLSTM的输入数据,见表4。

表4 ConvLSTM输入数据

2.3 基于ConvLSTM建立电离层延迟模型

建立模型涉及到深度学习,文中使用的深度学习框架为Pytorch。为方便叙述,将文中搭建的模型称为VclNet。VclNet为短期预报模型,由7 d的数据预测1 d的VTEC。根据对数据类型分析和预训练,确定VclNet模型的各项参数,如表5所示。

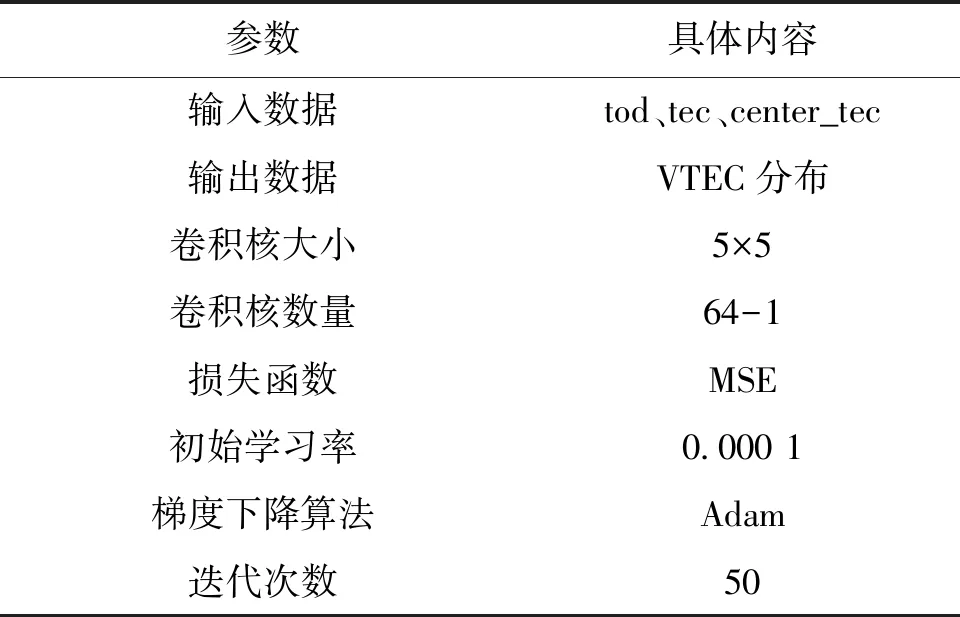
表5 VclNet模型参数

2.4 获取其他模型的预报数据

GIM产品c1pg、c2pg从IGS官网下载得到,Klobuchar预报数据由其模型计算得到。多项式模型和三角级数模型预报数据则是由前一天的VTEC数据建模并预测后一天得到。且多项式模型的参数n=3,m=3;三角级数模型的N2=NI=NJ=1,N3=0,N4=6。

3 实验总结与分析

3.1 VclNet模型VTEC预报精度分析

文中利用训练好的VclNet模型得到了2016-09-15—2016-10-14共30 d的北京及周边区域的VTEC预报值,并将其与同时段的GIM产品c1pg、c2pg,三角级数模型,多项式模型和Klobuchar模型的预报结果作对比,分析这6种预报值的精度。

3.1.1 单点VTEC预报值精度分析

因为由Bernese5.2计算得到的北京中心点VTEC受边界影响较小,也更准确,因此将其作为参考值,画出4种预报结果的误差,得到图7。

图7 北京中心点VTEC预报误差(2016-09-15—2016-10-14)

图8描述了GIM产品、Klobuchar模型和VclNet模型在此段时间预报的北京中心点VTEC值误差的分布,表6列出了精度指标具体计算结果,包括平均误差μ、标准差σSTD、平均绝对误差σMAE、均方根误差σRMSE。由此可知:①三角级数模型、GIM产品的预报结果与VclNet模型的预报结果相近,其中,c2pg比c1pg的预报效果更好;②多项式模型和Klobuchar模型预报效果较差,其中,Klobuchar模型预报值的σRMSE最大,平均误差μ最大,标准差σSTD最大;③VclNet模型的预报值的σRMSE最小,为1.99 TECU,精度最高,平均误差μ约为0,标准差σSTD较小。

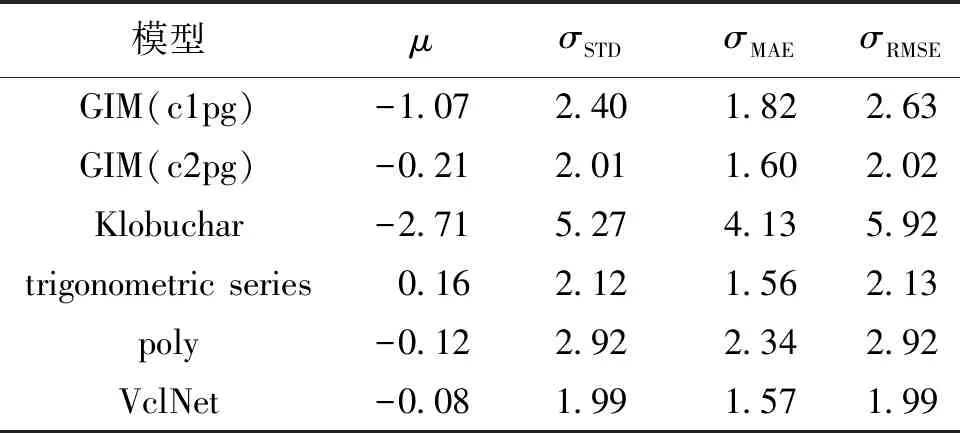
表6 北京中心点VTEC预报值精度分析

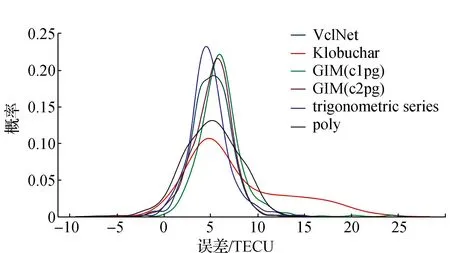
图8 北京中心点VTEC预报误差分布(2016-09-15—2016-10-14)

3.1.2 区域VTEC预报值精度分析

各模型在区域(31°～47°N,108°～124°E)的VTEC预报值的精度分析见表7。可见,各模型的区域VTEC预报值的误差和中心点的情况类似,即VclNet的预报精度最高,其σRMSE为2.09 TECU。同时,除了三角级数模型和多项式模型的μ指标,其他区域预报的各精度指标都比中心点的大。

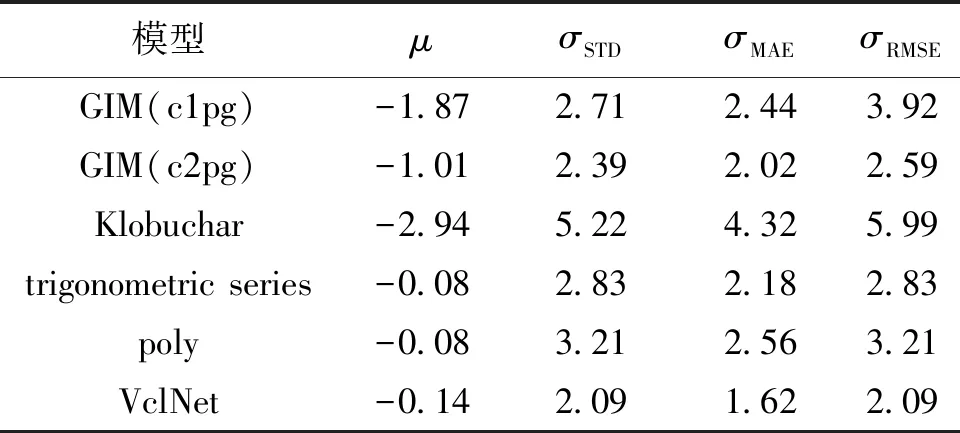
表7 北京及周边区域VTEC预报值精度分析

3.2 实验结论

文中利用Bernese5.2计算得到位于31°～47°N,108°～124°E 的区域的VTEC,并获取了31°～47°N,108°～124°E的GIM(c1pg)、GIM(c2pg)、Klobuchar的VTEC 预报值、VclNet的VTEC预报值,时间跨度为2016-09-15—2016-10-14。根据对上述预报值的精度分析,可知:对于每个模型,中心点VTEC预报值的表现比区域的更好;6种模型中,VclNet的预报效果最好,其对北京中心点VTEC预报值精度为1.99 TECU,区域VTEC预报值精度为2.09 TECU,Klobuchar模型的预报效果最差,中心点精度和区域精度分别为5.92 TECU和5.99 TECU。根据表7,区域预报精度由高到低的模型/产品依次是VclNet模型、GIM(c2pg)产品、三角级数模型、多项式模型、GIM(c1pg)产品、Klobuchar模型。

4 结束语

由于缺乏低成本高精度的电离层延迟模型,本文尝试利用北京区域的地方时、历史VTEC信息建立基于ConvLSTM的VclNet模型,并对GIM产品、Klobuchar模型、VclNet模型的预报结果进行比较:VclNet精度最好,单点预测精度、区域预测精度分别为1.99 TECU、2.09 TECU;GIM产品次之,c2pg的精度为2.02 TECU和2.59 TECU,c1pg的精度为2.63 TECU和3.29 TECU;三角级数模型的精度和GIM的c2pg相近,精度为2.13 TECU和2.83 TECU;多项式模型的精度较低,为2.92 TECU和3.21 TECU;Klobuchar模型较差,其精度为5.92 TECU和5.99 TECU。

文中只对基于ConvLSTM的区域电离层延迟建模作了初步的研究,还可以在以下几个方面进行进一步的研究和探讨:①太阳辐射通量F10.7、地磁Ap 指数和VTEC的关系还有待研究。在文中算例中,F10.7、Ap与VTEC的相关性较低,因此并不能通过F10.7和Ap 预测VTEC,其原因可能和该地区所在纬度有关系。②对VTEC均值和方差的预报还有待研究。由于输入VclNet的是标准化后的数据,模型只能提取数据的相对关系;且由于F10.7和Ap指数与VTEC的相关性很低,所以无法通过太阳活动和地磁活动来预测区域内VTEC的均值和方差。因此,文中目前采用的是移动平均的方法。