多路绝对激光测距仪精密三维控制网的建立与解算

黄 赫,范百兴,段童虎,陈 哲,邹方星

(信息工程大学,郑州 450001)

现代工业的飞速发展对大尺寸精密测量技术的测量精度、测量范围、测量效率等要求越来越高[1-5]。而全局测量对整体测量的性能和适用性起决定作用,是控制精密测量精度的基础[6],故建立高精度的控制网在粒子加速器准直及预准直阶段磁铁定位[7-9]、飞机零部件装配定位[10-11]、大型望远镜定位校准[12-13]等工程及装备制造领域十分必要。以高能同步辐射光源(high energy photon source,HEPS)储存环预准直单元实验研究项目的磁铁高精度定位需求为背景和出发点,其预准直阶段中优于±30 μm磁铁定位精度要求点位测量精度优于±10 μm,要使点位测量精度达到该需求就必须要求控制网的平均点位精度优于±5 μm,而如今以全站仪、激光跟踪仪为主体建立的控制网很难满足这一精度需求。目前激光测距类仪器测距精度最高可达±0.3 μm/m,远高于测角精度(目前最高可达±0.5″),仅通过测距建立精密三维测边控制网,无需引入角度测量,可以避免角度测量所带来的误差,具有很高的理论精度。

目前,使用激光跟踪仪建立高精度控制网是大尺寸全局测量精密控制的有效手段。由于激光跟踪仪测距精度远高于测角精度,近年来,许多学者在激光多边法精密测量方面进行了大量研究[14-20],取得了较为可观的研究进展。

多路绝对激光测距仪在0.2～30 m的测量范围内可直接测量点间距离,其测距不确定度小于±0.5 μm/m且最高可达±0.3 μm/m;可实现准直器与目标反射镜之间的绝对测距[21-22],如图1所示。该仪器具有测量精度高、操作方便、直接量距等优点,突破了现有的测距模式和精密三维控制网的布网方法。

图1 准直器与反射镜间绝对测距

本文基于多路绝对激光测距仪高精度的绝对测距性能,测量所有控制点间的距离,利用高精度的测距值建立精密三维测边控制网,并建立了对应的仅含控制点间距离的秩亏自由网平差模型。在平差之前,利用改进的LM(levenberg-marquardt)算法解超定非线性方程组迭代求解的方法,在未知数任意取值的前提下实现坐标概算;并选用数量及布局不同的控制点设计了三维测边网的建网方案,对照方案,在整体范围为8 m×3.5 m×2.5 m的大理石标定场进行了实验,建立了高精度的三维测边控制网,最后通过坐标反算距离与原始测距数据对比,验证了控制网精度的可靠性。

1 仅含控制点间距离的三维测边网平差模型

如图2所示,设三维测边控制网中共有n个相互通视的控制点,用多路绝对激光测距仪测量第i(i=1,2,…,n)个控制点与第j(j=1,2,…,n且j≠i)个控制点之间的测距值为Sij(1≤i≤n,1≤j≤n,i≠j),则得到式(1)所示的n(n-1)个观测方程:

图2 多路绝对激光跟踪干涉仪建立三维测边网

图3 LM算法迭代求解流程

(i≠j).

(1)

对观测方程式(1)线性化,可得到如式(2)所示的n(n-1)个误差方程:

(2)

式(2)中的自由项为:

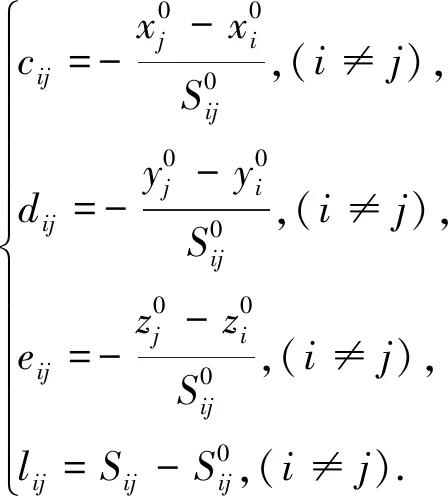
(3)

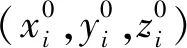
(i≠j).

(4)

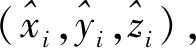
若使整个控制网可解,观测方程个数应大于等于未知参数个数,即n(n-1)≥3n,进一步可得n≥4,故控制点不得少于4个且可以相互通视观测。

2 随机初值的控制网坐标概算

控制网进行平差解算前,需得到所有未知参数的近似值,而近似值的选取会直接影响平差结果[24-25]。若近似值选取不当,即如果控制点间相对位置关系与实际关系存在质的差异,整个三维测边控制网就无法得到正确的平差解。因此完成三维测边控制网的坐标概算是一项十分重要的工作。

目前,多台或多站位激光跟踪仪建立的三维测边网以高效率、高精度等优势被广泛使用,其坐标概算是基于激光跟踪仪的极坐标定位原理,通常以测站1坐标系为概算坐标系,直接测量控制点的坐标作为平差所需坐标近似值[26]。而多路绝对激光测距仪不含坐标测量功能,引入多种仪器联合测量势必会大大减弱建网的便捷性。

式(1)所列方程组,方程数远大于未知数,属于超定方程组。故可以将坐标概算转化为超定方程组求解问题。本文采用改进的LM算法迭代求解非线性超定方程组,通过随机取一组初值X0∈Rn实现坐标概算。

2.1 观测方程组

当n满足n≥4的解算条件时,根据式(1)可建立含n(n-1)个观测方程的超定方程组F(x1,y1,z1,…,xn,yn,zn)=0,如下所示:

(5)

2.2 改进的LM算法迭代求解非线性超定方程组

超定方程组F(x1,y1,z1,…,xn,yn,zn)=0记为F(X)=0,该方程组由观测方程组成,故式(5)至少存在一组满足条件的非空解集X*。

牛顿迭代法是一种非线性方程组的有效解法,其通过计算每次迭代所使用的搜索方向,即牛顿步,进行迭代求收敛解[27]。但牛顿步的计算需要非奇异的雅各比矩阵,而超定方程组的雅各比矩阵属于奇异阵,故牛顿法在求解该超定方程组时不再适用[28]。

Levenberg和Marquardt提出的LM算法有效解决了雅各比矩阵属于奇异阵的问题。本文在LM算法基础上,基于信赖域技术,通过修改迭代参数,得到了一种能有效求解非线性方程组的改进的LM算法。算法改进后具有超线性收敛性,故可通过随机取初值X0迭代求解,进而应用在解决三维测边网坐标概算的问题上。

应用改进的LM法可以解决超定非线性方程组的雅各比矩阵不可逆的问题,通过式(6)计算每次迭代的搜索方向,即每次迭代的试探步,记第k次迭代的试探步为dk,并通过式(8)判断是否接受dk,进而迭代得到收敛解。

(6)

式中:F(Xk)为方程组F在第k次迭代解集Xk处的值,Jk为F(X)在X=Xk处的雅各比矩阵,λk为迭代参数,I为单位阵。

λk的选取对使用LM算法得到非线性方程组的收敛解至关重要。本文选取λk为:

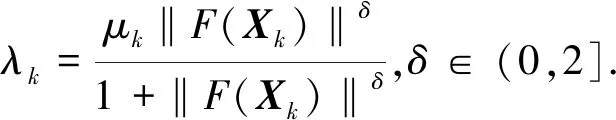
(7)

由式(7)可知,在迭代求解过程中,如果在k次迭代中,当Xk远离X*时,||F(Xk)||较大,||F(Xk)||δ/(1+||F(Xk)||δ)趋近于1,此时λk≈μk;当Xk接近X*时,||F(Xk)||趋近0,此时λk≈μk||F(Xk)||δ,因此可以将随机值赋予初始值集X0。

联合式(6)和式(7)即可计算出第k次迭代求解集的试探步dk,根据式(8)判断是否采用试探步对解集进行改正。

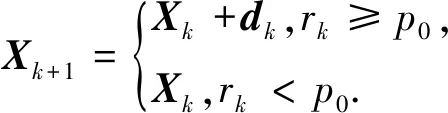
(8)

如式(8)所示,是否接受试探步dk,主要由比率rk的值决定。

对于rk的求解,本文定义价值函数ψ(X)= ||F(X)||2,以及该函数在第k次迭代中的预测变化量(Predk)及实际变化量(Aredk)为:

(9)

则有:

(10)

同时,利用rk对迭代中μk做出判定如下:

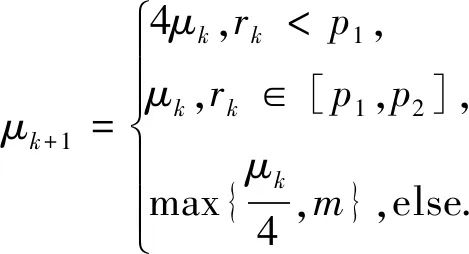
(11)

迭代求X*的步骤见图 3。

2.3 坐标概算有效性验证

(12)

3 三维测边网平差解算及精度评定

当控制点个数满足n≥4条件时,式(2)的误差方程可以写成矩阵形式:

(13)

其中:

因多路绝对激光测距仪测量的是控制点间的距离,故不存在i=j的观测方程及误差方程,故A为n(n-1)×3n的矩阵。

(14)

由于空间三维测边网缺少必要的起算数据,造成了系数矩阵A的秩亏,故A为秩亏阵,进而求解所得的法方程矩阵为奇异阵,测边网属于秩亏网,本文采用秩亏自由网附加重心基准约束进行平差解算[29]。

考虑到多路绝对激光测距仪测距误差受测量距离的影响,故应将测距误差随距离的变化考虑在内,采用测距加权的方法定权。设多路绝对激光测距仪的标称测距精度为σl,则从第i个控制点观测第j个控制点的距离值Sij对应的权值为:Pij=(σlSij)-2,可构建权阵为:

(15)

(16)

在误差方程的基础上,增加约束条件:

(17)

(18)

解算的关键是确定约束矩阵G。A秩亏数即缺少的基准个数为d=u-t,其中u为控制点坐标数量,t为必要观测量。在传统的控制网平差中,控制网起算条件包括控制网的位置(一个固定点的三维坐标)、控制网的方向(一个固定方向的三轴余弦值)和一个尺度基准。由于多路绝对激光测距仪测距精度高,尺度基准可由距离观测值确定,缺少的基准个数为6,因此附加约束矩阵G的维数为6[30],即:

(19)

按照最小二乘原理构造目标函数得到法方程如下:

(20)

式(20)左乘GT可得K=0,即法方程可变化为:

(21)

结合式(21)与式(17),可得控制点三维坐标参数及未知参数的权逆阵为:

PXGGTPX)-1.

(22)

(23)

(24)

(25)

4 实例分析

本次实验在中国科学院高能物理研究所恒温实验室内的大理石标定场上进行,大理石标定场的整体空间为8 m×3.5 m×2.5 m,实验全程用一套球形发射器和1.5英寸角隅棱镜(red-ring reflector,RRR)。在大理石标定场的大理石柱上,共选取8个空间位置分布均匀且可以相互通视的控制点,相邻两个控制点间的高差在1.5 m左右,实验场地、控制点布局及三维测边网网形的模型图及实物图如图4所示。

图4 实验场地、控制点布局及三维测边网网形

基于多路绝对激光测距仪测量每个控制点与其余控制点之间的距离(见图5),利用对应的n(n-1)个距离测量值建立三维测边控制网。

图5 控制点间绝对测距

在8个控制点间共测量56个距离观测值,由于存在对向观测且多路绝对激光测距仪标称精度较高,实验中根据同一距离本应相等或差异不大的原则,对存在偶然误差的测距值进行了复测,复测率小于10%。最终得到的经加常数改正的测距原始数据中,同一边长对向观测的差值最大为±3.6 μm,最小小于±0.1 μm,观测值可靠性强。

根据控制点数量及分布的不同,对实测的56条边长观测值进行分组分析,共有如下5种方案:

方案1,选取P3、P4、P5、P64个控制点间共12个距离观测值建网;

方案2,选取P2、P3、P4、P5、P65个控制点间共20个距离观测值建网;

方案3,选取P1、P2、P3、P6、P7、P86个控制点间共30个距离观测值建网;

方案4,选取P2、P3、P4、P5、P6、P7、P87个控制点间共42个距离观测值建网;

方案5,选取P1、P2、P3、P4、P5、P6、P7、P88个控制点间共56个距离观测值建网。

4.1 未知数随机取值坐标概算

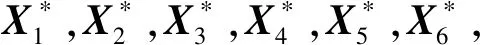
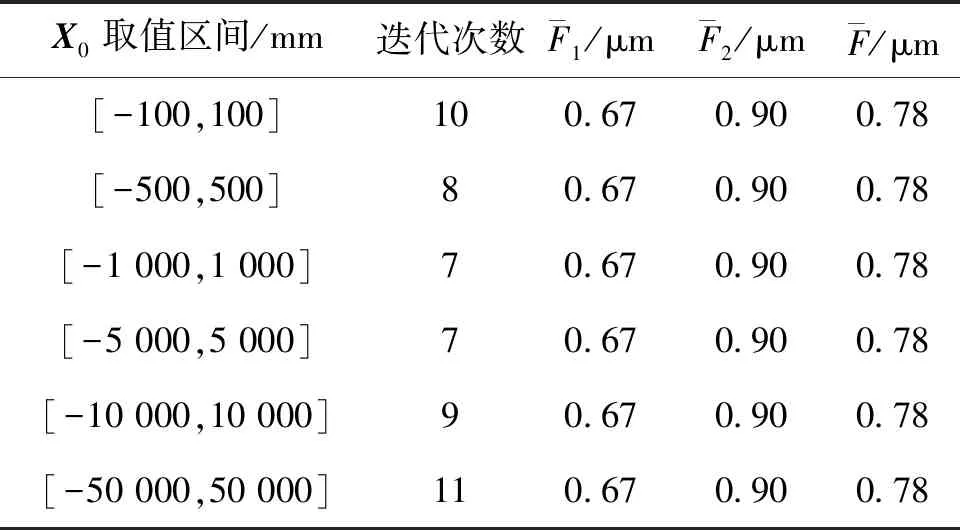
表1 方案1未知数不同取值区间坐标概算结果

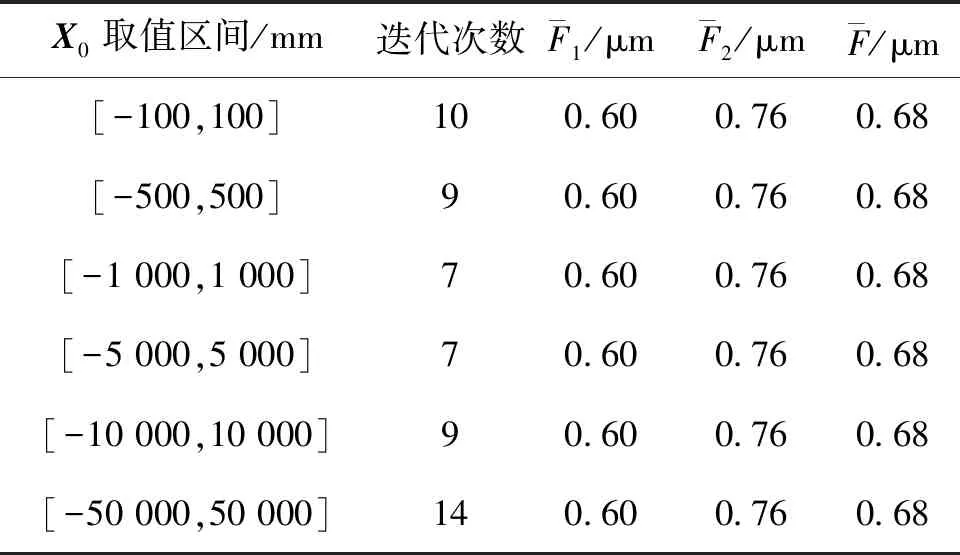
表2 方案2未知数不同取值区间坐标概算结果

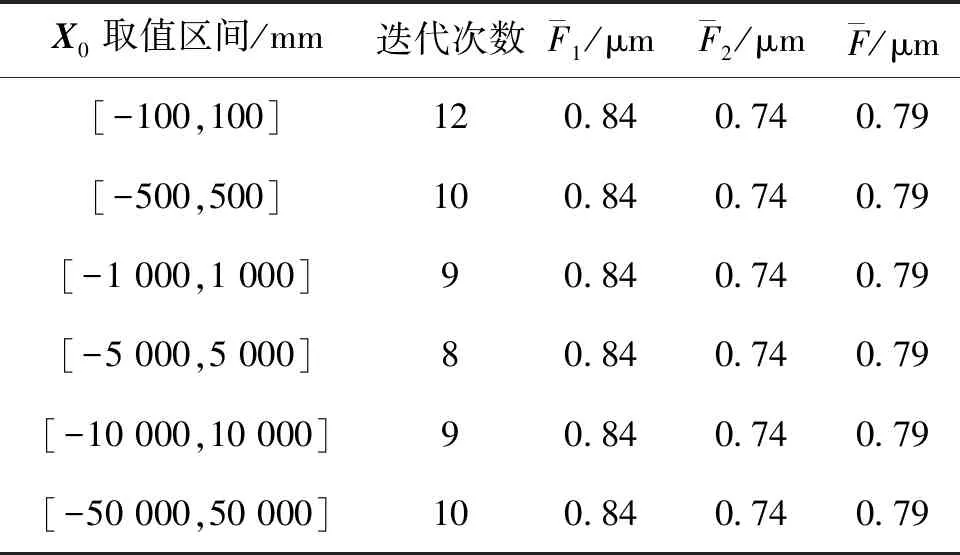
表3 方案3未知数不同取值区间坐标概算结果

表4 方案4未知数不同取值区间坐标概算结果

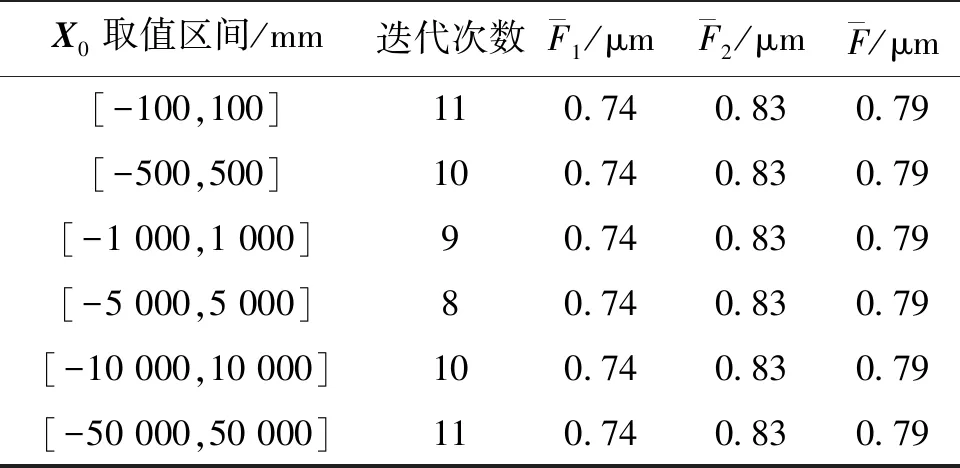
表5 方案5未知数不同取值区间坐标概算结果

通过表1～5分析可得,控制点固定的情况下,利用改进的LM算法进行坐标概算,无论未知数初值在任何区间选取,只会影响迭代的次数,而不会影响解的精度和一致性,说明所有控制点之间的相对位置关系可以固定且精度较高,即解算结果作为平差解算的坐标初始值的有效性强。

4.2 三维测边网平差分析

通过4.1节的分析,验证了对未知数任意取值进行坐标概算方法的可行性,概算所得的三维坐标值精度高、一致性强,可作为三维测边网的坐标初值进行平差。为了验证多路绝对激光测距仪所建三维测边网的精度,结合所建立的秩亏自由网平差模型,对实验数据进行处理,5种方案平差结果见表6和图6。

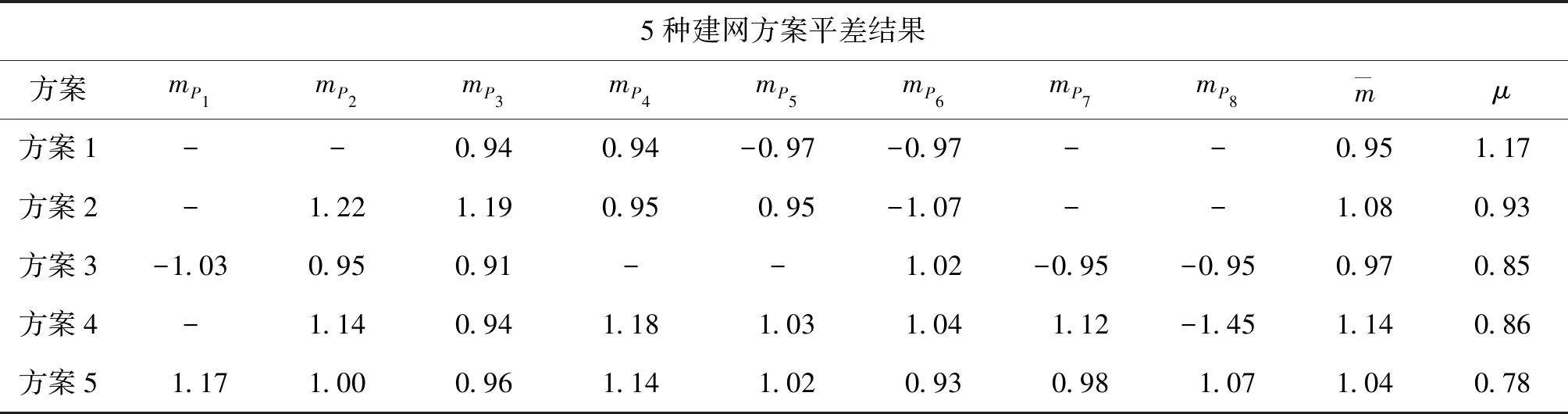
表6 三维测边网平差结果 μm

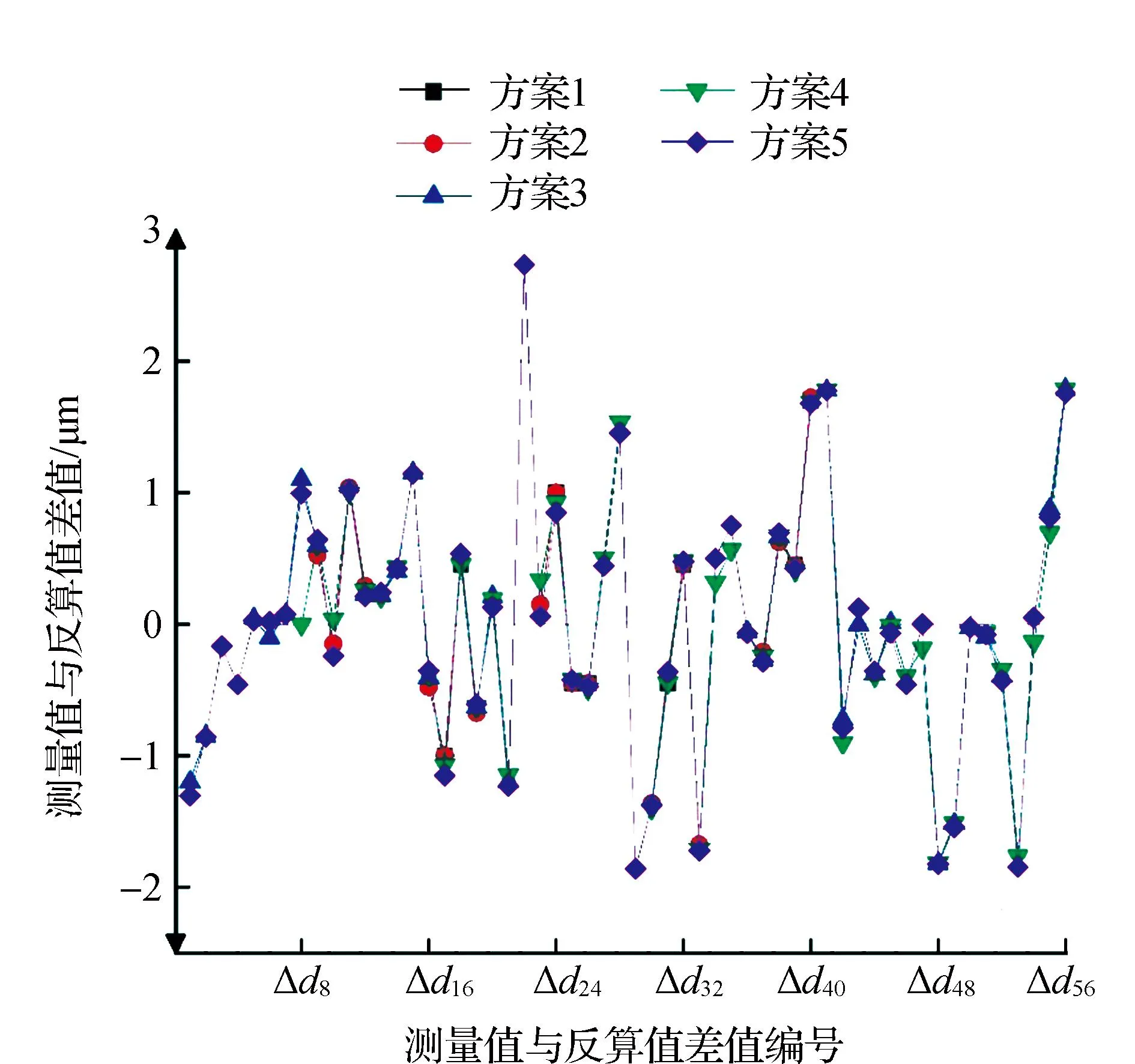
图7 距离反算与原始测距数据差值结果

表6和图 6结果可得,基于多路绝对激光测距仪高精度绝对测距性能,通过双向观测值对比进而复测排除测距偶然误差,可得到准确度及精确度较高的测距值以建立高精度的三维测边网。同时,对5种不同方案得到的控制点精度进一步对比分析可得,在所选控制点高差较大、点位分布较均匀、通视条件好的基础上,控制点数量对点位精度的影响较小,三维测边控制网的控制点的平均点位精度优于±1.14 μm,满足HPES预准直阶段磁铁定位对控制网精度的需求。

4.3 距离反算精度验证

为了验证所建立的三维测边控制网的精度可靠性,利用平差解算所得坐标对两点间距离进行反算,并与经加常数改正后的原始测量值进行对比。为了记录方便,对测距值进行编号,56个边长测量值为SP1P2～SP8P7,设与其对应反算值的差值为Δd1～Δd56。经计算,5种方案中,距离测量值与反算值差值绝对值最大为2.732 6 μm,最小为0.001 5 μm,结果如图 7所示。

由图 7及计算数据分析可得,方案1所建控制网采用的12条边长中,距离观测值与反算值差值的绝对值在0～0.5 μm、0.5～1 μm、1～2 μm、大于2 μm,分别占测量数的50%、33.3%、16.7%、0%;方案2采用的20条边长中,占比分别为55%、20%、25%、0%;方案3采用的30条边长中,占比分别为53.3%、20%、26.7%、0%;方案4采用的42条边长中,占比分别为52.4%、21.4%、26.2%、0%;方案5采用的56条边长中,占比分别为51.8%、19.6%、26.8%、1.79%。可见,仅利用测距值进行坐标概算和秩亏自由网平差后,得到的控制点的平均点位精度优于±1.14 μm,可靠性强。

5 结束语

本文对基于多路绝对激光测距仪建立精密三维测边控制网进行了实验研究,完成了以下工作:

1)根据多组范围不同的随机初值选取,采用改进的LM算法对未知数进行迭代计算,得到了高稳定性和高精度的概算结果,实现了任意初值的坐标概算。

2)建立了仅含控制点间距离的秩亏自由网平差模型,基于该仪器的测距特性及标称精度,设计了控制点数量不同的5种建网方案,在恒温间内整体范围为8 m×3.5 m×2.5 m的大理石标定场上,采集了不同方案的距离数据;利用对应的秩亏自由网平差模型进行解算,建立了控制点数量不同的高精度三维测边网。通过对5种不同方案得到的控制点精度进一步对比分析可得,在实验环境及选点合理的基础上,通过排除测距偶然误差得到高精度的测距值,可建立控制点平均点位精度优于±1.14 μm、点位精度最优可达±0.55 μm的三维测边控制网,且控制点数量在4～8个范围内时,控制点数量增多对建网所得控制点的精度影响较小。在实际工程应用上,为了能在多路绝对激光测距仪测距范围内建立该精度的控制网,控制点的选取应满足高差尽可能大、稳定性好、通视效果好、点位分布均匀等条件。

3)通过平差结果坐标反算控制点间距离与实测原始数据对比,两者差值的绝对值几乎均在2 μm以内,最小为0.0015 μm,其中优于0.5 μm的边长数超过建网所用边长数的一半。故基于该仪器该方法建立的平均点位精度优于±1.14 μm,且点位精度最优可达±0.55 μm的三维测边网精度具有可靠性。

研究结果满足实验要求,在粒子加速器预准直阶段、大型飞机部件数字化对接装配、高精度坐标测量、天线位姿测量、固体火箭发动机推力线测量等现代工业应用方面具有实用价值。