大气阻力摄动对低轨微纳卫星轨道影响建模及仿真

杨志强 王应鹏 魏欣欣

DOI：10.19850/j.cnki.2096-4706.2024.01.021

收稿日期：2023-05-25

摘  要：微纳卫星的轨道位置对其在轨运行和任务执行的稳定性至关重要，长期受到大气阻力加速度摄动的影响导致卫星轨道的重要参数逐渐衰减。为了深入研究这种影响，通过分析微纳卫星在大气层中受到的阻力加速度与卫星的迎风面积、质量以及大气阻力系数之间的关系，建立了一种可靠的大气阻力摄动影响模型。采用经典的轨道六根数来描述微纳卫星的轨道位置，并运用四阶龙格库塔方法对相应的微分方程进行求解。通过对大气阻力摄动对低轨微纳卫星轨道具体影响的建模和仿真分析，为研究人员制定有效的卫星轨道控制策略提供了重要的参考依据。

关键词：微纳卫星；轨道；大气阻力摄动；轨道六根数；仿真

中图分类号：TP391.9  文献标识码：A  文章编号：2096-4706（2024）01-0104-05

Modeling and Simulation of the Influence of Atmospheric Drag Perturbation on the Orbit of Low Earth Orbit Micro-nano Satellite

YANG Zhiqiang， WANG Yingpeng， WEI Xinxin

（School of Information Engineering， North China University of Water Resources and Electric Power， Zhengzhou  450045， China）

Abstract： The orbital position of micro-nano satellites is crucial for their stability in orbit operation and task execution. The long term influence from atmospheric drag and acceleration perturbations leads to the gradual attenuation of important parameters in satellite orbit. In order to investigate this impact in depth， a reliable atmospheric drag perturbation model is established by analyzing the relationship among the drag acceleration of micro-nano satellites in the atmosphere and the windward area， mass， and atmospheric drag coefficient of the satellite. The classical six orbital elements are used to describe the orbital position of micro-nano satellites， and the fourth order Runge-Kutta method is used to solve the corresponding differential equations. The modeling and simulation analysis of the specific impact of atmospheric drag perturbation on the orbit of low orbit micro-nano satellites provide important reference for researchers to develop effective satellite orbit control strategies.

Keywords： micro-nano satellite; track; atmospheric drag perturbation; six orbital elements; simulation

0  引  言

微纳卫星是指质量小于100千克、具有实际功能的卫星[1]。随着高新技术的不断发展和需求的推动，微纳卫星正逐渐展现出其独特的优势。这些卫星具有体积小、功耗低、开发周期短等特点，能够以更低的成本完成复杂的空间任务。因此，微纳卫星在科研、国防和商业等领域发挥着重要的作用。它们为我们提供了一种高效且经济的解决方案，推动了空间技术的进步和应用的广泛发展[2]。在过去的二十多年里，微纳卫星经历了迅速而显著的发展，如今已经成为航天器研制领域的重要趋势之一。其革新性的技术和特点对全球科技和经济产生了巨大的影响，标志着当前空间技术发展的新潮流。微纳卫星的迅速发展将继续推动航天技术的进步，为未来的航天事业开辟更加广阔的前景[3]。

微纳卫星长期在轨运行会受到各种摄动的影响，由于微纳卫星为低轨，因此受到的最为主要的摄动加速度为地球非球形摄动和大气阻力摄动[4]。靳旭红、黄飞[5]等人通过基于自由分子流试验粒子Monte Carlo方法，并嵌入多种国际主流大气模型，对超低地球轨道卫星的大气阻力进行了有效预测和分析。具体以GOCE卫星为研究对象，计算并分析了该卫星的大气阻力特性。高兴龙、李志辉[6]等人针对大型航天器在气动力和力矩分量的基础上，建立了航天器轨道-姿态动力学摄动模型，对大型航天器短期轨道衰降变化进行了仿真预测。King-Hele[7]等人推导了近地点距离和轨道周期在卫星寿命期间如何随离心率变化，以及离心率如何与时间相关的方程。对于低轨微纳卫星而言，现有的摄动力模型不能完全满足要求，其主要原因是模型中参数误差较大。刘涵月[8]对空间目标大气阻力系数以及轨道预报等内容进行研究，为提高低轨空间目标轨道预报精度，提出了一種基于随机森林的大气阻力系数确定方法。通过选取两颗位于不同轨道高度的卫星进行仿真实验，实验结果表明随机森林估计的CD可明显改善轨道预报精度。Hasan[9]等人对大气阻力对低轨道卫星在不同面积质量比下的影响进行了建模和仿真，仿真结果表明随着面积质量比的增大，所有轨道要素的大气阻力效应都有所增加。刘劲宏、徐劲[10]等人针对火箭体和大型航天器的大气再入问题，并实现更高精度的大气再入预报，引入了基于雷诺数的大气阻力模型。通过对微分方程进行数值积分确定适当的大气阻力系数，从而获得准确的预报结果。余进江、陈俊宇[11]等人提出了一种基于长短期记忆神经网络（LSTM）的热层大气密度经验模型校正方法。该方法利用NRLMSISE-00模型计算的密度、太阳活动指数和地磁活动指数作为基础输入，并利用CHAMP卫星加速度计反演的密度数据来训练NRLMSISE-00模型的误差模型。这种方法能够提高校正后的大气密度模型的精度，为大气密度预测和航天器轨道计算等应用提供更准确的结果。实验结果表明，经过校正后的大气密度模型精度显著提高。Nwankwo[12]等人探究了大气阻力对低轨卫星轨道要素的影响，并验证了大气阻力对低轨卫星在轨运动具有重要的影响。

本文建立了大气密度随高度变化的计算模型、大气阻力摄动下微纳卫星轨道位置计算模型，通过对仿真结果的分析，可以为研究人员制定有效的卫星轨道控制策略提供重要参考，从而确保微纳卫星能够持续稳定地执行在轨任务。

1  基础模型建立

1.1  轨道计算模型

为了准确描述航天器的位置，我们需要引入一个参考坐标系。在本文中，我们选择了轨道坐标系OXYZ作为参考坐标系。该坐标系的原点位于微纳卫星的质心，OZ轴指向地心，OX轴指向卫星在轨道平面上的运动方向，并且与OZ轴垂直。通过右手坐标系的约定，我们可以确定OY轴的方向，从而完全确定了该坐标系。图1为该坐标系的示意图。

根据传统的方法，图2为本文使用经典的轨道六根数（半长轴a，偏心率e，轨道倾角i，升交点赤经Ω，近地点幅角ω，真近点角f）来计算微纳卫星的轨道位置。

半长轴a：半长轴确定了椭圆轨道的长半轴长度，即轨道的大小。同时，这个根数也决定了发射卫星到这个轨道需要多少能量，因为根据活力公式，一个确定轨道的机械能是固定的。

偏心率e：轨道偏心率表示轨道偏心程度，类似于椭圆的扁率。当偏心率近似等于0时，轨道被称为近圆轨道，此时地球的质心几乎与轨道的几何中心重合。而当偏心率大于0且小于1时，轨道呈现椭圆形状，偏心率越大，轨道越扁。

轨道倾角i：轨道倾角是指轨道平面与赤道平面之间的夹角，用于描述轨道的倾斜程度。它可以简单地表示轨道平面是水平的、垂直的还是倾斜的。卫星轨道的倾角决定了卫星在地球上的覆盖范围，并对发射场和运载火箭的能力产生重要影响。不同的倾角将对发射和轨道安排提出不同的要求，因此倾角成为发射任务中的一个重要参数。

升交点赤经Ω：为了理解轨道根数中的升交点赤经Ω，我们需要在称为惯性系的三维空间中进行。在航天动力学中，常常使用J2000坐标系作为惯性系。J2000坐标系的原点位于地球质心，参考平面是J2000平赤道面，其中Z轴指向平赤道面北极，X轴指向J2000平春分点，而Y轴与X和Z轴构成了直角右手系。

近地点幅角ω：表示卫星从升交点出发到达近地点在轨道平面内所经过的角度，它反映了轨道的朝向。

真近点角f：这是一个时变根数，用来描述某一个确定时刻卫星在轨道中所处的位置，是地心指向卫星和指向近地点矢量之间的夹角。

卫星距地心距离r的计算：

（1）

轨道高度计算：

（2）

式中Re表示地球半径，采用地球的平均半径Re = 6 371 km。

真近点角f的可以确定卫星在轨的位置，真近点角f的微分方程如下：

（3）

该微分方程可以通过四阶龙格-库塔（Runge-Kutta）方法进行数值求解，从而可以计算出卫星距地心的距离r和轨道高度h。

卫星轨道周期计算：

（4）

式中μ表示地球引力常数，μ = 398 600 km3/s2。

1.2  大气阻力摄动模型

1.2.1  大气密度计算模型

高层大气密度与多种不同的参数都有关系，最为明显的就是随着高度的增加而减小。根据流体静力学可构建“一维大气密度模型”，即地心距r处的大气密度为：

（5）

式中，ρ0表示参考球面r = r0上的大气密度；H表示密度标高，该值会随着大地高度的升高而升高。

由于大气密度随着高度的变化越到高层越慢，因此密度标高H是一个变化量，且随着高度的增加而缓慢变大。当高度在200～600 km时，H的变化可以简化为：

（6）

式中H0对应r = r0时的密度标高；μ≈0.1。

卫星近地点高度计算公式为：

（7）

1.2.2  静止大气摄动

如果假设大气为静止的，则大气的运动速度为零，微纳卫星相对于大气的运动速度等于卫星本身的速度，与卫星的运动速度相等。由此，可以得到大气阻力摄动加速的形式为：

（8）

CD为大气阻力系数，一般的取值为1.5～3.0；s/m为卫星迎风面积与质量的比值，一般卫星的面积与质量比在2～20（m2/t）；ρ为大气密度。

将式（8）带入到轨道坐标系（OXYZ）下的高斯型摄动方程，可得到在大气阻力摄动影响下的高斯型摄动方程：

（9）

式中n表示平均角速度，平均角速度计算公式：

（10）

2  仿真结果及分析

微纳卫星在轨运动受大气阻力摄动的建模仿真中，采用了如表1所示的轨道六根数作为模型参数。

微纳卫星在轨道上所受到的大气阻力加速度与卫星的迎风面积、质量以及大气阻力系数密切相关。表2列出了与卫星构型相关的参数以及大气阻力系数。

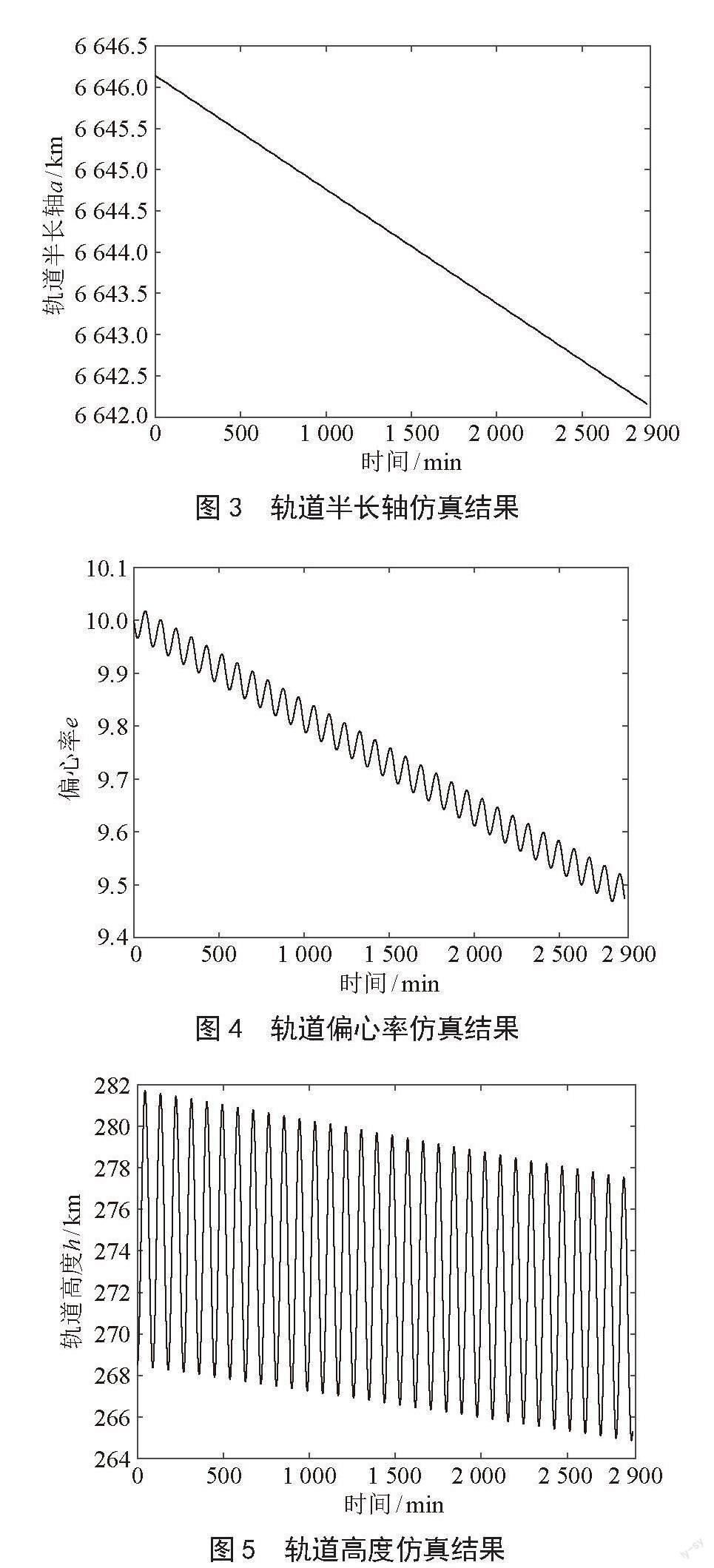
根据微纳卫星的轨道大气摄动模型，選取了上述参考值作为主要参数进行了仿真研究。在仿真过程中，采用了每60秒为间隔的仿真时间步长，并且总共仿真了2 900分钟，相当于约32个轨道周期。仿真结果如图3、图4和图5所示。

图3为微纳卫星轨道半长轴的仿真结果，从图中可以观察到随着时间的推移，轨道半长轴逐渐下降。这是由于大气阻力摄动对微纳卫星施加减速作用导致的结果。卫星受到大气层的阻力，使其失去动能，进而使轨道半长轴逐渐减小。

图4为微纳卫星轨道偏心率的仿真结果，从图中可以观察到偏心率在大气阻力摄动的影响下周期性下降。大气阻力的作用导致卫星的速度减小，从而使卫星轨道逐渐变得更加圆形，即偏心率减小。

图5为微纳卫星轨道高度的仿真结果，从图中可以看出，在大气阻力摄动的影响下，轨道高度呈现周期性下降的特征。这是因为大气阻力对卫星施加的减速作用会导致卫星的轨道高度逐渐降低。然而，由于大气密度的变化和轨道偏心率的影响，轨道高度的下降呈现出周期性变化的模式。

1）大气阻力摄动还会引起轨道半长轴的衰减。轨道半长轴是描述轨道大小的参数，衰减意味着卫星的轨道逐渐向地球靠拢。这会导致卫星的运行高度逐渐降低，可能会影响其与地面站的通信质量、遥感观测的准确性以及其他任务的执行能力。

2）大气阻力摄动会导致轨道偏心率的不断衰减。偏心率是描述轨道椭圆程度的参数，其衰减意味着轨道椭圆趋向于圆形。这会影响卫星的轨道形状和大小，进而对卫星的运动轨迹和相对位置产生影响。如果偏心率衰减过快或超出设计范围，卫星可能无法满足任务要求，例如与目标进行精确交会或保持特定轨道间隔。

3）随着轨道高度的衰减，卫星与地球表面的距离逐渐减小。这增加了卫星与大气层的相互作用，使其更容易受到空气摩擦力和热负荷的影响。这可能导致卫星的轨道稳定性下降，增加了对姿态控制和热管理系统的要求，同时也可能缩短卫星的使用寿命。

3  结  论

仿真结果表明，微纳卫星长期在轨运行中受到大气阻力摄动的影响会导致轨道偏心率、轨道半长轴和轨道高度的衰减，若不加以控制，大气阻力摄动将对微纳卫星的轨道参数产生不可忽视的影响，这将直接影响卫星在轨任务是否能顺利完成和卫星的安全性。这也需要考虑在设计和运行阶段采取适当的措施，如轨道修正、能源管理和姿态控制策略，以确保卫星能够持续稳定地执行任务并保持运行安全性。

仿真结果展示了微纳卫星轨道半长轴、轨道高度和偏心率在大气阻力摄动影响下的变化。这些变化对于卫星轨道控制、任务规划和卫星寿命的评估具有重要意义，研究人员可以根据这些结果进一步优化卫星设计和制定相应的控制策略，以确保卫星的稳定运行和任务执行的有效性。

参考文献：

[1] 陆震.小卫星和微纳卫星应用现状与挑战 [J].兵器装备工程学报，2018，39（6）：1-7.

[2] 郭鑫，施思寒，付伟达，等.微纳InSAR卫星总体技术研究 [J].宇航总体技术，2022，6（2）：17-24.

[3] 张伟，彭攀，沈朱泉，等.精致微纳卫星设计与实践 [J].航天器工程，2018，27（6）：19-26.

[4] 王世航.超低轨航天器轨道维持与星下点轨迹控制研究 [D].哈尔滨：哈尔滨工业大学，2021.

[5] 靳旭红，黄飞，程晓丽，等.超低地球轨道卫星大气阻力预测与影响因素分析 [J].清华大学学报：自然科学版，2020，60（3）：219-226.

[6] 高兴龙，李志辉，陈钦，等.大型航天器无控飞行再入时间短期预报的轨道摄动方法研究 [J].载人航天，2020，26（5）：566-573.

[7] KING-HELE D G，WALKER D M C. The contraction of satellite orbits under the influence of air drag，III. High-eccentricity orbits （0？ 2≤ e<1） [J].Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences，1962，267（1331）：541-557.

[8] 刘涵月.基于随机森林的低轨空间目标大气阻力系数确定研究 [D].武汉：武汉大学，2021.

[9] HASAN N O，ZAKI W H A，IZZET A K. The Effect of Atmospheric Drag Force on the Elements of Low Earth Orbital Satellites at Minimum Solar Activity [J].NeuroQuantology，2021，19（9）：24-37.

[10] 劉劲宏，徐劲，杜建丽，等.基于雷诺数的大气阻力模型在飞行器再入预报中的应用 [J].空间科学学报，2022，42（2）：277-283.

[11] 余进江，陈俊宇，桑吉章.基于LSTM神经网络的热层大气密度模型校正 [J].测绘地理信息，2022，47（5）：37-41.

[12] NWANKWO V U J，DENIG W，AJAKAIYE M P，et al. Simulation of atmospheric drag effect on low Earth orbit satellites during intervals of perturbed and quiet geomagnetic conditions in the magnetosphere-ionosphere system [C]//2020 International Conference in Mathematics，Computer Engineering and Computer Science （ICMCECS）.Ayobo：IEEE，2020：1-7.

作者简介：杨志强（1999—），男，汉族，河南鹤壁人，硕士研究生在读，主要研究方向：系统建模与仿真；王应鹏（1997—），男，汉族，河南洛阳人，硕士研究生在读，主要研究方向：系统建模与仿真；魏欣欣（1998—），女，汉族，河南安阳人，硕士研究生在读，主要研究方向：系统建模与仿真。