开采沉陷动态预测时间函数参数变化规律研究
——以Weibull 为例
2024-04-13喻成林张宏贞范洪冬
喻成林 ,张宏贞 ,范洪冬
(1.徐州市自然资源和规划局,江苏 徐州 221008;2.中国矿业大学 环境与测绘学院,江苏 徐州 221116)
地下资源开采后,破坏其原有平衡状态,经过覆岩传递到地表,是1 个复杂的动态移动过程,涉及地质、采矿、空间等多方面因素,许多学者在开采沉陷动态变形原理、模型、精度等方面进行了研究,并取得了大量成果。开采沉陷动态预测模型主要有动态力学模型和时间函数模型2 类,目前主要采用时间函数构建开采沉陷的动态变形过程;常用的时间函数有Knothe 时间函数模型、双曲线时间函数模型、Gompertz 时间函数模型、logistic 曲线时间函数模型及 Weibull 曲线时间函数模型等。
王悦汉等[1]将动态移动过程分为顶板初次垮落前、顶板垮落未充满采空区、顶板垮落已充满采空区、表土移动4 个阶段,采动岩体分为连续介质、拟连续介质、非连续介质3 种介质,分阶段建立了动态力学预测模型;吴侃等[2]提出了基于时间序列分析的动态预测模型;崔希民等[3]建立基于Knothe 时间函数的概率积分预计方法,根据临界开采尺寸确定时间影响系数;张兵等[4-5]建立了1 种新的优化分段Knothe 时间函数,并提出了基于实测数据的反算时间函数对比求参法、基于概率积分参数的直接计算法的2 种优化分段Knothe 时间函数参数求取方法;刘玉成等[6-7]分析了下沉动态过程的Knothe 时间函数模型的不足,提出了幂指数的Knothe 时间函数,分析了常见地表沉陷时间函数模型的下沉、下沉速度、下沉加速度与时间关系,认为Weibull 曲线时间函数模型能完整地描述地表沉陷的动态过程;孙闯等[8]建立了考虑松散层下沉特点的双因素Knothe 时间函数;王军保等[9]借鉴岩石流变力学中非定常流变模型,构建了变时间影响系数的Knothe 的地表动态沉陷预测模型;许国胜等[10]回归分析得到地表动态移动变形参数与地质及开采技术参数之间的关系;李春意等[11-12]进行了基于Logistic 时间函数、正态分布时间函数的动态沉陷预测;张永胜等[13]提出了以地表点最大下沉速度时刻为分界点,结合偏差改正、生长函数模型的1 种分段Weibull时间函数;刘东海[14]根据常村观测资料,指出Weibull 时间函数参数不固定,两参数变化规律为距边界变化类偏态分布;JAROSZ 等[15]考虑开采产生的空间收敛,建立了双参数Sroka-Schober 时间函数;KOWALSKI[16]在Knothe 和Sroka-Schober双参数时间函数基础上,提出了广义时间函数;González Nicieza 等[17]在Knothe 时间函数基础上,引入正态分布函数,建立了正态分布时间函数。
综上,总体认为地表动态下沉量与时间的关系曲线呈“S”形曲线,下沉速度为0→Vmax→0 过程,下沉加速度为0→+amax→-amax→0 过程。
1 地表动态移动过程覆岩变化特征
工作面上方的覆岩及地表在井下资源开采后,经历弯曲、垮落、再次压缩等过程,但在工作面不同位置的岩层完整厚度、位移、受力等经历过程不同,根据工作面回采、覆岩受力与垮落情况,将工作面回采结束后的地表分为3 个部分,工作面动态分析分区图如图1。

图1 工作面动态分析分区图Fig.1 Partition diagram of dynamic analysis of working face
1)竖向整体受压区(Ⅰ区)。处于工作面外侧煤柱区域,工作面开采边界至开采影响边界之间。此部分区域在整个回采期间,覆岩经历了弯曲,但没有垮落、再次压缩等过程,在竖向上是完整的。在整个开采期间竖向方向整体是受压状态。
2)中间区(Ⅱ区)。处于工作面内测靠近煤柱区域,工作面开采边界至覆岩动态完全区边界(覆岩垮落角确定边界与工作面开采边界之间)。此部分区域在整个回采期间,覆岩经历了弯曲、垮落、非完全再次压缩过程等部分或全部过程,主要是由于岩梁的存在导致垮落非充分及垮落岩石受力非充分,在竖向上部分破裂,且离工作面边界(煤柱)越远,破裂高度越大,即完整覆岩厚度减小。在整个回采期间主要经历如下几个阶段:①受到影响到工作面推到下方前,在竖直方向上整体是受到压缩变形,竖向受力增大;②推过后至覆岩垮落前,在竖直方向上整体是受到拉伸变形、竖向受力减小;③垮落后至移动稳定,在竖直方向上整体是受到压缩变形,竖向受力增大至稳定。垮落岩石部分再次受到压缩变形。
3)动态完全区(Ⅲ区)。处于工作面内测远离煤柱区域,覆岩动态完全区(覆岩垮落角确定边界至采空区中心)。此部分区域在整个回采期间,覆岩经历了弯曲、垮落、完整再次压缩过程,在竖向上部分破裂,破裂高度一致。在整个回采期间主要经历如下几个阶段:①受到影响到工作面推到下方(垮落前),在竖直方向上整体是受到压缩变形,竖向受力增大;②到再次受到压缩前,在竖直方向上整体是受到拉伸变形,竖向受力减小;③到移动稳定,在竖直方向上整体是受到压缩变形,竖向受力增大至稳定。
根据开采沉陷岩梁相关理论,地表下沉可简化为各种类型岩梁弯曲,其弯曲下沉值与刚度(弹性模量与惯性矩之积)成反比,其中惯性矩与岩梁高度的三次方成正比。结合图1,在同种情况下,上覆岩层刚度、惯性矩变化规律为:Ⅰ区(整体一致,最大)>Ⅱ区(与离开切眼距离成反比)>Ⅲ区(整体一致,最小)。
目前以时间函数为基础的各种地表动态沉陷预测模型参数主要包括:最大变形值、时间函数(时间函数不同,其参数不同),各类参数与覆岩、开采等因素有关,体现其差异,但目前时间函数都采用相同参数,即在工作面不同位置(煤柱内外)的时间函数参数都一样,这与处在工作面不同位置的受力过程、变形过程、岩层破坏情况及岩石力学性质等明显不符。
2 Weibull 时间函数参数变化特点
Weibull 时间函数f(t)数学表达式为:
式中:k、m为参数,正数;t为时间。
据此建立开采沉陷过程中地表下沉时间函数、下沉速度时间函数、下沉加速度时间函数,开采沉陷动态下沉过程曲线如图2。
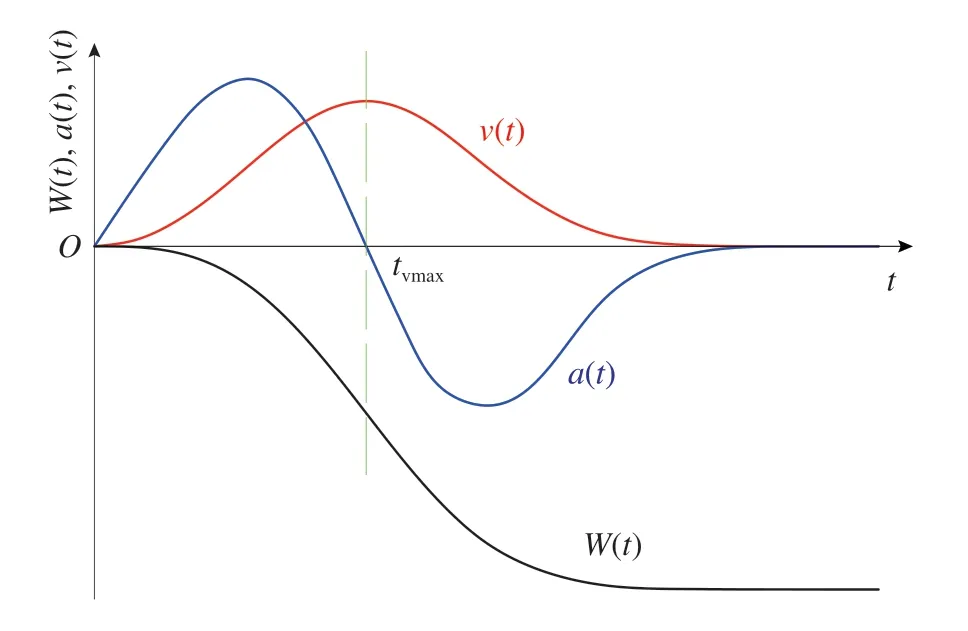
图2 Weibull 时间函数下沉、速度、加速度变化图Fig.2 Weibull time function subsidence, velocity and acceleration variation diagram
式中:W0为该点下沉的最终值。
下沉速度时间函数v(t):
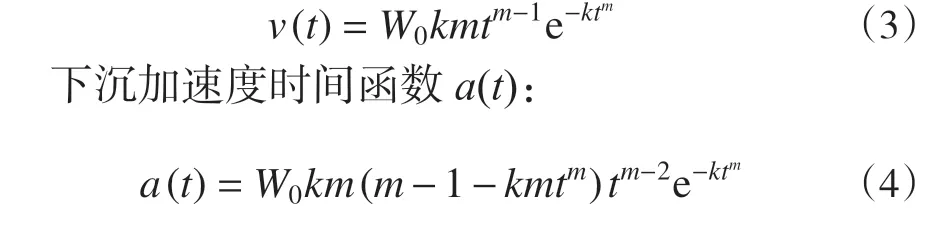
根据前面分析可知:工作面不同位置在回采期间,其覆岩移动、破坏、受力、岩梁刚度等不同,则其动态时间函数参数应不同,m、k决定了Weibull 时间函数的形态变化过程,因此m、k在工作面不同位置其存在差异,以垮落区边界为原点、指向煤柱方向为正,根据前述岩梁弯曲特征简述及相关岩石力学理论,建立其与地面点距离垮落区域边界距离S的函数,工作面不同位置m、k变化情况图如图3。

图3 工作面不同位置m、k 变化情况图Fig.3 Changes of m and k at different positions of working face
在煤柱侧区域(Ⅰ区)m、k为:
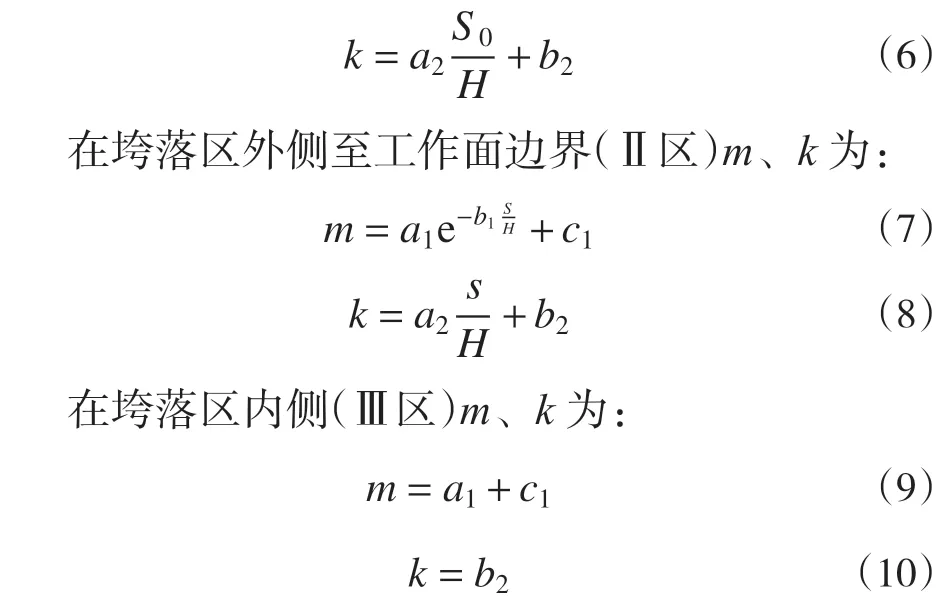
式中:a1、b1、c1、a2、b2为系数;S0为煤柱边界距离;H为工作面采高。
从m、k计算公式及图3 中可以看出:
1)在垮落区外侧为负指数关系,以工作面边界为界,此区域分为2 部分;Ⅰ区(煤柱范围)m变化较小,基本为常数;Ⅱ区(中间区)m变化较大,在垮落区内侧,m为一常数。
2)以工作面边界、垮落区边界为界,此区域分为3 部分;Ⅰ区(煤柱范围)k为常数;Ⅱ区(中间区)m为线性变化;在垮落区内侧,k为一常数。
由于不同位置上覆岩层经历的受力、破坏、变形过程不同,根据开采沉陷相关研究,可采用如下方法确定垮落范围d。① 方法1:采用覆岩力学理论,根据岩梁的相关破裂理论确定垮落边界;② 方法2:采用概率积分法拐点偏移距;③ 方法3:采用顶板覆岩垮落角φ确定,d=H/tan φ。
3 案例分析
某工作面采用长壁一次性采全高采煤法回采。走向为774 m,倾斜宽为220.7 m。工作面开采深度为470~515 m。根据走向观测数据,采用上面的计算模型,获得的反演模型系数见表1。

表1 反演模型系数Table 1 Coefficients of inversion model
根据工作面开采情况,以工作面内侧90 m 为垮落边界,以此确定各点距离边界的S值,根据表1 反演动态时间函数 φ(t)如下:

根据工作面开采情况及参数确定情况,分别以开采结束后实测结果作为最终值、概率积分法预测值作为最终值,进行开采第523 d 的动态预测,实测结果、概率积分法预测值作为最终值的动态预测与实测对比如图4(图中距离以工作面边界为原点,采空区方向为正)。
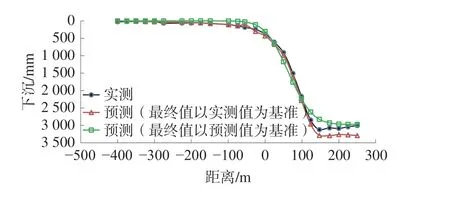
图4 拟合与实测对比图(523 d)Fig.4 Comparison between fitting and actual measurement (523 d)
以实测结果作为最终值:动态预测中误差为110 mm,为最大下沉值的3.5%;以概率积分法预测结果作为最终值:动态预测中误差为130 mm,为最大下沉值的4.2%。
4 结 语
1)分析了工作面上方不同位置的覆岩在开采过程中在竖向上的受力、变形、破坏等变化过程,根据煤柱、垮落情况将覆岩与地表划分为竖向整体受压区、中间区、动态完全区3 个区域。
2)以Weibull 时间函数动态预测模型为例,分析了m、k2 个参数的空间分布规律及特地,构建了2 个参数的分区数学模型及选取准则。
3)分别以实测结果、概率积分法预测结果作为工作面开采结束后的最终值,依据本文动态预测模型及参数确定方法,动态预测中误差分别为110、130 mm,为最大下沉值的3.5%、4.2%,证明本模型的可靠性。
