超前支承压力影响下破碎顶板变形机制与控制

郝英豪 ，王 帅 ，张 鑫 ，王明亮 ，苏海涛

（1.中天合创能源有限责任公司 葫芦素煤矿，内蒙古 鄂尔多斯 017320；2.内蒙古科技大学 矿业与煤炭学院，内蒙古 包头 014010；3.准格尔旗神陶煤炭运销有限责任公司 营沙壕煤矿，内蒙古 鄂尔多斯 010499；4.内蒙古安科安全生产检测检验有限公司，内蒙古 包头 014060）

超前支承压力分布特征及顶板条件对回采巷道超前支护具有重要影响[1-2]，不同围岩条件、覆岩结构下高应力集中区域及围岩变形程度差异性较大[3-4]。掌握超前支承压力分布特征、巷道变形规律及破碎顶板支护方法对维护围岩稳定性具有重要意义[5]。“关键层”理论作为矿山压力及岩层移动的基础性、支撑性成果，广泛应用于矿压显现及超前应力演化等方面[6-7]。超前支承压力分布及影响范围和有无关键层、采煤方法、围岩强度等相关性较大[8-9]。霍丙杰等[10-12]分析了不同覆岩结构条件下位煤层开采应力场环境，探讨了上覆不同尺寸煤柱条件下下位煤层开采应力异常及强矿压现象规律。超前支承压力严重影响顶板完整性[13]，特别是对于顶板自身围岩较破碎情形，破碎顶板下超前支护技术仍处于探索阶段[14]。常见的支护手段主要分为单体液压支柱、超前架组、单体液压支柱+超前架组等[15-16]。单体液压支柱具有支护强度较低、支护效率低及适用性低等特点，常用于局部加强支护或推进速度较缓慢工作面[17]。超前架组则弥补了单体液压支柱的缺点，但对顶板造成不可逆损伤[18]。对于复杂地质条件常常采用两者结合方式，但两者耦合协同作用仍不明确，支护参数选取仍具有一定盲目性[19-20]。目前，针对超前支承压力分布特征影响因素敏感性及破碎顶板超前支护技术与方法研究较少。基于弹性地基梁力学模型，确定了顶板变形影响因素，以数值计算为手段分析了不同埋深、采高、面长对超前支承压力的影响规律，进而提出了破碎顶板注浆加固技术并进行了现场工业性验证。

1 超前段巷道顶板变形特征

1.1 巷道弹性地基梁力学模型

弹性地基梁是顶板底板挠度分析常用的方法[21]。将巷道两帮视为可变形地基，巷道上方顶板视为均布载荷作用下的自由弯曲，根据巷道两侧的对称性建立巷道弹性地基梁力学模型，超前段顶板力学模型如图1。

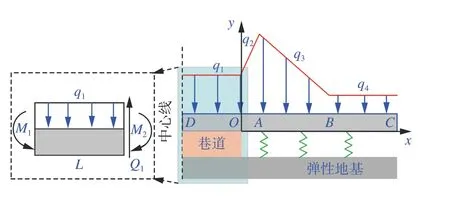
图1 超前段顶板力学模型Fig.1 Mechanical model of super front section roof

根据图1 所示坐标系，DO、OA、AB、BC段的载荷q1、q2、q3、q4分别为：

式中：L1、L2分别为OA、AB段长度，m； ρ、H分别为覆岩平均密度及巷道埋深，kg/m3、m；k1为应力集中系数。

采用截面法可对DO段剪力及弯矩进行求解：

式中：w2为挠度，m；E、I分别为顶板弹性模量和截面惯性矩，GPa、m4；K2为弹性地基系数，N/m3，K2=Eb/(1-v2c)hc；Eb、vc、hc分 别 为两帮弹模、泊松比及厚度，GPa、m。

OA段顶板挠度为：

同理，AB段顶板挠度w3(x)为：

BC段顶板挠度w4(x)为：

由于BC段为半无限梁，可确定C4=D4=0。同时，根据各点转角、弯矩、剪力、挠度连续条件下即变形协调约束，可对待定系数进行求解。

根据挠度与弯矩关系可求出悬梁段上方挠度，即可建立11 个未知数(悬梁段1 个、地基段10 个)的方程，类似梁挠度求解的静定问题，即未知数等于方程数。

式中：θ(x)为转角；M(x)为弯矩；Q(x)为剪力。

本研究旨在分析不同因素对顶板变形的影响，具体参数为：顶板厚度及弹模分别为3.0 m、1.0 GPa，超前应力集中系数为3.0，埋深为400 m。

1.2 顶板弹性模量对顶板变形的影响

巷道顶板抗弯刚度(和弹性模量和惯性矩相关)一定程度上控制挠度变形，不同弹性模量条件下顶板挠度分布特征如图2。

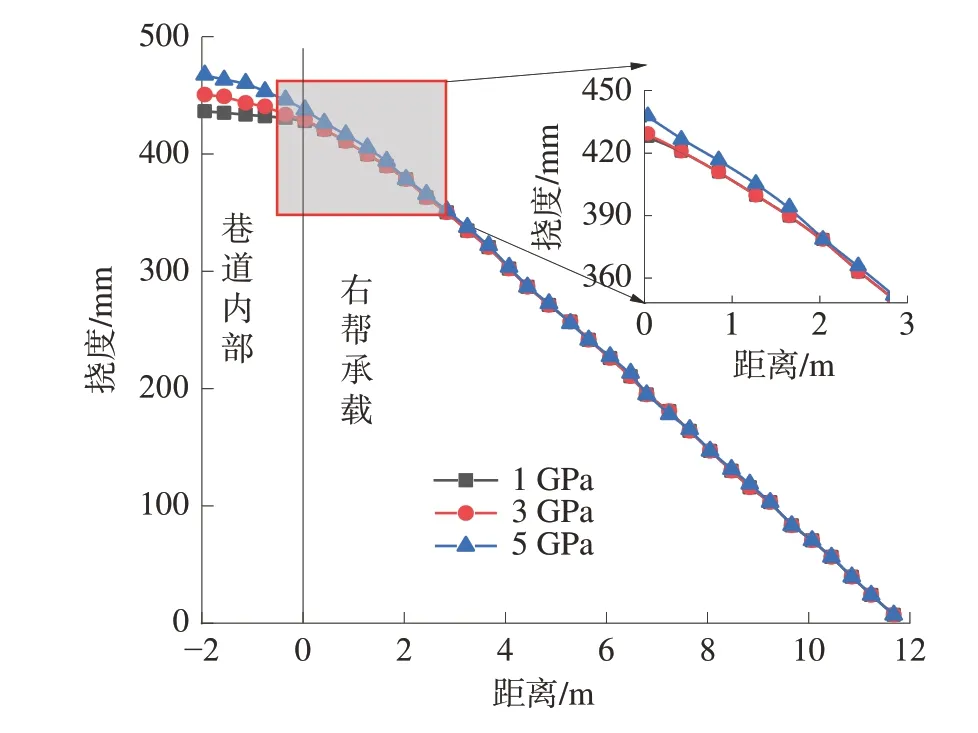
图2 不同顶板弹性模量下挠度分布Fig.2 Deflection distribution under different roof elastic modulus

由图2 可知：随着弹性模量的增大，巷道顶板挠度呈增大趋势，且最大值位于巷道中心线位置；弹性模量为1、3、5 GPa 条件时，顶板最大挠度分别为437.9、452.0、467.5 mm。当弹性模量较低时，适当增加弹性模量可适当减小顶板挠度；不同弹性模量对巷道内部顶板挠度影响较大，但基本不影响右帮承载区顶板挠度分布特征。

1.3 两帮弹性模量对顶板变形的影响

弹性地基系数由两帮岩体弹性模量及厚度决定，不同两帮岩体弹性模量条件下顶板挠度如图3。

图3 不同两帮弹性模量条件下顶板变形特征Fig.3 Deflection distribution under different elastic modulus conditions

由图3 可知：两帮岩体弹性模量对顶板变形及稳定性具有显著影响；顶板最大挠度随着两帮岩体弹模的增大呈现指数型减小趋势，两帮岩体弹性模量为0.5、1、2、3 GPa 下对应的顶板最大挠度分别为860.4、436.6、292.5、212.2 mm，表明两帮弹模较低时，小幅度提升弹模也会大幅度降低顶板挠度；两帮岩体弹模大于2 GPa 后，巷道中心线最大挠度值变化不大。两帮岩体弹模对巷道内部及右帮承载区挠度均有较大影响。

1.4 两帮地基厚度与应力峰值对顶板变形的影响

不同地基厚度和超前应力峰值条件下顶板变形特征如图4。

图4 不同地基厚度和超前应力峰值条件下顶板变形特征Fig.4 Deformation characteristics of roof under different foundation thicknesses and stress peak values

弹性地基系数和地基厚度呈负相关关系，因此随着弹性地基厚度的增大，顶板挠度呈现线性降低趋势，随着距离巷道中线距离的增大，挠度值逐渐减小。不同地基厚度和巷道沿顶、底掘进方式相关性较大，沿顶掘进一般对应巷道高度，沿底掘进对应煤层厚度。

对比不同顶板、两帮强度下顶板弯曲变形特征可知：当两帮岩体刚度较低时，顶板变形主要由两帮岩体刚度控制，即两帮可变形支承主控顶板变形。而当顶板刚度较低时，仅对巷道上方区域顶板挠度产生相对较低影响，考虑到软弱岩石的流变效应，应及时采取护表、注浆等加固措施以保持巷道的长期稳定性。

超前支承压力峰值对顶板变形产生显著影响。支承压力峰值由15 MPa 增加至25 MPa 时，顶板中心线最大挠度由570.2 mm 增加至1 131.2 mm，巷帮最大挠度由544.1 mm 增加至1 069.3 mm，表明超前支承压力峰值对两帮及巷道悬梁挠度影响较大。

超前支承压力和开采参数、开采顺序等相关性较大，正确评估超前应力集中系数对于超前段巷道支护、围岩控制具有重要意义。

2 超前支承压力演化及敏感性分析

2.1 数值计算模型及方案

不同地质参数、开采参数及开采方法对应不同的超前支承压力分布与不同的覆岩运移特征。主要分析埋深、采高、工作面长度（面长）三因素对超前支承压力的影响，采用正交分析的方法对三因素进行分析。FLAC 数值计算模型长×宽×高分别为500 m×400 m×200 m，模型边界为40 m，模型四周固定水平方向位移，底边固定垂直、水平方向位移，顶边为自由边界。数值计算模型如图5。数值计算参数见表1，数值计算方案见表2。

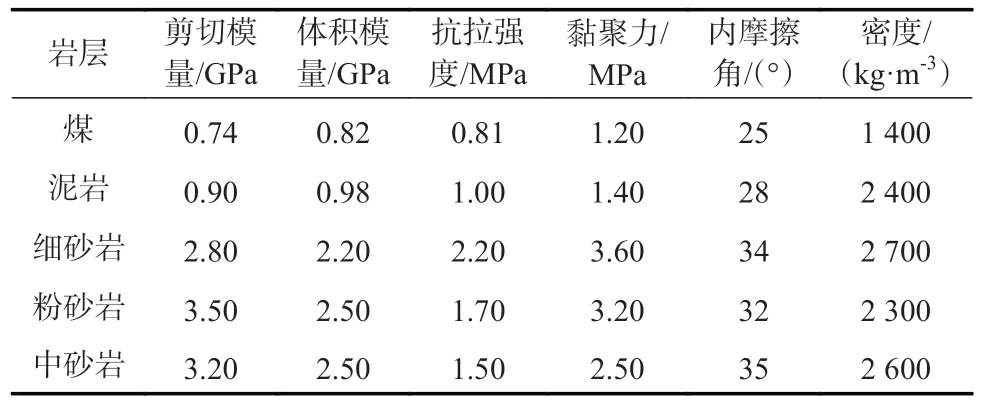
表1 岩体力学参数Table 1 Mechanical parameters of rock mass

表2 数值计算正交设计方案Table 2 Orthogonal design schemes for numerical calculation

图5 数值计算模型Fig.5 Numerical calculation model

2.2 采动超前支承压力分布规律

葫芦素煤矿是中天合创能源有限责任公司，生产能力为8.0 Mt/a，21104 工作面长度为320 m煤厚约为3.2 m，埋深约为700 m，顶板条件较为破碎，超前段顶板发生断裂、破碎及垮落，围岩整体变形量较大，肩窝剪切滑移明显，数值计算中为体现破碎顶板条件，将顶板细砂岩强度进行折减，尽管存在不合理之处，但一定程度可表征破碎顶板的影响。所有模拟方案中，方案5 最接近其地质条件，选取方案5 进行细致分析。不同推进距离超前支承压力分布如图6，不同推进距离超前支承压力集中系数分布如图7。

图6 不同推进距离超前支承压力分布Fig.6 Advance bearing pressure distribution at different propulsion distances

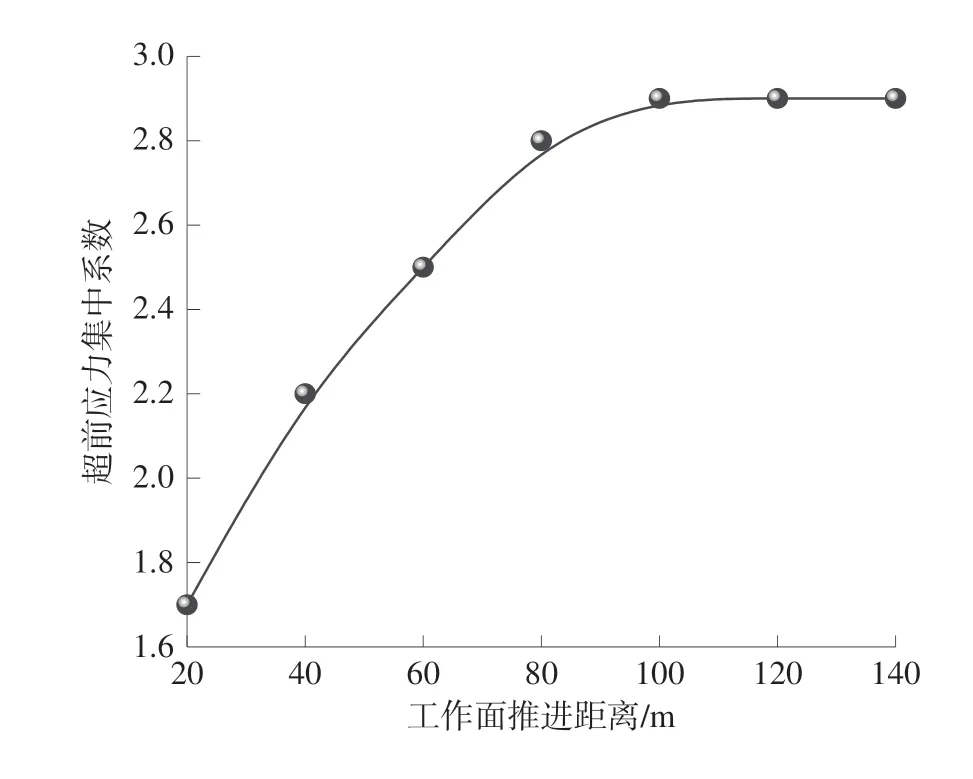
图7 不同推进距离超前支承压力集中系数分布Fig.7 Distribution of pressure concentration coefficient for advanced support at different propulsion distances

由图6 可知：超前支承压力峰值随着推进距离的增大而不断增大，推进80 m 时已基本稳定，之后超前支承压力小幅度波动；推进20、40、60、80、100、120 m 时超前支承压力分别为29.8、39.2、44.1、49.7、50.1、51.1 MPa；其中，工作面前方2.0～3.0 m 范围内为应力降低区，主要是由于煤壁进入塑性破坏，应力向煤壁深处转移；10～35.0 m 范围内为超前支承压力显著增大区，这也是超前支护需要。

由图7 可知：工作面埋深约700 m，垂直方向原岩应力约17.5 MPa。工作面推进至20、40、60、80、100、120 m 时，应力集中系数呈现先快速增大后缓慢增大趋势，和超前应力较为一致，分别为1.7、2.2、2.5、2.8、2.9、2.9，尽管超前应力集中系数不高，但应力值相对较大，应注重超前支护的有效性。

3 注浆加固围岩稳定性控制技术

3.1 注浆加固思路及技术参数

由顶板弯曲弹性地基梁力学模型可知，顶板较为破碎时(岩性软弱)，增加顶板强度是1 种有效的控制巷道上方顶板变形措施。同时，两帮岩体的强度是控制顶板整体变形的关键要素。在高超前支承压力条件下弹性地基可变形程度较大，形成高水平应力集中，促使顶板向巷道内部挤压变形。根据数值计算结果可知，采高是超前支承压力的主要敏感性因素，但是为了避免煤炭资源浪费，一般需要将工作面区域全部采出。因此，控制采高不是1 个高效经济的技术手段。

注浆加固围岩已在破碎回采巷道超前支护放面成功应用，注浆锚索的间排距和浆液扩散半径相关性较大，以新窑矿、平煤六矿及赵楼煤矿顶板注浆锚索加固技术参数（间排距分别为1 200 mm×1 600 mm、 1 500 mm×1 400 mm、 1 600 mm×1 600 mm）为参考[22]，结合葫芦素煤矿顶板较为破碎条件及与大巷道尺寸(5 400×3 800 mm)特征。确定顶板支护采用间排距为830 mm×700 mm让压锚杆配合间排距为1 660 mm×700 mm 的注浆锚索进行支护（3-2-3 布置），锚杆、锚索长度分别为2 400 mm、6 300 mm。两帮及顶板铺设金属网，具体参数如图8。

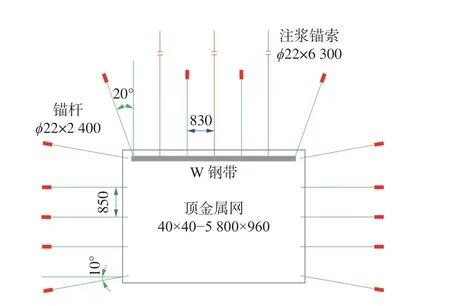
图8 注浆锚索超前支护参数Fig.8 Grouting anchor cable advance support parameters

3.2 注浆加固超前支护控制效果检验

为了验证采用注浆锚索超前支护技术手段的可行性及支护参数的合理性，于21104 工作面回风巷布置3 个锚索测点与2 个围岩变形测点，测点间距为30 m。围岩变形及锚索应力演化如图9。

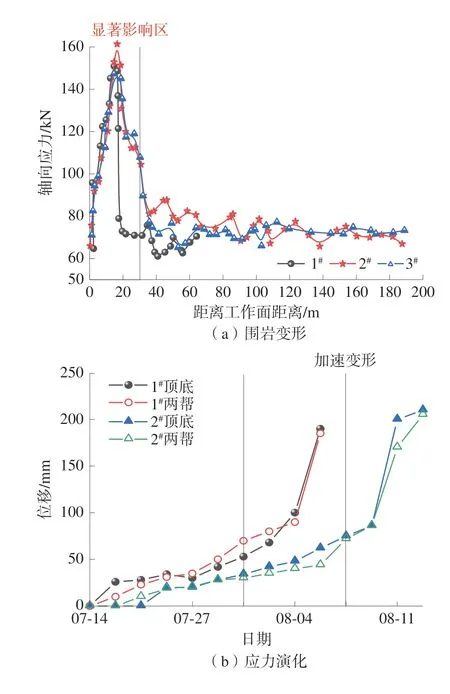
图9 围岩变形及锚索应力演化Fig.9 Deformation of surrounding rock and stress evolution of anchor cable

锚索应力变化的根本原因为超前应力的演变，直接原因为巷道围岩的形变。锚索测站安装完毕时，轴向应力处于小幅度波动状态。随着工作面的推进，锚索轴向应力大幅度增大，工作面前方30～35 m 范围内轴向应力显著提升，这和数值计算结果较为一致，随后由于围岩破碎轴向应力大幅度降低。1#、2#、3#测站锚索轴向峰值应力分别为150.2、167.2、147.3 kN，此时锚索仍具有较强的富裕系数。由测点的位移变化可以看出，距离工作面30 m 左右时巷道围岩处于加速变形阶段，1#测点两帮、顶底位移稍小于2#测点，但均在210 mm 以内，表明注浆锚索性能可以较好发挥，可以有效承载巷道围岩及控制围岩变形，提升超前段巷道稳定性。

为了进一步验证注浆锚索围岩-浆液耦合特征及顶板裂隙发育情形，于1#锚索应力监测点处巷道顶板左侧两注浆锚索中点向顶板上方垂直钻进ϕ50 mm 窥视钻孔。采用钻孔电视方法对顶板6.0 m 范围内进行围岩进行探测，钻孔窥视及支护效果如图10。

图10 钻孔窥视及支护效果Fig.10 Borehole peeping and support effect

由图10 可知：不同层位顶板裂隙发育程度较低，仅在顶板上方1.0 m 位置出现少量裂隙，在巷道顶板上方3.0、6.0 m 位置出现白色半圆环浆液，顶板上方无明显离层现象，这和巷道围岩位移监测结果较为一致。同样证明了采用注浆锚索可有效封堵裂隙，提高围岩稳定性。

4 结 语

1）基于构建的超前段巷道悬梁与弹性地基梁力学模型，揭示了顶板弯曲变形机制，确定了超前应力和弹性地基刚度是顶板变形主控因素。

2）巷道两帮岩体刚度较低时，两帮大变形将加剧顶板弯曲；顶板刚度较低时，仅对巷道上方悬梁顶板产生影响，应及时采取护表、注浆等加固措施以保持长期稳定性。

3）超前支承压力及集中系数随工作面推进呈现先快速增大后缓慢增大趋势，最终趋于平稳，超前应力集中系数不高（2.9），但应力值相对较大（51.1 MPa），应注重超前支护的有效性。

4）试验工作面超前应力显著影响区距离在35 m 范围内，采用注浆锚索加固后顶底板及两帮位移均在210 mm 范围内，巷道上方岩层整体性较强，验证了注浆加固技术手段的可行性与有效性。