顺向正弦来流条件下圆柱气动力和绕流流场数值模拟研究
2024-04-11于春放靖洪淼王仰雪张记涛邵林媛刘庆宽
于春放, 靖洪淼,2,3, 王仰雪, 张记涛, 邵林媛, 刘庆宽,2,3
(1. 石家庄铁道大学 土木工程学院,石家庄 050043;2. 石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043;3. 河北省风工程和风能利用工程技术创新中心,石家庄 050043)
随着大跨度桥梁等工程的飞速发展,自然风的影响日渐显著[1-2]。西堠门大桥[3]的涡激振动现象和虎门大桥的涡激振动事件[4]都对桥梁结构正常运营监测产生了一定影响,甚至影响了城市交通。自然风在遇到建筑物或山丘海岛时,由于物体表面黏性力,风受剪切力改变原有运动状态可能会产生明显卡门涡街现象,从而风场环境发生改变。众多现场观测发现实际自然风场是一种时均风速不断变化的阵风。为达到对风场环境的真实模拟,风洞试验常采用尖劈、粗糙元或格栅等方式增大来流湍流度。但在以往研究中受限于试验设备和方法,常常采用准定常来流进行试验。现需要更加真实地模拟自然界多变的湍流环境。
开展正弦顺向来流条件下圆柱气动力和绕流流场特性研究,不但可以直接应用于解决海洋工程问题,而且可以作为研究湍流作用下钝体气动力特性的出发点。同时在数学上,湍流在时域的速度脉动可以分解为一系列简单的三角脉动函数,即三角级数。虽然单一正弦脉动来流仅仅包含一个速度脉动频率成分,但是可以为研究复杂湍流对钝体气动力和绕流流场特性的影响提供启示作用[5]。王丽等[6]在环境风洞中使用粒子图像速度仪对正弦来流条件下的大气表面层平均风速廓线和湍流强度进行了测量,验证了自然风可看成是由众多不同振幅和周期的正弦风谱叠加。Cao等[5]研究了不同KC(Keulegan-Carpenter)数和振幅比的正弦来流对圆柱升阻力系数,以及旋涡脱落频率的影响规律,但是其来流频率保持不变,而来流频率的变化势必会对旋涡脱落频率等产生重要影响。Ma等[7-8]研究正弦顺流对宽高比5 ∶1矩形柱体的气动力影响,得到正弦顺流会对卡门涡街产生抑制,且正弦顺流和柱体运动频率一致产生耦合现象。Wu等[9]通过大涡模拟(large eddy simulation,LES)方法探究正弦顺流中5 ∶1矩形柱体表面旋涡分离、再附现象的变化得到均匀流与正弦顺流中流动压力相似关系。由于矩形结构相对复杂,气动力特性和流场变化规律繁杂,而圆柱绕流模型是流体力学研究的经典课题,大量学者对选取圆柱为研究对象研究绕流模型。战庆亮等[10]采用LES方法研究了均匀来流下Re=3 900圆柱绕流问题,分析了流场的一二阶特性。Lysenko等[11-12]基于开源计算流体力学软件平台OpenFOAMⓒ的LES方法研究Re=3 900的三维圆柱绕流问题,分析尾流特性得到回流区速度分布和脉动特性。Tamura等[13]通过插值法将LES亚网格尺度建模与3D数值结合,详细讨论了Re=1 000时圆柱绕流的复杂流动情况。部分学者也开展了多种形态来流下的圆柱绕流研究。Cao等[14]选取来流风向角度实现剪切来流,研究了Re=1 000时圆柱绕流的剪切效应,得到了斯特劳哈尔数和剪切参数没有明显相关性。谭潇玲等[15-17]分别研究了平面剪切流、展向剪切流和速度剪切流下的圆柱绕流,发现了尾流场旋涡分布变复杂的现象。Wang等[18]研究Re=1 000时串列双圆柱受正弦来流的影响,发现圆柱绕流对正弦来流的振幅十分敏感。
综上所述,本研究开展顺向正弦来流条件下圆柱绕流数值模拟,重点研究来流频率变化对圆柱气动力和绕流流场特性的影响规律,为进一步研究复杂湍流条件下钝体绕流特性提供参考。本文以直径D=1 m的圆柱为研究对象,通过定义不同正弦频率的来流方法实现对正弦来流模拟,采用LES方式对Re=1 000的圆柱绕流进行模拟,将获得的气动力特性、流场参数进行验证分析,从而得到不同频率顺向正弦来流对圆柱绕流气动特性和流场的影响规律。
1 数值模拟设置
1.1 控制方程
采用笛卡尔坐标系建立圆柱绕流流场的数值模型。大涡模拟筛率后的连续性方程和N-S方程,分别如式(1)和式(2)所示,其中网格湍流和亚格子湍流分别进行了求解和模拟。
(1)
(2)
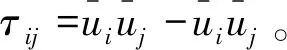
(3)
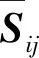
1.2 数值离散和算法设置
为获得可靠的模拟结果,在模拟过程中,梯度项采用高斯线性二阶中心差分格式,散度项采用高斯线性二阶迎风格式,时间离散项采用后台阶二阶隐式格式。另外,在数值计算过程中,采用PISO (pressure-implicit with splitting of operators)算法进行压力和速度耦合计算。各变量收敛值设为1.0×10-6,每个时间步收敛的标志是残差达到收敛精度。无量纲时间步长Δt*=ΔtU0/D(Δ为计算所用的时间步长)为8×10-3,保证最大柯朗数小于1,时间间隔满足要求,保证了计算结果的准确性。
1.3 计算域和边界条件
数值计算域如图1(a)所示,圆柱直径D=1.0 m,圆柱重心为几何中心。上游边界距离圆柱中心10D,下游边界距离圆柱中心20D,上下面边界距离圆柱中心10D。已有研究[19-20]证实,当z轴方向距离为4D时,能够准确地体现绕流流场三维效应。采用结构化网格划分计算域,其中z方向网格均匀划分40层。采用O-Block对圆柱体周围进行网格划分并作加密处理,首层网格高度设置为0.006 m,网格增长率为1.075,满足增长率要求,总网格量为82万。模拟过程中保证了计算y+值平均值小于0.5,最大值不超过1的要求,确保了计算精度。具体网格划分如图1(b)所示。
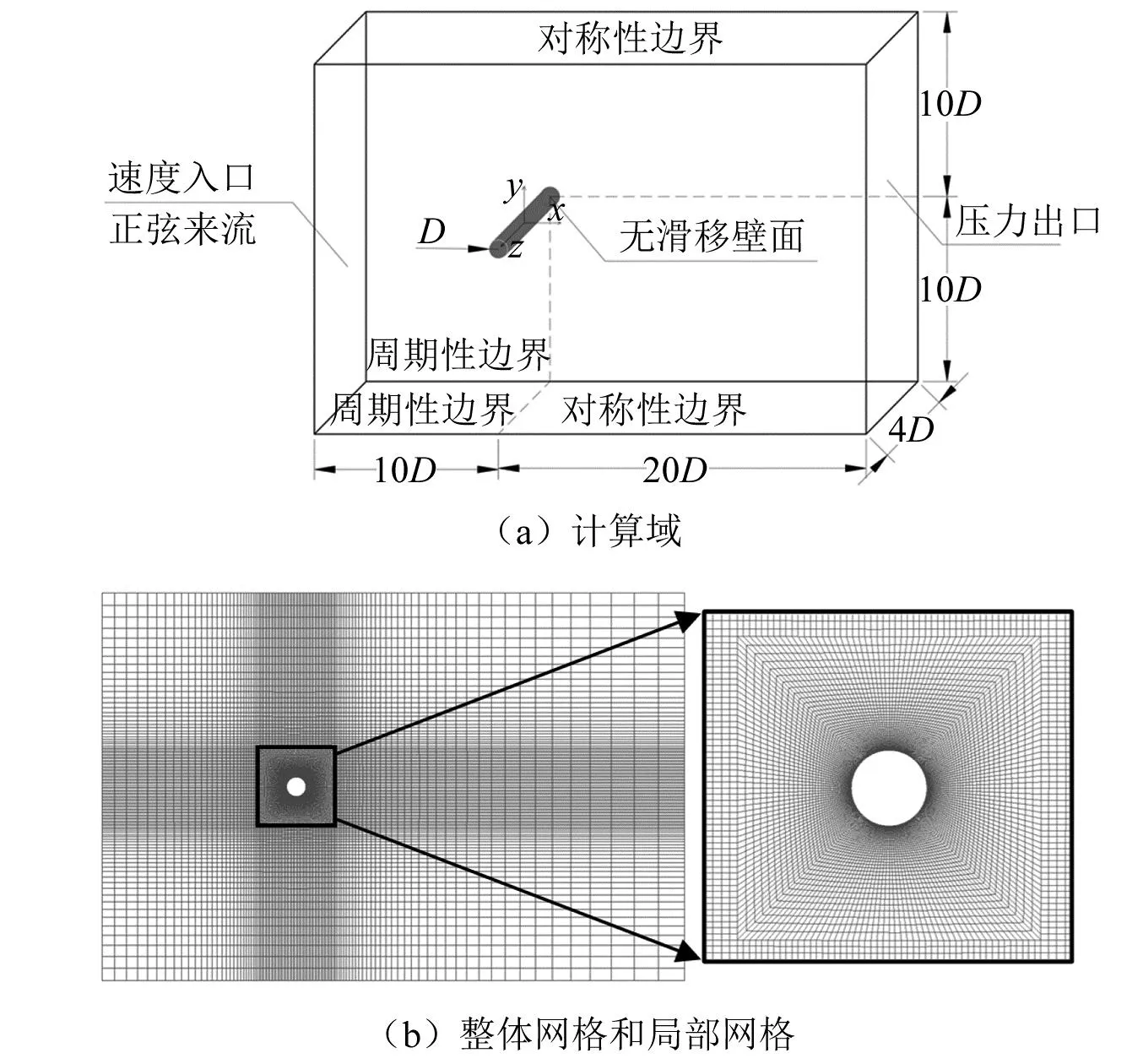
图1 计算域和网格划分Fig.1 Computing domain and grid division
计算域入口采用顺向正弦速度来流条件,选择codedFixedValue方法进行设置。计算域出口采用零压力边界条件。圆柱表面采用无滑移固壁边界条件。上下面采用对称边界条件。前后面采用周期性边界条件。根据雷诺数计算公式Re=U0D/υ=1 000,设来流稳定速度U0=1 m/s,流体密度ρ=1 kg/m3,运动黏度υ=0.001 m2/s。
采用coded Fixed Value方法设置入口不同频率的顺向正弦来流,具体公式如下
U=U0+Asin(2πft)
(4)
式中:振幅A=0.15U0;f为正弦来流的频率,Hz;t为时间,s。
1.4 工况设置
顺向正弦来流频率分别选择f=0、0.05 Hz、0.10 Hz、0.15 Hz、0.20 Hz、0.25 Hz、0.30 Hz和0.35 Hz,其中f=0工况可用于验证试验方法的准确性。另外,为获得均匀来流和顺向正弦来流条件下圆柱绕流状态的差异性,在来流频率f=0~ 0.1 Hz区间进行均匀加密试验,添加f=0.025 Hz和0.075 Hz两组试验工况。
2 数值方法验证
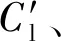

表1 模拟结果与文献结果对比
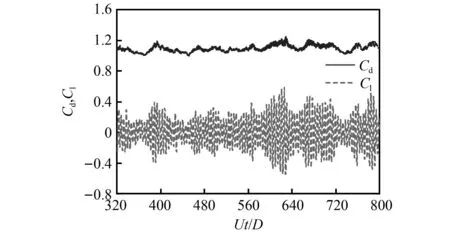
图2 升阻力系数时程图Fig.2 Time histories of lift and drag coefficient
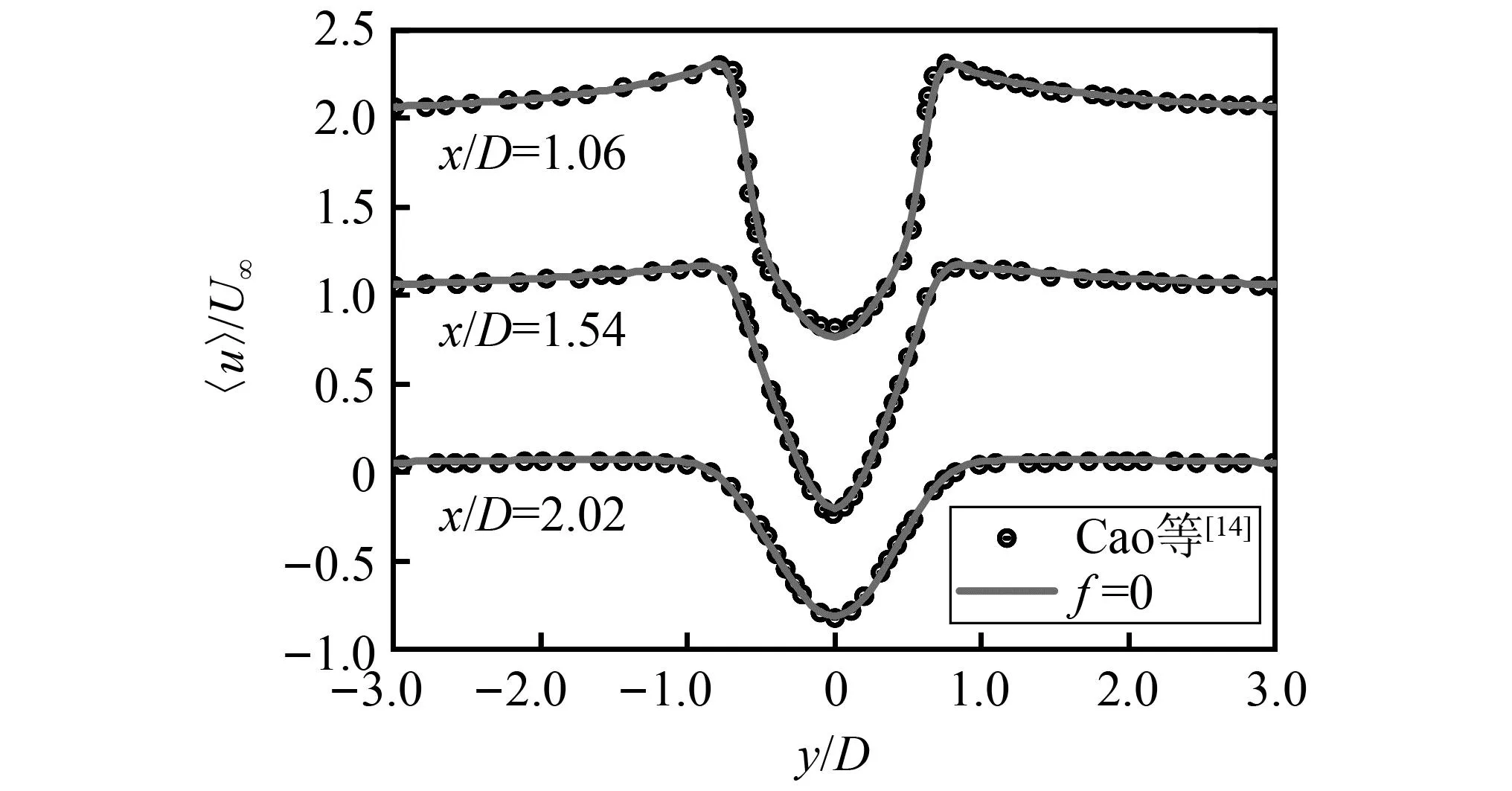
图3 不同位置处时间平均顺向速度分布图Fig.3 Time average forward velocity distribution at different locations
3 数值模拟结果与分析
3.1 气动力及流场特性参数
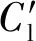
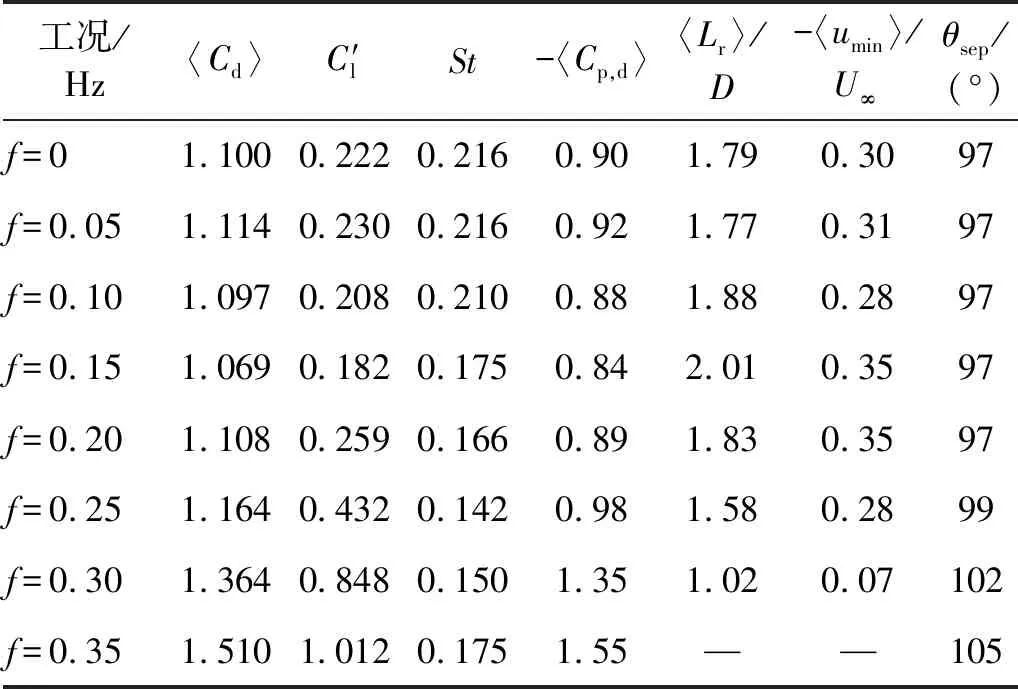
表2 各工况圆柱气动力和流场特性参数
为研究顺向正弦来流和均匀流条件下圆柱绕流的差异性,增加了f=0.025 Hz和0.075 Hz两个工况,实现0.025 Hz差值加密处理。加密工况模拟结果的参数变化情况如表3所示。各工况分离角基本不变,回流长度波动较大,存在先增大后减小再增大的趋势,相应的最小顺向速度也呈现了先增大后减小的趋势,背压也呈现了该变化规律。由于表面压力变化,阻力系数变化较小,但也初步呈现先增大后减小趋势。St随正弦来流频率增大持续减小。
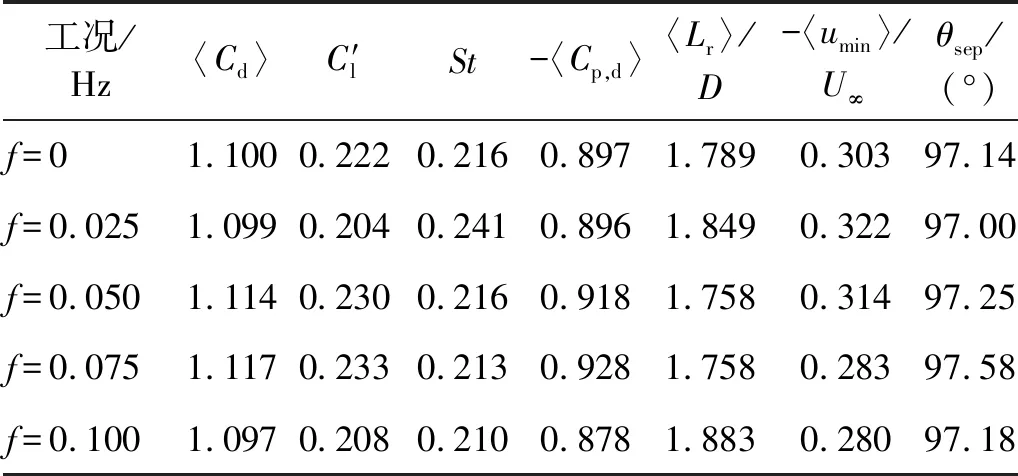
表3 (极)低频工况圆柱气动力和流场特性参数
针对f=0和f=0.025 Hz工况进行详细分析,可见施加正弦波动的顺向来流对圆柱绕流会产生较为明显影响,出现了旋涡分离点变小,旋涡脱落提前,致使回流区增大,回流长度增大3%,最小顺向速度相应增大,同时St增大9%,旋涡脱落频率增大,旋涡脱落加快。因此,较低频率的顺向正弦来流会促使旋涡提前脱落,且脱落速度变快。
3.2 气动力系数频谱分析
3.2.1 阻力系数频谱分析
不同频率顺向正弦来流会对圆柱体的气动力产生影响,需要对气动力系数进行频谱分析。由于顺向正弦来流的正弦波动作用方向为阻力方向,首先对各个工况的阻力系数进行傅里叶变换(fast Fourier transform,FFT)得到相应频谱图。
正弦来流频率f=0、0.1 Hz、0.2 Hz和0.3 Hz工况的阻力系数频谱图如图4所示。如图4(a)所示,入口均匀来流条件下阻力系数频谱图仅有一个主峰,即卡门涡街产生的涡脱主频fvs=0.429 Hz。根据以往研究,圆柱绕流阻力系数的卓越频率大约是升力系数的2倍,即2St。见图4(b)~图4(d),阻力系数频谱图中的卓越频率与顺向正弦来流的频率一致,且有主频2倍频率的峰出现,正弦来流影响强于原有卡门涡街影响,顺向正弦来流呈现主导趋势,一定程度上抑制旋涡脱落的强度。随着正弦来流频率f的增大,旋涡脱落过程中正弦来流影响逐渐加重,阻力系数呈现先变小到逐渐增大。结合图5展示各工况下阻力系数频谱图汇总图,卓越频率峰值随着顺向正弦来流f增大逐渐增大,主导地位加剧。这说明随着顺向正弦来流f增大,正弦来流对圆柱绕流的影响越剧烈,对旋涡脱落的抑制作用越显著。同时对各工况主频振幅进行拟合得图6,得到振幅与来流频率之间变化规律。当顺向正弦来流f>0.075 Hz时,符合线性变化趋势,拟合公式为y/D=2.732f+0.142;当f<0.075 Hz时,基于现有数据为先下降后上升,需要更详细的加密研究。

图4 阻力系数频谱图Fig.4 Drag coefficient spectrum
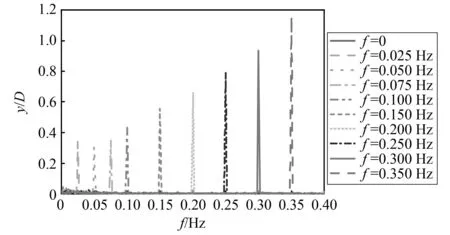
图5 各工况下阻力系数频谱图汇总Fig.5 Summary of drag coefficient spectrum under different conditions
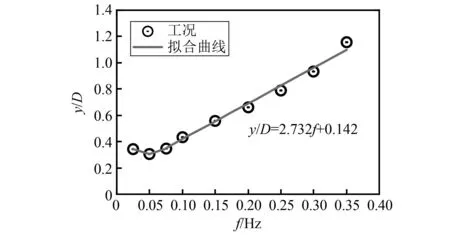
图6 阻力系数主频振幅趋势图Fig.6 Amplitude trend diagram of main frequency of drag coefficient
3.2.2 升力系数频谱分析
针对升力系数进行FFT得到相应频谱图,如图7所示。来流频率f=0工况对应均匀来流时仅有一个主峰(fs=0.216 Hz);其余3组工况下均有多个峰。当顺向正弦来流频率f=0.1 Hz时,卓越频率为fs=0.2 Hz,同时主峰左右两侧各有一个较明显的波峰,左侧波峰满足差频率f-=fs-f=0.2-0.1=0.1 Hz,右侧波峰满足和频率f+=fs+f=0.2+0.1=0.3 Hz。当来流频率f=0.2 Hz和0.3 Hz工况时,来流频率大于体系卓越频率,差频率不存在,所以频谱图中仅有卓越频率峰值和和频率峰值。与均匀来流条件相比,顺向正弦来流条件下圆柱的升力系数会出现多个显著频率的波峰,脱落旋涡更复杂。通过对比图7中后3组工况发现,当来流频率f逐渐增大时,升力系数频谱图中出现会较多波峰且卓越频率逐渐凸显。

图7 升力系数频谱图Fig.7 Lift coefficient spectrum
各工况下升力系数频谱图中卓越频率与明显波峰变化情况如表4所示,其中As、A+和A-分别为主频峰值、和频率峰值与差频率峰值。由图8结果可知,当来流频率f
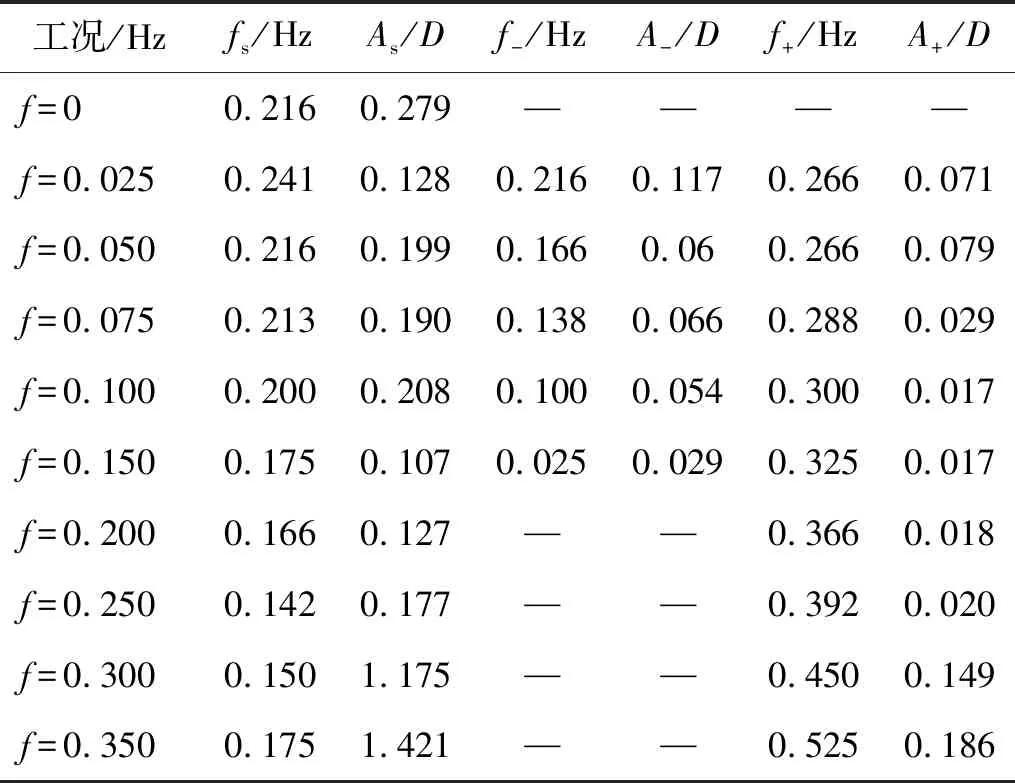
表4 各工况升力系数频谱图中波峰统计
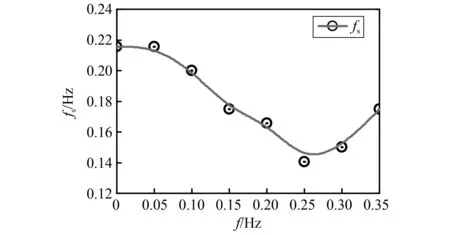
图8 升力系数主频变化趋势图Fig.8 Main frequency change trend diagram of lift coefficient
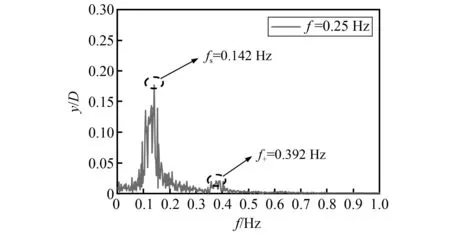
图9 f=0.25 Hz工况升力系数频谱图Fig.9 Lift coefficient spectrum under f=0.25 Hz
3.3 流场分析
3.3.1 时间平均流场
顺向正弦来流相对于以往研究中来流增添了规律性湍流,从而直接影响流体在结构表面以及尾流的流场形态。从机理上分析,绕流流场形态及其发展规律发生改变,会影响结构表面压力分布,从而使结构的气动力系数改变。为更直观分析绕流流场随着正弦来流频率增大的变化规律,分别选取来流频率为f=0、0.1 Hz、0.2 Hz和0.3 Hz时的4组工况进行流场时间平均得到图10所示各工况时间平均流线图。首先分析顺向正弦来流条件下与均匀流场条件下流场结构的差异性。对比f=0与0.1 Hz两组工况,可知顺向正弦来流条件下回流长度出现增大趋势。当来流频率f逐渐增大时,回流长度会逐渐减小,尤其是f=0.3 Hz时,回流长度大幅减小,相对f=0.2 Hz工况回流长度缩短44%。并且观察旋涡中心位置变化,可知随来流频率f增大,旋涡位置前移,旋涡中心相对中间位置,先远离后靠近。在圆柱体背侧近壁面处,随着来流频率f增大,圆柱背侧旋涡逐渐复杂且逐渐变大。在来流频率f=0.3 Hz工况中,背侧旋涡明显增大,原有旋涡直径变小,尾流中有两组对称较大旋涡和一组较小对称旋涡。当正弦来流频率f足够大后,尾流旋涡变得小而多,且回流长度大幅缩短,甚至不出现回流。
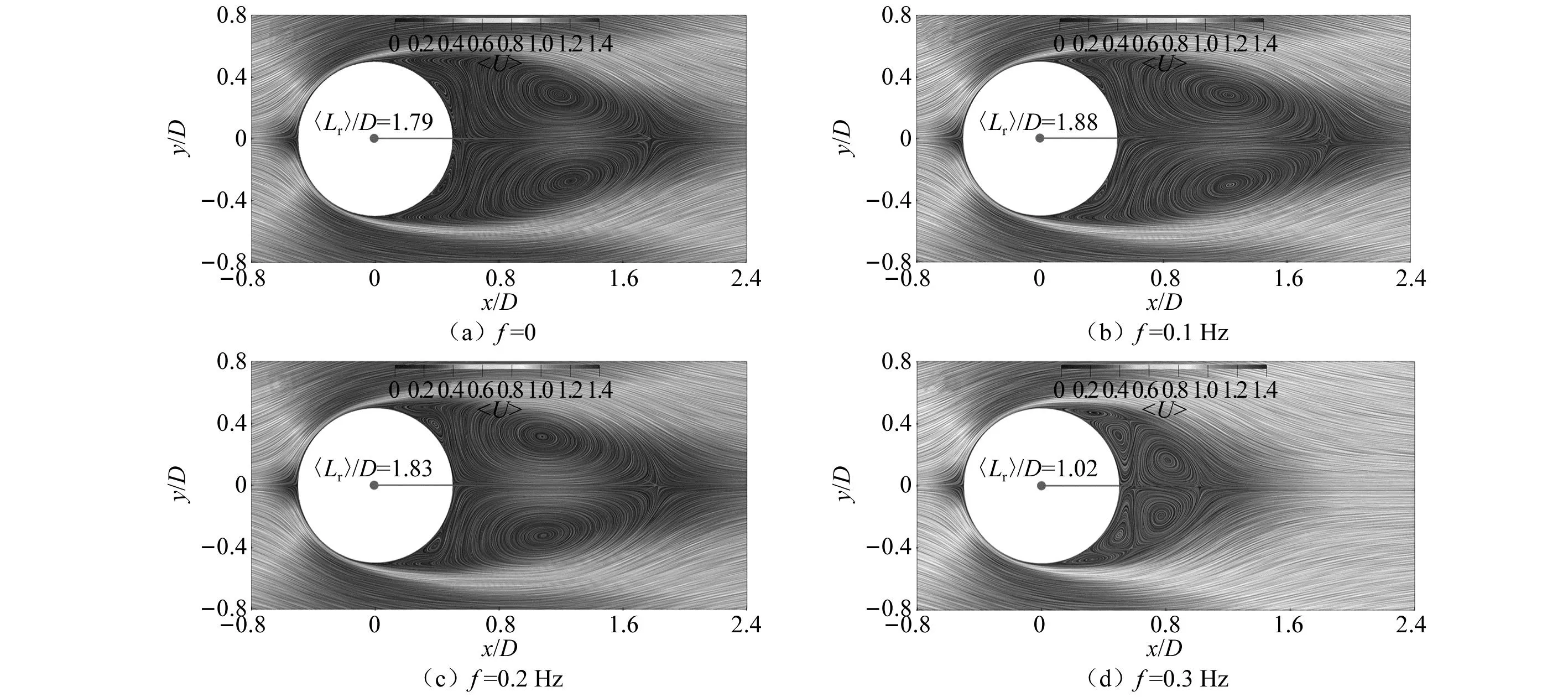
图10 时间平均流线图Fig.10 Time average streamline chart
3.3.2 流场一阶统计特性
各工况尾流中不同位置处速度进行统计均值分析,是研究绕流流场特性的重要内容。在回流区内部,提取了x/D=1.06和x/D=1.54典型位置处数据;在回流区外侧,提取了x/D=2.02和x/D=4典型位置处数据。各工况下不同位置处时间平均顺向速度如图11所示。随着顺向正弦来流频率的增大,各位置处速度变化趋势明显,但存在工况较多、分析总结规律较复杂问题。为此选取频率差值频率为0.1 Hz的几组工况进行分析,同样能够展示速度变化规律。因此,仅选取来流频率f=0、0.1 Hz、0.2 Hz和0.3 Hz时的4组工况绘制了图12中不同位置处速度分布曲线图。
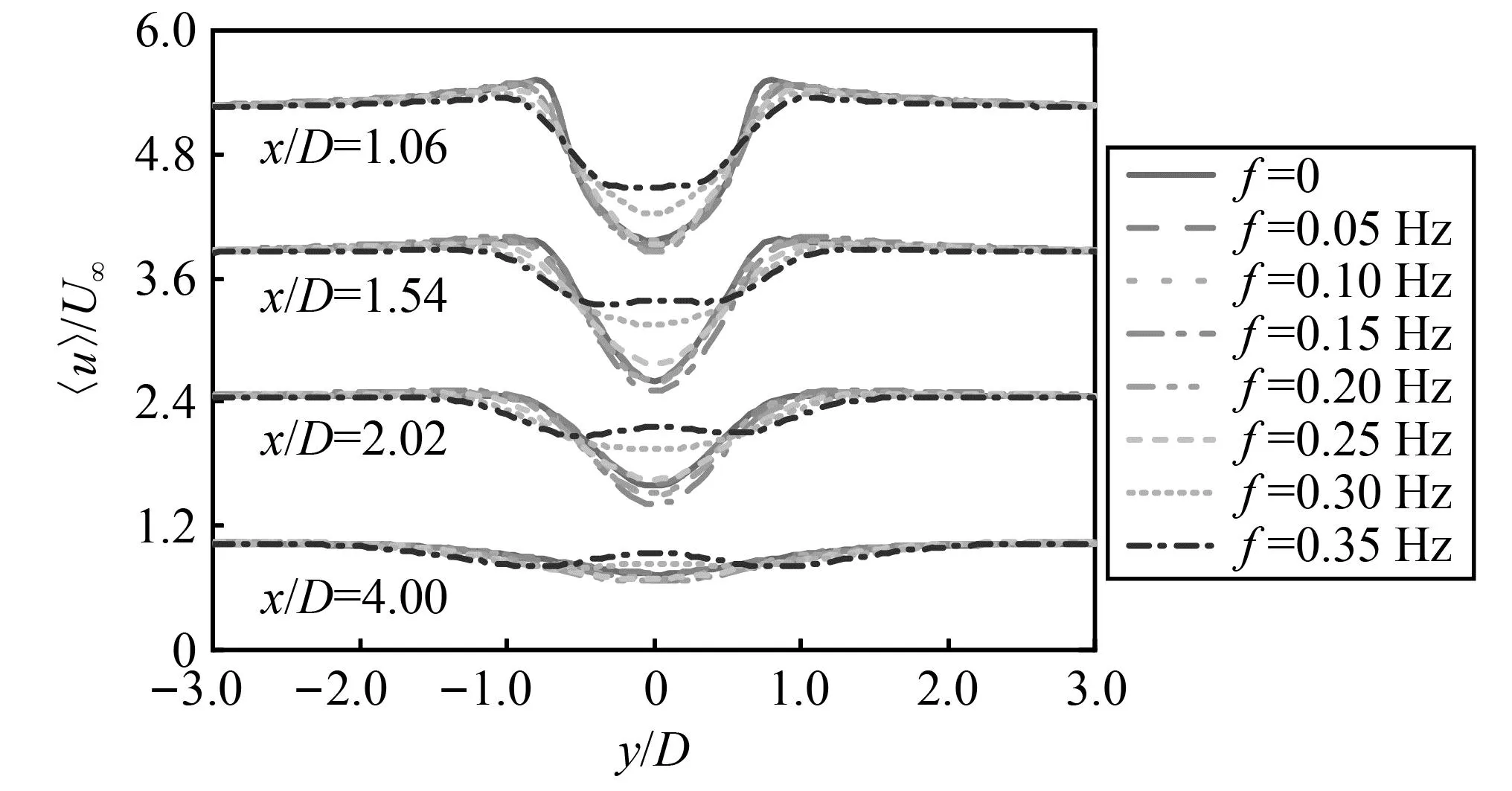
图11 不同位置时间平均顺向速度分布Fig.11 Time average flow velocity distribution under different locations
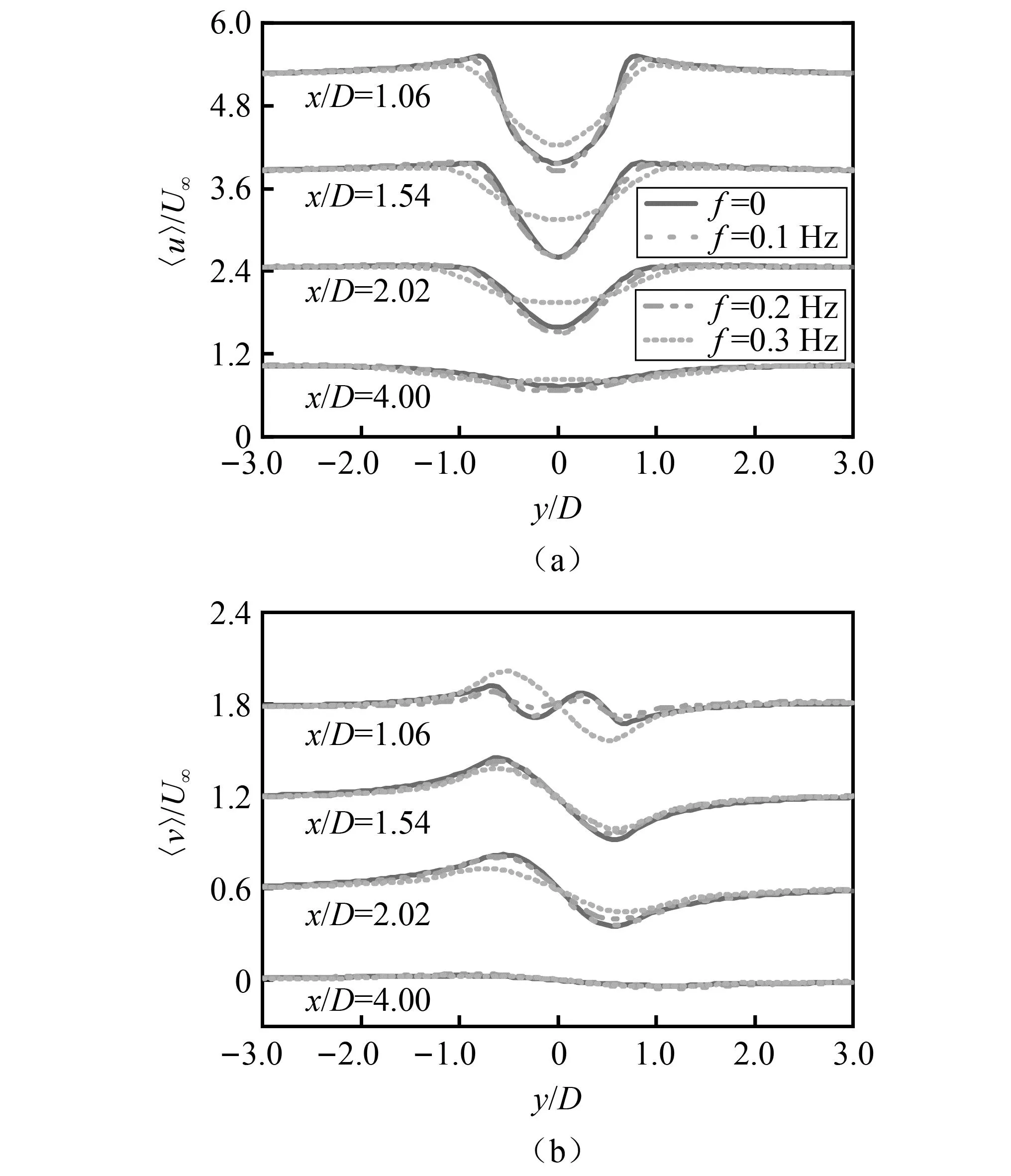
图12 不同位置时间平均速度分布Fig.12 Time average velocity distribution under different locations
流场一阶统计特性,即时间平均顺向速度〈u〉和横向速度〈v〉,分见图12 (a)和图12(b)。前两处典型位置处于回流区内,时间平均顺向速度变化较大。随着正弦来流频率f增大,时间平均顺向速度在回流区同一y/D值位置处的最小速度先变大后减小。结合回流区外的两处位置,可知时间平均顺向速度剖面随着流场的发展由“U”字形逐渐变为“V”字形,其减速效应逐渐趋于平缓。当正弦来流频率增大时,减速区间的变化先逐渐陡峭后逐渐平缓,减速程度先增大后减小,速度稳定位置先逐渐后移后前移。各工况不同位置时间平均横向速度分布见图12(b)。各位置处中仅x/D=1.06位置处横向速度有较明显变化,其余位置处横向速度随着正弦来流频率增大速度波动越平缓,速度稳定位置逐渐提前。在x/D=1.06位置处,在来流频率f 3.3.3 流场二阶统计特性 二阶统计特性能展示流场的脉动值,反映湍流流场的脉动特性。速度的脉动情况是湍流流动的重要特征之一。流场二阶统计特性,即时间平均顺向脉动速度〈u′u′〉和横向脉动速度〈v′v′〉。在模拟工况的控制文件中,设定了计算二阶速度和压力统计量,通过Paraview软件提取不同位置处的二阶统计量,分别如图13(a)和图13(b)所示。其中,不同位置时间平均顺向脉动速度分布见图13(a),各位置处均有两个波峰,对应圆柱尾流存在上下两个对称旋涡。随正弦来流频率增大,不同位置时间平均顺向脉动速度波峰峰值逐渐加大,两峰值位置距离逐渐增大,可知旋涡中速度变大,旋涡中心位置外扩,横向直径有增大趋势。 图13 不同位置时间平均脉动速度分布Fig.13 Time average pulsation velocity distribution under different locations 不同位置时间平均横向脉动速度分布见图13(b),只有一个峰值,可知在尾迹中心线上横向速度脉动量最大。随着正弦来流频率f增大,当f 本研究通过大涡模拟方法,开展了不同频率顺向正弦来流条件下Re为1 000的圆柱绕流数值模拟,研究了圆柱气动力特性和绕流流场随来流频率的变化规律,分析了气动力特性发生变化的机理。主要结论如下: (1)随着顺向正弦来流频率f的增大,圆柱分离角先保持不变,当f>St后逐渐增加。回流长度先增大后减小,当f=0.15 Hz时最大。而St随着来流频率的增加呈现先减小后增大,在f=0.25 Hz时达到最小值。较低频率的顺向正弦来流会促使旋涡提前脱落,且脱落速度变快。 (2)顺向正弦来流在一定程度上可以抑制旋涡脱落的强度。当来流频率f增大时,阻力系数卓越频率下的幅值呈线性增长,该幅值先轻微减小后逐渐增大。另外,当来流频率f (3)正弦来流会改变尾流流场的旋涡形态,增大尾流中的湍流程度。随着正弦来流频率的增大,回流区最小顺向速度和回流长度均先增大后减小,拐点位于f=St左右,整体上时间平均横向速度随f增大逐渐趋于稳定且速度稳定位置提前。随着来流频率f增大,尾流旋涡中时间平均顺向脉动速度变大,旋涡中心位置外扩,横向直径有变大趋势。在近尾流区,正弦来流影响较大,随着来流频率f增大,湍流脉动量逐渐增大;在远尾流区,随着f增大,尾流时间平均横向脉动速度逐渐减小,湍流程度趋于平缓。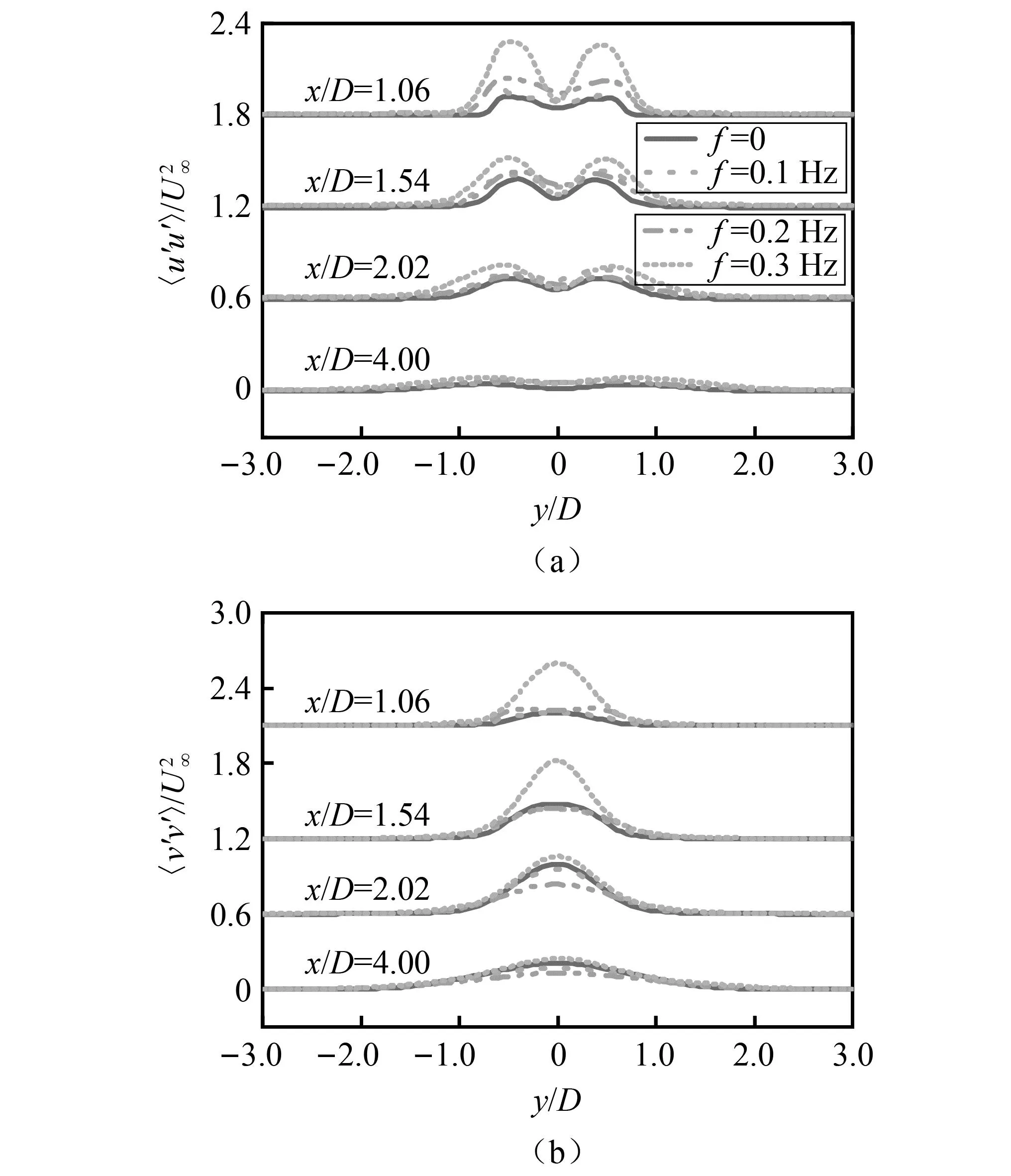
4 结 论
