地震动过程的时域降维建模
2024-04-11阮鑫鑫刘章军姜云木
阮鑫鑫, 刘章军, 姜云木
(1. 信阳师范大学 建筑与土木工程学院,河南 信阳 464000; 2. 武汉工程大学 土木工程与建筑学院, 武汉 430074)
强烈地震往往会导致工程结构坍塌,造成重大人员伤亡和经济损失。为了保障工程结构在地震作用下的安全性和可靠性,通常需要选用一定数量的地震动输入来进行工程结构的动力时程反应分析,因而选用合理的地震动输入时程至关重要。虽然目前已积累了丰富的强震记录,但从中选取适合各种场地和结构的地震动输入时程仍然较为困难[1]。因此,人工地震动模拟成为地震工程领域的研究热点之一。
地震动是典型的随机过程。自Housner首次提出使用随机过程模拟地震动以来,随机地震动模型的研究得到了长足的发展[2-5]。目前,随机地震动模型可分为地震学模型和工程学模型两大类。由于地震学模型需要对地震源和地震波传播路径等物理机制了解,而工程学模型的应用相对简单。因此,本文主要关注工程学模型,此类模型一般有频域方法和时域方法两大主流。频域方法可直接利用地震动的频域统计特性,具有理论完善、计算精度高等特点,便于工程应用。但通过平稳功率谱与强度调制函数的地震动难以体现地震动的时频全非平稳性,而演变过程的时频调制函数除了少数模型[6-7]外,都存在难以参数化估计的问题。随着时频非平稳分析技术的发展,基于小波变换[8-9]、希尔伯特-黄变换[10-11]等时频非平稳地震动模拟方法也逐渐兴起并完善,具有良好的应用前景。与频域方法相比,时域方法无需复杂的频谱分析,具有模拟所需存储空间少、计算效率高的特点,可直接在时域上生成大量的非平稳地震动。然而,无论是频域方法还是时域方法,在进行地震动的随机模拟时,通常需要处理大量的随机变量。例如,谱表示模型中随机相位角的数量取决于谐波分量的数量,而时域过滤白噪声模型[12-13]中包括的高斯随机变量的数量取决于模拟时刻的数量,这导致模拟公式中需要成百上千的随机变量。在这种情况下,通常采用Monte-Carlo方法进行随机抽样,这导致了生成的地震动样本数量巨大以及概率信息不完备,难以应用于工程结构精细化的地震反应和动力可靠性分析[14]。为了减少非平稳地震动过程模拟时基本随机变量的数量,Liu等[15-16]提出了基于谱表示以及基于Karhunen-Loeve分解的降维方法,实现了仅用1~2基本随机变量即可描述原地震动过程。另一方面,上述模型低估了地面运动的自然变异性,因为在此类模型中,通常根据经验将模型参数取为确定性值,而忽略了模型参数的不确定性[17],这将可能导致后续得到结构动力可靠度被高估。
基于上述研究进展,本文拟在平稳过程的时域表达理论基础上,引入随机函数的降维思想,建议一类全非平稳地震动过程的时域降维模型。为了进一步捕获地震动时域降维模型中随机参数的概率分布,基于实测强震记录进行随机参数的样本值识别,利用最大似然估计方法对几种常用的概率分布进行其参数拟合,并通过AIC(Akaike information criteria)准则和K-S(Kolmogorov-Smirnov)检验来确定最优的概率分布。在地震动过程的时域降维模拟时,将时域降维表达中的基本随机变量与模型参数中的随机变量进行统一处理,生成具有赋得概率的代表性点集,进而得到具有相同赋得概率的地震动代表性样本集合,且代表性样本能够体现地震动的自然变异性。同时,地震动过程的时域降维模型在本质上能够与概率密度演化理论相结合[18],进而实现工程结构的精细化动力反应与可靠度分析。
1 地震动过程的时域降维模拟
1.1 平稳过程时域表达的数学理论
任一零均值的实值平稳过程X(t)可表示为如下的Fourier-Stieltjes积分形式[19]
(1)
式中,Z(ω)和U(ω)均为复的正交增量过程,它们的增量分别满足如下条件
E[dZ(ω)dZ*(ω′)]=SX(ω)δωω′dω
(2)
E[dU(ω)dU*(ω′)]=δωω′dω
(3)
式中:E[·]为数学期望;“*”为取复共轭;δωω′为Kronecker符号;SX(ω)为平稳过程X(t)的双边功率谱密度函数。
在式(1)中,H(ω)是一个复值函数,且满足
|H(ω)|2=SX(ω)
(4)
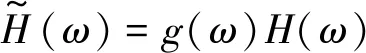
式(1)即为平稳过程X(t)的频域表达形式。进一步,若定义h(t)为H(ω)的Fourier逆变换,即
(5)
可以证明(见附录A),平稳过程X(t)的时域表达形式为
(6)
式中,W(τ)为一个实的正交增量过程,其增量满足
E[dW(τ)dW(τ′)]=2πδττ′dτ
(7)
进一步地,式(6)还可以写成白噪声表达的形式
(8)
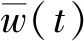
(9)
式中,δ(t-t′)为Dirac函数。
式(8)表明,任意一个实值平稳过程(二阶矩过程)都可以表示为一个过滤白噪声过程。而且,函数h(t)往往与线性时不变系统的脉冲响应函数相关。因此,平稳过程也可看作在白噪声激励下的线性时不变系统的反应过程。
总之,式(1)和式(6)分别在频域和时域上提供了平稳过程的两种等价表达形式。
1.2 地震动过程的时域模型
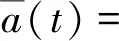
式中:tk=kΔt,k=0,1,…,n;int(t/Δt)=n,Δt为时间离散步长。若T为地震动持时,且int(T/Δt)=N,则n≤N。
在微小时间段ti-1≤t≤ti内,假定h(t-τ)为一常数,同时略去式(10)中的最后一项。于是,式(10)可以近似写成
(11)
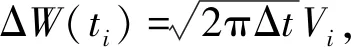
(12)
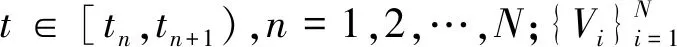
E[Vi]=0,E[ViVj]=δij
(13)
式中,δij为Kronecker符号。
对于全非平稳地震动加速度过程a(t),采用具有随机参数的强度调制函数f(t),以及具有随机和时变参数的函数h(t-τ)来描述时-频全非平稳特性。为此,根据式(12),全非平稳地震动加速度过程a(t)可表示为
(14)
其中,
(15)
在式(14)中,由于求和部分是一个具有时变频率成分的标准化过程(单位方差过程)。因此,强度调制函数f(t)就完全控制了过程的强度非平稳性,而脉冲响应函数(滤波器)及其随机时变参数则控制了过程的频谱非平稳性。由于强度非平稳性和频谱非平稳性的完全分离描述,这为后续的参数识别提供了便利。
1.3 正交随机变量集的降维表达
为了实现地震动过程时域表达的降维模拟,根据随机函数的降维思想,本文建议正交随机变量集的随机函数形式为三角正交基,即
(16)
式中:i,j=1,2,…,N/2;基本随机变量Θ服从区间(0,2π]上的均匀分布;α为任意常数,本文取α=π/3。
在式(16)中,i与j(i,j=1,2,…,N/2)之间存在某种确定性的一一映射关系。这种一一映射关系可采用MATLAB工具箱中的rand(‘state’,0)和randperm(N)函数来实现,即它们的一一映射关系为i=temp(j)。需要指出的是,这一映射关系正是降维方法的一个充分条件。
2 地震动时域模型的参数识别
2.1 模型的参数化
在式(14)中,强度调制函数f(t)采用三段式模型,即
(17)
式中:参数λf=(σmax,t1,t2,c,T);σmax为地震动过程a(t)的标准差函数的最大值;t1和t2分别为强震平稳段的起始和结束时刻;c为控制下降段衰减快慢的参数;T为地震动过程a(t)的持时。
对于平稳地震动的功率谱,采用胡聿贤-周锡元模型[20],即
(18)
式中:ωg和ξg分别为场地土的卓越圆频率和阻尼比;ωh为控制地震动低频含量的参数,可取ωh=2π/T;S0为地震动的谱强度因子,由于式(15)的标准化,可取S0=1。
根据式(4)和式(18),可以给出复值函数H(ω)为
(19)
再根据式(5),并利用留数定理,可得脉冲响应函数h(t)为

(21)
式中,α=ωh/ωg。
对于式(20),其脉冲响应函数h(t-τ)的时变参数λh(τ)=[ωg(τ),ξg(τ)]。其中,ωg(τ)取为关于时间的指数函数[21],ξg(τ)取为常数,即
(22)
式中,λω=(η0,γ)为场地土卓越圆频率的待定参数。
综上,地震动时域模型的参数向量λa=(λf,λh)=(σmax,t1,t2,c,T,η0,γ,ξg)。
2.2 参数识别方法
对于强度调制函数,其控制着地震动过程的幅值与能量。因此,可用地震动的累积能量来对参数λf进行识别。对于第i条实测地震动记录ai(t),其累积能量可表示为[22]
(23)
式中,Ti为第i条实测强震记录的持时。
对于非平稳地震动过程a(t),其累积能量的期望I(t;λf)为
(24)
根据式(23)和式(24),采用最佳平方逼近原则,即可对参数向量λf,i进行识别
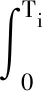
(25)
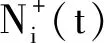
(26)
于是,根据式(27)便可对参数向量λω,i进行识别
(27)
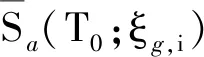
(28)
式中,Tu为反应谱周期的上限,本文取Tu=6 s。
2.3 参数识别结果
在太平洋地震工程研究中心的NGA-West2地震动数据库中,按照如下原则筛选实测强震记录:①断层距离在10~100 km,以减少近场效应的影响以及排除小强度的地震动;②实测强震记录的矩震级应大于6,以排除对结构影响较小的地震动;③实测强震记录的地表以下30 m内平均剪切波速VS,30范围在265~550 m/s[24],对应于GB 18306—2015《中国地震动参数区划图》[25]中的II类场地。
经过筛选得到了31次地震的454条地震动记录。表1给出了本文筛选实测强震记录的地震名称、台站数量、震级、断层距范围和VS,30范围等信息。进一步,对实测强震记录进行四阶Butterworth滤波处理以及截取1%~99%的能量,以保证结果的可靠性。同时,为了便于参数识别,将实测地震动记录的峰值加速度调整为200 cm/s2。
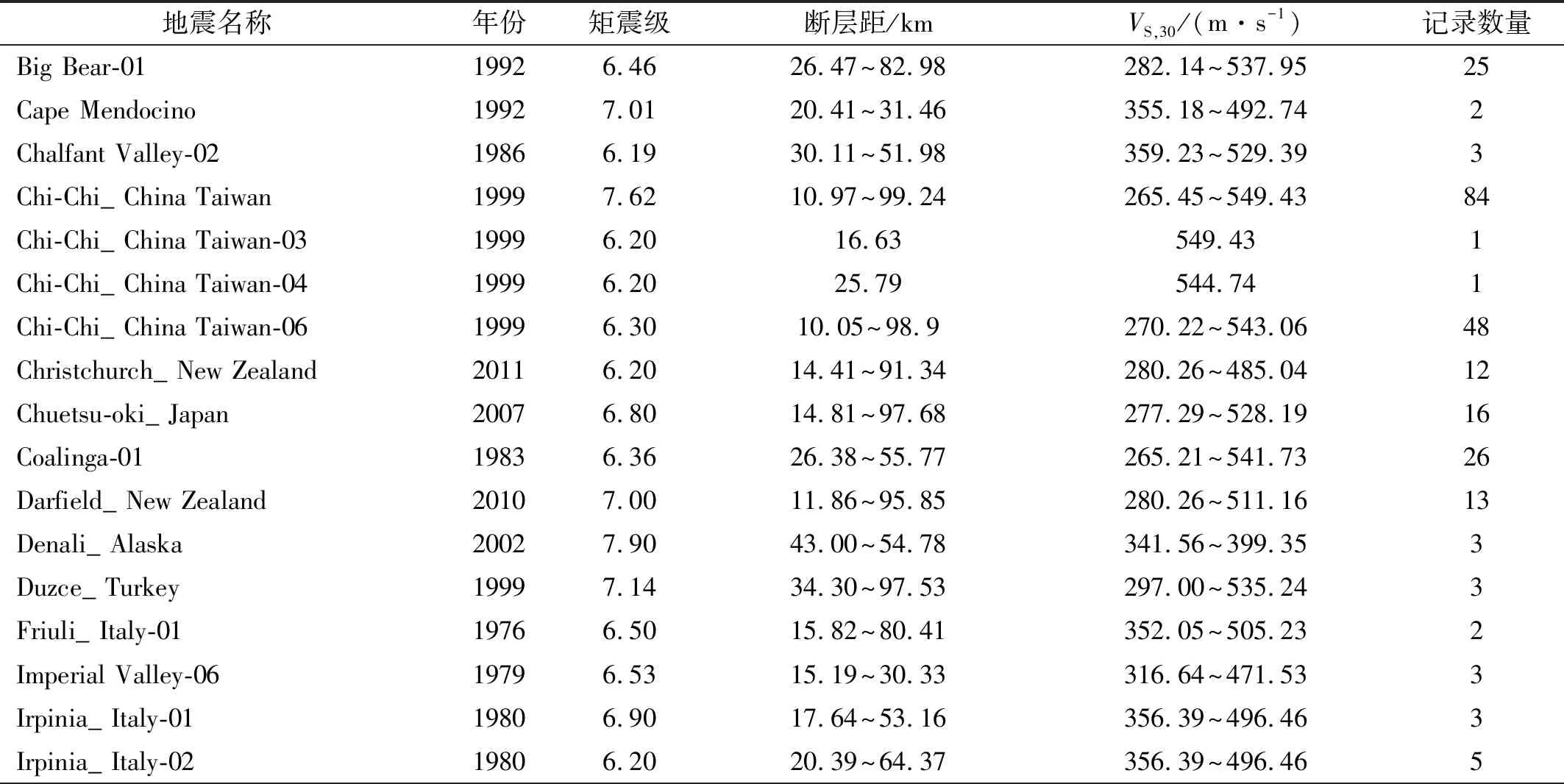
表1 选取的实测强震记录基本信息Tab.1 Basic information of the measured strong motion records
以Taft Lincoln School台站记录的Kern County地震为例,采用上述的时域模型与参数识别方法对地震动的调制函数参数和脉冲响应函数参数进行识别,识别结果如图1。由图1可知:对于累计能量曲线和累计向上穿零次数,模型值与实测值拟合效果良好;对于加速度反应谱,实测反应谱也基本包括在样本反应谱之内,验证了本文参数识别方法的有效性。典型实例的参数拟合结果如表2所示。
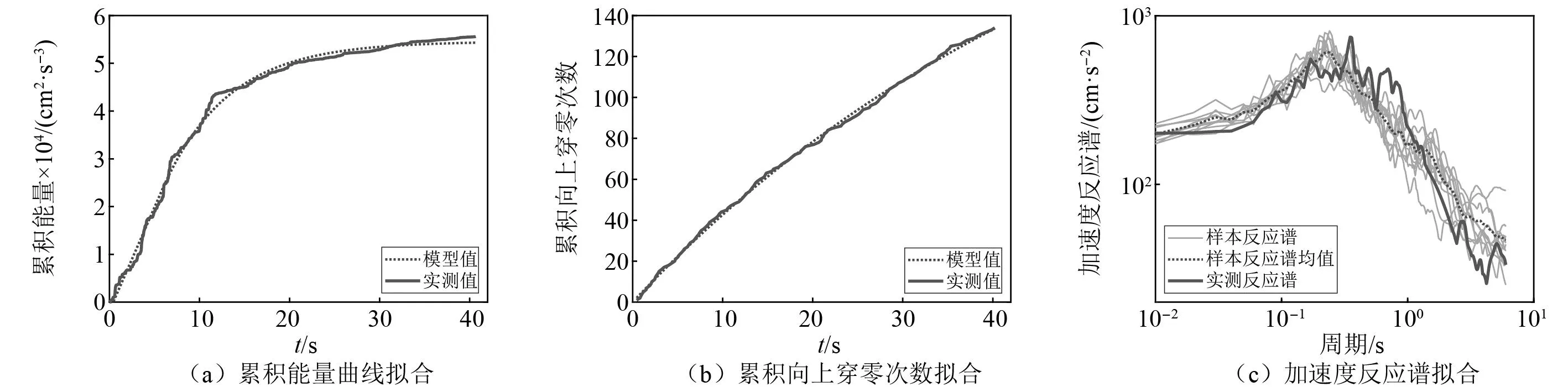
图1 典型强震记录的参数识别Fig.1 Parameter identification of typical strong motion records

表2 典型强震记录的参数识别结果
如2.1节所述,地震动的时域模型中含有(σmax,t1,t2,c,T,η0,γ,ξg)共8个参数。对于所筛选的454条地震波,这8个参数的统计结果如表3所示。为便于分析,表中用ts=t2-t1代替了t2。由表3可知,参数σmax和ξg的变异性相对较小,其他参数的变异性均较大。同时,考虑到持时T在模拟时可直接给定,因此下文仅对参数t1、ts、c、η0和γ等5个参数进行概率密度拟合。此外,由表3可知卓越圆频率函数的衰减指数γ的最小值为负值,这表明实测地震动的主频率并非总是衰减,也可能出现随时间增大的情况。
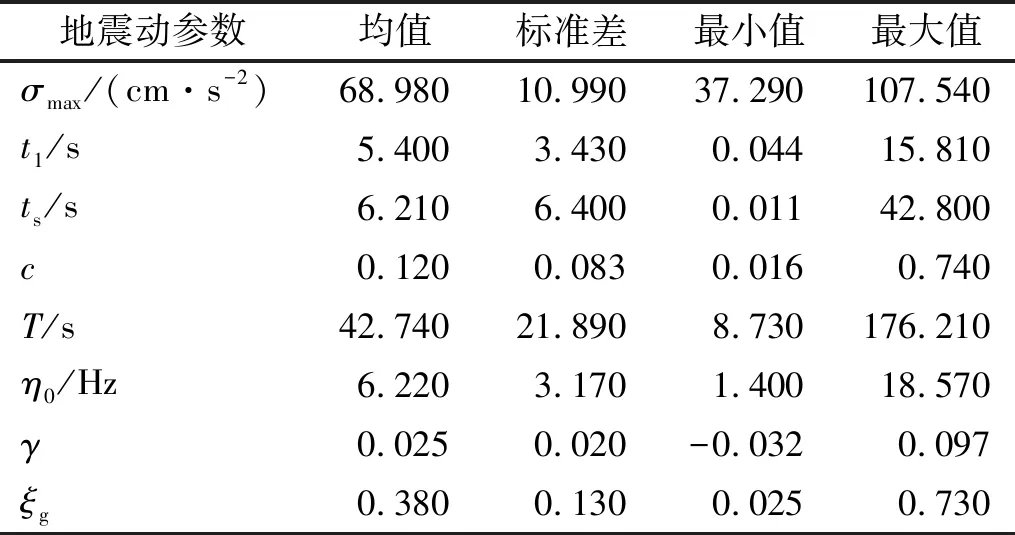
表3 地震动参数的统计结果Tab.3 Statistical results of ground motion parameters
下面分别采用7种概率分布模型对上述5个参数进行拟合,即正态分布、对数正态分布、Gamma分布、Weibull分布、Gumbel分布、广义极值分布和指数分布。通过最大似然估计方法估计分布参数,并通过最小化AIC值[26]来确定最佳拟合模型。然后,再进行K-S检验[27],以判断所获得的模型是否能够真实地表示地震动参数的边缘分布。K-S检验的显著性水平通常取5%。最后,得到参数t1、ts、c、η0和γ的最优概率分布拟合结果如表4所示。

表4 地震动参数的最优概率分布拟合结果
图2给出了参数c的最优概率密度拟合结果。由图2可知,拟合的概率模型能够较好地描述参数c的分布特征。
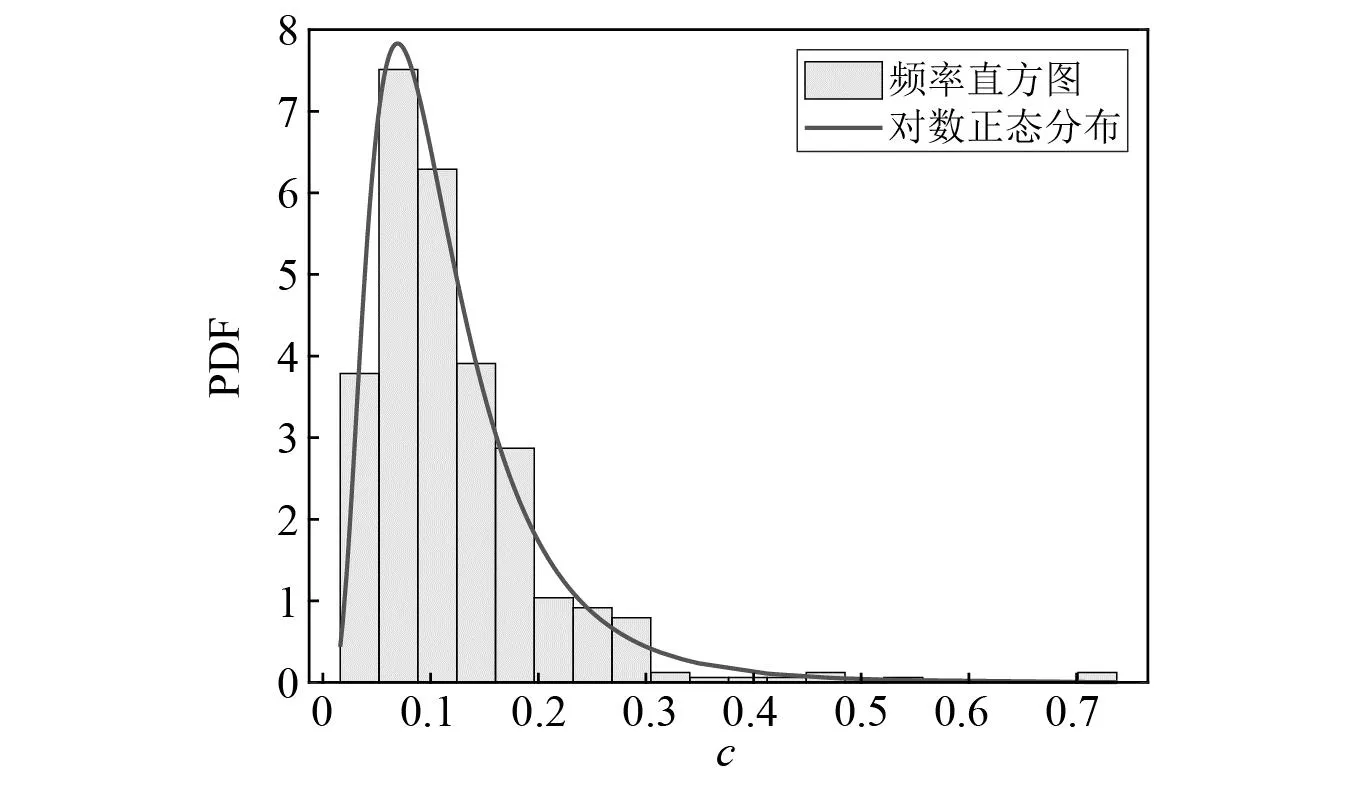
图2 参数c的最优概率密度Fig.2 Optimal probability density of parameter c
3 数值算例
在本算例中,参数t1、ts、c、η0和γ视为随机变量(概率分布见表4),则t2=t1+ts。为简化,忽略参数之间的相关性。参数σmax和ξg取其均值,即σmax=68.98 cm/s2,ξg=0.38。模拟持时取其均值加一倍标准差,近似取为T=60 s。本算例的其他参数为:时间间隔Δt=0.01 s;代表性样本数量为610。
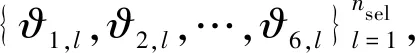
图3给出了本文方法生成的II类场地的代表性地震动加速度样本。从时域特性来看,3条代表性样本的峰值加速度、强震平稳段的起始和结束时刻以及下降段衰减快慢均有显著的差异。从频域特性来看,3条代表性样本的频率成分以及其变化特性也都不同。因此,模拟样本在时域和频域上均具有明显的随机性,反映了实测地震动的自然变异性。
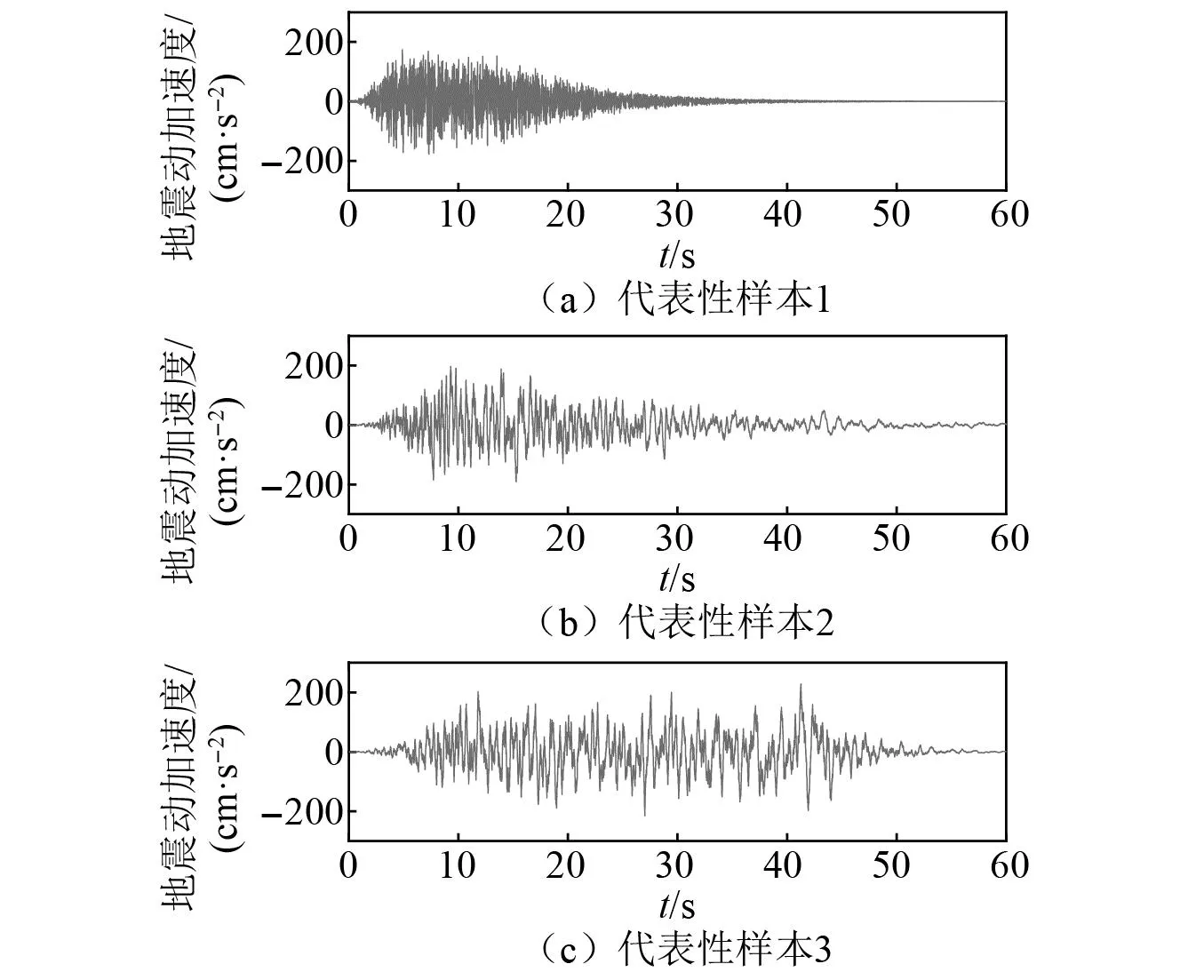
图3 地震动加速度代表性样本Fig.3 Representative samples of ground motion acceleration
图4分别给出了模拟的610条地震动加速度代表性样本集合的均值和标准差与其目标值的对比结果。可见,均值和标准差的模拟值与目标值均对应良好,验证了降维方法的有效性。值得说明的是,尽管式(18)的调制函数为三段式模型,但地震动过程的标准差曲线仍是一个光滑的函数,这是因为在调制函数模型中参数t1、t2和c当作了随机变量。
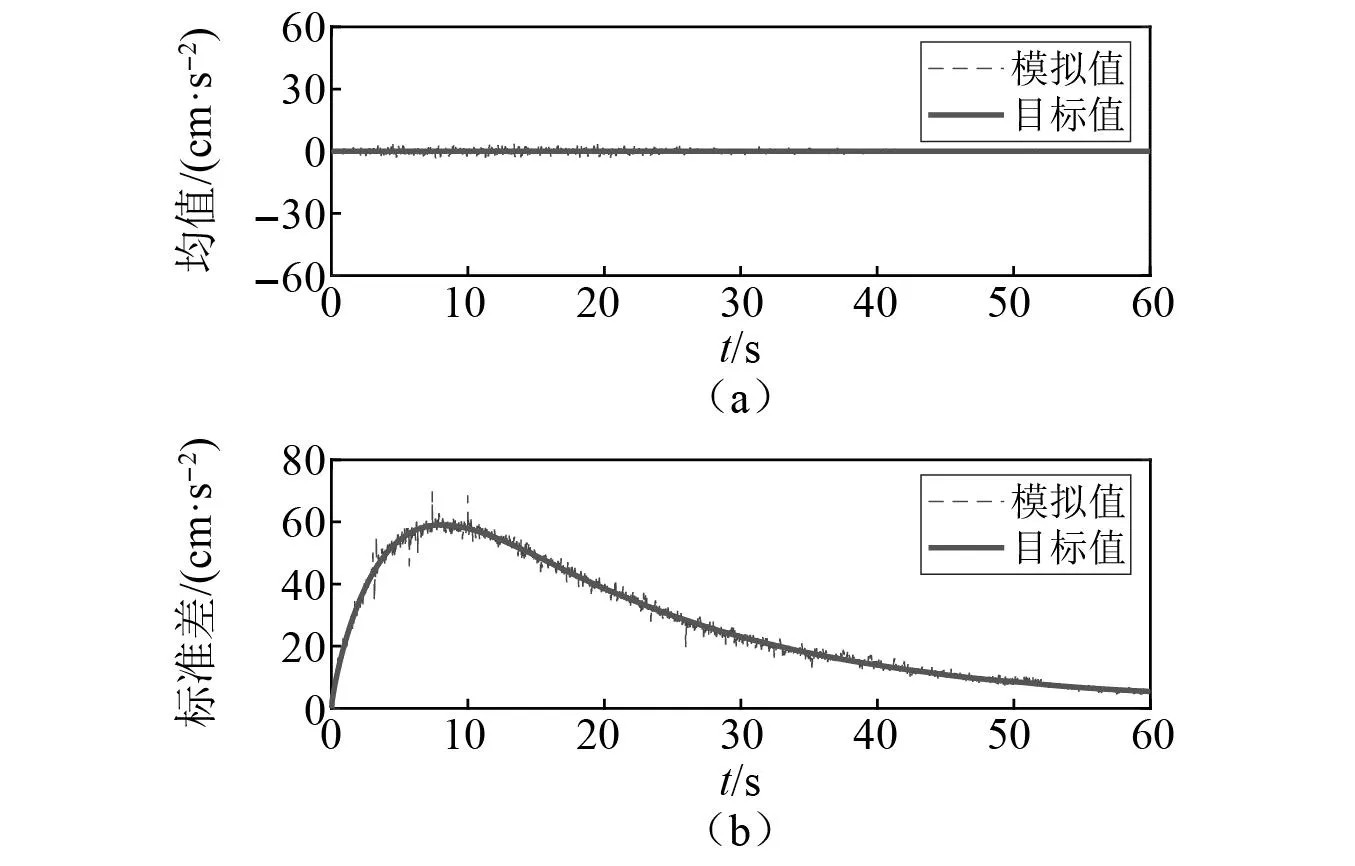
图4 地震动加速度代表性样本集合的均值和标准差Fig.4 Mean and standard deviation of representative samples set of ground motion acceleration
为了进一步分析本文方法的模拟精度,表5分别给出了377、610和987条代表性样本集合的模拟误差,其中均值和标准差相对误差的定义参见Liu等的研究。可见,随着代表性样本数量的增加,均值和标准差相对误差逐渐变小,体现了降维方法的收敛性;当代表性样本数量达到610条时,模拟误差均小于5%,满足精度要求。
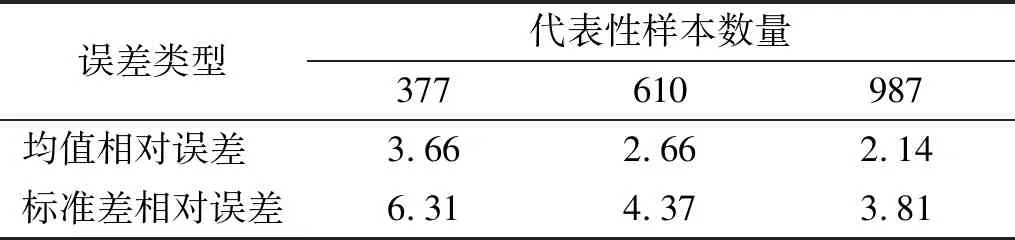
表5 地震动过程的模拟误差Tab.5 Simulation error of ground motion process 单位:%
图5分别给出了本文方法模拟的地震动加速度的反应谱和傅里叶幅值谱与实测强震记录的比较。可以看出,实测强震记录的均值在模拟均值加减一倍标准差范围内,且与模拟均值的拟合较为一致,验证了本文方法具有良好的工程特性。
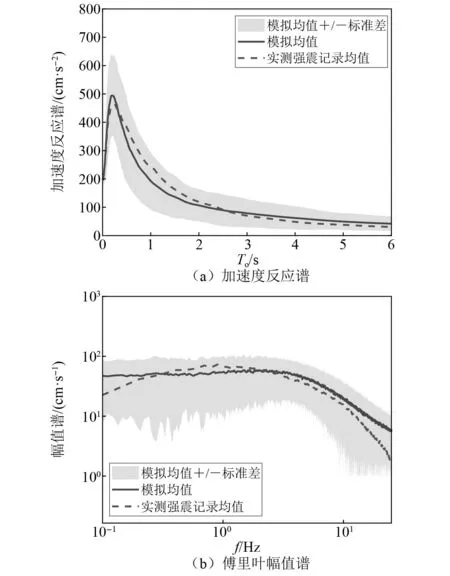
图5 模拟的加速度反应谱及傅里叶幅值谱与实测记录的比较Fig.5 Comparison of response spectrum and Fourier amplitude spectrum between simulated acceleration and measured records
4 结 论
从平稳过程时域表达的基本理论出发,导出了平稳和非平稳地震动的时域降维表达。基于实测强震记录,对地震动时域模型的参数进行了统计建模。通过算例验证了本文方法的有效性,主要结论如下:
(1)通过平稳过程时域表达的推导,阐明了平稳过程在频域和时域上的两种等价表达形式。无论是频域表达还是时域表达,随机过程均是通过一系列正交随机变量所调制的确定性函数的线性叠加来表达的。
(2)通过正交随机变量集的随机函数构造,实现了仅用一个基本随机变量即可精细地表达时域模型的目的,极大地降低了地震动过程的随机度。
(3)建议了地震动时域模型的参数识别方法,通过典型实测强震记录验证了其有效性。根据所选的强震记录,获得了地震动时域模型基本参数的概率密度函数,完善了地震动时域降维建模。
(4)本文方法生成的同一类场地的代表性地震动加速度样本在时域和频域上均具有明显的随机性,能够反映地震动的自然变异性。
附录A
式(6)和式(7)的证明以及原过程的相关函数推导如下。
根据式(5)可知
(A.1)
同时,令
(A.2)
利用式(A.1)和式(A.2),式(1)可写为
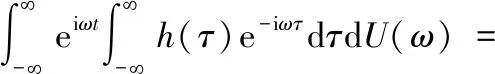
(A.3)
式(6)得证。
由式(A.2)可知
(A.4)
(A.5)
将式(A.5)乘以其共轭后求期望,可得
E[dW(τ)dW*(τ′)]=
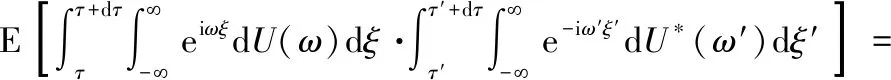
(A.6)
式(7)得证。
于是,原过程的相关函数为
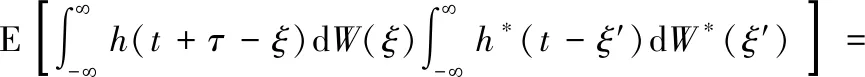
(A.7)
