桥墩沉降下齿轨-超大坡度桥梁系统适应性及安全性研究

陈兆玮, 张梦琪, 王 浪, 李世辉, 袁密奥, 陈志辉, 杨吉忠

(1. 重庆交通大学 机电与车辆工程学院,重庆 400074;2. 中铁二院工程集团有限责任公司科学技术研究院,成都 610031)

高速铁路、地铁等钢轮钢轨制式的轨道交通系统依靠轮轨黏着力实现坡道运行,其极限坡度为35‰,而跨座式单轨等胎轨制式线路的最大坡度可达60‰[1],但依然难以适应山区超大坡度运行条件。而齿轨车辆通过齿轮齿轨间的啮合力为车辆运行提供纵向力,爬升极限坡度可达480‰[2],适用于我国绝大部分山地区域。四川省于2019年5月发布《四川山地轨道交通规划》,规划了23条山地轨道交通线路,其中包含了多座超大坡度齿轨桥梁结构。在桥梁的修建和服役过程中,难免会出现桥墩沉降问题,造成相邻梁体发生竖向位移,进而导致齿轨和钢轨发生竖向变形。由于齿轨许用变形量较小,且与轨枕之间采用螺栓刚性连接,桥墩沉降极有可能诱发齿轨和连接螺栓断裂,导致齿轨支撑刚度不均,齿轮与齿条之间的相互作用力增大,同时,连接螺栓断裂飞溅打击车体,严重影响列车运行安全性[3]。

近年来,国内外学者对齿轨铁路系统动力学开展了部分研究。陈双喜[4]分析了齿轮关键参数和牵引系统驱动方式对车辆动力学性能的影响,以指导后续齿轨车牵引系统设计。牛悦丞等[5]对现有的齿轨的驱动模式进行了归纳总结。Schlunegger[6]对齿轨车辆的发展进行了归纳和展望,并着重讲解齿轨车辆的驱动器、制动器以及相关轨下结构。尚勤等[7]从驱动技术、轨面高度调节技术、减振技术、制动技术、高速进出轨技术等方面预测了发展趋势。黄志相等[8]对齿轨车辆的总体设计,如规划、构造速度、相关技术标准等结合实际情况分析并提出了建议值。赵冠闯等[9]从车体重心高度和转动惯量展开了对车辆动力学性能的研究。陈兆玮等[10]也研究了齿轨车辆-轨道(齿轨)系统的基本振动特性以及轨道随机不平顺对齿轮-齿轨系统动态啮合行为的影响机制。从上述研究可以看出,目前齿轨铁路系统动力学的研究尚处于初始阶段,诸多基本规律和力学特性尚未被深入揭示。

关于桥墩沉降对轨道交通系统的影响,刘宗峰[11]依据TB 10002—2017《铁路桥涵设计规范》和GB 50157—2013《地铁设计规范》,对齿轨铁路设计规范编制中桥梁载荷取值开展相关研究,为后续齿轨-桥梁的分析提供相关依据。刘丽丽等[12]对CRTSⅠ型、CRTSⅡ型和 CRTSⅢ型板式无砟轨道系统对简支梁桥钢轨映射变形和扣件内力对梁体线性变化的敏感性进行研究,得出CRTSⅡ型轨道系统对梁体几何线性变化最不敏感的结论。冯玉林等[13]提出了针对地震引发桥墩沉降与轨道不平顺的对应关系的表达式,并验证该关系表达式的准确性。张鹏飞等[14]找到发生桥墩沉降作用时,CRTSⅡ型板式无砟轨道无缝线路最薄弱位置,为工程建设提供参考。陈天浩等[15]建立了桥墩沉降量与底座板脱空区域映射关系的解析表达式,并验证了其准确性。李龙等[16]研究了梁体徐变和桥墩沉降联合作用对列车响应的影响,指出徐变上拱和桥墩沉降的限制值。李伟强等[17]对桥梁竖向变形引起的中低速磁悬浮轨道不平顺进行了分析。王少杰等[18]研究桥墩沉降、梁体下挠/上拱对轻轨列车单双线运行性能的影响,指出采用Sperling指数对单双线运行方式的影响有更好区分度。王昆鹏等[19]以德国ICE3高速列车为例,对运营阶段列车循环加载导致软土地基桥梁产生附加不均匀沉降威胁行车安全性问题进行研究,找到软土累积沉降发生范围,并指出相邻桥墩沉降引起的桥梁相对上拱对行车安全更不利。陈兆玮[20]也研究了桥梁收缩徐变对桥轨非线性接触行为、轨道层间相互作用、轨道混凝土结构附加动应力以及列车动态特性的影响。虽然桥墩沉降对普通轨道交通的影响规律已有很多研究,但尚未有研究涉及桥墩沉降对齿轨铁路系统影响。而由于齿轨铁路系统关键部件之间的刚性连接设计,桥墩沉降对该系统的影响也成为迫切需要解决的科学难题。

针对桥墩沉降下齿轨-超大坡度桥梁系统的安全性和适应性问题,本文基于列车-轨道-桥梁动力相互作用理论,建立车辆-齿轨(轨道)-桥梁系统的非线性动力相互作用模型,分析在桥墩沉降对Strub型齿轨车辆-齿轨(轨道)-桥梁系统的影响,研究列车通过时桥墩沉降对齿轨垂/纵向变形及应力、连接螺栓应力以及桥梁跨中处齿轨的垂/纵向振动加速度的影响,并最终提出山区大坡度齿轨铁路桥墩沉降安全控制值,为山区铁路设计及运维提供理论支撑。

1 桥墩沉降下齿轨车辆-齿轨(轨道)-超大坡度桥梁系统耦合动力学模型

桥墩沉降会导致与之相邻的两跨梁体发生垂向位移,道床和轨枕会随之下移,导致扣件与紧固件受到向下的附加拉力,进而使钢轨和齿轨由于受到拉力作用而产生垂向变形,易导致齿轨及紧固件出现局部应力过大,严重时还会出现结构损伤断裂等问题,最终影响车辆-齿轨(轨道)-桥梁系统的稳定性和行车安全[21]。齿轨(轨道)-桥梁系统齿轨随桥墩沉降变形原理示意图,如图1所示。

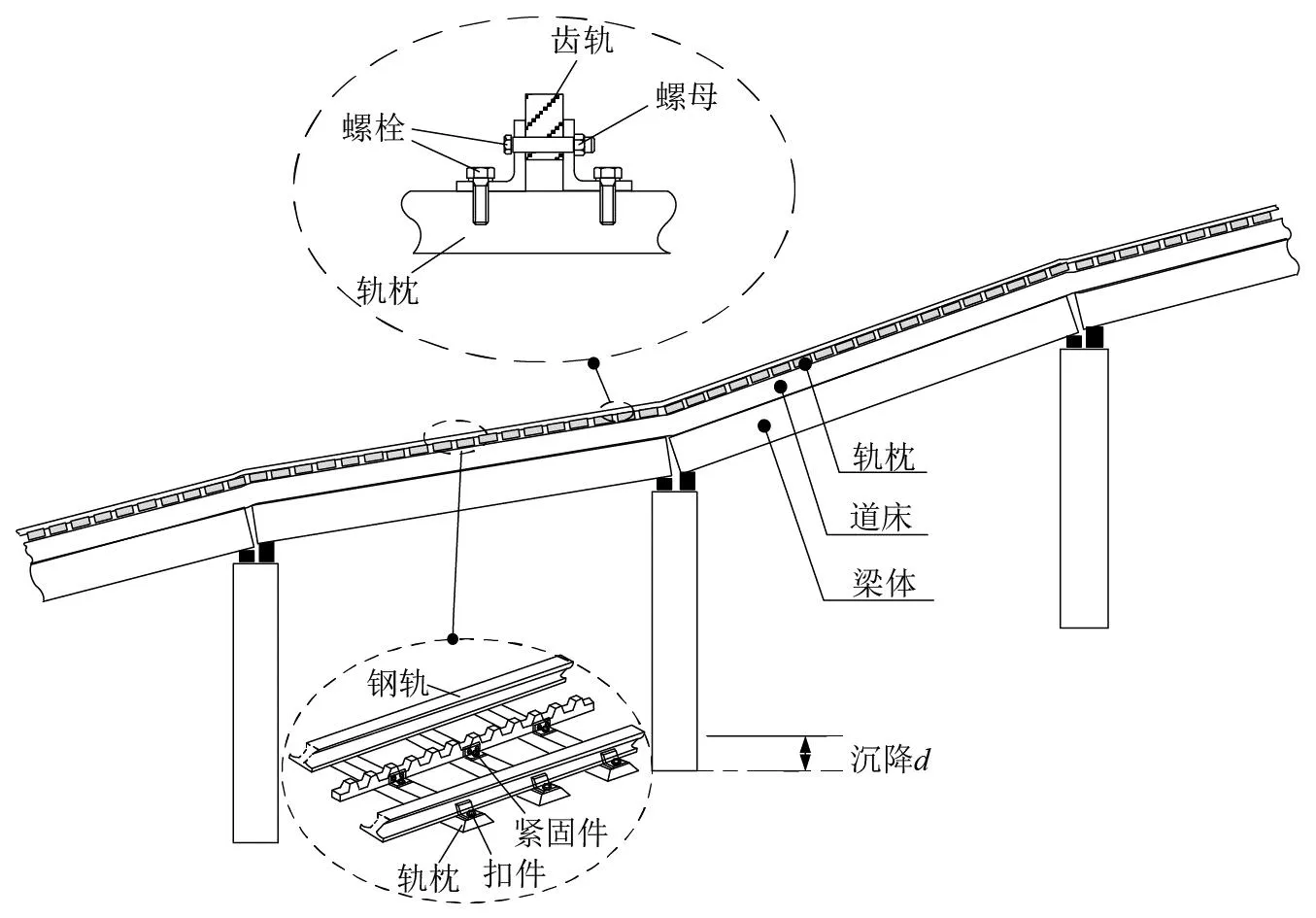
图1 桥墩沉降下齿轨(轨道)-桥梁系统变形示意图Fig.1 Schematic diagram of rack (track)-bridge system deformation under pier settlement

本文以Strub型齿轨车辆为研究对象,考虑钢轨、轨枕和道床颤振效应和车辆的弹性悬挂,建立车辆-齿轨(轨道)-超大坡度桥梁模型,如图2所示。

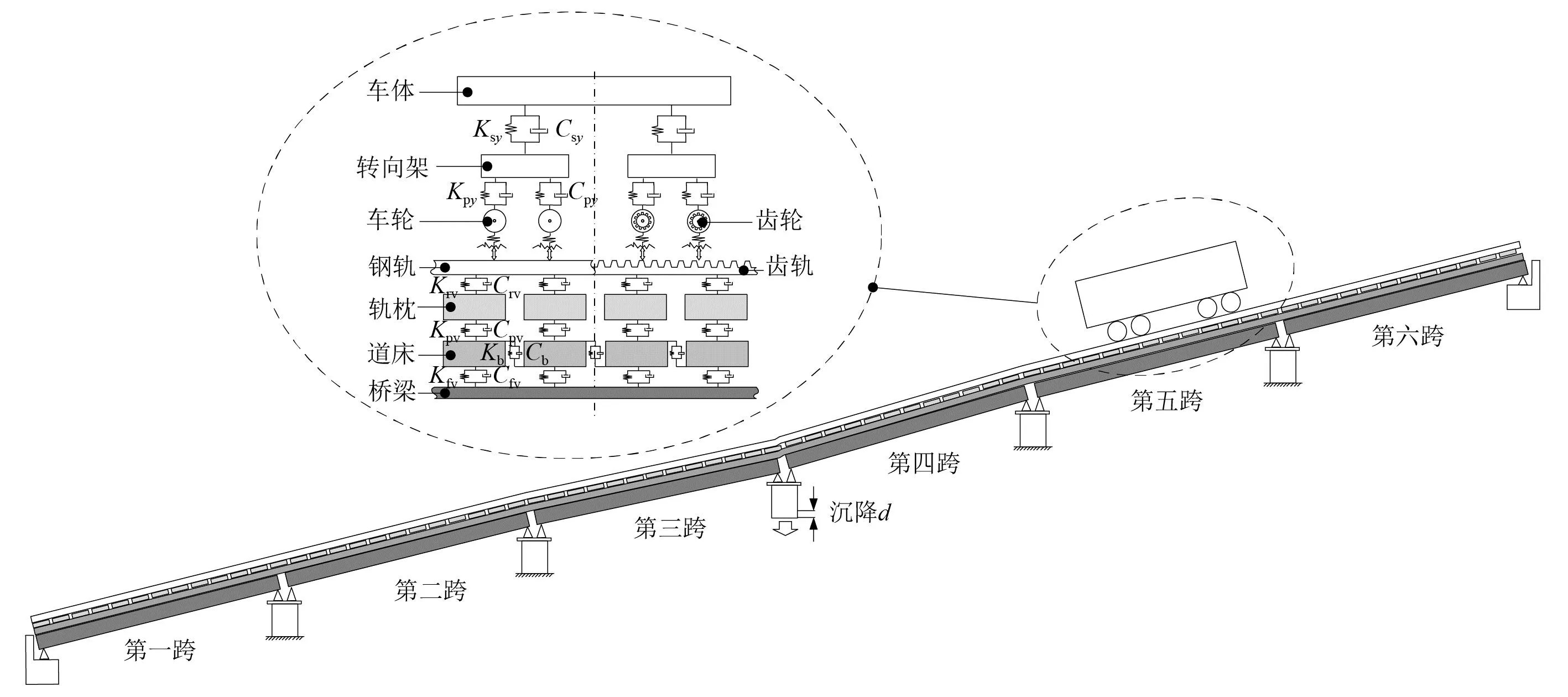
图2 超大坡度Strub型车辆-齿轨(轨道)-桥梁模型示意图Fig.2 Schematic diagram of the model of super-large slope strub vehicle-rack (track)- bridge

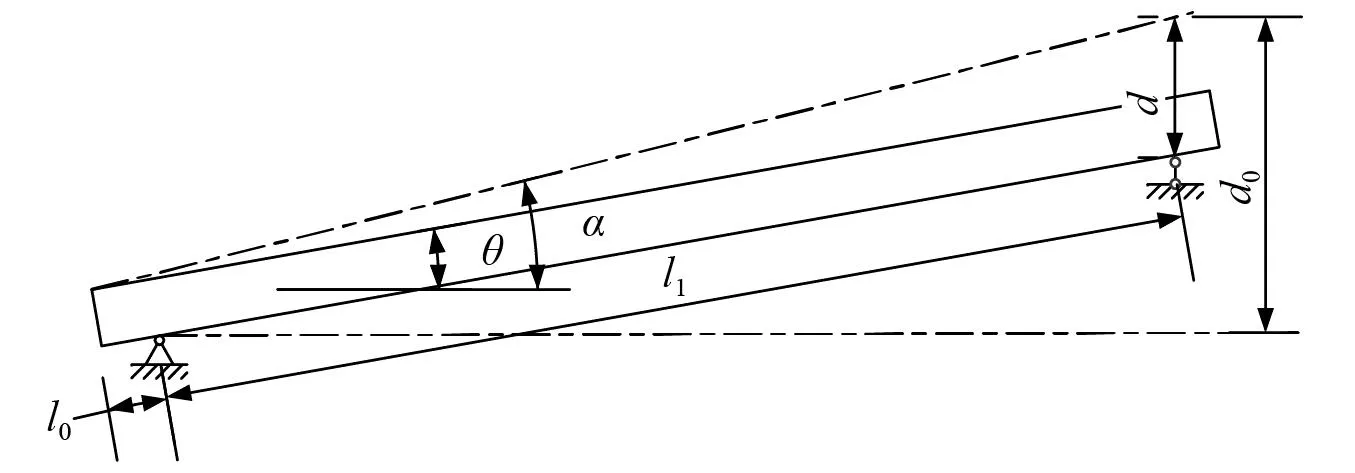
图3 桥梁位移图Fig.3 Bridge deflection diagram

1.1 车辆模型

车辆子系统主要由车体、转向架、轮对和齿轮组成。上述部件被均视作刚体,每个刚体考虑五个方向的自由度,其中车体主要受到二系悬各向力作用、纵向力和横向力;转向架主要受到一系悬挂力和二系悬挂力,齿轮啮合力及摩擦力作用;轮对主要受到来自一系悬挂、齿轮啮合力和轮轨接触力作用;车辆子系统具体动力学方程见陈兆玮的研究。

1.2 齿轨(轨道)模型

有砟轨道模型包括了齿轨(钢轨)、连接件(含扣件)、轨枕、道床等结构,将轨枕视为刚体,齿轨和钢轨视为连续弹性离散点支承上的无限长梁,建立Timoshenko梁模型[22],考虑其扭转和剪切应力。

齿轨垂向振动方程为

(1)

式中:Er为齿轨的弹性模量;ρr和Ar分别为齿轨的截面积和质量密度;Jry为钢轨截面对水平轴的惯性矩;FrVi为齿轨第i个支点的垂向反力;PVj为第j个齿轨作用于齿轨的垂向力;xFi和xPi分别为齿轨第i个支点的x坐标以及第j个齿轮的x坐标。

纵向振动方程为

(2)

式中:Krz为齿轮-齿轨摩擦因数;Gr为齿轨的剪切模量;yrs为齿轨横向距离;xr(t)为齿轮当前位置。

钢轨振动方程与齿轨相似,其垂向和纵向方程分别为

(3)

(4)

式中:Ew和Gw分别为钢轨的杨氏弹性模型和剪切模量;ρw和Aw分别为钢轨的质量密度和截面积;Jwy为钢轨截面对水平轴的惯性矩;FwVi为钢轨第i个支点的垂向反力;PwVj为第j个车轮作用于钢轨的垂向力;xwFi和xwPj分别为钢轨第i个支点的x坐标以及第j个车轮的x坐标;Kwz为轮轨间摩擦因数;yws为钢轨横向距离;xw(t)为车轮当前位置。

轨枕的运动方程为

(5)

左、右轨以及齿轨下道床受力情况相似,其运动方程为

(6)

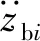
1.3 应力计算

齿轮-齿轨啮合冲击时,齿轨受到齿轮的垂向与纵向载荷,由材料力学理论可以得到齿轨所受轴力FN、剪力Fs以及弯矩M方程为

FN=-Frx

(7)

(8)

(9)

式中:Frx和Frz分别为齿轨纵向和垂向载荷;b为垂向载荷距左端紧固件距离;lf为紧固件间距。

在此基础上,齿轨拉应力σb、齿轨弯曲应力σw以及齿轨紧固件螺栓剪切应力τ可表示为

(10)

(11)

(12)

式中:Ir为横截面对中性轴的惯性矩;y为所求应力点纵坐标;d0为紧固件螺栓直径。

1.4 桥梁模型

利用有限元法[23]建立桥梁结构振动方程

(13)

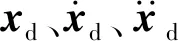
桥梁支座采用弹簧-阻尼单元模拟,支座相邻节点的节点力为

Fi=[Nxi,Qyi,Qzi,Mxi,Myi,Mzi]T

(14)

式中:Nxi为轴向力;Qyi和Qzi为剪力;Mxi为扭矩;Myi和Mzi为弯矩。

在该节点的局部坐标系下,其刚度矩阵可表示为

[K]i=diag[kX,kY,kZ,kRX,kRY,kRZ,
kX,kY,kZ,kRX,kRY,kRZ]

(15)

式中:kX、kY、kZ分别为局部坐标系X轴、Y轴、Z轴方向弹簧系数;kRX、kRY、kRZ分别为绕局部坐标系X轴、Y轴、Z轴方向弹簧系数。

阻尼矩阵为

[C]i=diag[cX,cY,cZ,cRX,cRY,cRZ,
cX,cY,cZ,cRX,cRY,cRZ]

(16)

式中:cX、cY、cZ分别为局部坐标系X轴、Y轴、Z轴方向阻尼系数;cRX、cRY、cRZ分别为绕局部坐标系X轴、Y轴、Z轴方向阻尼系数。

1.5 齿轮-齿轨啮合模型

齿轮-齿轨系统连接是车辆子系统,轨道子系统的纽带之一,也是本文的重点研究对象,建立齿轮-齿轨五自由度模型,考虑齿轮齿条的静态和动态传递误差以及齿侧间隙,齿轮齿条的动态啮合力[24]为

(17)

式中:ki(t)和ci(t)分别为对第i对齿轮的时变刚度和综合阻尼系数;f(t)为其位移函数。

动态摩擦力为

Ffgi(t)=Ffri(t)=λifiFdri(t)

(18)

式中:fi为摩擦因数;λi为摩擦力方向的判断系数。

在此基础上可求得齿轮-齿条啮合的运动方程为

(19)

(20)

(21)

(22)

(23)

式中:Ig为齿轮的转动惯量;Tg为齿轮转矩;θg为齿轮扭转角位移;rbg为齿轮基圆半径;mg和mr分别为齿轮和齿条质量。

1.6 轮轨模型

轮轨力包括轮轨法向力和轮轨蠕滑力。轮轨之间的法向力采用Hertz非线性弹性接触理论计算。则

(24)

式中: δN(t)为轮轨接触点的法向弹性压缩量;G为轮轨接触常数,此处轮对为锥形踏面,取G=4.57R-0.149×10-8m/N2/3。

轮轨之间的蠕滑力按照Kalker线性理论计算,并采用Johnson-Vermeulen理论进行非线性修正,确定蠕滑力后,依据Johnson-Vermeulen理论引入修正系数ε,即可确定轮轨力。确定轮轨力之后,可作为动载荷代入车辆-齿轨(轨道)-桥梁模型,进行后续计算求解,具体过程详见参考文献[25]。

1.7 桥墩沉降模型

在桥墩沉降的作用下,相邻的两跨梁体发生竖向位移,轨枕随之发生位移,扣件也在其作用下移动,进而导致钢轨和齿轨受到扣件力的作用,发生竖向位移。由上述分析可知,只有在与沉降墩台相邻处的桥梁会发生位移。

设桥梁的坡度为α,此时位于第i跨桥梁的M点的纵坐标为

(25)

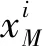
d0=l1·sinα

(26)

当该桥墩发生距离为d的沉降时,该点的纵坐标为

(27)

故,在桥墩沉降量为d时,此点发生的垂向位移量为

(28)

同理可得,第i+1跨桥梁上某一点d垂向位移量为

(29)

所以,对应扣件位置处的桥梁位移矩阵可表示为

Zb=D·d

(30)

式中,D为沉降量对桥梁位移的影响关系矩阵。

根据简支梁挠度公式, 齿轨上任一点的变形均可以表达为所有扣件力的函数, 该函数即桥墩沉降与齿轨变形的映射关系

(31)

其中,

(32)

式中:xr为观测点距离齿轨左侧的距离; INT(x)为对x取整,故Nf(xr)为xr长度范围内紧固件数目。

将依据上述内容所得到的齿轨上扣件力的函数,代入建立的车辆-齿轨(轨道)-桥梁系统方程中,即可求解桥墩沉降下的齿轨铁路动力学方程。

作者开展了齿轨铁路现场试验,对上述动力学模型的有效性进行了验证,详细验证过程见赵冠闯等的研究。

2 桥墩沉降下齿轨-桥梁系统适应性及安全性

采用第1章建立的模型,轨道不平顺采用美国五级谱,研究Strub型齿轨铁路在不同桥墩沉降量下的齿轨变形,齿轨振动以及螺栓剪切应力等关键指标,在此基础上对该系统的适应性和安全性进行分析评估。模型主要动力学参数如表1所示,桥梁截面如图4所示。

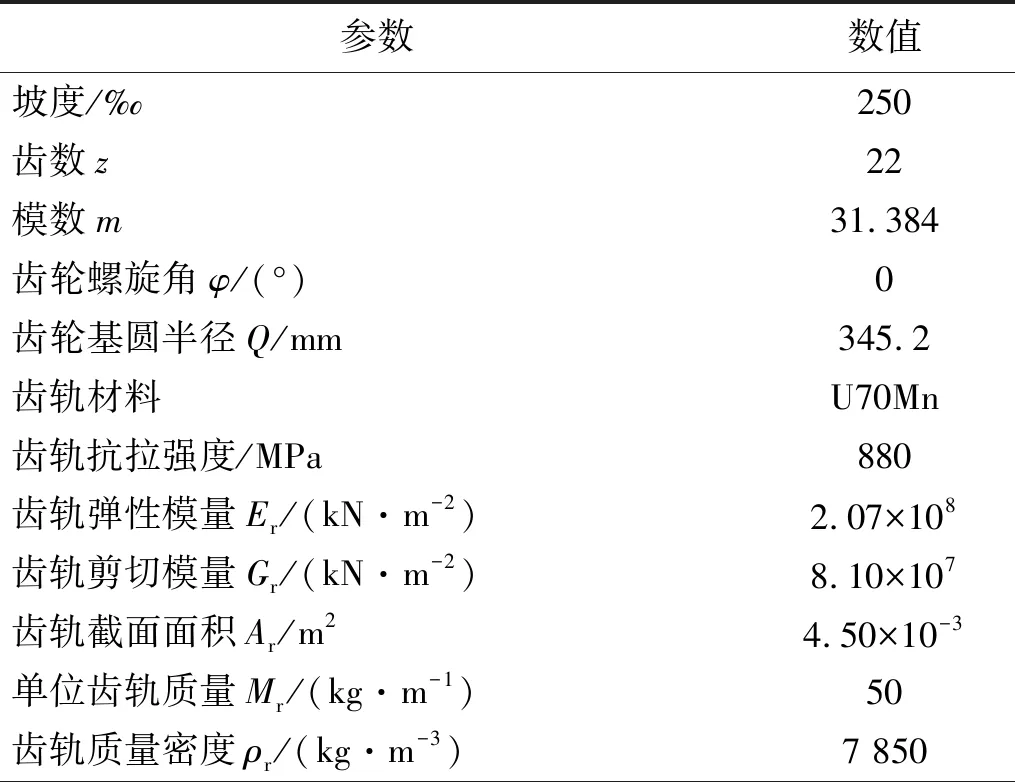
表1 车辆-齿轨(轨道)-桥梁模型参数Tab.1 Parameters of vehicle-rack-bridge model

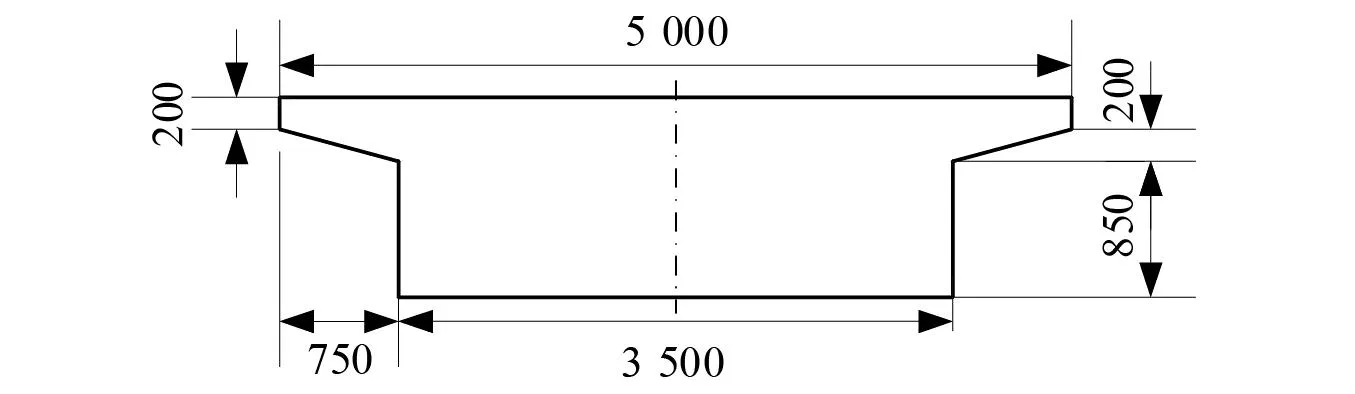
图4 桥梁截面图(cm)Fig.4 Bridge section(cm)

桥梁跨度取25 m,为消除边界条件对结果的影响,本文采用6跨桥开展研究,桥墩沉降量分别取2 mm、4 mm、6 mm、8 mm、10 mm五个等级,在中间桥墩处分别施加上述五个沉降量开展计算,齿轨变形量如图5所示。由图5可知,桥墩沉降对齿轨变形具有显著影响,沉降桥墩及其相邻两跨桥梁桥墩位置处都会发生变形,桥梁最大变形出现位置在施加位移的墩台处,并在最大变形处附近出现过渡曲线。同时,相邻两跨梁体,齿轨均出现上翘现象,且齿轨的变形量随着桥墩沉降量的增加而增加。

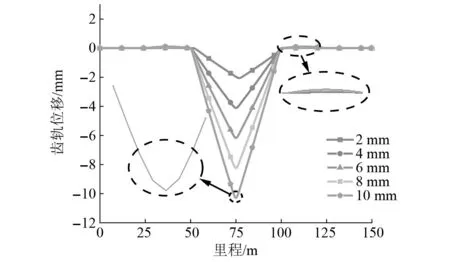
图5 不同桥墩沉降量下齿轨位移图Fig.5 Rack displacement diagram under different pier settlement

在桥墩沉降作用下,齿轨会产生拉压应力,进而导致齿轨与轨枕之间连接螺栓产生剪切应力和弯曲应力。垂向和纵向扣件力(图1中水平向螺栓,下同)变化如图6、图7所示,桥墩沉降对垂纵向扣件力影响较大的位置也发生在沉降桥墩和相邻桥墩处,在沉降桥墩处出现垂向和纵向扣件力峰值,此时螺栓所受垂向剪切应力为7.9 MPa,纵向剪切应力为98 MPa,均低于螺栓许用应力;齿轨所受拉应力最大值为10.67 MPa,远低于齿轨抗拉强度。不同沉降量下齿轨拉应力与螺栓剪切应力峰值如图8、图9所示,因此,在上述沉降量下,连接螺栓与齿轨强度满足使用要求。

图6 不同桥墩沉降量下垂向扣件力Fig.6 Vertical fastener force under different pier settlement

图7 不同桥墩沉降量下纵向扣件力Fig.7 Longitudinal fastener force under different pier settlement

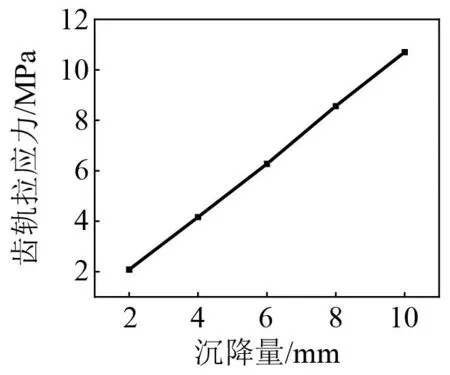
图8 不同桥墩沉降量下齿轨拉应力Fig.8 Tension stress of rack under different pier settlement

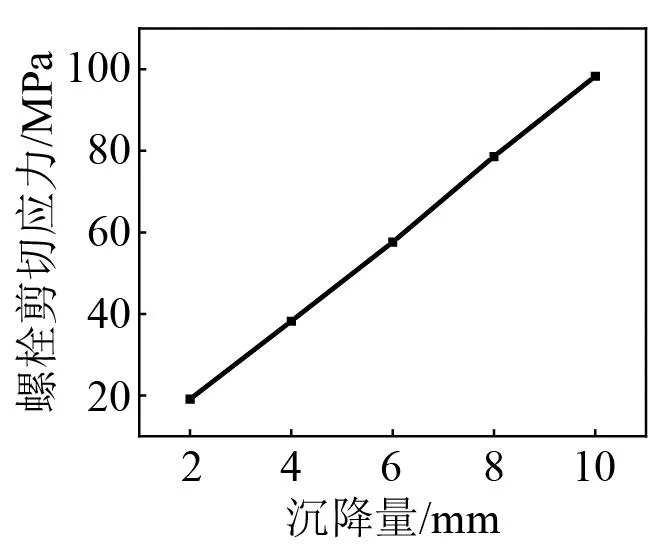
图9 不同桥墩沉降量下螺栓剪切应力Fig.9 Bolt shear stress under different pier settlement

3 多荷载综合作用下桥梁-齿轨系统适应性及安全性

详细考虑齿轮齿轨非线性动态啮合冲击、轮轨间非线性动态接触作用,轨道不平顺和桥墩沉降等复杂因素,进一步研究多荷载综合作用下的车辆-齿轨-桥梁系统。

图10、图11为纵向轮轨力及其振动频率,垂向轮轨力约为29～36 kN,振动主频在2～4 Hz,在2 Hz和4 Hz处有明显峰值,纵向轮轨力较小,峰值约为10 kN,振动主频在1 Hz左右。由于垂纵向轮轨力波形相仿,所以此处只展示纵向轮轨力在时域和频域上的波形。图12、图13为纵向啮合力及其振动频率,垂向啮合力幅值仅为0～0.13 kN,对系统影响较小,而纵向啮合力较大,幅值近125 kN,垂向和纵向啮合力的振动主频均较为平稳,无明显主频。图14为齿轮垂向偏移量,由图14可知,桥墩沉降对齿轮垂向偏移量影响较小,基本不会影响齿轮-齿条啮合。

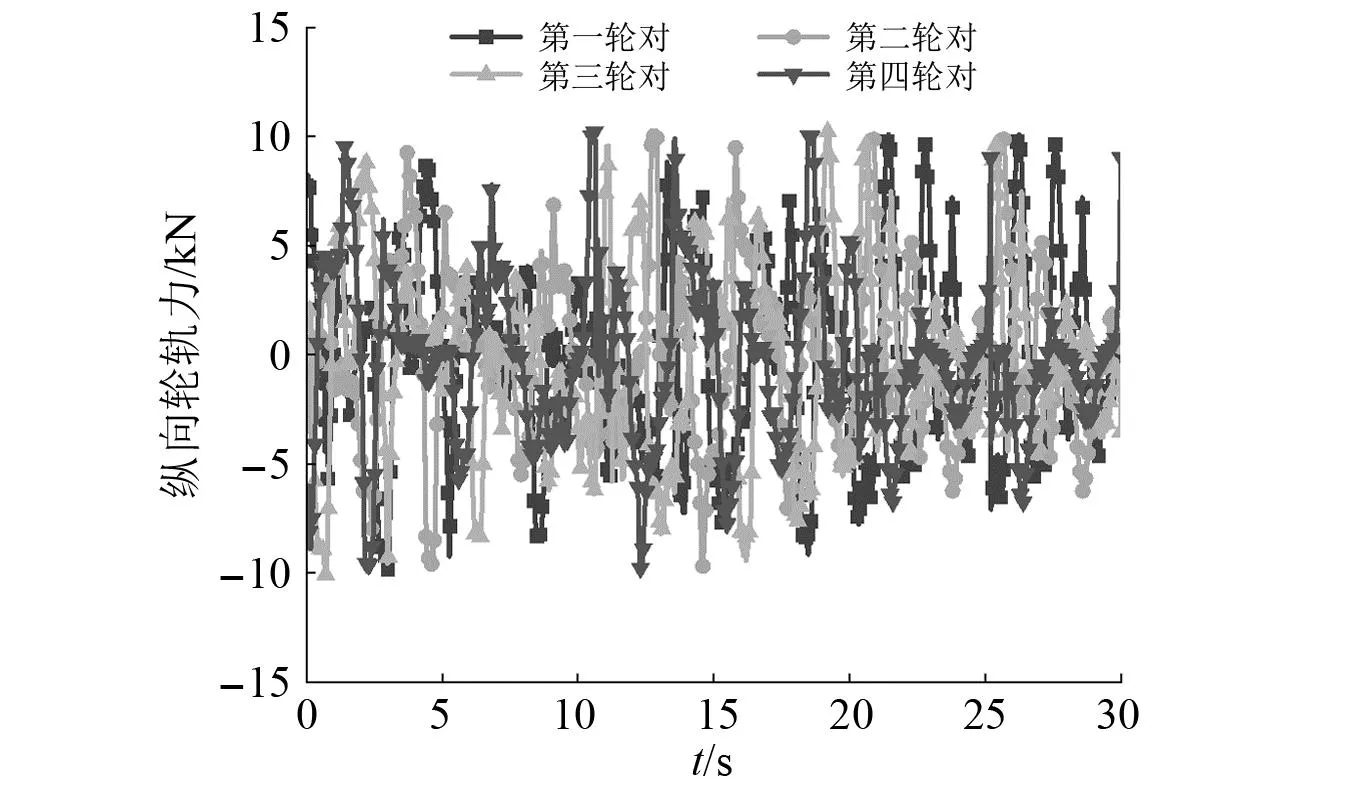
图10 纵向轮轨力Fig.10 Longitudinal wheel-rail force

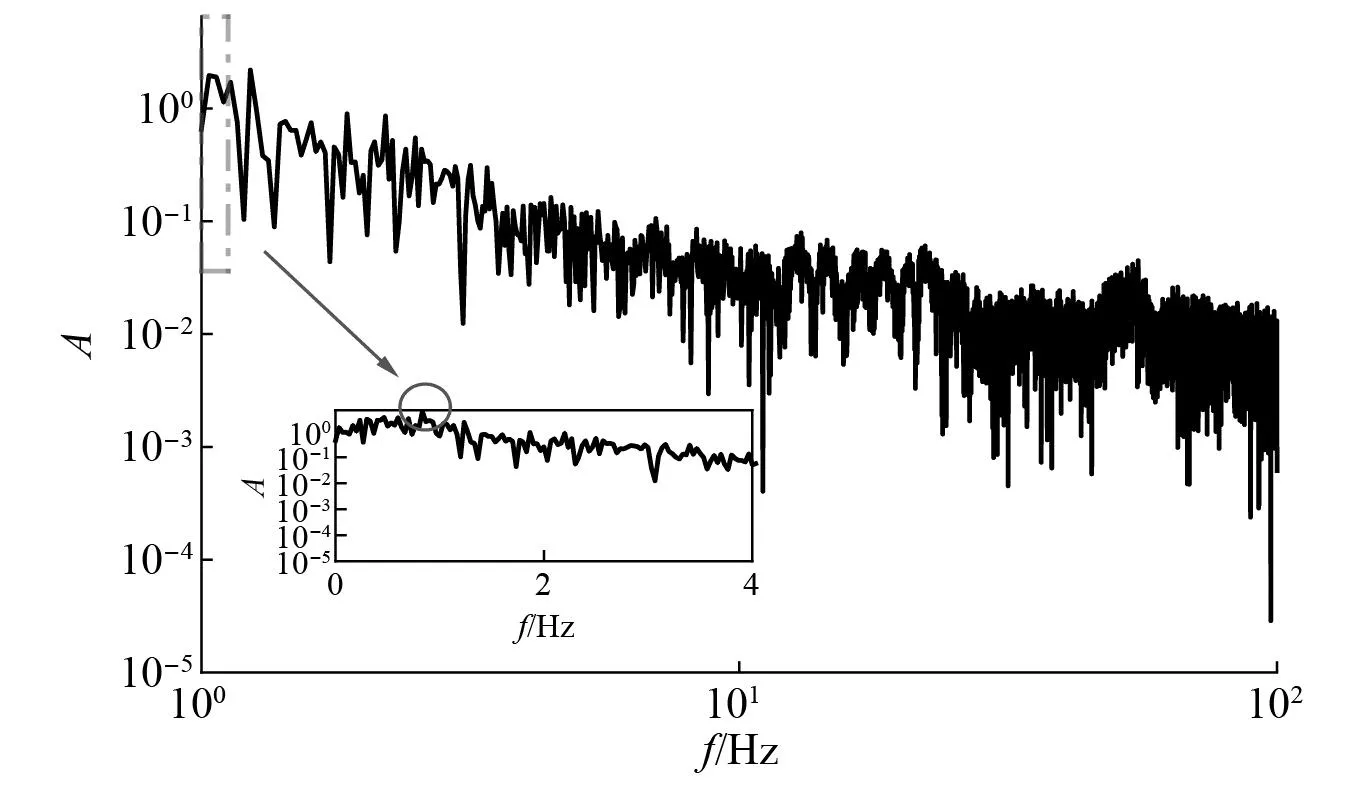
图11 纵向轮轨力振动频谱Fig.11 Longitudinal wheel-rail force vibration frequency

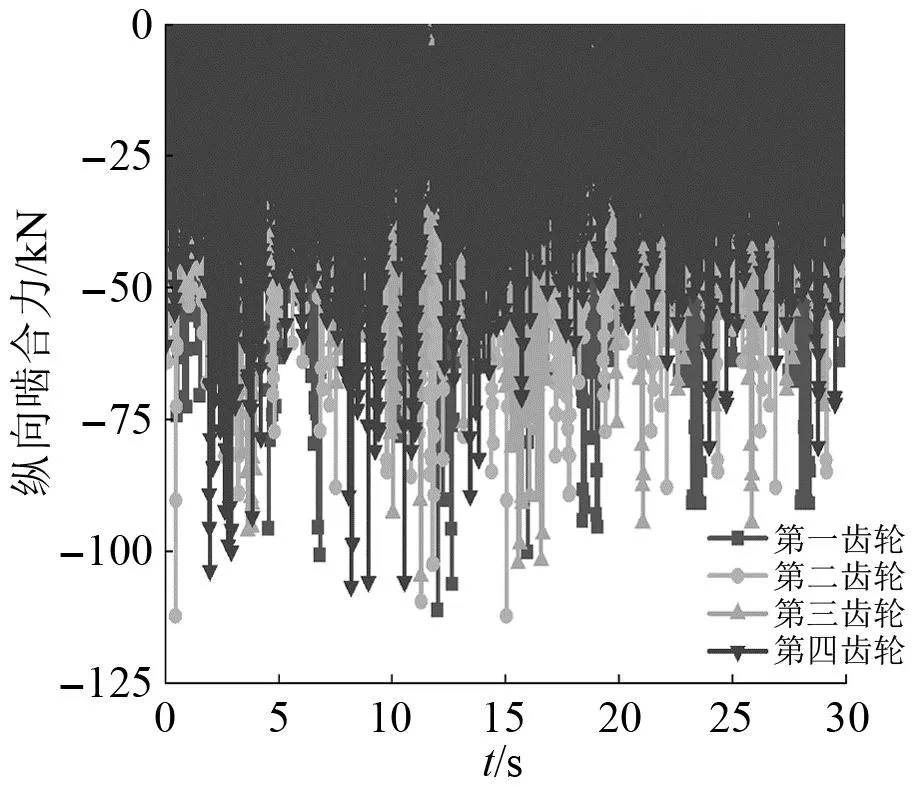
图12 纵向齿轮-齿轨啮合力Fig.12 Longitudinal gear-rack meshing force

图13 纵向啮合力振动频谱Fig.13 Vibration frequency of longitudinal meshing force

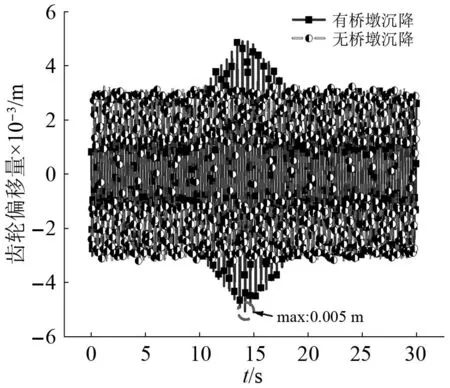
图14 齿轮偏移量Fig.14 Deviation of the gear

图15、图16为桥墩沉降10 mm下齿轨垂/纵向变形量,在多荷载耦合作用下,齿轨变形量仍集中在沉降桥墩及相邻两跨桥梁墩台处,同时,桥墩沉降对该系统影响较为显著,齿轮齿轨啮合力和轮轨力对齿轨变形量影响较小。图17、图18为不同桥墩沉降量下齿轨垂纵向变形量最大值,桥墩沉降量与齿轨变形量呈正相关,最大变形量出现在桥墩沉降处,相邻桥墩处仍出现轻微上翘现象。

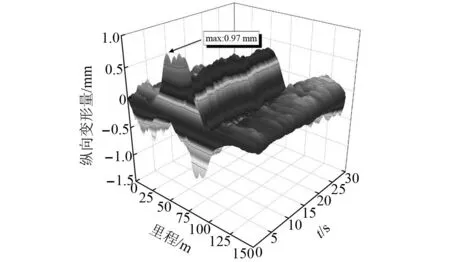
图15 桥墩沉降10 mm下齿轨纵向变形量Fig.15 Longitudinal deformation of rack under pier settlement of 10 mm

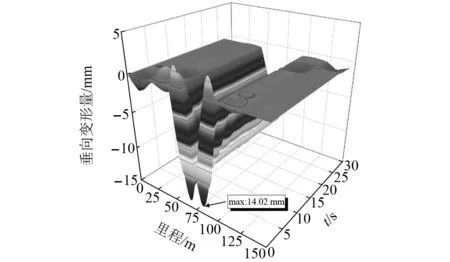
图16 桥墩沉降10 mm下齿轨垂向变形量Fig.16 Vertical deformation of rack under 10 mm pier settlement

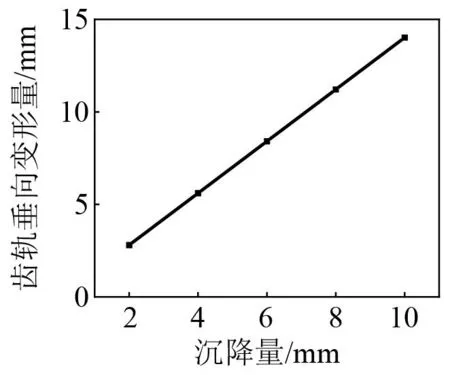
图18 不同桥墩沉降量下齿轨垂向变形量最大值Fig.18 Maximum vertical deformation of rack under different pier settlement

图19～图22为桥墩沉降10 mm下齿轨垂/纵向加速度,图23为不同桥墩沉降量下各桥梁跨中位置处齿轨加速度最大值,由图23可知,桥梁跨中位置处的齿轨加速度对桥墩沉降量的变化并不敏感,这是由于齿轨(轨道)存在使得桥墩沉降的附加线形光滑,啮合力和轮轨力不会产生较大附加冲击。同时,该处纵向加速度明显大于垂向加速度,最大纵向加速度为140.24 m/s2,最大垂向加速度为8.63 m/s2,均发生在第一跨桥梁跨中处。齿轨纵向振动主频位于70～80 Hz,垂向振动主频位于70～75 Hz与95～97 Hz。

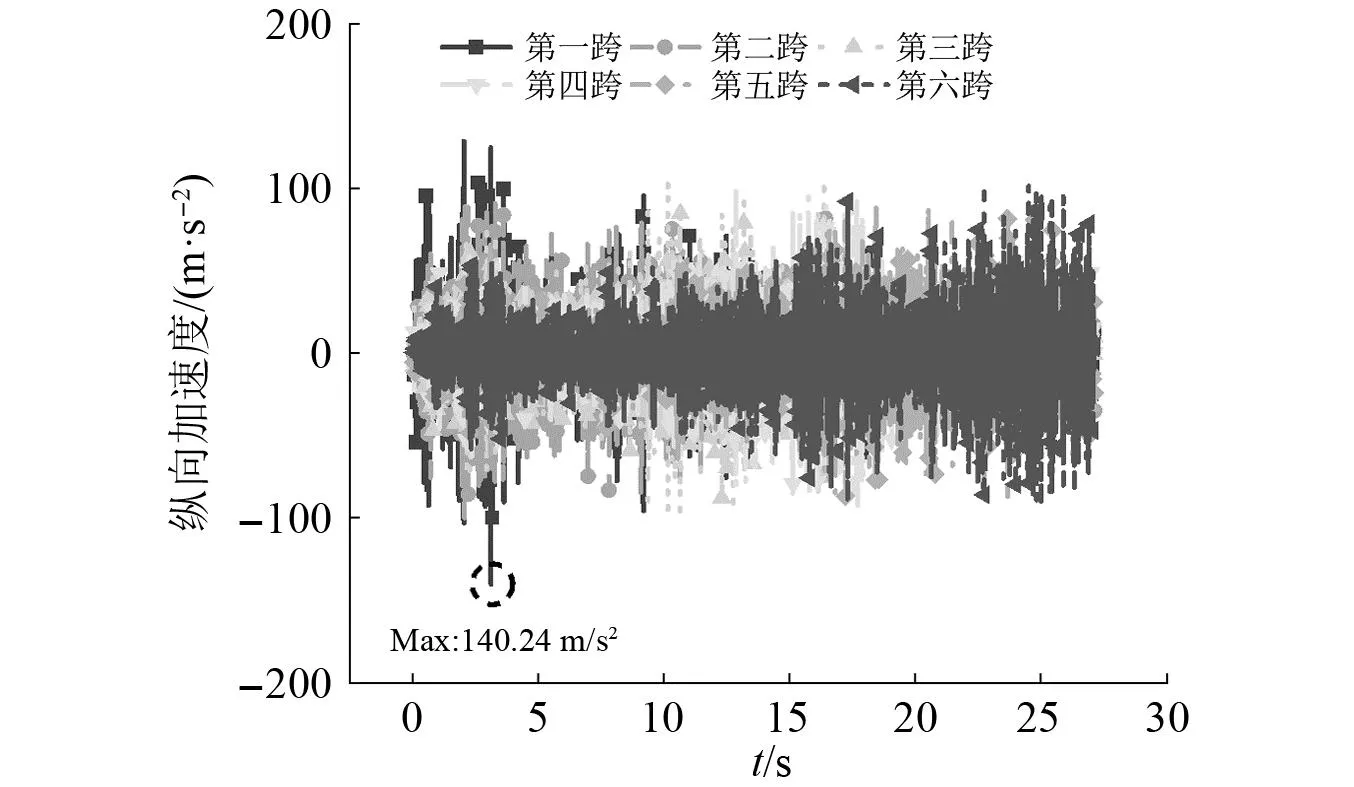
图19 桥墩沉降10 mm下齿轨纵向加速度Fig.19 Longitudinal acceleration of rackunder 10 mm pier settlement

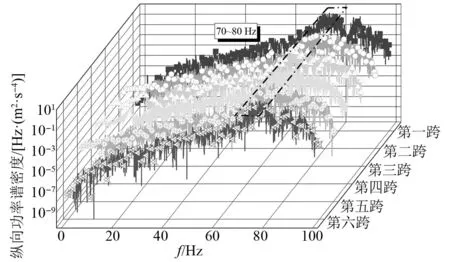
图20 桥墩沉降10 mm下齿轨纵向加速度频谱密度Fig.20 Frequency spectrum density of longitudinal acceleration of rack under 10 mm pier settlement

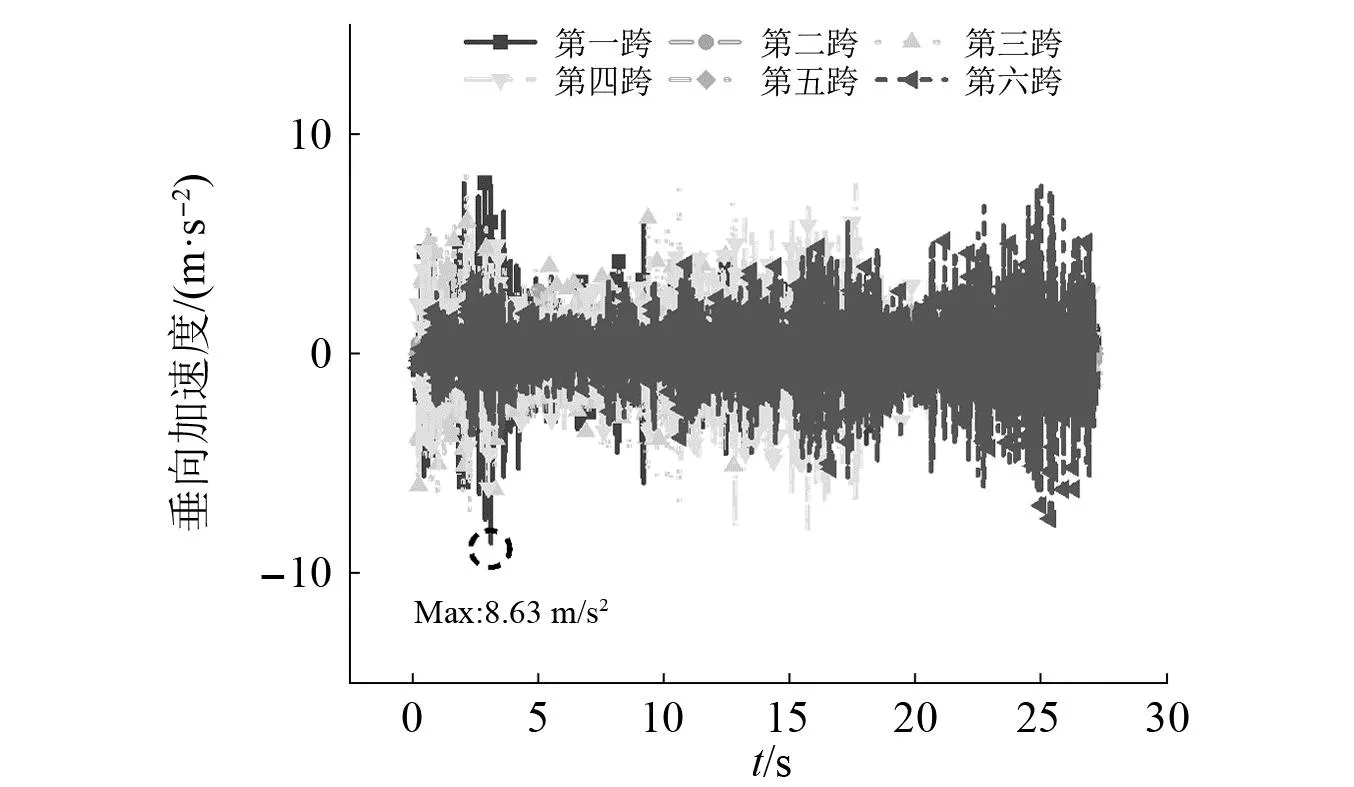
图21 桥墩沉降10 mm下齿轨垂向加速度Fig.21 Vertical acceleration of rack under 10 mm pier settlement

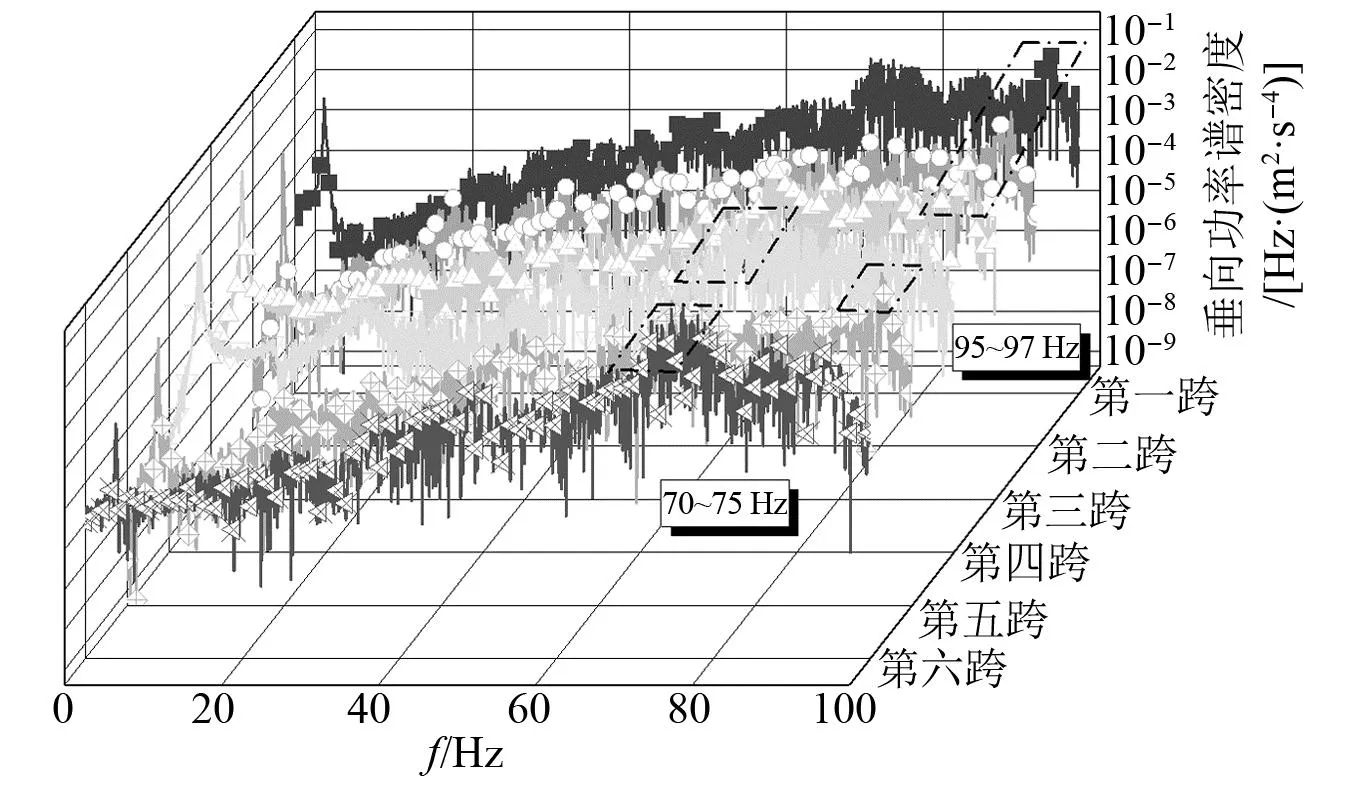
图22 桥墩沉降10 mm下齿轨垂向加速度频谱密度Fig.22 Spectrum density of vertical acceleration of rack under 10 mm pier settlement

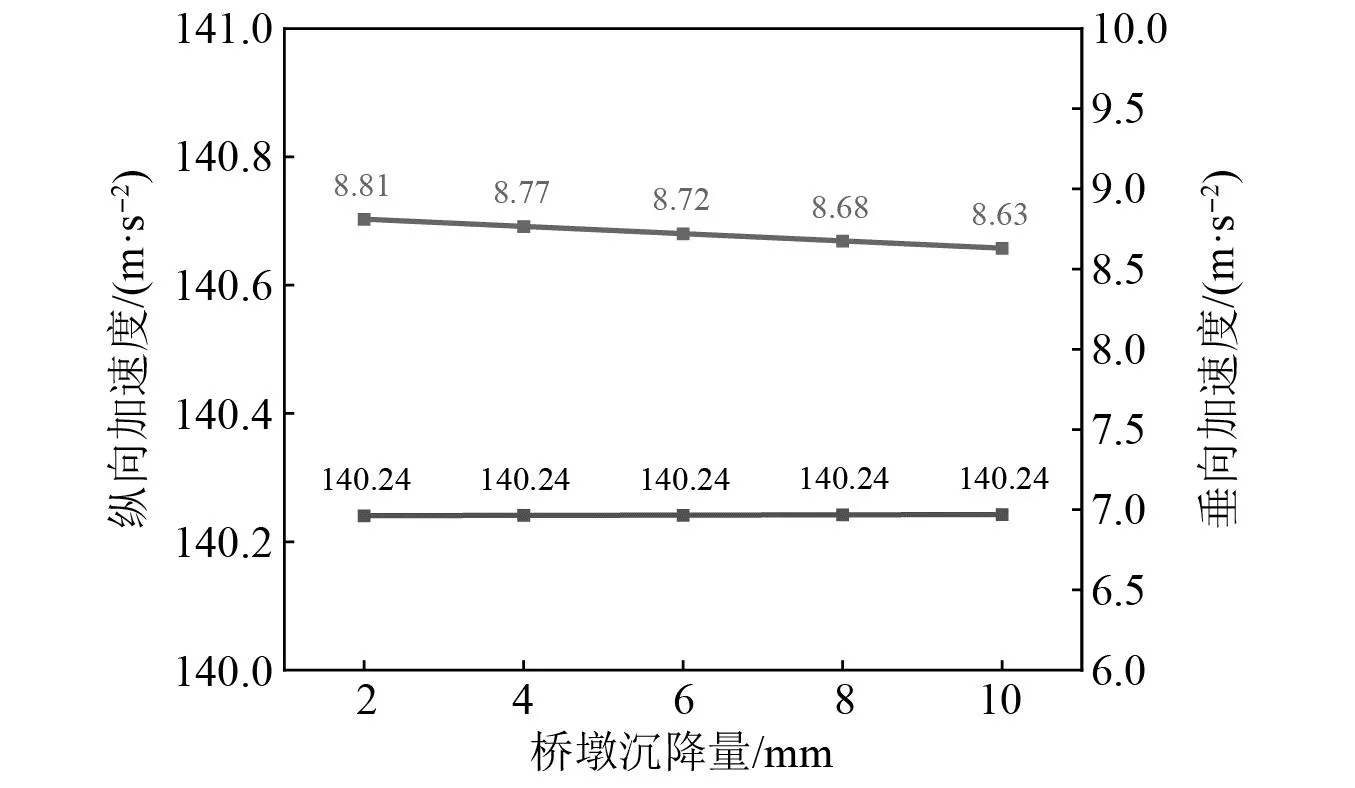
图23 不同沉降量下桥梁跨中位置处齿轨加速度最大值Fig.23 Maximum acceleration of rack at mid-span position of bridge under different settlement

图24、图25为桥墩沉降10 mm下垂纵向齿轨力变化图,图中结果表明不同沉降量下齿轨力的峰值均出现在沉降桥墩处。图26、图27表示不同沉降量下垂纵向齿轨力的峰值,桥墩沉降量与齿轨力呈正相关,且沉降量对齿轨纵向力的影响逐渐增大。这是由于桥墩沉降导致相邻梁体发生竖向位移,进而使得齿轨和钢轨发生竖向变形。而齿轨许用变形量较小,导致齿轨力随着桥墩沉降量的增大而迅速增加,从而使得螺栓应力增大。若齿轨力过大,可能造成齿轨拉压应力及齿轨连接螺栓剪切应力过大,甚至导致齿轨局部损伤或连接螺栓断裂,严重威胁行车安全,故对齿轨拉压应力和螺栓剪切应力进行研究。

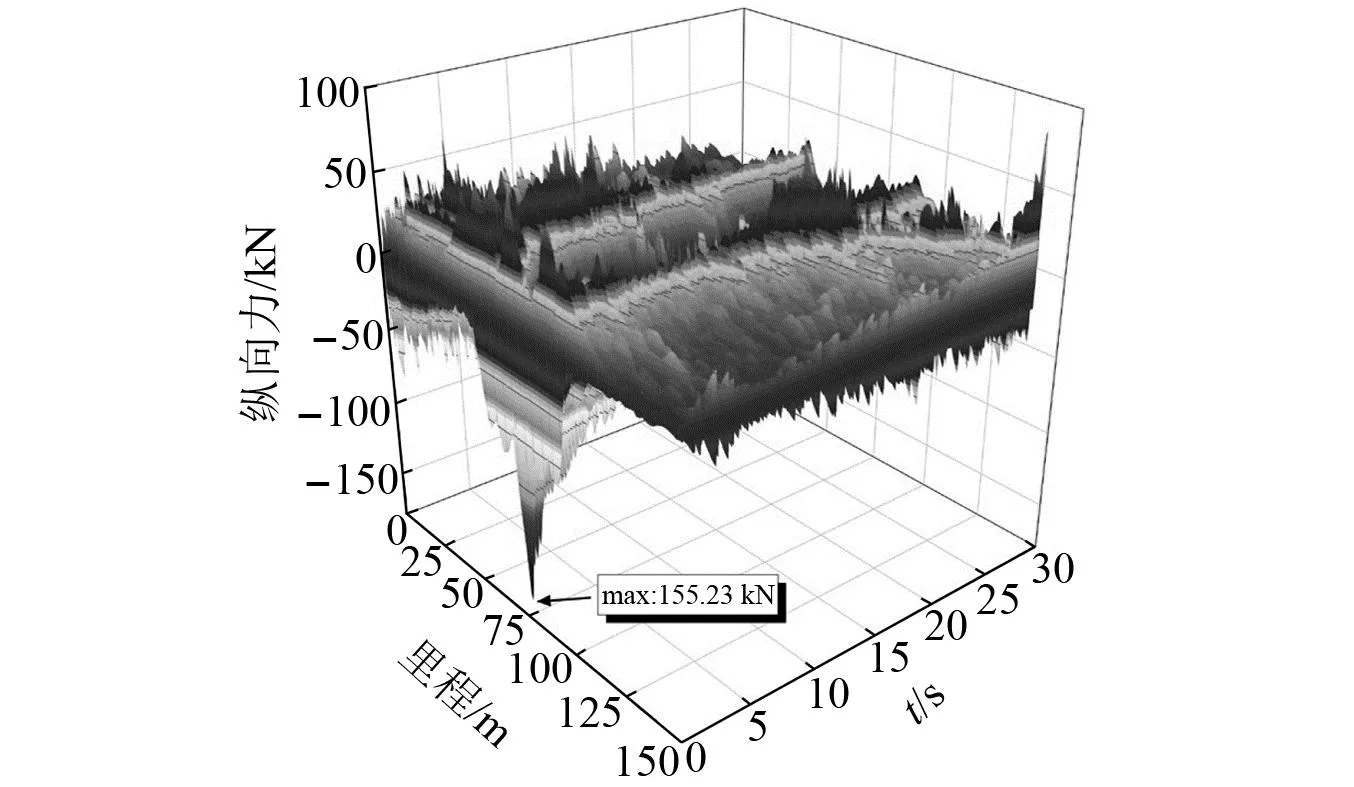
图24 桥墩沉降10 mm下齿轨纵向力Fig.24 Longitudinal force of rack under pier settlement of 10 mm

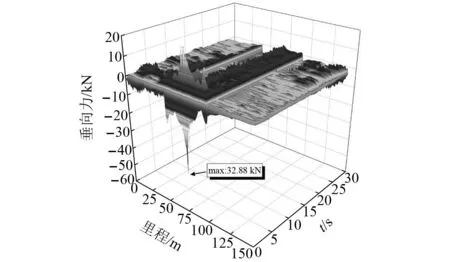
图25 桥墩沉降10 mm下齿轨垂向力Fig.25 Vertical force of rack under pier settlement of 10 mm

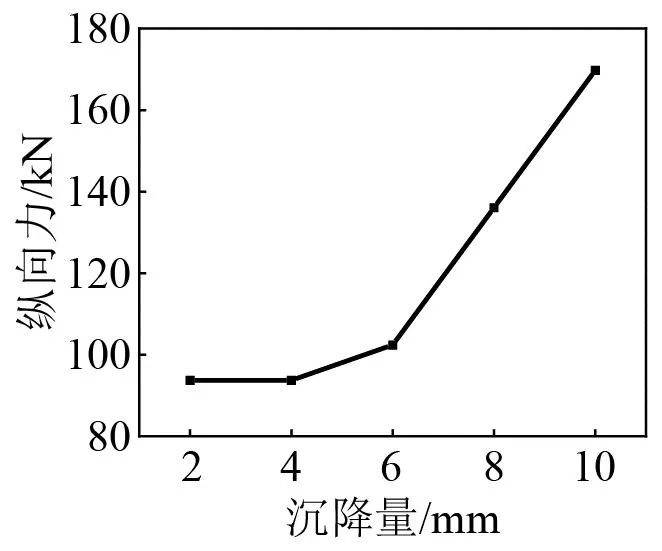
图26 不同桥墩沉降量下齿轨纵向力最大值Fig.26 Maximum longitudinal force of rack under different pier settlement

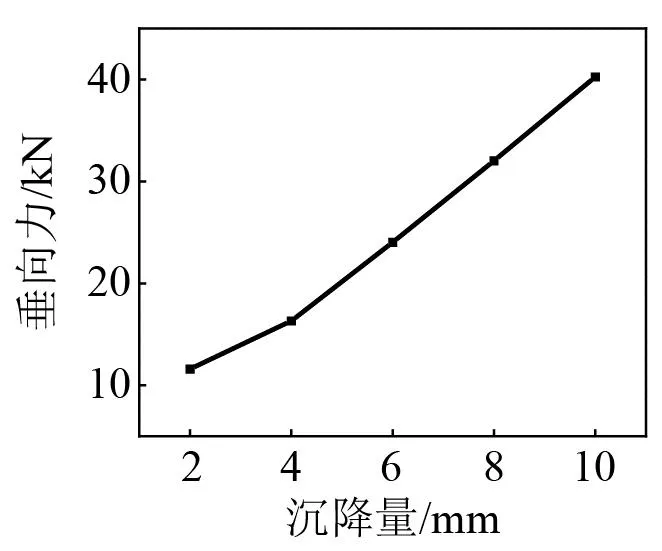
图27 不同桥墩沉降量下齿轨垂向力最大值Fig.27 Maximum vertical force of rack under different pier settlement

图28为不同沉降量下齿轨拉应力最大值,图29表示不同沉降量下连接螺栓剪切应力最大值。齿轨拉应力最大值为38.77 MPa,齿轨的抗拉强度为880 MPa,计算所得结果远低于该值,故不予讨论。螺栓的剪切应力最大值为346.43 MPa,螺栓剪切强度为235 MPa,通过计算,在沉降量为6.76 mm时,螺栓剪切应力已达螺栓许用剪切应力值(235 MPa),故螺栓在使用过程中会发生剪断等失效,严重威胁行车安全。上述计算结果表明,齿轨与轨枕之间通过螺栓进行连接无法满足相关标准的强度安全,因此,建议将齿轨与轨枕之间的连接件由螺栓更换为弹性扣件,以减小由桥墩沉降导致的齿轨变形量,从而降低齿轨应力,增强该系统的适应性,保证行车安全。

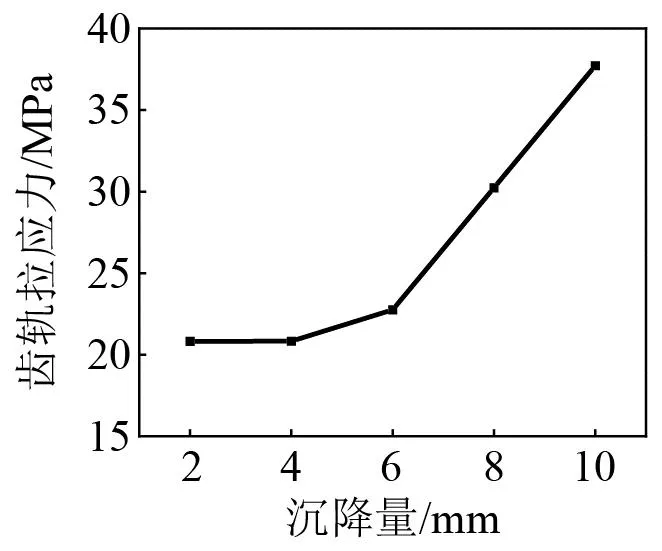
图28 不同桥墩沉降量下齿轨拉应力最大值Fig.28 Maximum tensile stress of rack under different pier settlement

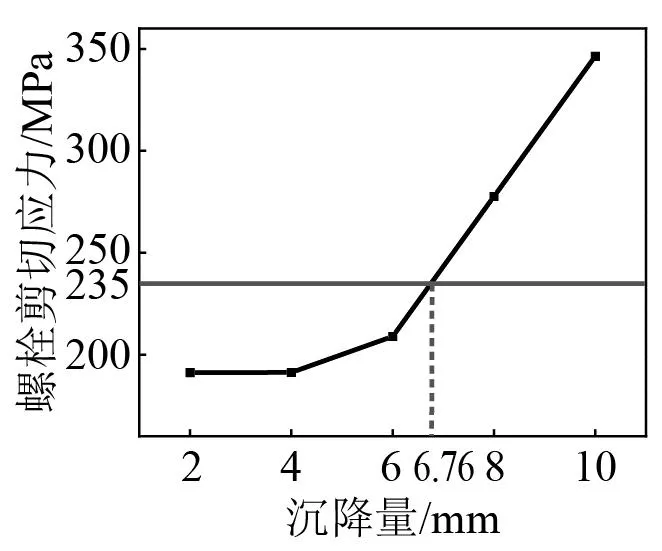
图29 不同桥墩沉降量下螺栓剪切应力最大值Fig.29 Maximum value of bolt shear stress under different pier settlement

4 结 论

本文基于列车-轨道-桥梁动力相互作用理论,建立了桥墩沉降下齿轨车辆-齿轨(轨道)-超大坡度桥梁系统耦合动力学模型,研究了列车通过时桥墩沉降对齿轨垂/纵向变形、应力、加速度以及连接螺栓应力的影响,最终提出山区大坡度齿轨铁路桥墩沉降安全控制值。通过研究得到以下结论:

(1) 桥墩沉降单独作用下,齿轨变形主要集中在沉降桥墩及其相邻桥墩处,最大变形量出现在沉降桥墩处,并在相邻两跨桥墩处齿轨出现上翘现象,且齿轨变形量随着墩台沉降量的增大而增大。在本文计算条件下,单独由桥墩沉降引起的螺栓和齿轨应力均未超过标准范围。

(2) 在桥墩沉降、齿轮齿轨动态啮合、轮轨动态接触等多荷载耦合作用下,齿轨变形主要发生在沉降桥墩和相邻桥墩处,桥墩沉降量对齿轨垂向变形量的影响较为显著。

(3) 由于桥墩沉降产生的附加曲线线性光滑,所以该荷载不会引起较大的附加冲击,因此在多荷载耦合作用下,桥梁跨中位置处的齿轨振动主要由齿轮齿轨非线性啮合行为和轮轨非线性接触行为导致,跨中纵向加速度最大值出现在第一跨桥梁的跨中位置,为140.24 m/s2,垂向加速度最大值为8.81 m/s2,纵向振动主频位于70～75 Hz,垂向振动主频为70～75 Hz和95～97 Hz。

(4) 当桥墩沉降量为6.76 mm时,连接螺栓剪切应力达到其许用剪切强度235 MPa,连接螺栓极有可能发生断裂,严重威胁行车安全。因此,就齿轨车辆运行安全性而言,建议山区齿轨铁路桥墩沉降控制在 6.76 mm内。

齿轨车辆虽具有良好的爬坡性能,但仍存在运行速度低、运行振动较大等问题。所以,后续建成相关齿轨线路后,应着重关注车辆加速度、紧固件加速度、齿轨应力应变、疲劳性、齿轮偏移量和齿轮时变啮合刚度等相关参数,从而保证车辆运行平稳性和安全性。同时,本文仅分析了桥墩沉降对齿轨结构的影响,为使本研究更加完善,后续将对不同车速和线路坡度下桥墩沉降对齿轨结构的影响进行分析。