三枕捣固作业过程中道砟细观运动及能量演变分析

张智海，肖 宏，崔旭浩，刘光鹏

(1.北京交通大学土木建筑工程学院，北京 100044；2.北京交通大学轨道工程北京市重点实验室，北京 100044)

在长期自然环境影响及高速列车动荷载作用下散体道床易发生道砟磨耗、破碎，改变道床级配和道砟的工作性能，使道床产生不均匀沉降，改变线路几何形位，降低线路平顺性，影响列车运营品质[1-3]。为保持线路的平顺性和安全性，需不断的进行养护维修作业[4-5]。目前，采用大型捣固车对线路进行定期或不定期的维修作业(简称大机捣固)已成为消除有砟轨道不平顺病害的有效手段[6]。但大型捣固作业车种类繁多、参数及作业工序多样，现场捣固作业质量难以控制。不合理的大机捣固作业方式不仅不能达到整正线路几何形位、提高道床密实程度的目的，还会造成道床越捣越松、道砟颗粒破碎等负面影响，降低散体道床的服役寿命，增加工务养护维护成本[7-8]。因此，为探明有砟道床捣固密实机理，提高捣固作业质量，需开展大机捣固作业对有砟道床的作用效应影响研究，从细观角度揭示捣固作业过程中道砟颗粒运动力学机制。

近年来，诸多学者主要利用物理试验和数值模拟两种手段来研究大机捣固作业对有砟道床宏细观力学特性的影响。在物理试验研究方面，LIU等[9]、王卫东等[10]和KOC 等[11]开展了现场单枕、双枕捣固作业前后道床纵横向阻力试验，分析了捣固作业次数与道床纵横向阻力间的内在联系，验证了利用捣固车来测量道床纵横向阻力的可靠性，研究结果表明：道床阻力随着捣固次数的增加，呈先增大后减小的变化趋势。KUMARA等[12]和MCDOWELL 等[13]借助室内缩尺试验平台，研究了不同脏污状态道砟试样在捣固作业后的沉降特性，结果表明：脏污道床捣固作业计划与脏污率密切相关。AINGARAN 等[14]和PADERNO 等[15]借助室内试验来模拟捣固作业过程中枕下道砟的受力，分析了捣固作业对道床劣化及长期服役性能的影响。PRZYBYŁOWICZ 等[16]通过室内试验，探究了垂直捣固法和侧向捣固法的差异性，结果表明：侧向捣固法更有利于提高枕端道砟密实度。综合分析可知，以上试验研究主要以室内试验为主，缺乏大量现场试验研究。仅有的现场试验主要关注捣固作业对道床阻力特性的影响，未从细观角度揭示捣镐与道砟之间相互作用机制，且现场试验对象为单枕、双枕捣固作业车，并未涉及三枕捣固作业车。与单枕、双枕捣固作业相比，三枕捣固作业扰动范围更大，道床部分区域振动强度更高，对道床的宏细观力学状态影响更为显著，因此现有的单枕、双枕捣固作业的研究无法反映三枕捣固车对有砟道床的作用效应。

在数值模拟方面，SHI 等[17]建立了较为精细的双枕捣固装置-有砟道床耦合分析模型，分析了捣固作业参数对道床力学行为的影响，但该模型在模拟捣镐运动时并未考虑道砟对捣镐的非线性阻力特性。SAUSSINE 等[18]和ZHOU 等[19]利用离散单元法建立了道砟箱局部捣固作业模型，探究了捣固作业参数与道床密实度间的内在联系，研究结果表明：夹持力和捣镐振动频率对捣固作业后道床密实度影响较大。WANG 等[20]建立了小型捣固设备与有砟道床耦合仿真模型，分析了道砟在捣固作业过程中的振动响应特性。由以上数值仿真研究可知，捣固作业仿真模型局限于双枕及小型捣固设备，并未涉及DWL-48 型捣固稳定车的三枕捣固装置(09-3X)-有砟道床耦合分析模型。由此可见，目前针对有砟道床捣固作业的机理研究尚落后于大型捣固养维修设备在工程实际中的应用，尤其是在高效率、高质量的三枕捣固作业方面，鲜有相关文献报道。此外，模拟研究主要针对捣固作业参数，并未从细观角度探究捣固作业过程中道砟的细观运动特征，无法从本质上揭示捣固密实工作原理及力学机制。

针对上述研究中的不足之处，本文结合DWL-48连续走行捣固稳定车三枕捣固装置的实际动态作业过程，率先建立了三枕捣固装置-轨排-有砟道床多层多介质、多尺度精细化耦合仿真模型，分析了三枕捣固作业过程中道砟颗粒移动、旋转及能量演变规律。从细观角度揭示了捣固作业过程中捣镐与道砟间相互作用，探明了捣固作业过程中道砟颗粒的运动形式及密实过程，加深了对三枕捣固作业过程中道砟细观运动特征的认识，为进一步研究大型捣固机械作业机理和参数优化奠定了理论基础。

1 数值仿真模型建立

1.1 道砟颗粒模拟及散体道床建模

铁路碎石道砟形态万千，粒径大小各不相同，且各向异性显著[21]，对于道砟颗粒形态的精确模拟及表征是实现大型捣固车捣镐与道砟细观相互作用精细化建模的关键。为真实表征道砟颗粒的形态学特征，本文利用三维激光扫描仪获取了真实道砟三维轮廓.stl 文件[22-24]，并将其导入到EDEM 软件中作为道砟颗粒簇单元中组合球的填充边界，如图1 所示。综合考虑离散元模型的生成速度及计算效率，将导入EDEM 中的道砟颗粒样本分为两类，采用缩减部分道砟颗粒样本组合球数目及占比的方法，减少了道床模型总的球单元数目，缩短了接触判断的时间，提高了模拟计算效率。本文采用的道砟颗粒模板，如图2 所示。

图1 道砟颗粒轮廓扫描过程Fig.1 Scanning process of ballast particle profile

图2 道砟颗粒模板Fig.2 Ballast particle templates

由图2 可知，主要道砟颗粒模板选择了5 种不同的道砟颗粒形态，组合球数目介于10～14，颗粒占比分别为20%、15%、15%、20%和15%，而另一种道砟颗粒模板中组合球数目介于35～50，颗粒占比控制在15%，并且每种道砟颗粒样本均按照图3 的特级道砟颗粒级配来生成不同形态的道砟颗粒。本文生成的道砟颗粒未考虑破碎特征，也未限定颗粒生成的角度或方向，采用颗粒在自重作用下随机堆积的方式构建了散体道床离散元模型，如图4 所示。图4 中道床厚度为350 mm，砟肩堆高为150 mm，砟肩宽度为500 mm，道床顶面宽度为3600 mm；模型中III 型混凝土轨枕采用几何体单元进行模拟，长度为2600 mm，轨下截面宽度为320 mm，间距为600 mm。值得注意的是，生成捣固作业前道床模型时，采用分层压实的方式，使道床密度达到1780 kg/m3，符合《高速铁路设计规范》[25]的要求。一般情况下，由于道床密实度受捣镐振动夹持作用影响较大，捣固作业后的道床密实度会降低。

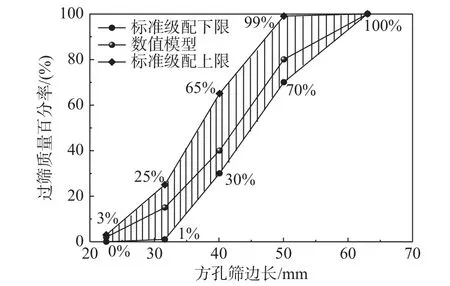
图3 特级道砟颗粒级配Fig.3 Ballast particle gradation

图4 散体道床离散元模型Fig.4 Discrete element model of ballast bed

1.2 三枕捣固装置-轨排-有砟道床耦合模型

DWL-48 连续式捣固稳定车(简称DWL-48 捣稳车)是由捣固车和稳定车两部分构成，是一种结构先进的自行式、多功能线路维修机械。由于其捣固稳定作业过程复杂，结构功能多样，本文仅研究捣固车作业对道床力学状态的影响，如图5所示。图5 展示了DWL-48 捣稳车的捣固车的部分机构及三枕捣固装置(09-3X)。

图5 DWL-48 捣稳车捣固装置Fig.5 DWL-48 tamping and stabilizing machine

为精确模拟三枕捣固作业装置，先根据表1的捣镐镐掌基本几何参数，在solidworks 三维建模软件中绘制了捣固镐的全镐和半镐几何模型，如图6(a)所示。然后，在北京大型养路机械运用检修段实测了三枕捣固装置外镐臂、内镐臂和第三镐臂的几何尺寸，绘制了其几何模型，并与图6(a)的全镐和半镐模型进行装配，生成了三枕捣固装置几何模型，如图6(b)所示。根据《高速铁路设计规范》[25]的相关尺寸要求，在三维建模软件中绘制了钢轨(60 kg/m)和III 型混凝土轨枕的几何模型，如图6 所示。最后，将三枕捣固装置模型(图6(b))和轨排模型(图6(c))的.step 文件导入多体动力学软件RecurDyn 中，生成了三枕捣固装置-轨排-有砟道床精细化耦合仿真模型，如图6(d)所示。需要注意的是仿真模型中钢轨和轨枕之间并未考虑扣件系统，采用固定约束进行了连接，这是由于在捣固作业过程中主要关注轨下捣固区域的力学状态变化，扣件系统对捣固作业效果影响较小。

表1 三枕捣固装置捣固镐镐掌基本几何参数Table 1 Geometric parameters of tamp tine for three-sleeper tamping machine

图6 三枕捣固装置-轨排-有砟道床耦合模型生成过程Fig.6 Generation process of three-sleeper tamping machinetrack panel-ballast bed coupling model

三枕捣固装置-轨排-有砟道床精细化耦合仿真模型中道砟-道砟接触、道砟-轨枕接触、道砟-捣镐接触均采用Hertz-Mindlin(No Slip)本构模型，其中法向接触力分量基于Hertzian 接触理论[26]，切向力模型基于Middlin-Deresiewicz 的研究工作[27]，滚动摩擦力通过接触独立定向恒转矩模型实现[28]。在数值模型中，钢轨与道砟颗粒不直接接触，参考文献[29 - 31]将弹性模量取为2.07×105，密度取为7860 kg/m3，泊松比取为0.3；捣镐、轨枕与道砟颗粒直接接触，为保证接触参数的可靠性，参考文献[17]，将捣镐的弹性模量设为2.07×105MPa，密度设为7900 kg/m3，泊松比设为0.29，轨枕的弹性模量设为3.1×104，泊松比设为0.2，密度设为2240 kg/m3。根据文献[17，32 - 34]中的道砟颗粒材料属性及接触参数，通过控制变量法，结合2.2 节捣固作业前后道床横向阻力试验结果，拟定了仿真模型的计算参数，如表2 所示。

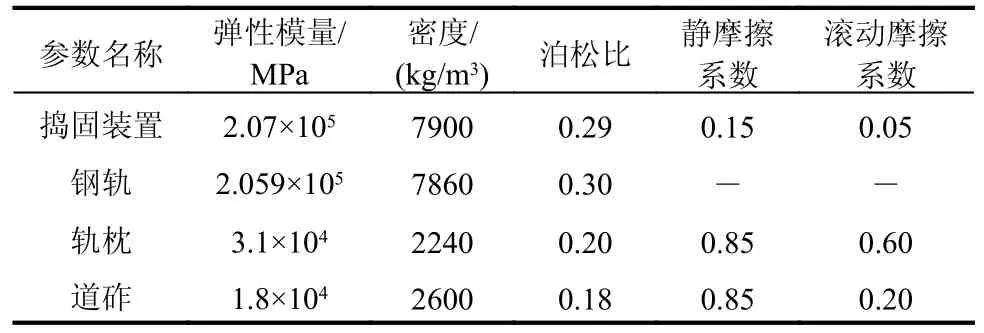
表2 仿真模型接触参数Table 2 Contact parameters of simulation model

考虑到多体动力学与离散元双向耦合计算的稳定性，在数值模型计算时，将计算时步设为Rayleigh 时间步的10%左右，借助GPU 进行加速计算，将一次模型的计算时间控制在8 天以内。

2 捣镐运动施加及模型验证

2.1 三枕捣固装置捣镐运动设置

一个完整的三枕捣固作业过程，包括起道、捣入、夹持、撤镐回转及提升4 个基本作业阶段，如图7 所示。为精确模拟现场实际捣固作业过程中捣镐的运动情况，结合现场养护维修作业中的常用捣固作业参数[10,17]，在捣固作业前将起道量设为30 mm，捣固深度设为386 mm。在图7(a)起道阶段，将作业时间设为0.1s，轨排向上运动的速度设为300 mm/s，各镐尖振幅调整为10 mm，激振频率设为35 Hz。在图7(b)捣入阶段，将作业时间设为0.4 s，并考虑捣镐和道砟间的相互作用，设置捣镐运动为先匀速后匀减速运动，初速度设为1880 mm/s，匀速运动时间设为0.1 s，匀减速阶段加速度设为18800/3 mm/s2。

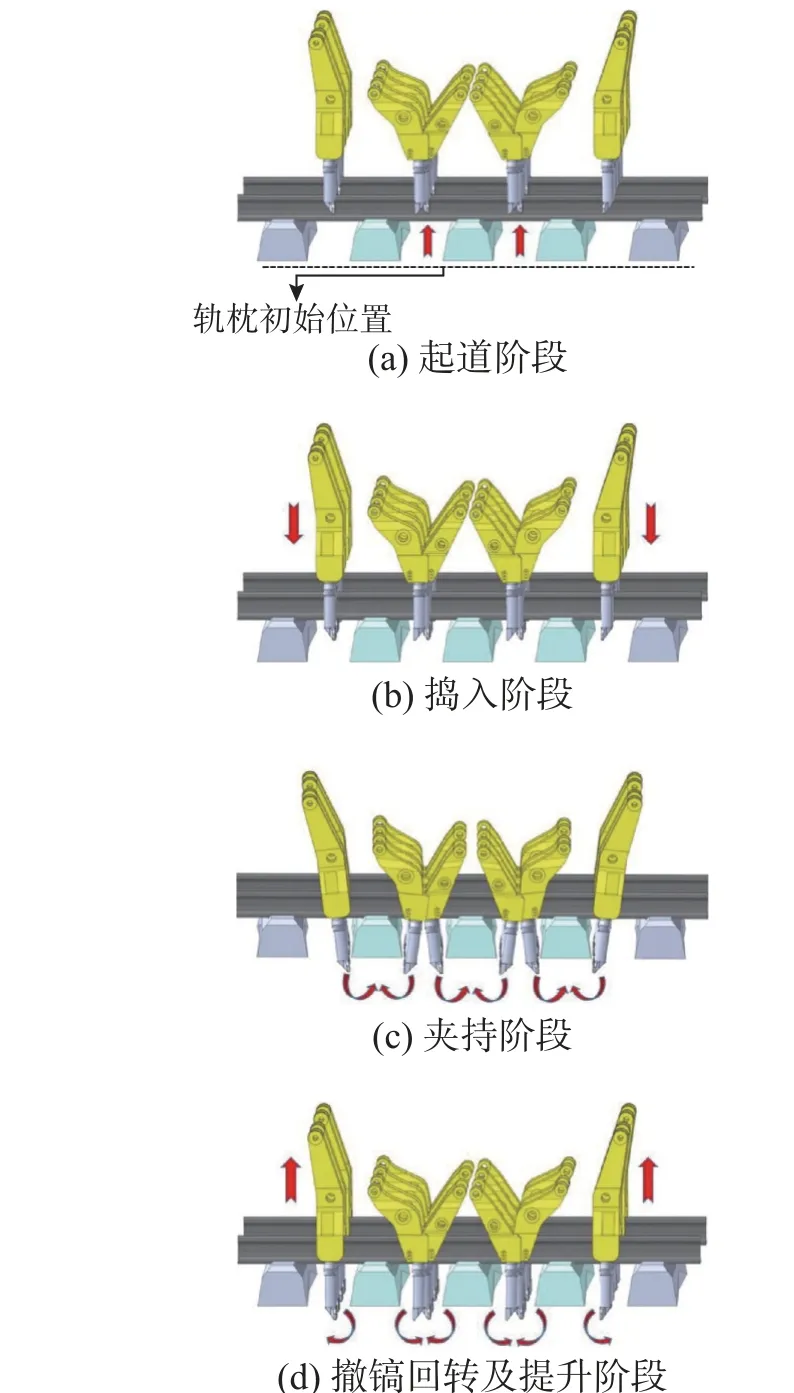
图7 捣固作业过程及捣镐运动Fig.7 Tamping operation process and tamping pick movement

在图7(c)夹持阶段，假设各捣固镐镐尖的线位移相同，将夹持时间设为1 s，根据镐尖至旋转中心的距离、夹持时间与捣镐旋转角度的关系，通过换算得到外镐、内镐和第三镐的角速度分别为7.2 °/s、8.4 °/s 和9.2 °/s。在图7(d)的撤镐回转及提升阶段，先将外镐、内镐和第三镐的角速度设为-14.4 °/s、-16.8 °/s 和-18.4 °/s，持续时间设为0.5 s 来完成捣镐回转作业，然后在各捣镐上施加先匀加速后匀速的运动来完成捣镐提升归位作业，其中匀加速阶段各捣镐加速度为-18800/3 mm/s2，匀速阶段各捣镐速度为-1880 mm/s。

2.2 模型可靠性验证

本文为验证三枕捣固装置-轨排-有砟道床耦合仿真模型的正确性，在北京丰台站附件某高铁线路开展了三枕捣固作业前后道床横向阻力试验[10]，如图8 和图9 所示。现场捣固作业起道量为30 mm，捣镐激振频率35 Hz，捣固时间2.4 s，夹持时间1 s，外镐夹持压力为90 bar，内镐夹持压力为120 bar，第三镐夹持压力为125 bar，行车速度为1 km/h。捣固作业前后道床横向阻力测试结果，如图10 所示。

图8 现场捣固作业车Fig.8 On-site tamping operation vehicle

图9 捣固作业后道床横向阻力试验Fig.9 Lateral resistance test of ballast bed after tamping

图10 道床横向阻力及阻力功试验结果与仿真结果Fig.10 Test and simulation results of lateral resistance and resistance work of ballast bed

由图10 可知，捣固作业可使道床横向阻力降低约51%，且捣固作业前后道床横向阻力及阻力功的试验结果和仿真结果变化规律基本一致。由图10(a)可知，捣固作业前道床横向阻力试验结果为12.07 kN，模拟结果与其相差大约1.33%；捣固作业后道床横向阻力试验结果为5.92 kN，模拟结果为5.75 kN，相差2.87%。由图10(b)可知，捣固作业前道床横向阻力功试验结果与模拟结果相差0.768 J，大约为试验结果的4.27%；捣固作业后道床横向阻力功的试验结果为8.557 J，模拟结果为8.168 J，两者相差4.54%。综上所述，捣固作业前后道床横向阻力及阻力功的试验结果和仿真结果在数值大小、曲线走势等方面均较为吻合，从而验证了三枕捣固装置-轨排-有砟道床耦合仿真模型中接触参数的正确性及模型的可靠性。

3 道砟颗粒细观运动

3.1 道砟颗粒平动

捣固作业过程伴随着捣镐振动、挤压道砟等复杂的力学行为，对于捣固作业过程道砟颗粒平动特征的描述和表征是探明道砟与捣镐间细观相互作用的关键。本文为研究道砟和捣镐间的相互作用，提取了钢轨外侧捣固作业过程中道砟颗粒速度的大小和方向，绘制了不同捣固阶段道砟颗粒速度分布云图，如图11 所示。

由图11 可知，在捣固作业过程中道砟颗粒速度变化规律极为复杂，较大速度道砟颗粒分布区域随着捣固时间的增加，区域面积不断发生变化。由图11(a)～图11(d)可知，在捣入阶段道砟颗粒较大速度分布区域面积随着捣入深度的增加，呈逐渐减小趋势，且较大速度道砟颗粒主要分布在镐掌周围。另外，随着捣入深度的增加，捣镐对道砟颗粒的影响区域先增大后逐渐减小，砟肩区域较大速度道砟颗粒的数目也呈先增大后减小的趋势，但砟肩道砟颗粒在捣入阶段的速度方向均竖直向上，这与捣镐下插速度及振动密切相关。

由图11(e)～图11(h)可知，在夹持阶段(1.38 s除外)镐掌周围的较大速度道砟颗粒数目随着夹持角度的增加而逐渐增多，且枕下镐掌直接作用的道砟颗粒速度方向从弧形向上的运动方式逐渐趋于直线型运动，而镐掌以下区域道砟颗粒的速度呈“喇叭状”逐渐向下延伸和扩展，其影响区域不断扩大；砟肩道砟颗粒速度方向不断变化，始终保持向下的运动趋势，相比于捣入阶段速度明显减小。进一步对比分析可知，在1.38 s 时镐掌周围较大速度道砟颗粒分布面积迅速减小。这是由于捣镐在夹持作业过程中伴随着捣镐左右振动，当夹持方向与振动方向相同时，枕下较大道砟颗粒速度分布区域会明显增大；当夹持方向与振动方向相反时，枕下较大速度道砟颗粒分布面积会迅速减小。综上所述，起道量恒定的情况下，当夹持阶段捣镐的夹持方向与振动方向保持一致时，有助于道砟颗粒快速向枕下区域移动，填充轨枕和道砟之间的空隙，有利于枕下道砟密实。

由图11(i)～图11(k)可知，在撤镐回转阶段，当捣镐回转方向与振动方向相反时，较大速度道砟颗粒的分布面积会增大，尤其在初始撤镐阶段。之后随着撤镐回转角度的增加，镐掌周围的较大速度道砟颗粒数目逐渐减小，且随着捣镐振动方向不断变化，镐掌周围较大速度道砟颗粒的分布形式在中心聚集状态与四周放散状态来回演变，但整个过程中捣镐对道砟颗粒的影响区域却逐渐减小。综上可知，起道量保持不变的情况下，在撤镐回转阶段，当捣镐的回转方向与振动方向相反时，有利于保持夹持阶段枕下道砟的密实性。

由图11(l)～图11(n)可知，在撤镐提升阶段，捣镐主要影响区域为枕间区域。随着捣镐提升高度的增加，镐掌周围较大速度道砟颗粒分布区域逐渐转移到捣镐上沿，且镐掌以下区域道砟颗粒有向下的运动趋势，而镐掌以上区域道砟颗粒有向上的运动趋势，这与捣镐提升方向及道砟填充镐掌所占区域的动态过程密切相关。

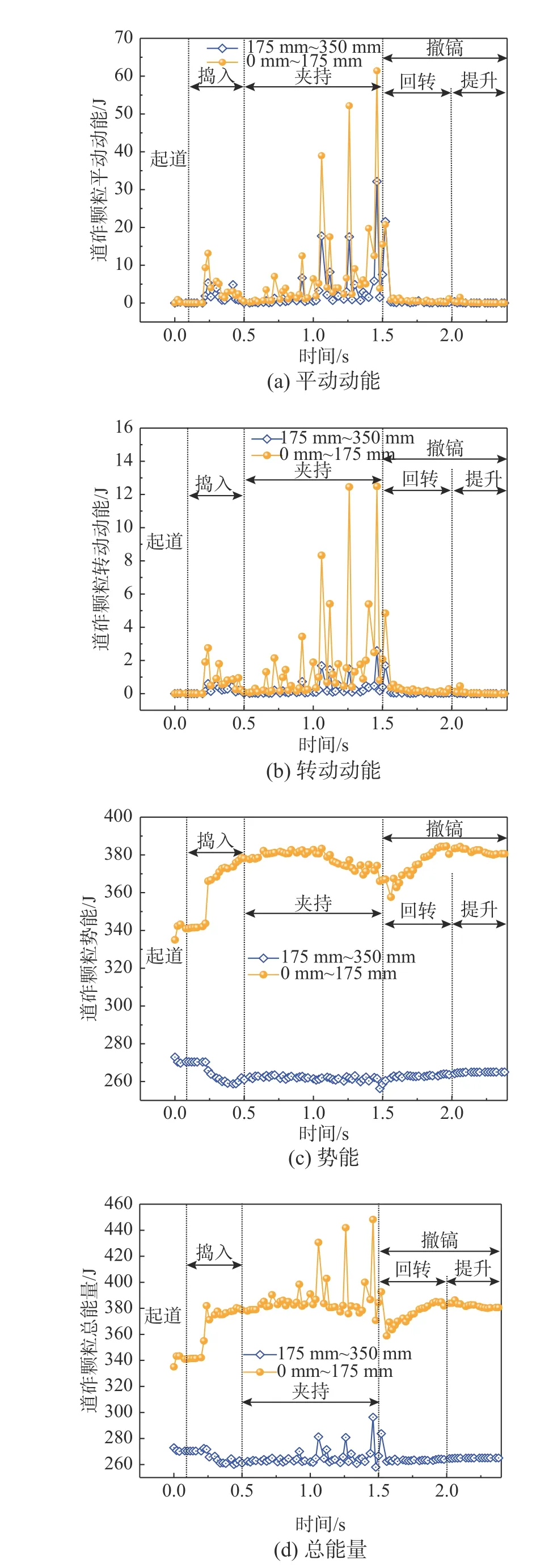
为进一步研究捣镐运动对道砟颗粒平动特性的影响，将捣镐主要作用区域中间轨枕底部道砟颗粒划分为2 部分(0 mm～175 mm 和175 mm～350 mm)进行统计分析，如图12 所示。根据图12 的划分的区域，统计得到了捣固作业过程中各区域道砟颗粒的平均速度，并借助式(1)计算了不同捣固阶段中最大平均速度时刻道砟颗粒速度的概率分布，如图13 所示。

图12 统计区域划分 /mmFig.12 Division of statistical regions

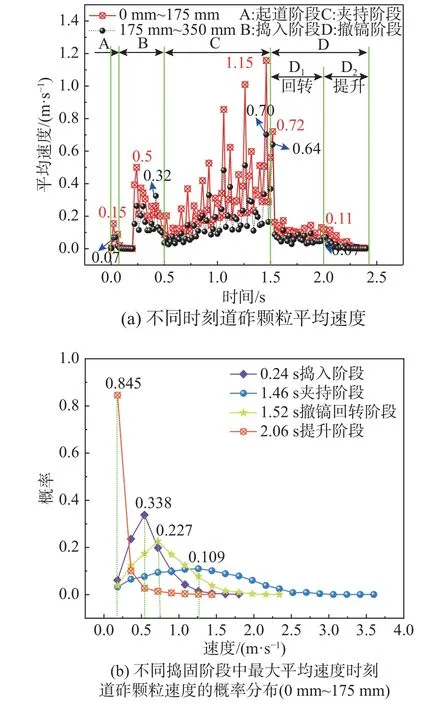
图13 捣固过程中道砟颗粒平均速度变化Fig.13 Average velocity change of ballast particles during tamping

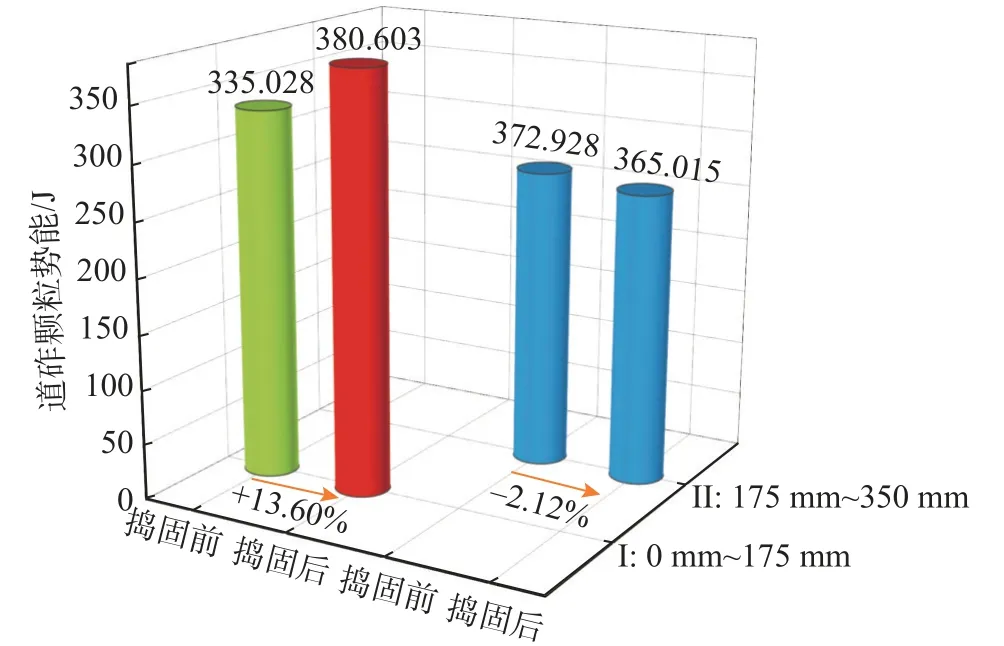
式中：pij为捣固作业第j阶段区域i的最大平均速度时刻道砟颗粒速度的概率分布；Nij为捣固作业第j阶段区域i的道砟颗粒总个数；naij≤xij

由图13(a)可知，随着捣固作业时间的增加，0 mm～175 mm 和175 mm～350 mm 区域的道砟颗粒平均速度均呈先增大后减小，再增大又减小的趋势，且0 mm～175 mm 区域的变化幅度更大。对比各个捣固阶段不同区域的道砟颗粒最大平均速度可知，各区域道砟颗粒最大平均速度均出现在夹持阶段，且随着捣固时间的增加，各捣固阶段的最大平均速度差值呈先增大后减小的趋势，最大差值为0.45 m/s，约为175 mm～350 mm 区域夹持阶段的64.3%，这进一步说明了夹持阶段是枕下道砟密实的关键，也表明了捣镐作业过程中的主要影响区域为枕下0 mm～175 mm，这与图11 中道砟颗粒细观平动规律相一致。

由图13(b)可知，不同时刻(不包括2.06 s)道砟颗粒速度概率分布随着速度的增大，均呈先增大后减小的趋势。捣入阶段道砟颗粒速度占比较高的区域位于0.5 m/s 附近，撤镐回转阶段位于0.75 m/s 附近，提升阶段位于0.2 m/s 附近。这些阶段道砟颗粒速度概率分布曲线极差较大，道砟颗粒速度分布不均匀，道床状态不稳定。而在夹持阶段道砟颗粒速度占比较高区域在1.25 m/s 附近，道砟颗粒速度概率分布曲线极差较小，道砟颗粒速度分布较为均匀，平均道砟颗粒速度较高，填充枕下轨枕与道砟空隙的速度越快，有利于枕下道砟密实，这也说明了枕下道砟密实状态关键取决于夹持阶段与回转阶段的分界点处捣镐与道砟间的相互作用。

3.2 道砟颗粒旋转运动

在捣镐振动、下插、夹持、回转和提升等复杂运动过程中，道砟颗粒平动的同时也伴随着旋转运动，对道砟颗粒旋转特性及转动方式的研究是探明捣固作业过程中道砟颗粒细观运动力学机制的纽带。为研究捣固作业过程道砟颗粒的旋转细观特征，绘制了不同捣固阶段道砟颗粒角速度分布云图，如图14 所示。

图14 捣固作业过程道砟颗粒角速度演变过程Fig.14 Evolution process of angular velocity of ballast particles during tamping

由图14 可知，捣固作业过程中道砟颗粒角速度的变化规律与图11 道砟平动特征变化规律较为相似。由图14(a)～图14(d)可知，在捣入阶段较大角速度道砟颗粒分布区域主要位于镐掌周围，且随着捣入深的增加，较大角速度道砟颗粒分布区域先扩大后逐渐减小，捣镐振动下插动作的影响范围逐渐缩小，砟肩道砟角速度方向也不断发生变化。

由图14(e)～图14(h)可知，在夹持阶段(不包括1.38 s)随着捣镐夹持角度的增加，镐掌下沿与轨枕底部间较大角速度道砟颗粒的分布面积逐渐增大。当捣镐夹持方向与振动方向相反时(1.38 s)，较大角速度道砟颗粒分布面积有减小趋势，这是由于该时刻的捣镐夹持瞬态角位移小于相反方向捣镐的振动角位移。此外，随着夹持角度的增加，砟肩道砟颗粒的角速度逐渐减小，这说明夹持阶段对砟肩道砟颗粒旋转运动影响较小。

由图14(i)～图14(k)可知，随着回转角度的增加，较大角速度的道砟颗粒分布区域逐渐减小，捣镐的影响范围也逐渐减小，且较大角速度的道砟颗粒分布区域由最初的“喇叭状”演变为“椭圆状”。由图14(l)～图14(n)可知，随着捣镐提升高度的增加，较大角速度道砟颗粒的分布区域及捣镐的影响范围逐渐上移，镐掌下沿以上的道砟颗粒角速度有向上的运动趋势。砟肩道砟颗粒在初始提升阶段有向道床内部转动的趋势，而随着捣镐提升高度的增加，道砟颗粒角速度不断发生变化，又有向道床外部转动的趋势，这表明提升阶段后期不利于砟肩道砟密实。

为进一步分析捣固作业对道砟颗粒转动特性的影响，利用3.1 节道砟颗粒速度的统计方法，获得了捣固作业过程中各区域道砟颗粒的平均角速度及不同捣固阶段中最大平均角速度时刻道砟颗粒角速度的概率分布，如图15 所示。

图15 捣固过程中道砟颗粒平均角速度变化Fig.15 Average angular velocity change of ballast particles during tamping

由图15(a)可知，随着捣固作业时间的增加，0 mm～175 mm 和175 mm～350 mm 区域的道砟颗粒平均角速度均呈先增大后减小，再增大又减小的趋势，且0 mm～175 mm 区域的变化幅度更大，这与图13(a)道砟颗粒的平均速度变化规律一致。另外，随着捣固时间的增加，各捣固阶段的最大平均角速度差值呈先增大后减小的趋势，最大差值为24.54 rad/s，约为175 mm～350 mm 区域夹持阶段的114.4%。对比各个捣固阶段不同区域的道砟颗粒最大平均角速度可知，各区域道砟颗粒最大平均角速度均出现在夹持阶段，且捣固过程中各阶段最大平均角速度出现的时间与图13(a)有较好的一致性，这表明当道砟颗粒平均速度达到最大时，0 mm～175 mm 区域道砟颗粒的平均角速度也达到最大，两者具有很好的同步性，这有助于枕侧道砟颗粒填充枕下空隙。

由图15(b)可知，不同时刻(不包括2.06 s)道砟颗粒角速度概率分布随着速度的增大，均呈先增大后减小的趋势。捣入、夹持和撤镐回转阶段道砟颗粒角速度占比较高的区域均位于30 rad/s 附近，但夹持阶段的道砟颗粒角速度概率分布曲线极差较小，道砟颗粒角速度较为均匀，有利于枕侧道砟在捣镐夹持动作迫使道砟颗粒平动的同时发生颗粒转动，减弱了道砟颗粒间的互锁效应，加速了枕侧道砟向枕下空隙运动的速率。此外，道砟颗粒瞬态角速度越大，说明在该时刻道砟向某个方向运动的能量越大，捣镐对道砟作用就越剧烈。因此，道砟颗粒角速度的大小有助于量化捣镐对道砟的细观相互作用。

4 道床内部能量演变规律

捣固作业过程中道床能量的演变规律可以间接反映捣镐和道砟之间的能量传递过程及道床内部的能量传递机理。为研究捣固作业过程捣固区域枕下道床的能量演变规律，绘制了0 mm～175 mm和175 mm～350 mm 两个区域的道砟颗粒平动动能、转动动能、势能及道砟颗粒总能量变化曲线，如图16 所示。图16 中任意时刻的道砟颗粒的平动动能、转动动能及势能，可通过式(2)～式(4)计算得到。

图16 捣固区域轨枕下方道砟颗粒能量演变规律Fig.16 Evolution of ballast particle energy under sleeper in tamping area

式中：Kb道砟颗粒平动动能；mbi为第i个道砟颗粒质量；Vbi为第i个道砟颗粒速度；Mb为道砟颗粒转动动能；Jbi为第i个道砟颗粒转动惯量；ωbi为第i个道砟颗粒角速度；Pe为道砟颗粒势能；hbi为第i个道砟颗粒距离0 势能面的高度；Np为道砟颗粒数目。

由图16 可知，区域0 mm～175 mm 的道砟颗粒平动动能、旋转动能、势能及总能量均大于175 mm～350 mm 区域，这表明捣镐对175 mm～350 mm 道砟颗粒能量传递及演变影响较小。由图16(a)可知，道砟颗粒的平动动能在捣入和夹持阶段的变化最为明显，最大平动动能可达到61.420 J。由图16(b)可知，道砟颗粒旋转动能变化规律基本与平动动能相一致，最大旋转动能为12.490 J 是平动动能的20.33%，这表明捣镐对道砟的作用既有平动也有转动，但道砟颗粒平动所需的能量较大。同时也说明了轨枕下的空隙主要是通过“道砟颗粒以平动为主，转动为辅”的方式进行填充。

由图16(c)可知，随着捣镐作用时间的增加，0 mm～175 mm 的道砟颗粒势能先逐渐增大，后缓慢减小，之后又缓慢增大趋于平稳，最大势能可达384.640 J，是道砟颗粒平动动能的6.26 倍，这说明捣固作业主要影响道砟势能的变化，0 mm～175 mm 区域内道砟颗粒势能提高的越明显，轨枕以下的道床密实度越大，捣固作业后轨枕的下沉量越小。此外，在撤镐回转阶段道砟势能会有减小趋势，这是由于捣镐振动作用使夹持动作后0 mm～175 mm 内的道砟颗粒位置发生了变化，部分道砟颗粒高度会有所降低。

道砟颗粒总能量是衡量任意时刻捣镐给道砟颗粒传递的能量多少的尺度。由图16(d)可知，道砟的总能量在夹持阶段增长的幅度最大，高低起伏也最为明显，这说明了夹持阶段捣镐给道砟传递的能量较多，这与现场捣固作业夹持阶段捣镐做功较多相一致，很好的解释了现场捣固作业的宏观过程对道砟颗粒细观特性的影响。

道砟颗粒势能的变化与捣固质量状态密切相关，可以间接反映枕下区域道床的密实情况。为进一步研究捣固作业对道砟颗粒势能的影响，获取了捣固作业前后0 mm～175 mm(Ⅰ)和175 mm～350 mm(Ⅱ)两个区域的道砟颗粒势能，如图17 所示。

图17 捣固前后枕下区域道砟颗粒势能Fig.17 Potential energy of ballast particles in the area under the sleeper before and after tamping

由图17 可知，捣固作业前Ⅰ区域的道砟颗粒势能为335.028 J，捣固作业后为380.603 J，增长了13.60%；而Ⅱ区域捣固作业前道砟颗粒势能为372.928 J，捣固作业后为365.015 J，减小了2.12%。这表明捣镐主要影响Ⅰ区域，对Ⅱ区域作用较弱，这与图13(a)和图15(a)得出的结论相一致，这也很好的揭示了捣镐和道砟之间能量传递规律。

5 结论

本文结合DWL-48 连续式捣固稳定车捣固装置的实际作业过程，利用离散元与多体动力学耦合仿真理论建立了三枕捣固装置-轨排-散体道床三维空间耦合仿真模型，分析了道砟和捣镐之间的细观运动力学机制，揭示了三枕捣固装置细观作业方式及道砟颗粒的运动形式。具体结论如下：

(1) 利用离散元与多体动力学相关理论，基于缩减部分道砟颗粒样本组合球数目及占比的方式，建立了三枕捣固作业数值仿真模型，通过现场试验验证了模型的可靠性。通过分析现场试验结果发现，三枕捣固作业可使道床横向阻力降低约51%。因此，建议现场捣固作业后应及时进行稳定作业，恢复道床横向抵抗变形能力。

(2) 在捣固作业过程中道砟颗粒速度的变化规律极为复杂，较大速度道砟颗粒分布区域随着捣固时间的增加，区域面积不断发生变化。通过分析道砟颗粒速度变化规律发现，在夹持阶段0 mm～175 mm 区域的道砟颗粒速度概率分布曲线极差较小，道砟颗粒速度分布较为均匀，平均道砟颗粒速度较高，填充枕下轨枕与道砟空隙的速度越快，有利于枕下道砟密实。

(3) 在捣固作业过程中道砟颗粒角速度的变化规律与速度变化规律较为相似。当道砟颗粒平均速度达到最大时，0 mm～175 mm 区域道砟颗粒的平均角速度也达到最大，两者具有很好的同步性，这有助于枕侧道砟颗粒快速填充枕下空隙。此外，道砟颗粒角速度的大小有助于量化捣镐对道砟的细观相互作用。

(4) 捣固作业主要影响枕下捣固区域0 mm～175 mm 范围内道砟颗粒能量变化。捣固作业过程中伴随着道砟颗粒平动动能和旋转动能向道砟颗粒势能的转变过程，且捣镐采用以“道砟平动为主，转动为辅”的方式填充枕下空隙。此外还发现，枕下捣固区域道砟颗粒势能与密实度密切相关，道砟颗粒势能越大，枕下捣固区域密实程度就越好。