面向均匀损伤的RC 框架结构抗震优化设计方法

吴 山，何浩祥，兰炳稷

(北京工业大学工程抗震与结构诊治北京市重点实验室，北京 100124)

基于性能的抗震设计是目前结构抗震减震研究的核心理念和发展趋势。根据工程需求和性能指标，可以将基于性能的抗震设计理论分为基于力、位移、能量和损伤的抗震设计方法[1-2]，其中基于损伤的抗震设计方法更加全面、直观和精确。现有研究表明：根据传统抗震方法设计的结构在实际地震作用下的损伤分布通常是不均匀的[3]，当结构中某些楼层的构件发生较严重损伤时，其他楼层的构件可能处于弹性或轻微损伤状态，材料和构件性能难以得到充分利用。地震下构件和楼层的局部损伤将逐渐累积加剧，损伤分布离散程度过大时某些楼层将出现局部抗力不足或变形过大的情况，导致最终未形成整体化抗震机制而出现薄弱层失效机制[4]，结构抗震能力和安全性急剧下降，最终造成结构功能失效或倒塌。若利用基于损伤的抗震设计方法对结构进行优化设计，使各楼层在地震下具有相似的抗震能力和损伤程度，即可改善或消除薄弱层问题，各楼层的损伤相对均匀[5-6]，显著提高材料利用率和整体抗震能力[7]。

均匀损伤是近年来兴起的设计理念，国内外学者对此进行了有益的探索和尝试。何浩祥等[8-10]提出连续体结构均匀位移和均匀应力优化设计方法，通过力学推导给出结构最优截面尺寸分布和最优刚度分布解析解，并借助智能算法对层间模型楼层刚度进行均匀位移优化，揭示了楼层刚度分布规律，然而连续体结构和层间模型均属于工程简化模型，其抗侧刚度分布优化规律难以直接指导框架、剪力墙等复杂结构设计。XU 等[11-12]针对结构安全性和适用性，分别对弹性结构和弹塑性结构进行均匀位移和均匀加速度优化设计，借助智能算法，得到结构的最优刚度分布，但该研究同样采用层间模型而非复杂有限元模型，其优化方法的普适性和准确性有待提高。白久林等[5-6]采用优化准则法对钢框架进行均匀损伤优化设计，将梁柱截面尺寸作为优化变量，得到了最优截面尺寸分布，并结合易损性分析验证了方法的有效性。之后又对RC 框架结构进行均匀损伤优化，用层间位移角和梁柱端部转角作为损伤指标，对梁柱配筋率进行迭代优化，得到了最优梁柱配筋分布。CHAN 和ZOU[13]采用优化准则法对RC 框架进行了两阶段优化设计，在弹性阶段和弹塑性阶段分别对构件截面尺寸和配筋进行了优化。然而，该方法适用于基于变形的损伤模型(如改进的Park-Ang 模型[14]等)，对于基于能量的损伤模型并不适用[15]，因此有必要利用智能算法等优化工具提出具有普适性的优化方法。HAJIRASOULIHA 等[16]基于Park-Ang 损伤模型，对根据IBC-2009 设计的多个不同层数的RC 框架进行均匀损伤优化设计，根据是否成本恒定分情况讨论，给出了最优梁柱配筋率分布，但并未对优化结果的适用性进行验证。纵观目前均匀损伤优化设计研究，现有关于RC 框架结构均匀损伤优化设计方法研究深度不足且精度较低，缺少具有普适性且精度更高的设计方法。

损伤指数或模型是基于损伤的抗震设计方法的重要参数和依据。在损伤模型研究方面，GHOBARAH等[17]建议采用损伤前后结构静刚度比值量化损伤，但其不能充分反映损伤累积和滞回耗能特性。HE等[18]基于结构整体损伤、层间位移角幅值和滞回耗能循环次数建立了结构多重模糊损伤模型，但其表征滞回耗能特性的能力也比较薄弱。在诸多损伤指数中，Park-Ang 模型[19]得到了广泛应用，其采用构件最大变形和累积滞回耗能双参数量化损伤，然而该指数属于半经验模型，缺乏严密理论基础，多用于构件静力分析，在结构时程分析中效果欠佳，且其阈值收敛不严格，为此国内外学者进行了诸多改进，但仍不能彻底解决问题。相比之下，基于弹塑性耗能差率的损伤模型[15]物理意义明确，适合弹塑性动力分析，且损伤指数严格收敛于0～1，一定程度上弥补了Park-Ang 模型的不足，可采用该模型进行均匀损伤优化设计。

有鉴于此，本文基于OpenSEES 有限元平台和智能算法，提出了面向均匀损伤的RC 框架结构优化设计方法。该方法采用基于弹塑性耗能差率的损伤模型[15]，以各楼层损伤指数相等或相近为优化目标，各层框架柱配筋率为优化变量，配筋率指纵筋配筋率，不包含箍筋。以典型的5 层和10 层结构为例，确定了的框架柱最优配筋方案。最终利用弹塑性动力时程分析和IDA 方法对优化结果的有效性和普适性进行了验证。

1 基于智能算法的均匀损伤优化方法

下文对相关优化方法的数学描述、损伤模型、智能算法及优化流程进行阐述。该优化设计的主要假设包括：1)构件配有足够的箍筋确保其不发生剪切破坏；2)梁柱节点域为刚性，节点域不发生破坏，但构件可出现塑性铰；3)优化前后结构材料用量恒定，即具有同等经济性；4)时程分析中对结构输入三向地震动，选择水平两向损伤终值中较大者作为楼层损伤指数。

1.1 优化问题的数学描述

在地震作用下，对于多高层建筑结构，在各层损伤指数不超过限值的情况下，希望其损伤指数沿结构高度方向的分布尽量均匀。通过对每层RC 框架柱配筋率优化设计，达到上述优化目标。该优化问题可以表述为：

式中：ρi为结构第i层框架柱配筋率；Di为结构第i层的损伤指数；[D]为结构损伤指数允许值，应根据实际工程或业主需求确定；n为结构层数。

1.2 基于弹塑性耗能差率的损伤模型

采用基于弹塑性耗能差率的损伤模型量化RC 框架楼层损伤[15]。在小变形下，结构将产生弹性变形能，卸载后结构恢复到初始状态，不发生损伤。在大变形下，结构发生塑性变形，产生的能量主要是塑性变形能，随着位移增大出现更严重的损伤。若提高结构的承载力，结构在大变形下仍可处于理想弹性状态，不产生损伤，结构的损伤状态与其理想弹性变形能和实际弹塑性变形能之间的差率有关，因此采用该值量化结构的损伤程度。理想弹塑性单自由度体系耗能如图1 所示，假设结构在弹塑性状态时刚度可采用割线刚度km表示，其刚度损伤指数Dk可表示为：

图1 理想弹塑性体系耗能示意图Fig.1 Energy dissipation of an ideal elastic-plastic system

式中：ke为弹性刚度；α 为屈服后刚度系数；uy为屈服位移；当结构处于弹塑性状态时，在位移um处的力为Fm，延性µm=um/uy，周期为Tm。

由图1 可见，结构位移为um实际产生的弹塑性应变能EF为面积SOBCD，相应的理想弹性变形能EE为面积SOAD，面积SABC为两者之差，即弹塑性耗能差ED。基于上述概念提出的基于弹塑性耗能差率的损伤指数可由下式计算：

在单调加载的损伤模型基础上加以改进，可以得到动力作用下的损伤模型。地震动作用下的单自由度体系动力方程为：

式中：m为体系质量；c为体系粘滞阻尼系数；F(x,t)为体系恢复力，线弹性体系的恢复力为kx(t)，k为体系的刚度，x(t)为体系相对于地面的位移响应时程；x¨g(t)为地面运动加速度。

将式(4)各项对相对位移x从x(0)到x(t0)取积分，可得：

式中：EK为体系动能；ED为体系阻尼耗能；EF为体系变形能，包括弹性应变能和滞回耗能；EI为地震动输入能量。

设j为RC 框架的第j个楼层，且楼层在外力Fj(t)作用下已经进入弹塑性阶段，利用试验或有限元方法得到楼层层间剪力FF,j(t)和层间位移uF,j(t)，则楼层弹塑性变形能可表示为EF,j(t)=FF,j(t)uF,j(t)。楼层层间位移幅值为uFmax,j，将Fj(t)乘以降幅系数γ 进行调幅，保证楼层处于弹性状态，此时层间位移时程和幅值分别为uEO,j(t)和uEO,max,j，层间剪力时程为FEO,j(t)。设调幅系数βj=uF,max,j/uEO,max,j，需要将uEO,j(t)乘以β 以使弹性层间位移幅值达到uF,max,j，同时将弹性层间剪力也进行调幅FE,j(t)=βFEO,j(t)。由此可得到地震动作用下RC 框架结构第j层等效理想弹性变形能：

进而可得地震动下已经进入弹塑性状态的结构第j层时变损伤指数为：

式中：FF,j,i和FE,j,i分别为i时刻结构第j层弹塑性状态下和理想弹性状态下的层间剪力；uF,j,i和uE,j,i分别为i时刻结构第j层弹塑性状态下和理想弹性状态下的层间位移。b为结构首次进入弹塑性阶段时对应的时间点，n为从时间点b至现时t的时间步长数。准确确定b值为保证该损伤模型精度的关键。建议按下述方法确定b值：分别计算等效弹塑性刚度时程kF,j(t)=FF,j(t)/uF,j(t)和等效弹性刚度时程kEO,j(t)=FEO,j(t)/uEO,j(t)，然后计算得出等效刚度比时程R,j(t)=kE0,j(t)/kF,j(t)。当R,j(t)首次出现明显大于1 的时间点即可取为b。

该损伤模型计算得到的损伤指数严格收敛于0～1。文献[15]对该损伤模型进行了详细阐述，在此不再赘述。为便于震后损伤评估和加固改造，将损伤指数与震后结构的破坏程度建立对应关系，将震害划分为轻微损伤、中等破坏、严重破坏和倒塌4 个等级，对应的损伤指数如表1 所示。

表1 不同震害等级对应的损伤指标范围Table 1 Damage index range of different damage grades

1.3 智能算法

本优化问题选用差分进化算法(Differential Evolution Algorithm, DE)，该方法优化效率高并且具有较强鲁棒性，基本流程可分为以下几个步骤：

首先，由DE 算法在解空间中均匀随机生成NPD 个D维初始向量，设SG= {Xi,G:i= 1, 2, ···,NPD}为第G代种群，Xi,G为第G代个体，由下式生成：

式中，XH和XL分别为个体的上下限。

之后，DE 算法进入进化阶段，该阶段由三步组成：变异、交叉和选择。在变异阶段，对于每个个体Xi,G，变异向量Vi,G由下式产生：

式中：F为变异因子，取值范围0～1；r1,r2,r3∈{1, 2, ···i-1,i+1, ···NPD}为互不相同的整数，且与当前的目标向量索引i不同，因此要求种群规模NPD 不小于4。

变异算法之后进入交叉阶段，将目标向量Xi,G={x1i,G,x2i,G, ···,xDi,G}和 变 异 向 量Vi,G={v1i,G,v2i,G, ···,vDi,G}通过交叉概率CR 进行二项式交叉生成试验向量Ui,G={u1i,G,u2i,G, ···,uDi,G}，交叉过程可用下式表示：

式中，j∈{1, 2, …,D}，并且CR∈[0, 1]。

最后，进入选择阶段，对试验向量Ui,G和目标向量Xi,G的目标函数进行对比，如果试验向量具有更优的目标函数，则将目标向量替换为试验向量，否则，保持目标向量不变。选择操作按下式进行：

式中，f(x)为优化问题的目标函数。

1.4 优化流程

采用OpenSEES 和Matlab 两种工具实现本优化问题，在OpenSEES 中建立RC 框架数值模型，在Matlab 中采用DE 算法优化结构各层柱配筋率，调用OpenSEES 进行弹塑性时程分析，提取有限元模型响应计算各层损伤指数作为优化依据，实现两种软件之间相互协同调用。优化流程如图2 所示。

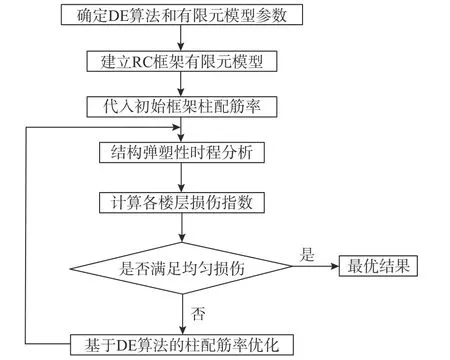
图2 均匀损伤优化设计流程Fig.2 Design process of uniform damage optimization

具体优化步骤如下：1)确定DE 算法收敛阈值、种群个体数等各项参数，以及RC 框架有限元模型的楼层数、梁柱截面尺寸和材料性能等基本属性；2)基于OpenSEES 有限元平台建立RC 框架的有限元模型，代入DE 算法初始变量作为初始梁柱配筋率；3)根据抗震设计反应谱选取合适的天然地震波并进行调幅，对RC 框架进行弹性和弹塑性时程分析；4)提取时程分析得到的弹性和弹塑性各楼层层间位移及剪力，基于Matlab 计算各楼层损伤指数及目标函数值；5)判别是否满足均匀损伤收敛阈值，若满足，优化结束，若不满足，利用DE 算法对各层柱配筋率进行优化，返回步骤3)，进行迭代优化，直至满足收敛条件。

2 算例分析

为验证本文提出的均匀损伤设计方法的有效性和适用性，选取两个典型的5 层和10 层RC 框架结构进行优化设计和分析。

2.1 RC 框架有限元模型

采用有限元平台OpenSEES 分别建立5 层和10 层的RC 框架有限元模型，模型立面和平面如图3 所示，图3 中标注了具体框架梁柱截面尺寸，其中B 代表框架梁，C 代表框架柱。5 层结构梁柱截面尺寸不随结构高度变化，10 层结构由于结构整体高度较高，梁柱截面尺寸随结构高度增大而减小。

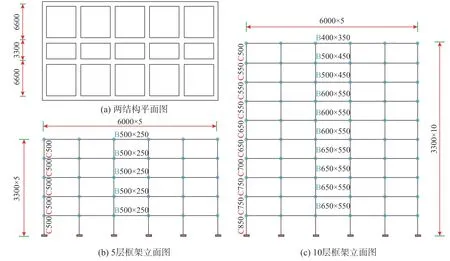
图3 算例结构示意图 /mmFig.3 Diagram of the structures

RC 框架底部与地面固接，在节点处设置集中质量，并施加构件恒荷载和0.5 倍楼面活荷载。钢筋采用Steel 01 模型，屈服强度400 MPa，弹性模量206 GPa，屈服后刚度系数0.01；混凝土采用Concrete 01 模型，抗压强度标准值22.8 MPa，极限强度17 MPa，框架柱的配箍率为2.0%。采用纤维截面(Fiber Section)模拟矩形梁和方柱截面。梁柱截面保护层厚度均为30 mm，对称式配筋。框架梁和框架柱采用基于位移的梁柱单元(Displacementbased beam-column element)模拟。积分类型为“Load Control”；收敛准则采用能量收敛准则，容差1×10-6，最大迭代步数200；迭代算法采用牛顿算法；自由度数目控制设置为“Plain”；矩阵带宽处理采用一般处理方法；约束边界处理设置为致小数或大数法，积分方法选择“Newmark”，γ 取0.5，β 取0.25，分析类型为“Transient”，即恒定时间步长时程分析。结构固有阻尼比取0.05，对结构输入三向地震波，输入至结构一阶振型方向、二阶振型方向和竖向的地震波PGA 比值为1∶0.85∶0.65。

2.2 地震波选取

根据目标反应谱选则5 条吻合程度较好的天然地震波，针对5 条天然波分别进行均匀损伤优化设计。目标反应谱、5 条天然波的反应谱和平均谱如图4 所示。结构按8 度抗震设防，设计基本地震加速度0.2g，Ⅱ类场地，设计地震分组为Ⅱ组，阻尼比取0.05，将输入至结构一阶振型方向的地震的PGA 调幅至0.4g，即大震工况。

图4 目标反应谱和选取地震波的反应谱Fig.4 Target response spectrum and response spectra of selected earthquake waves

2.3 优化结果分析

对5 层和10 层RC 框架有限元模型分别输入5 条天然地震波，利用DE 算法对每层柱配筋率进行优化。随着迭代的深入，式(1)表示的目标函数值逐渐减小，5 层RC 框架结构目标函数收敛阈值为0.08，10 层结构目标函数收敛阈值为0.18，优化过程中目标函数值小于收敛阈值时停止迭代，5 层RC 框架优化过程如图5 所示。DE 算法中，最大进化代数取120，变异因子F取0.5，种群个体数NPD 取20，个体维数D为5 和10，即5 层和10 层框架柱的配筋率，将框架柱配筋率作为DE 算法的优化变量，取值范围为0.8%～3%。

图5 5 层RC 框架优化过程Fig.5 Optimization process of the 5-storey RC frame

本研究取两水平方向损伤指数中较大者作为损伤代表值，为研究其合理性，对未优化的5 层RC 框架结构输入三向Taft 波，算得结构损伤指数如图6 所示。由结果可见，两方向损伤指数平方和的平方根与一阶振型方向损伤指数在数值和变化规律方面区别不大，若两向损伤指数均较大，该值容易超过阈值1，因此不建议该取值方法。两方向损伤指数乘积的平方根取值较小，在一阶振型方向损伤严重时(如8 s～9 s 时段)，该值体现出的结构损伤并不严重，不利于工程安全，因此也不建议该取值方法。由于一阶振型方向损伤指数在多数时段内均明显大于二阶振型方向损伤指数，起主导作用，因此本研究取两向损伤指数中较大值作为代表值。

图6 Taft 波下5 层结构损伤指数时程Fig.6 Damage index time history of 5-storey structure under Taft wave

优化前后的5 层RC 框架结构在El Centro 波作用下各层损伤指数时程如图7 所示，可见优化后结构各层损伤指数离散程度显著降低，并且损伤指数的变化规律与地震波加速度时程关系紧密，在0 s～30 s 时间内，地震动加速度变化活跃，各层损伤指数随之剧烈变化，可见基于弹塑性耗能差率的损伤模型可以较好地表达结构损伤时程及发展规律，适用于评估结构在动力荷载作用下的损伤程度及演变过程，且损伤指数严格收敛于0～1，验证了该损伤模型的优越性。需要指出的是，由于地震动后期随着加速度逐渐平缓及结构自身刚度的恢复，损伤指数会出现一定程度的下降，最终趋于稳定，本研究取损伤终值作为结构损伤指数。优化前结构第i层框架柱配筋率ρei按下式计算：

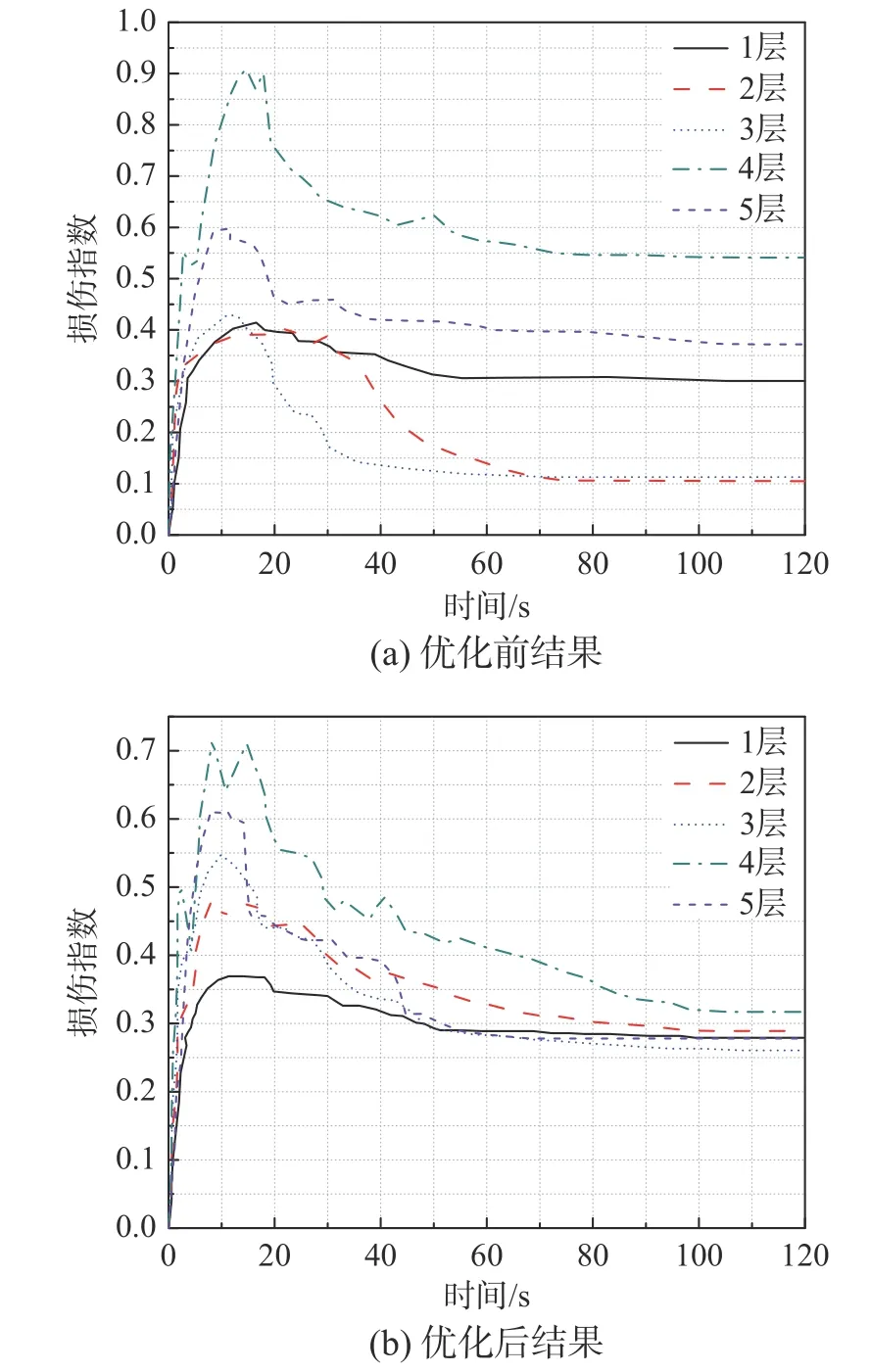
图7 5 层RC 框架在El Centro 波作用下损伤时程Fig.7 Damage time history of 5-storey RC frame under El Centro wave action

式中：ρoi为优化后的第i层框架柱配筋率。如此设置柱配筋率保证了优化前后结构钢筋用量不变，即优化前后结构具有同等经济性，在此约束下可更直观地比较RC 框架各层损伤指数分布的均匀程度。

5 层和10 层结构优化后柱配筋率如图8 和表2所示。由此可见不同地震波下最优配筋率分布未呈现明显的统计规律，由此可以推断该结果和地震波密切相关，不同地震波下的最优配筋率是不同的。

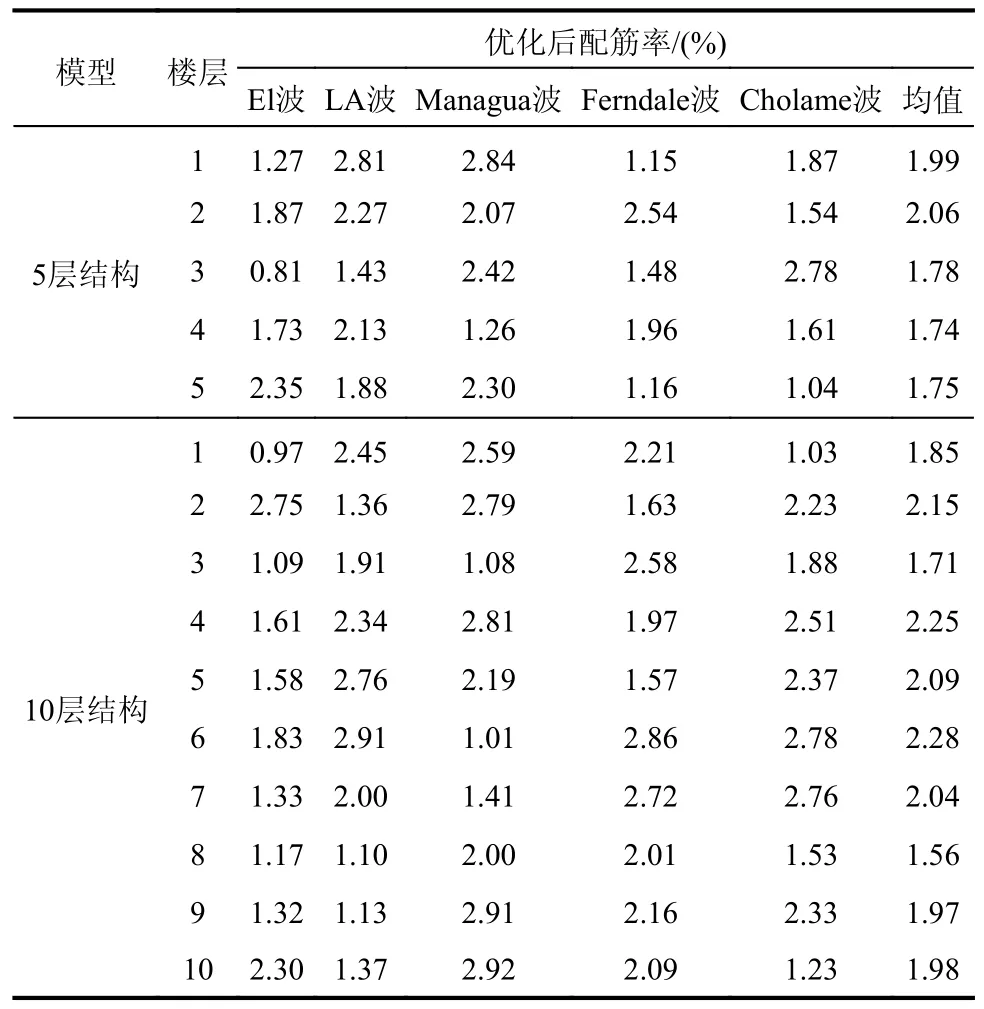
表2 优化后配筋率Table 2 Reinforcement ratios after optimization

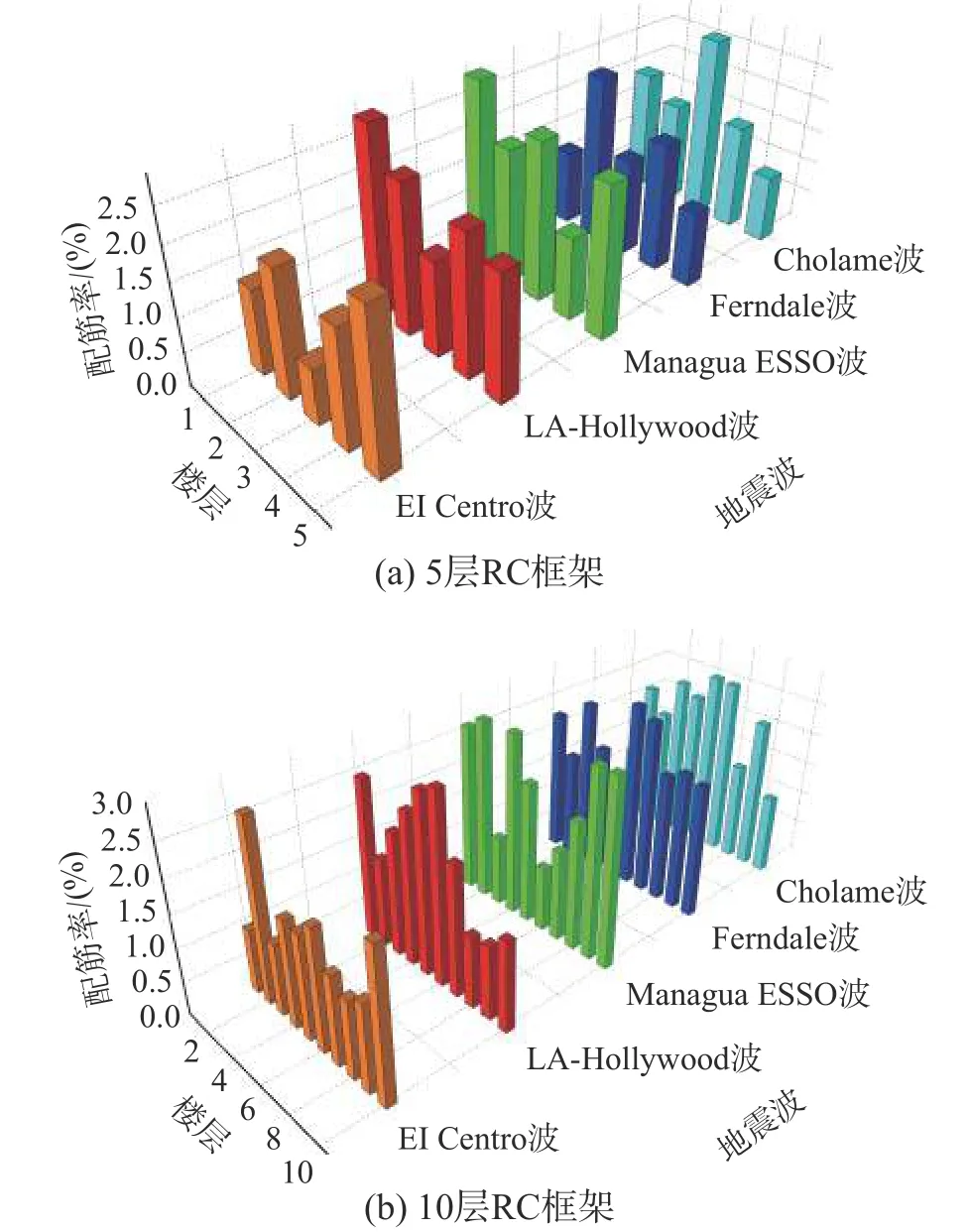
图8 优化后配筋率分布Fig.8 Distributions of optimized reinforcement ratios

优化后的结构损伤指数分布如表3、图9 和图10 所示，可见优化后的结构各层损伤指数明显更加均匀，且满足目标函数收敛要求，实现了优化目标。为进一步研究均匀损伤优化后结构的安全性，提取不同地震波下优化前后RC 框架结构的层间位移角幅值，结果如图11 和图12 所示。

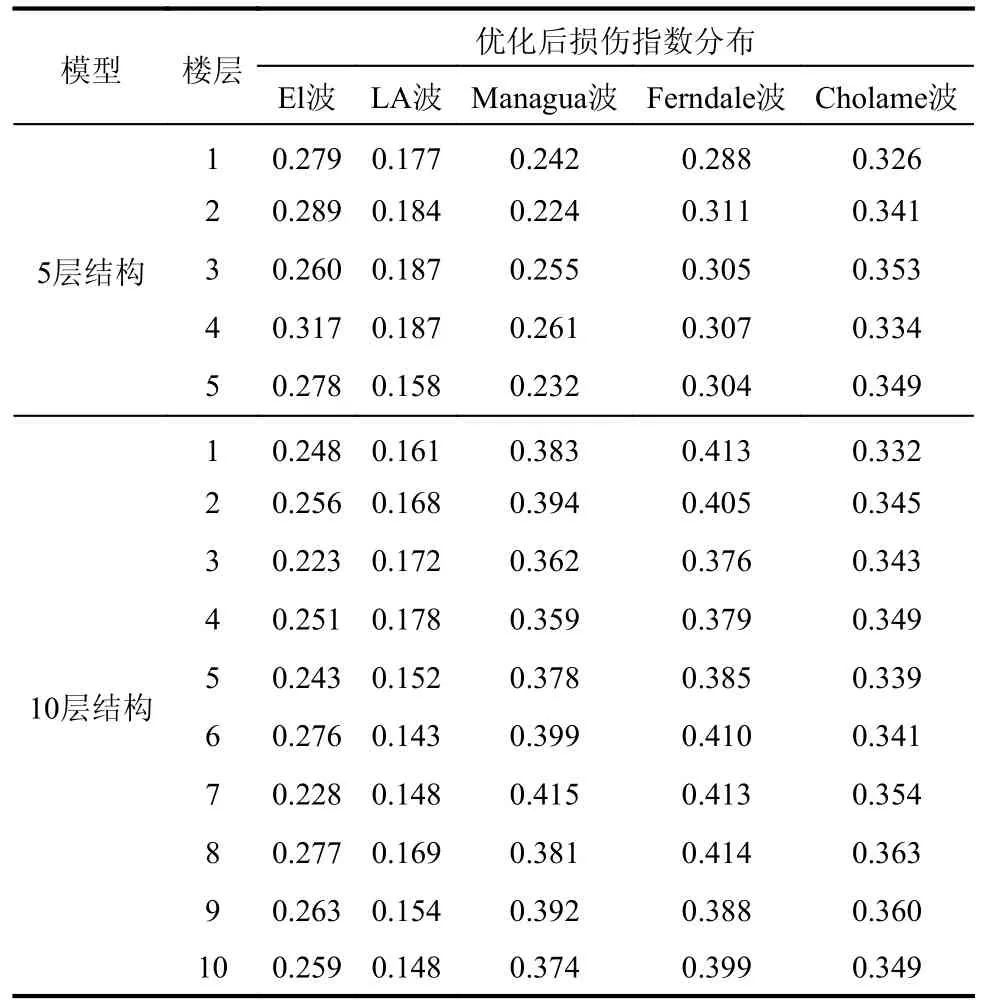
表3 优化后损伤指数分布Table 3 Damage index distributions after optimization

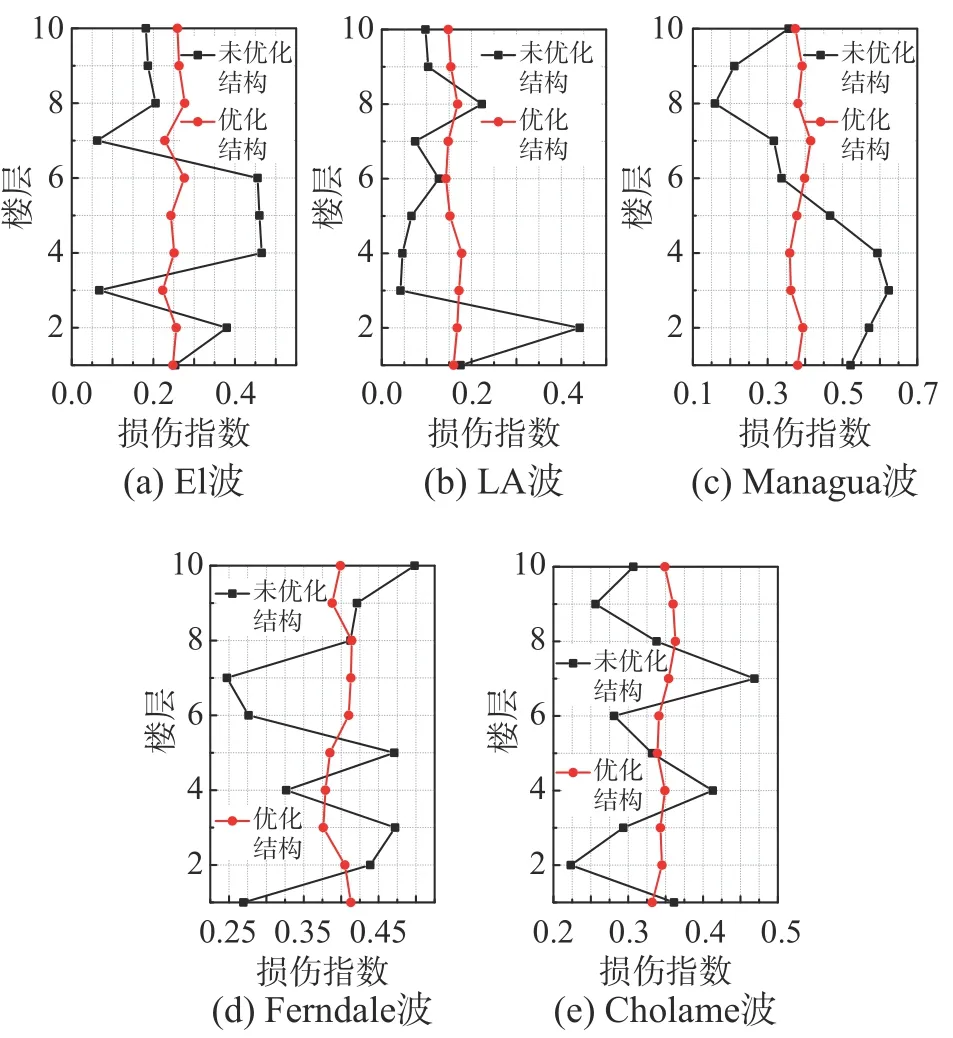
图10 不同地震波下10 层RC 框架优化效果Fig.10 Optimization effect of the 10-storey RC frame under different earthquake waves

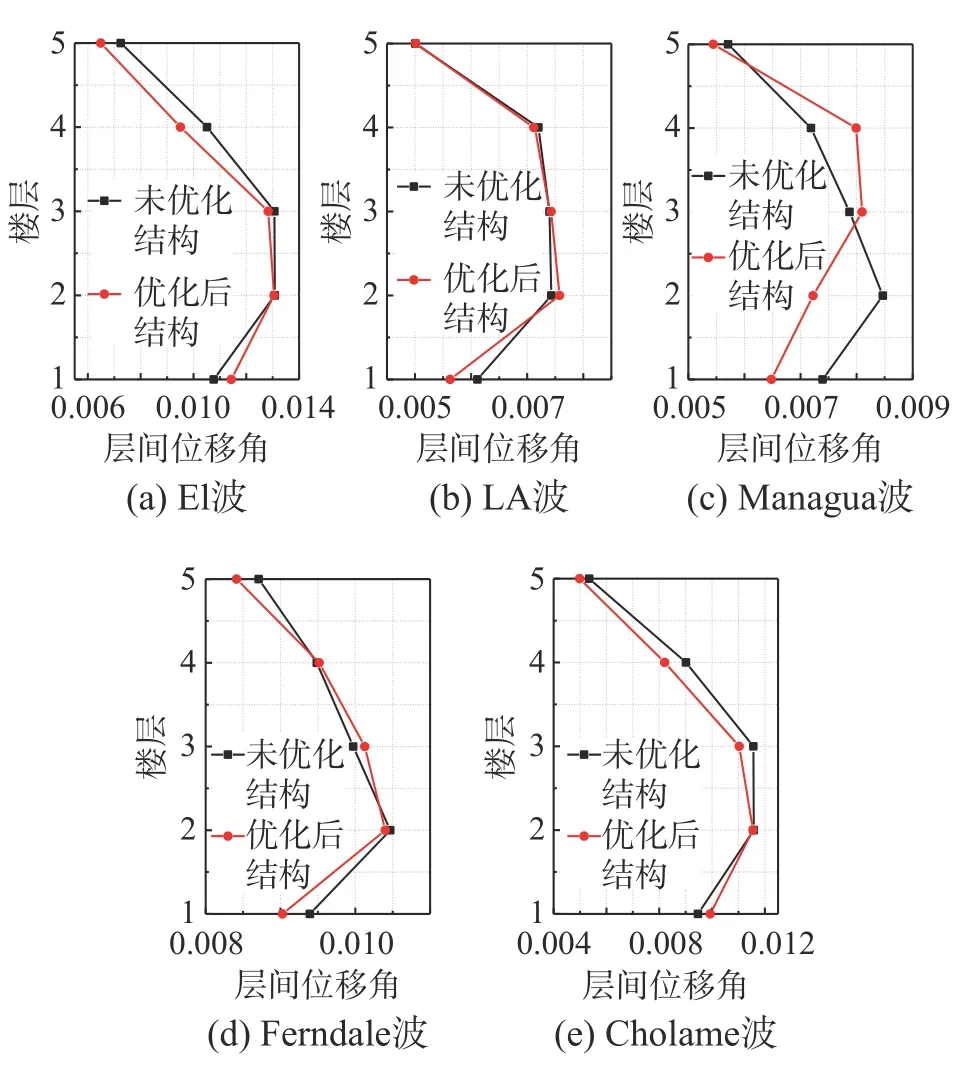
图11 不同地震波下5 层RC 框架层间位移角Fig.11 Story drift ratios of the 5-storey RC frame under different earthquake waves

总体而言，优化后的层间位移角幅值均匀程度和优化前相比区别不大，从传统抗震设计角度来看均匀损伤优化不会显著降低结构体系的安全性。从结构位移角度看，该方法优化效果有限，原因在于本研究优化目标在于令损伤分布均匀，而非令位移均匀，同时采用的损伤模型本质上属于基于能量的损伤模型，与结构耗能相关，是结构动力响应的综合体现，因此优化结果的位移分布不如损伤分布均匀。需要指出的是，本文提出的优化方法具有普适性，根据不同的工程需求与设计理念，同样可采用本方法进行结构均匀位移优化。

3 优化效果验证

上文结合有限元算例，对优化方法和流程进行了展示，并对优化结果进行了分析，为了全面验证本优化方法的有效性，下文对优化前后的结构进行弹塑性动力时程分析和IDA 分析，从结构整体损伤指数、楼层损伤指数分布和地震易损性的角度，对两者分别进行对比分析。采用调幅方法，根据我国规范反应谱选取30 条天然波，其加速度反应谱如图13 所示，其中GM 1-30 代表选取的30 条天然地震波。将30 条天然波的PGA 调幅至0.4g，即大震工况，验证结构整体损伤指数和楼层损伤指数分布均匀程度，基于IDA 方法计算地震易损性，优化后结构每层柱配筋率取表2 中的平均值，优化前结构每层柱配筋率相等，配筋率取优化后结构各层配筋率的平均值，即保证优化前后配筋率总和相等。

图13 地震波加速度反应谱Fig.13 Acceleration spectra of earthquake waves

3.1 结构整体损伤指数验证

在选取的30 条地震波下，优化前后结构的整体损伤指数对比如图14 所示。从结果可以看出，结构整体损伤指数在不同地震波下具有一定离散性，在0.25～0.85 波动，原因在于不同地震波频谱特性不同，对结构的影响程度也是不同的。在30 条地震波中，5 层结构和10 层结构分别存在3 条和4 条地震波的结果是优化后结构整体损伤程度大于优化前的，大多数地震波下的结果都是优化后结构整体损伤程度下降。

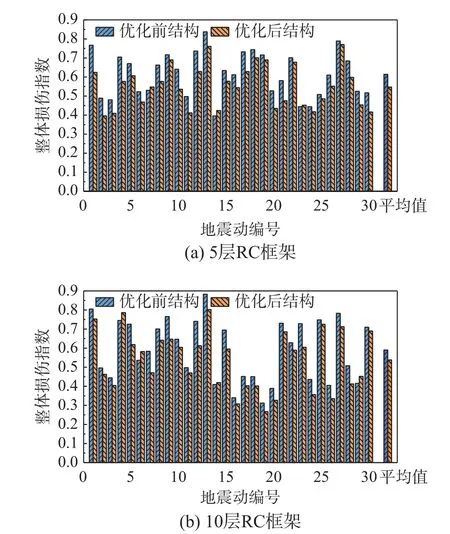
图14 优化前后结构整体损伤指数对比Fig.14 Comparison of the damage index of the unoptimized and optimized structures

优化前5 层结构的平均损伤指数为0.61，优化后变为0.55，较优化前降低了9.8%；优化前10 层结构平均损伤指数是0.59，优化后下降到0.54，降幅为8.4%。从统计意义上表明，优化后结构的整体抗震能力有所提高。

3.2 结构损伤指数分布验证

为进一步验证优化后结构各层损伤指数分布是否更加均匀，计算30 条地震波下结构各层损伤指数的标准差，如图15 所示。从结果来看，5 层和10 层结构的各层损伤指数标准差分别在0～0.2和0～0.3 波动，除个别地震波作用下优化后结构损伤指数标准差有所提高外，绝大多数工况下优化后结构损伤指数标准差均小于优化前结构。优化前5 层结构各层损伤指数标准差为0.13，优化后降低为0.10，降幅为23.1%；优化前10 层结构各层损伤指数标准差为0.12，优化后为0.08，降低了33.3%。由此可见，优化后的结构损伤指数分布明显更加均匀，证明了该优化方法的有效性。

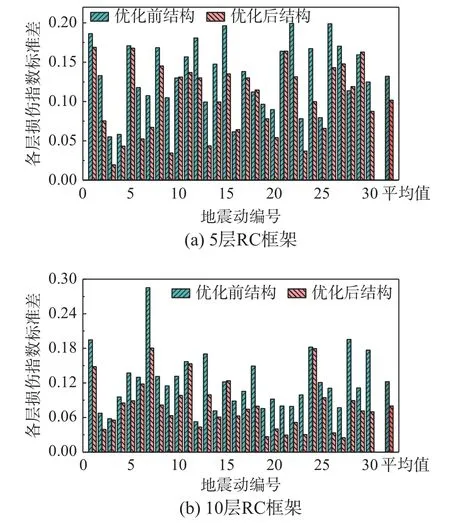
图15 优化前后结构各层损伤指数标准差Fig.15 Standard deviations of the damage index of the unoptimized and optimized structures

3.3 地震易损性验证

基于30 条天然波对结构进行IDA 分析，之后进行地震易损性验证。地震动作用的强度参数(Intensity Measure，IM)为地震动PGA，选取最大层间位移角和基于弹塑性耗能差率的损伤指数作为结构响应参数(Damage Measure，DM)[20-21]，研究表明，IM 和DM 之间存在如下数量关系：

式中：a和b为拟合参数，对式(13)两边取对数可得：

式(14)中A和B可由拟合直接得到。结构失效概率Pf可得：

式中：C为各极限状态损伤指数取值；根据文献[22]的研究结果，当IM 为PGA 时，应取0.5。将PGA 代入式(15)即可得到结构在不同强度地震动作用下的失效概率。

将30 条天然波的PGA 调幅至0.1g～0.7g，对优化前结构和优化后结构进行IDA 分析[23-25]，得到优化前后结构地震易损性曲线如图16 所示。从结果可以看出，结构最大层间位移角和损伤指数易损性曲线呈抛物线形。优化后结构在不同强度地震下的易损性均出现一定程度降低，10 层结构优化效果更加明显，从而进一步证明了优化后结构抗震性能有所提高，验证了本文优化方法的有效性。

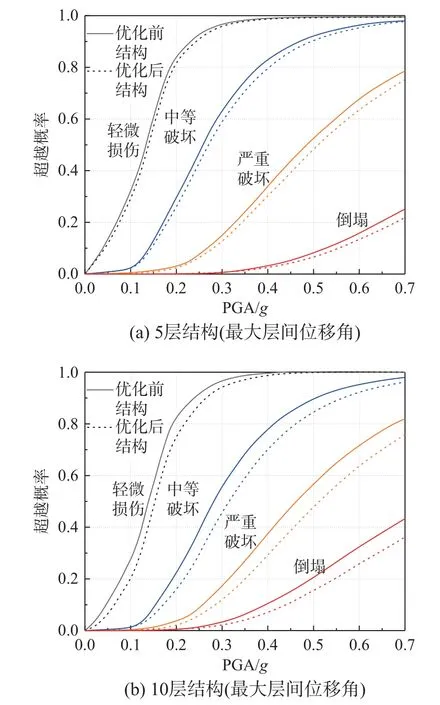
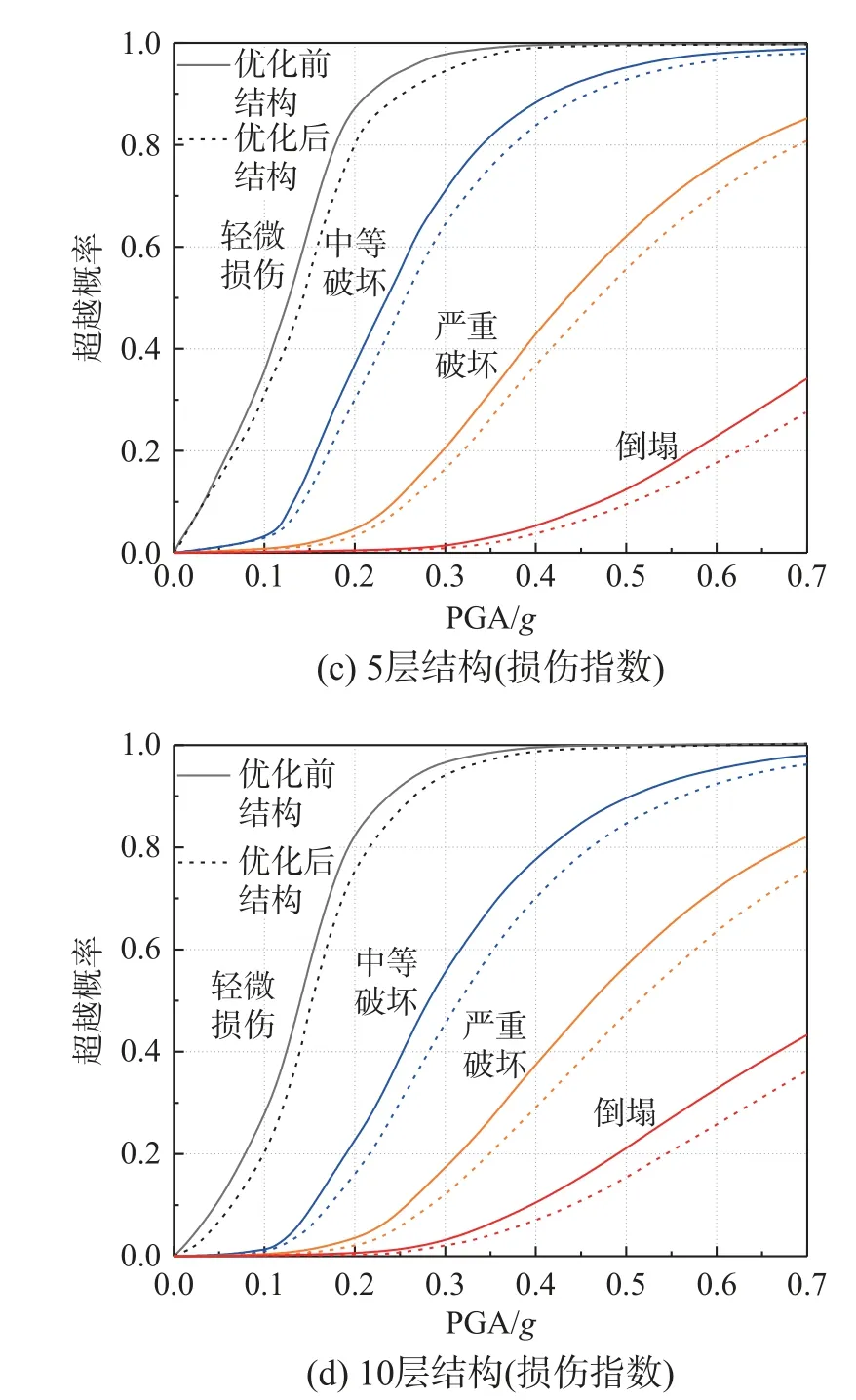
图16 优化前后结构地震易损性曲线Fig.16 Seismic fragility curves of the unoptimized andoptimized structures

需要指出的是，损伤模型存在多样性，采用不同损伤模型得到的优化结果可能是不同的。由于基于弹塑性耗能差率的损伤模型物理意义明确，且适用于动力作用下的结构损伤评估，故推荐采用该损伤模型。本研究不必拘泥于该损伤模型，旨在提出一种具有普适性的优化方法，而且优化对象和优化目标是多元化的，若对装配式结构的构件截面尺寸进行优化，将更有利于实现工程应用。另外，受优化计算量所限，本算例仅采用5 条地震波进行优化，若能得到更多地震波下的优化结果，优化效果会更加明显，而且为降低计算量，提高计算效率，可提高智能算法的收敛阈值，令优化后结构损伤分布适度均匀即可，以此提高该方法的实用性，便于实际工程应用。

4 结论

本文以RC 框架结构各层损伤程度相等或相近为优化目标，以各层框架柱配筋率为优化变量，采用智能算法对结构进行抗震优化设计，实现了真正意义的均匀损伤设计。阐述了DE 算法的基本原理、优化问题数学描述、基于弹塑性耗能差率损伤模型的原理以及优化设计流程，结合RC 框架有限元模型对该优化方法进行了展示和分析，确定了最优框架柱配筋率，并结合弹塑性动力时程分析和IDA 分析对优化结果进行了验证。具体结论如下：

(1)框架柱配筋率是影响RC 框架结构损伤指数分布的重要参数，通过智能算法调整配筋方案可以有效调控结构震后各层损伤程度，实现均匀损伤设计准则，提高结构抗震性能。

(2)不同地震波下结构最优配筋率分布不尽相同，并且不同楼层结构的最优配筋率分布也未呈现明显的统计规律，目前尚难以得到具有通用性的最优柱配筋率计算公式，需要继续进行深入探究。

(3)将不同地震波下优化结果的均值作为框架柱配筋方案可以有效提高结构抗震能力，通过结构整体损伤指数、楼层损伤指数分布和地震易损性的角度验证了该方法的有效性。

(4)通过结构IDA 分析发现，当优化后结构遭遇的地震动PGA 与优化过程中所用地震动PGA 相同时，优化效果比遭遇其他强度地震动时更显著，但优化结果在其他强度地震作用下也是有效的。