1万t重载组合列车测力车钩布置优化

2024-04-10张羽帆和永峰

兰州交通大学学报 2024年1期

张羽帆,薛海,和永峰

(兰州交通大学机电工程学院,兰州 730070)

随着我国客运专线的建成,客货混运将逐步分离,既有线经加固改造开行1万t重载组合列车已成为铁路货运的发展趋势,从而进一步缓解我国大宗货物运输压力[1]。由于受我国既有线设计和建设标准影响,改造后的线路不宜开行大轴重的重载单元或组合列车,为此,需要增加编挂辆数,提高重载列车牵引吨位[2-3]。我国重载列车采用16型和17型非刚性连接车钩,两连挂车辆间存在纵向间隙,且随着车辆服役过程中钩体和钩舌接触区磨损磨耗,配合间隙进一步变大,导致重载列车纵向冲动问题变得尤为突出,危及行车安全[4]。

目前,重载组合列车纵向冲动问题研究,主要采用基于动力学模型的虚拟仿真方法,如常崇义等[5-6]通过重载列车纵向动力学仿真模型,模拟仿真获取不同工况下的纵向载荷信息;Bosso N等[7]通过建立整车货运列车和机车两种仿真模型,研究了列车纵向力对轮轨力的影响,为列车运行安全提供依据。但这些研究存在对列车受载影响因素考虑不全、边界条件与实际情况不符、运营条件复杂多变不能随时反馈等问题。为真实反映重载列车在实际运营工况中的纵向受载情况,通过线路测试可以有效解决上述问题,采取在不同车位处布置多个测力车钩的方案开展载荷信号采集,但由于受测试条件、经济成本、技术手段等因素限制,对于测力车钩的布置主要依靠经验,如王鼎等[8]对2万t重载列车在46次跟踪试验中车钩的纵向受力情况进行了统计分析,为进一步优化列车操纵提供参考。以上研究均未说明测力车钩布置的理论依据,仅依靠经验进行测力车钩布置存在一定的盲目性。通过相关学者[9-10]对于实测的1万t重载组合列车不同工况下不同车位载荷分布特性分析,得出测力车钩所得载荷数据在主控和从控机车附近车位处的载荷特性与其它车位差别较大外,剩余车位处的载荷分布均有相似之处的结论。因此,可通过对不同车位的载荷特性进行统计分析,对载荷信息基本一致的车位进行归类,布置较少的测力车钩表征1万t重载组合列车不同车位的纵向载荷特征,从而实现测力车钩布置位置和数量的优化。

本文在线路实测1万t重载组合列车车钩载荷-时间历程的基础上,统计分析不同车位的车钩载荷特性,并计算不同车位处载荷信号相关指标,采用主成分分析法和分层聚类法,根据不同车位载荷表征参数进行车位分类,优化1万t重载组合列车测力车钩布置。

1 载荷特性

1.1 载荷测试

试验车辆编组为114辆C80型铝合金敞车组成的1万t运煤重载组合列车,从控机车位于第60位车辆前部,将10个测力车钩进行均布轮流布置,设置采样频率为500 Hz,从2到114车位,共测试了16个车位,每个车位测试5次的纵向载荷-时间历程信息。

受机车无线同步控制、司机操作、钩缓装置特性和制动系统配置等因素的影响,在机车牵引启动和制动过程中,不同车位连挂车辆间最大纵向载荷呈现不同,图1为某次测试从控机车后位(60位)和尾端车位(112位)处截取的一段纵向载荷-时间历程,60位和112位的最大拉伸载荷分别为1 168 kN和607 kN,最大压缩载荷分别为1 238 kN和750 kN,分别相差47.7%和39.4%,最大纵向载荷相差较大。

图1 纵向载荷-时间历程

1.2 载荷统计分析

由于纵向载荷-时间历程为随机过程,在车辆不同的运行状态下载荷变化明显,离散性较大,且重载列车关键部件的失效形式主要为动载荷作用下的疲劳破坏。为此,根据疲劳损伤和材料的S-N曲线表达式,推导得到各循环载荷造成的结构损伤占比di为:

(1)

式中:Fi为第i级载荷对应的等效载荷,Di为载荷Fi造成的结构损伤,DZ为载荷造成的总损伤,Ni为i对应的次数。

依据表达式(1)得出:各循环载荷所造成的结构损伤与材料疲劳性能参数m有关,呈指数关系。根据上述分析,将拉伸载荷与压缩载荷进行分离,计算拉伸载荷和压缩载荷均方根值FRMS为:

(2)

式中:N为总循环次数。

计算得到拉伸载荷与压缩载荷的均方根值,结合其平均值进行纵向载荷的统计分析,并与各车位载荷造成的结构总损伤进行相关性分析,得到均值、均方根值与损伤的Pearson相关系数分别为0.81和0.84,表明均方根值较平均值更能反映纵向载荷的实际特性。

采用雨流计数法得到如图2所示的纵向载荷-时间历程的雨流矩阵。由图可知,纵向载荷均值主要分布于-800～900 kN(负值代表压缩载荷,正值代表拉伸载荷),分散性较大,而纵向载荷幅值变化范围主要为0～400 kN。究其原因,均值反映了车辆实时所处运营状态的变化趋势,主要受机车操纵和线路条件影响,而幅值变化受车钩缓冲装置特性的影响,反映车辆运营状态变化趋势的波动性。为此,采用纵向载荷标准差进行载荷变化程度的表征。

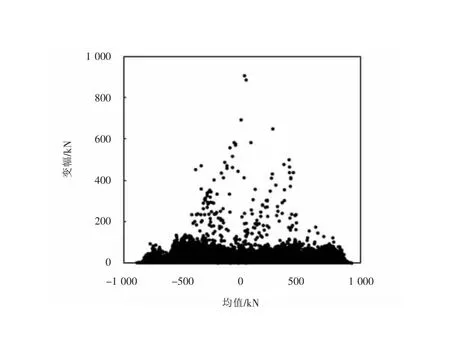
图2 纵向载荷均值-变幅

综上,采用纵向载荷的最大值、均方根值和标准差3个参数进行重载组合列车不同车位处载荷特性的表征,如图3所示,结果表明:主控机车和从控机车后位的拉伸载荷明显大于其他车位的载荷,且以从控机车为分界点,远离机车车位处的最大载荷逐渐减小,而压缩载荷随车位的变化趋势较拉伸载荷平缓;载荷RMS值、标准差与最大载荷的变化规律基本一致。

根据载荷RMS值、标准差与最大载荷的变化规律,采用相关系数进行三个参数的相关性分析,分析结果如表1所示,从中得出:拉伸载荷和压缩载荷RMS值和标准差的相关系数均大于0.90,且最大拉伸载荷与均方根值、标准差的相关系数均在0.85以上,相关性较强;最大拉伸载荷与最大压缩载荷相关性较弱,对应相关系数为0.45。

表1 不同载荷变量的相关系数

相较于上述存在相关性的变量,最大压缩载荷与均方根值、标准差的相关性偏弱,相关系数均低于0.36,究其原因,在列车牵引启动时,各节车辆依序启动,车钩力从最大拉伸载荷到正常运行载荷转变,由于缓冲器刚度变化平缓,导致车辆间载荷变化幅度较小,而列车在制动时,制动波由前往后传递,列车纵向冲击的间隙效应明显,受制动力和前节车辆车钩力影响,后节车辆的速度下降比前节快,故车辆受载由压缩状态向拉伸状态转变,当拉伸状态达到最大时,列车又由拉伸状态向压缩状态转化,此重复过程使得车辆间压缩载荷变化幅度较大,分散性明显。

2 疲劳损伤分析

2.1 载荷谱的分位点外推

(3)

式中:f为载荷-应力转换系数,m、C为材料疲劳性能参数。

由于纵向载荷受机车操纵影响较大,根据实测信号编制的载荷谱不宜按公里数进行倍数外推。为此,采用核密度估计的非参数统计方法进行各车位载荷谱的分位点外推[12-13],获得0.5分位点对应的总谱级损伤,以此表征纵向载荷所造成结构的损伤均值,并采用0.95分位点对应的总谱级损伤表征载荷-次数的分散性。

(4)

(5)

式中:t为同一车位总测试数,Ra(i,j)为某车位第a次测试的(i,j)级载荷对应的雨流矩阵。

根据雨流矩阵的相对偏差分析结果,将具有相似波动的载荷循环组成一个簇,共分成s个簇,分别计算各簇所产生的疲劳损伤值,则同一车位所有测试的t个雨流矩阵产生的疲劳损伤矩阵Di(Rj)为[14]:

(6)

式中:Di(Rj)表示第j个雨流矩阵在第i簇产生的损伤。

基于疲劳损伤矩阵表达式(6),将每个簇的平均疲劳损伤记为μ1,μ2,…,μi,…,μs,与之对应的标准差记为σ1,σ2,…,σi,…,σs。依据式(6)则可得分位点对应的损伤μip为:

μip=μi+kpσi

(7)

式中:kp为正态布置的单边误差限。

为保证各簇损伤按分位点外推的结果与总损伤保持一致,将测试载荷数据中每个雨流矩阵的损伤Di作为离散随机变量,计算所有损伤的均值μD和标准差σD,则得到各簇产生的损伤与总损伤之间的比例系数γi为:

(8)

根据各簇产生的损伤与总损伤之间的比例系数对式(7)的μip进行修正:

(9)

通过概率统计获得外推载荷分级的最大值,确定不同簇的载荷范围,根据式(3),获得不同分位点外推时载荷对应的次数。

图4为从控机车后位0.5和0.95分位点的雨流矩阵外推结果,从中可以得出:较0.5分位点的雨流矩阵,按0.95分位点外推的结果实现了载荷及对应次数的同步外推,弥补了以里程倍数外推的传统方法存在的不足。

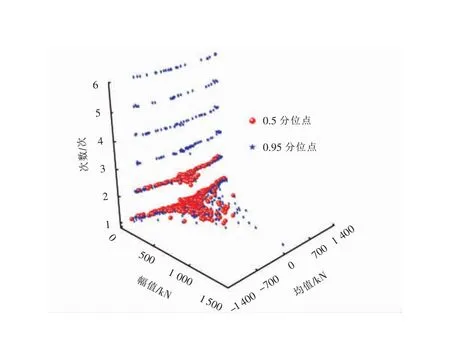
图4 各分位点载荷-频率关系

根据所获得的不同车位在各测试里程对应的雨流矩阵,获得0.5和0.95分位点对应的载荷谱,如图5所示,从中可以得到:超过380 kN载荷的区域,0.5和0.95分位点对应的载荷谱差异性较大,说明该载荷区域载荷次数的分散性较大;在0～380 kN的载荷区域,两者的差异性较小,基本保持一致。

图5 不同分位点的载荷谱

2.2 不同车位的损伤分析

根据所得不同车位的载荷谱,计算得到不同车位0.5和0.95分位点对应的结构损伤,如图6所示,从中可以得到:拉伸载荷所造成的结构损伤主要出现在主控机车和从控机车后位,而远离各机车的车位处所造成的结构损伤呈递减趋势,从控机车前位和整车后端处所造成的损伤较小,约为各机车后位所造成损伤的12%,且各机车后位0.95分位点的损伤比0.5分位点的损伤大;压缩载荷所造成的最大损伤出现在从控机车前后位,该处所造成的损伤约为其他车位处损伤的2倍。

图6 不同分位点的载荷谱

通过不同分位点造成的谱级损伤相关性分析,结果如表2所示。从中可以得到:拉伸载荷的不同分位点损伤相关系数为0.977,压缩载荷的不同分位点损伤相关系数为0.859,具有较好的相关性,但拉伸载荷的相关性优于压缩载荷的相关性,说明拉伸载荷造成的谱级损伤分散性低于压缩载荷谱级损伤分散性。

表2 不同车位的谱级损伤相关性

3 主成分分析

根据1万t运煤重载列车16个车位的载荷特性和谱级疲劳损伤分析结果,选取拉伸载荷和压缩载荷的最大值、载荷均方根值、均值、标准差、0.5和0.95分位点对应的谱级损伤共10个参数为纵向载荷的表征参数。从表1～2的各参数相关性分析可知,各参数间具有较强的相关性,若纵向载荷表征参数过多,且各参数的信息过度重叠,易造成多元共性问题,导致分析结果不准确,同时也使得分析效率降低。为此,利用主成分分析方法,提取有效独立的纵向载荷表征参数,在信息损失量最小的情况下转化为少于10个的综合表征参数,从而降低问题分析计算的复杂性,同时也有利于获取真实全面的有效信息[15]。

由于载荷特性和谱级损伤的物理量纲不一致,且数量级相差较大,需将各表征参数标准化处理。比较多种标准化方法,采用目前使用较多的表达式(10)进行各参数的处理,从而获得各参数平均值为0、标准差为1的标准化值[16]。

(10)

根据表达式(10)得到所有参数的标准化矩阵Y=(yij)n×h,其中n为总车位数,h为指标特征数,通过矩阵Y的协方差矩阵进行主成分的求解。由于矩阵Y的协方差矩阵为原数据矩阵X的相关系数矩阵,则原载荷数据的相关系数矩阵Q为[17]:

(11)

式中:YT为矩阵Y的转置矩阵。

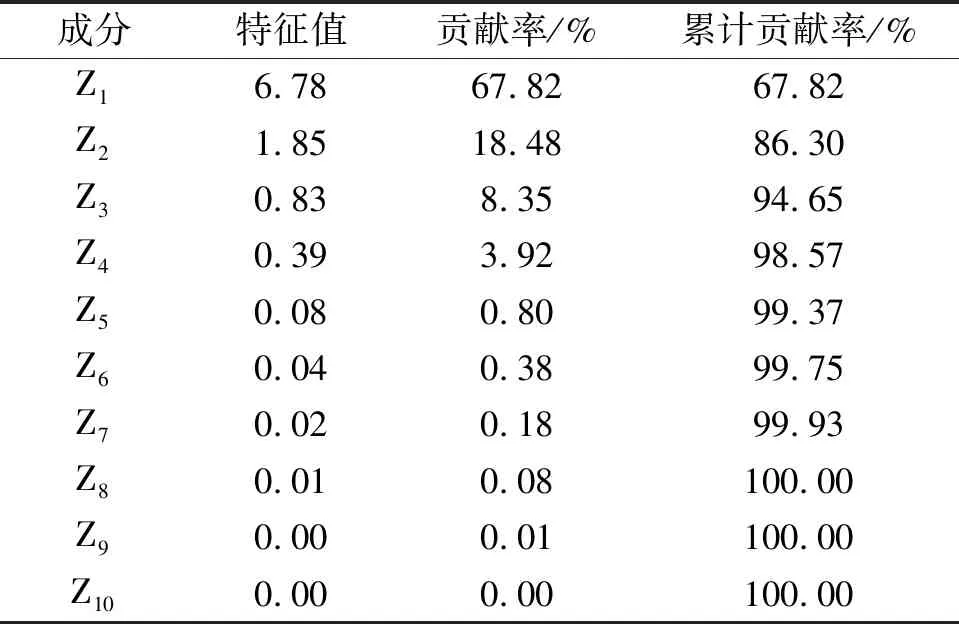
表3 各成分特征值和贡献率

(12)

从表3中可得到:前2个主成分的累计贡献率为86.3%,前4个主成分的累计贡献率达到98.57%,所以采用前4个主成分指标可代替纵向载荷的10个表征参数。

为定量化4个主成分指标与10个表征参数之间的关系,计算前4个主成分表达式的系数,结果如表4所示,从中可得到:第1主成分的系数在0.12～0.37之间,除了最大压缩载荷以及0.5和0.95分位点对应的谱级损伤外,其他表征参数在0.34～0.37之间,说明上述6个因素是表征纵向载荷的主要参数;第2主成分中除了最大压缩载荷以及0.5和0.95分位点压缩载荷对应系数为正值,其他表征参数为负值,说明拉伸载荷对应的载荷特性和谱级损伤的变化趋势基本一致,而压缩载荷的载荷特性和谱级损伤变化的相关性较弱,从图3和图6的结果也证明该结论的正确性;最大压缩载荷对应系数均为正值,表明此类载荷与各类主成分之间均为正相关关系。

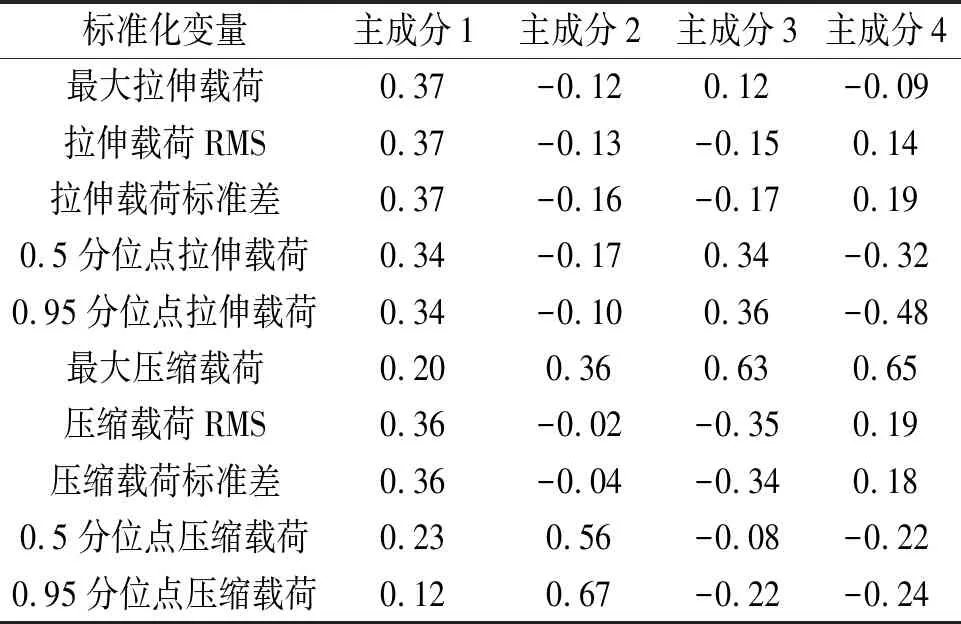
表4 前4个主成分表达式系数

根据表达式(12),可得前4个主成分的得分值,由累计特征值可知,前4个主成分的总方差百分比为98.5%,故可基于该类主成分描述原始数据。绘制第一主成分和第二主成分的得分散点图,结果如图7所示,从中可以得出:根据第一主成分得分,除60位,测力车钩安装位置较近的车位载荷特性相似度较高,表明牵引力传递过程中由于司机操纵、线路条件等原因导致车钩处载荷发生了明显变化;根据第二主成分得分,第54位得分较高,反映出该车位处载荷特性与其他车位的差异性明显,与图6分析结果一致。

图7 主成分关系图

为进一步开展主成分分析,基于表4数据开展综合得分计算,结果如表5所示。

表5 各车位综合得分

由综合得分结果分析,主控机车与从控机车之间车位得分较高,表明载荷造成的结构损伤在主控机车与从控机车间车位较大。统计车位中,位于从控机车前位、后位的载荷损伤均远离各机车的车位处呈递减趋势,与前文分析结果一致。

4 测力车钩布置优化

为进一步验证通过主成分分析对测力车钩布置优化的准确性,在主成分分析得到新的载荷综合指标的基础上,应用分层聚类进行分析,并将优化得到的测力车钩布置位置和数量与主成分分析进行比较。

分层聚类作为聚类分析方法之一,具有操作简单、快速准确、易于实现等优点,在实际应用中较普遍,其基本思路是将距离最近的样本先聚成类,距离远的样本后聚成类,该过程循环,则每个样本最终将聚到适当的类中[18]。

两车位间的载荷特征相似度与之对应的距离成反比,通过计算车位相互之间的距离度量其相似程度。由于欧氏距离具有明确的空间距离概念,且在进行聚类分析前对参数进行标准化处理,故采用欧氏距离表达式(13)进行不同车位间4个主成分距离计算[19]:

(13)

式中:d(xi,xj)为第i、j两个车位间的欧氏距离,xiz为第i个车位的第z个指标,h′为车位综合表征参数总数,n为总车位数。

在确定车位间的距离计算方法时,需确定类与类之间的距离。由于类间距离定义的差异会产生不同的系统聚类方法,对比不同类间距方法,得出类平均法对提取所有车位间的信息较为完善,聚类效果较好,应用范围较广。为此,采用类平均法计算类间距离,其表达式为:

(14)

式中:nα、nβ分别为类Gα和Gβ的车位数。

当式(14)中的Gα,Gβ再合并为一类为Gr时,系统聚类中任意一类Gξ与Gr的距离为:

(15)

合并距离最近的2类,根据表达式(14)和式(15),重新计算类间距离,如此循环,直至所有车位合并为1类。

由于车位总数为16个,故设置最小聚类数为2,最大聚类数为16,得到不同聚类数对应的分层聚类结果,聚类谱系图如图8所示。

图8 聚类谱系图

对比图7主成分分析和图8聚类分析结果,聚类效果基本相同,且分散性较大的60车位和54车位也保持了一致,故根据谱系图和主成分图,以及车钩测试中的实际情况,将所有车位分为4类,各类车位如表6所示。

表6 聚合结果

为了检验分类结果是否合理,分别统计4类车位的载荷特征,包括0.95分位点平均损伤数、0.5分位点平均损伤数、平均均方根值、平均最大值和平均标准差,结果如表7所示,从表中可以得出,4类车位的各类载荷特征均具有明显差异,说明基于主成分数据的系统聚类分析对测力车钩的分类是合理的,测力车钩至少应在上述4类车位中均有布置。考虑到实际车位载荷的布置特性和分层聚类结果,测力车钩可优先布置在60位、54位、96位和114位,即测力车钩最小数量应为4个,且优先布置于从控机车前位和后位各1个,从控机车和尾车中央位置1个及列车尾部1个。