近场双向地震动输入的隧道响应分析

杨楚凡,王 伟,张 磊,汪俊诚

(1. 河海大学 土木与交通学院,南京 210098;2. 湖北省水利水电规划勘测设计院,武汉 430000;3. 天津轨道交通线网管理有限公司,天津 300000)

地震是由板块之间的相互挤压和碰撞引起的边缘和内部的位移和断裂所造成的。它往往造成严重伤亡,并可能导致次生灾害发生,是人类最重要的自然灾害之一。我国的地震灾害十分严重,地震活动区分布较大,大部分地区处于地震频发区,地震重灾区往往在活断层附近,并且在断层区域内受到的影响危害最大[1-3]。近断层地震动对地面结构会造成严重的破坏,这已得到不少学者研究。杨迪雄等[4]研究了钢混框架结构在近断层两类脉冲效应地震动作用下的响应,发现断层地震动对结构的破坏更加严重,危害性更大;陈令坤等[5]和Sehhati等[6]分别研究了受近断层破裂向前方向性效应地震动作用下的高速铁路桥和多层框架结构的动力响应影响研究,表明地震动中的速度脉冲会对结构产生更大的延展性;Wang等[7]对近断层地震动作用下的混凝土重力坝进行了动力响应分析,发现考虑近断层地震动的影响很有必要;宋健等[8]依据汶川地震中滑坡断层特点,利用FLAC分析了边坡在两类速度脉冲效应的近断层地震动和无速度脉冲的近断层地震动作用下的动力响应的影响,得到了有脉冲的地震动对边坡影响更大。在工程结构的地震响应规律和抗震问题上,近断层地震动的特性对其影响很大[9-10],越发得到地震工程界学者们的重点关注。

地面建筑在地震发生时,受到的振动程度较大,因此基于地面建筑的抗震理论的发展较早。而地下结构由于周围土体作用,在地震发生时相对于地上建筑所受到的影响程度较小,因而隧道及地下结构的抗震理论和对其抗震问题的研究相对晚一些。但最近几十年,不论公路隧道、跨山隧道还是地下隧道都得到大量发展,因而也有不少报道关于地下结构的震害,让人们意识到地下结构可能所存在的危险。不少学者通过数值软件建立隧道结构有限元模型,分析了软弱土层地区隧道的相对水平位移及动应力响应受竖向地震动的影响[11];分析了地震动不同输入方向对隧道洞口段的动力响应影响[12]以及近远场地震动对深软土场地的双层竖向重叠隧道的响应影响[13],很少有分析近断层地震动对隧道动力响应的影响。尹超等[14]和朱星宇等[15]建立了包含断层破裂面的隧道三维动力分析模型,分别分析了采用人工合成地震动输入下不同截面形式(马蹄形和箱型曲拱)的隧道动力响应以及断层地震动竖向效应的隧道动力响应影响,考虑了断层破裂面影响的隧道动力响应。梅贤丞等[16]结合场地地震设计谱选取了近远场地震动对多山隧道进行增量动力分析,得到损伤概率规律;陶连金等[17]选取了近断层破裂向前方向性和滑冲效应地震动对典型单层三跨地铁车站进行动力时程分析,得到不同脉冲特性下的地震响应影响。王杰等[18]利用ABAQUS分析了双线盾构隧道在水平及竖向地震共同作用下的结构响应,发现双向地震输入相对于单向地震输入,隧道的地震附加内力及分布发生很大变化,但分析所选地震记录相对较少。

目前地下结构抗震设计规范都是基于单向水平或竖向地震的抗震设计,而在近场地震记录中,水平和竖向地震动的加速度都较大,因此考虑竖向地震动与水平地震动共同作用对隧道响应的影响很有必要。本文选取了20组地震动,水平地震动通过最大方向合成以及脉冲地震动提取处理,通过在模型底部输入做双向地震动对隧道结构的影响分析。

1 数值模型建立

本文根据某地区双向矩形隧道为参考,单跨结构净宽8.65 m,两中柱间净宽为1.5 m,中柱厚度为0.6 m,标准隧道横断面宽为23 m,高度为9 m,两侧墙厚度为1.5 m,顶板厚度为1.5 m,底板厚度为1.25 m。土体深度设置为60 m,分别由4层不同土质土体组成,土层厚度依次为5 m、10 m、15 m、30 m,隧道结构在土层埋深为10 m,土层底部假设为基岩面,土层材料参数如表1所列,土体本构采用基于Davidenkov骨架曲线的土体动力非线性粘弹性本构模型[19-20]。本文数值计算转化为横截面平面应变问题进行计算,隧道周围土体采用四结点平面应变实体单元模拟,隧道部分参数采用线弹性,采用四结点平面应变实体单元模拟,参数如表2所列。

表1 土层参数

表2 隧道参数

由于振动或波动要向无限远处传播,在研究土-结构的动力相互作用的问题上,研究对象是一个半无限空间,而在有限元的分析中对象为有界域。地下隧道结构抗震问题为典型的土-结构的动力相互作用问题,通常在有限元建模时进行一些边界设置,达到可以忽略边界效应的影响。本文所建模型左右对称,如图1所示,地基模型为500 m×60 m,地基宽度远大于地下结构宽度5倍,可以忽略边界效应的影响[21]。通过ABAQUS软件对隧道结构进行建模,土体与隧道接触面两侧网格尺寸为0.5 m,200 m土体范围内网格尺寸都为1 m,再向外网格则逐渐变大,隧道及周围土体主要研究部分的网格划分均满足要求。土与隧道结构面之间采用tie接触,计算模型两侧采用自由边界,底部边界考虑为加速度刚度边界,静力计算时底部为固定,主要进行地应力平衡过程,动力计算时底部根据所输入地震动的方式释放约束。地应力平衡过程,动力计算时底部根据所输入地震动的方式释放约束。

图1 隧道有限元模型图

2 地震动选取

地震发生在空间和时间域上均具有高度的不确定性。本文以正北方向为0度,按顺时针变化,通过以每1度进行旋转,得到最大合成PGA的地震动加速度时程及其方位角,判定其具有明显的脉冲效应,同时为了对比分析有无脉冲型地震动作用下结构的响应,不可忽略地震动时程具备同源性和反应谱相似性的特性[22]。因此采用LSF法[23]对脉冲进行提取,可以得到与原始方向性效应引起的速度脉冲地震动(forward directional pulse ground motion,FD)同源但不含速度脉冲的无脉冲地震动(non-pulse ground motion,NP),经过处理的NP地震动在长周期段是不含有速度脉冲成分。近场地震动RSN178的原始速度及脉冲速度处理时程曲线如图2所示,从图中可以明显看出近场地震动具有方向性效应及大速度脉冲等特性。

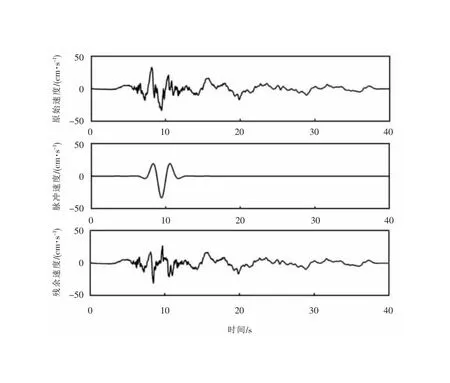
图2 Imperial Valley-06地震动(RSN_178)

本文从断层距小于30 km的方向性效应脉冲地震中选择20组作为计算数据,水平加速度峰值取0.3 g,并且按照规范建议取值竖向加速度av与水平加速度ah峰值比为2/3进行计算,双向地震输入计算的信息如表3所列。

表3 双向地震动计算所选的地震参数

3 计算结果分析

本文将选定的FD地震动与NP地震动共40组地震动作为输入对矩形隧道进行地震响应分析,主要分析双向地震动对隧道的加速度、位移及其应力响应的影响。定义竖向地震动输入的影响率为双向输入地震动响应与单向输入地震动响应的差值和单向输入地震动响应之比,公式如下:

(1)

式中:K为隧道结构响应值,γ为竖向地震动输入影响率。

3.1 双向输入加速度响应分析

单、双向地震动输入下PGV对隧道结构底部和顶部水平加速度的影响如图3所示,从中可以看出,随着PGV的增大,加速度响应也是不断增大的,单双向地震输入计算结果规律一致,并且相差不大。

图3 单双向地震动作用下PGV对隧道峰值加速度影响

FD和NP地震动作用下隧道底部的加速度响应时程的代表工况如图4所示,从图中时程曲线可以看出FD和NP地震动的响应趋势基本一致,但存在脉冲部分的FD地震动的加速度响应要明显大于NP地震动的加速度响应。20组FD和NP地震动作用下隧道底部的加速度响应关系如图5所示,从图中可以明显看出,FD地震动作用下的加速度响应是远大于NP地震动作用下的响应,可见速度脉冲对结构带来的影响不容忽视。通过计算单、双向地震动作用下隧道结构底、顶部加速度响应的峰值水平加速度值(m·s-2)以及脉冲影响系数和竖向地震动输入的影响率,可以发现竖向地震动的输入对结构的水平加速度响应对比于单向地震响应并不都是增大的,由于地震波在土层传播过程中都会发生反射和折射,因此竖向地震动的输入也会对水平加速度有一定的影响,但是影响都是较小的。

图4 FD和NP地震动的隧道底部加速度响应时程

图5 20组FD和NP地震动的隧道底部加速度响应

不论是FD地震动还是NP地震动作用下,竖向地震动输入对隧道结构底部的水平加速度影响率基本分布都在±5%之内,影响较小(顶部规律一致),结果如图6所示。水平向NP地震动下加速度响应的竖向影响率分布比较窄而尖,表明竖向输入对于水平向NP地震动的影响较小;而水平向FD地震动下加速度响应的竖向影响率分布比较宽而矮,表明竖向输入对于水平向FD地震动的影响范围相对较广;底部分布相对比较窄而矮,表明隧道结构底部加速度响应相对来说更会受到竖向地震的影响。

图6 竖向地震动输入对加速度响应影响率

3.2 双向输入位移响应分析

单、双向地震动输入下PGV对隧道结构相对水平位移的影响如图7所示,从中可以看出,随着PGV的增大,位移响应也是不断增大的,单双向地震输入结果一致。

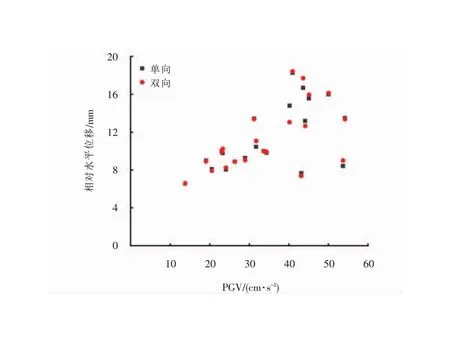
图7 单双向地震动作用下PGV对隧道相对水平位移影响

FD和NP地震动作用下隧道相对水平位移响应时程的代表工况如图8所示,从图中时程曲线可以看出FD和NP地震动相对水平位移响应趋势基本一致,但存在脉冲部分的FD地震动的响应要明显大于NP地震动的响应。20组FD和NP地震动作用下隧道的位移响应关系如图9所示,从图中可以反映隧道结构的位移响应受速度脉冲的影响很大,FD地震动作用下的位移响应远大于NP地震动。通过计算单、双向地震动作用下隧道结构的相对位移值(mm)以及脉冲影响系数和竖向地震动输入的影响率,可以发现竖向地震动的输入对结构的位移响应对比于单向地震响应也不都是增大的。由于单向水平地震动作用时,隧道结构发生变形在水平方向上移动或者旋转,竖向地震动的输入会使得隧道会产生上抛运动,竖向位移产生了很大的变化,加上土体的约束作用,使得对隧道结构水平方向的位移产生很大的影响,变形图如图10所示。

图8 FD和NP地震动的隧道相对水平位移响应时程

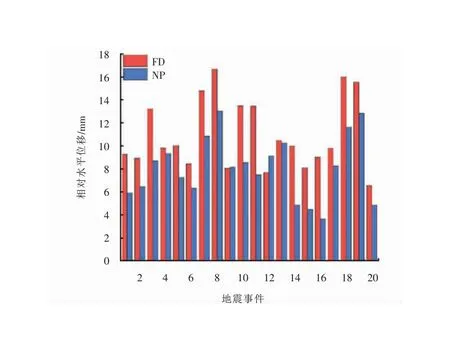
图9 20组FD和NP地震动的隧道相对水平位移响应

图10 单双向地震动作用下隧道变形图(放大50倍)

不论是FD地震动还是NP地震动作用下,竖向地震动输入对隧道结构位移响应的影响率分布都比较广,但处于±5%之内仍较多,相对来说对位移响应影响较大,结果如图11所示。水平向FD地震动下位移响应的竖向影响率分布在0附近多,比较窄而尖,这是由于存在脉冲的地震动对位移响应本身就更大,竖向地震输入造成的影响不太明显;而水平向NP地震动下位移响应的竖向影响率分布比较宽而矮,去掉脉冲部分的地震动对隧道位移响应明显要小很多,因此竖向地震的输入相对容易造成影响。

图11 竖向地震动输入对位移响应影响率

3.3 双向输入应力响应分析

单、双向地震动输入下PGV对隧道结构应力的影响如图12所示,从中可以看出,随着PGV的增大,应力响应也是不断增大的,单双向地震输入结果一致。

图12 单双向地震动作用下PGV对隧道应力影响

20组FD和NP地震动作用下隧道的应力响应关系如图13所示,FD地震动作用下的位移响应远大于NP地震动,得到的规律与上述一致。并且通过计算单、双向地震动作用下隧道结构最大Mises应力(MPa)以及脉冲影响系数和竖向地震动输入的影响率,可以发现竖向地震动的输入对隧道的应力响应对比于单向地震响应并不都是增大的,但是影响都是较小的,基本都在±5%之内,但是竖向输入对于水平向FD地震动的影响范围相对较广,如图14所示。

图13 20组FD和NP地震动的隧道底部加速度响应

图14 竖向地震动输入对应力响应影响率

4 结论

本文建立了隧道动力响应分析模型,选取了20组方向性效应脉冲地震数据,考虑竖向地震动与水平地震动共同作用下对隧道结构的影响,通过对比单向水平地震动作用的影响规律,得到如下结论:

1) 双向地震动作用下与单向地震动作用下对隧道结构有一致的规律,即随着PGV的增大,隧道的加速度、位移和应力响应都是增大的。

2) 通过对比FD地震动和速度脉冲处理得到的NP地震动对隧道结构的加速度、位移和应力响应的影响,发现FD地震动作用下的结构响应是远大于NP地震动作用下的,说明近场地震动中的速度脉冲会给结构带来巨大的危害,不可忽视。而现有规范都未考虑近断层脉冲地震的影响,因此在断层处进行施工设计时要将其纳入考虑因素,并且在加固的同时要设置柔性措施进行减震处理。

3) 双向地震动作用下相对于水平地震动作用下对隧道结构有一定的影响:通过竖向地震动输入影响率来表现,加速度响应和应力响应基本都在±5%之内,表明竖向地震动对其影响较小;而位移响应相对敏感,受竖向地震动的影响范围较广,但仍有大部分处于在±5%之内。主要原因是计算所选水平地震动PGA为0.3 g,相对较大,而竖向地震动对隧道结构的影响随PGA的增大而越来越小,但响应并非是一直增大。