基于MADDPG的多AGVs路径规划算法

尹华一，尤雅丽，黄新栋，段青娜

（1. 厦门理工学院计算机与信息工程学院，福建 厦门 361024；2. 厦门理工学院光电与通信工程学院，福建 厦门 361024；3. 红云红河烟草（集团）有限责任公司，云南 昆明 650000）

自动导引车（automated guided vehicle，AGV）作为搬运货物的主要角色，在实际的应用中往往需要多辆AGVs相互配合完成运输任务。在此过程中，每辆AGV按照一定的路径规划和作业要求，能够自主地行走、运输货物并停靠到指定的地点，具有极大的可靠性和灵活性。由于多AGVs被用于执行大规模且需要协作的任务，因此多AGVs的路径规划、任务调度等问题也成为研究热点。随着AGV的增多及环境复杂化，多AGVs的路径优化对提高物流系统的智能化和自动化也变得越来越重要，所以，开展多AGVs自主导航、避障的研究具有重要的意义。目前，关于路径规划的算法有很多，常见的有A*算法［1］、Dijkstra算法［2］、人工势场法［3］、快速扩展随机树算法（RRT）［4］、蚁群算法［5］、遗传算法［6］等，这些算法大多仅能求解单辆AGV 的路径规划问题，且容易受到环境因素的干扰，在多辆AGVs的环境下，处理大规模状态空间数据能力不足，难以收敛或者不稳定。

近年来，深度强化学习（deep reinforcement learning，DRL）结合深度学习（deep learning，DL）和强化学习（reinforcement learning，RL），实现了从原始输入到决策动作的端到端（end-to-end）的感知与决策。许多研究者将DRL 与路径规划相结合，如Meng 等［7］针对传统路径规划方法对地图信息的过度依赖以及缺乏自学习和自适应能力的问题，提出一种基于DQN 的单机器人路径规划方法；郭心德［8］通过ROS和Gazebo搭建智能仓储仿真环境，在DQN 算法的基础上提出基于Dueling DDQN-PER的单AGV 路径规划方法，使AGV 在复杂未知的环境中具有较高的路径规划成功率与较好的路径规划结果，但由于动作空间的限制只能将动作离散化，同时只适用于静态环境；Lei 等［9］为解决动态环境下路径规划问题，使用卷积神经网络对AGV 环境状态进行提取，并且将深度强化学习中的DDQN（Double DQN）算法应用在未知的动态环境中进行AGV 路径规划，让AGV 能够在离散的动作空间下实现动态避障到达目标位置；孟晨阳等［10］以栅格法搭建环境，改进基于深度确定性策略梯度（deep deterministic policy gradient， DDPG）算法的AGV 路径规划算法，结合ε-greedy 和波尔兹曼搜索策略更加有效地选择最优动作，引入优先级采样解决深度神经网络训练速度缓慢的问题；为了使DRL 适用于多智能体环境，Hu 等［11］研究集装箱自动化码头多辆AGVs 冲突预防路径规划，引入Gumbel-Softmax 策略对节点网络产生的场景进行离散化处理，通过MADDPG 算法来获得多辆AGVs 无路径冲突的最短路径。但现有研究成果存在以下不足：1）比起单辆AGV 相关问题的研究，针对多辆AGVs的研究过少。在多辆AGVs的环境中，每辆AGV的策略不仅取决于自身的策略和环境的反馈，同时还受到其他AGV 行为的影响。DDPG 等深度强化学习算法在单智能体的应用上表现优异，但是在多辆AGVs的环境下，算法适用性不强、收敛速度慢或者训练失败。2）关于多AGVs路径规划问题大多是针对静态环境展开的。但在动态的场景下，由于环境变化的不确定性，如何让AGV 规避障碍物稳定作业成为挑战。3）大多数智能算法将AGV 的动作离散化，即在固定速度的基础上，分为上、下、左、右等离散动作，或者是将速度和角速度离散化为固定的几个值来供选择。但在现实的环境中，AGV动作的控制量是连续的速度和角速度。

多智能体深度确定性策略梯度（multi-agent deep deterministic policy gradient， MADDPG）算法［12］在2017 年被提出，它采用了“集中训练，分散执行”框架，能够适用于传统强化学习算法无法处理的复杂多智能体环境，如多智能体协同合作场景和多智能体竞争对抗场景等。但MADDPG 算法在多AGVs 路径规划应用中，特别是在路径规划环境未知的情况下存在空白。为提高多AGVs 实时动态规划的能力，并弥补现有研究的不足，本文将深度强化学习中的MADDPG算法引入多AGVs环境中，设计出一种能够符合多AGVs环境特点的路径规划方法。

1 路径规划问题描述

1.1 环境建模

在货物运输环境中，多辆AGVs 之间需要通过协同合作来完成任务并且进行路径规划。在多AGVs路径规划环境（图1）下，二维平面环境中有多个货架、货物装卸点、障碍物、收发站和AGV。图中长方形图标代表货架，货物装卸点位置在货架中以深色正方形来表示，在货架与货架之间存在的障碍物以小正方形来表示，收发站位于最右侧以大正方形来表示，圆形图标代表AGV。

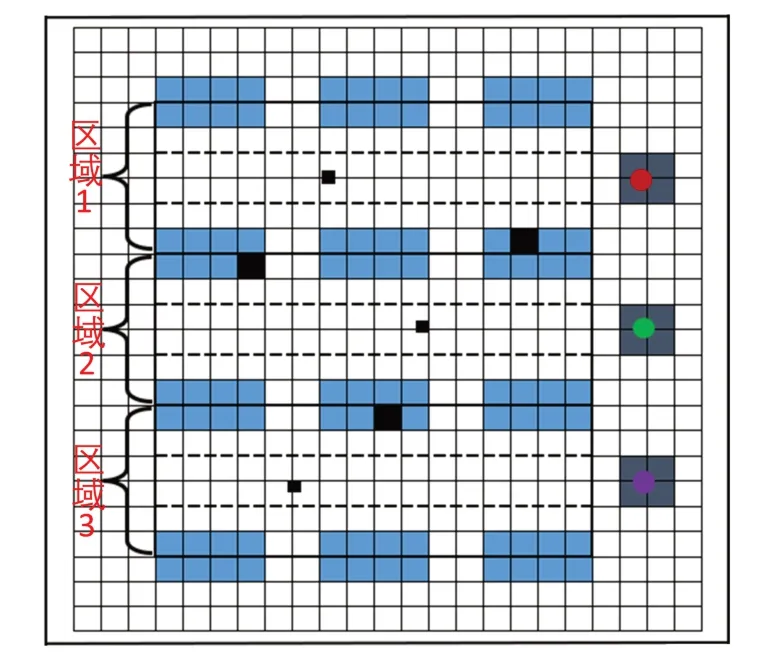
图1 多AGVs路径规划环境Fig. 1 Multi-AGVs path planning environment

本文设置的仿真环境为20 m× 20 m的智能仓储环境。为便于根据质点坐标来表示环境中物体的几何关系，实验时将环境范围缩放为2 × 2 的形式，质点坐标的取值范围为x∈[-1，1]，y∈[-1，1]。同时，为了方便确定物体的坐标和观察AGV 运动的轨迹，在二维平面环境中加入网格，每个网格的长度和宽度都为0.08，代表实际的0.8 m。在该环境中还需要考虑物体的长度和大小，因此对物体的质点进行膨化处理，预留安全边界，仿真环境中的物体模型如图2所示。

图2 仿真环境中的物体模型Fig. 2 Object model in simulation environment

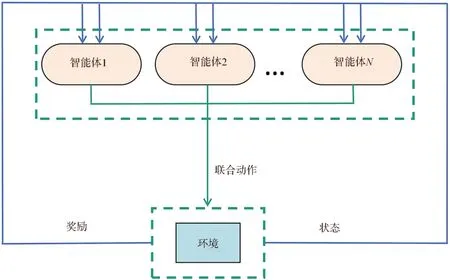
图3 MAMDP基本流程Fig. 3 MAMDP basic flow chart

1.2 路径规划

在实际的货物运输环境当中，AGV 的路径规划通常与任务分配相结合。AGV 的任务一般分为接收货物和卸载货物。本文主要考虑多辆AGVs从收发站出发，到达货架区域的货物装卸点去接收或卸载货物的过程。

在进行路径规划之前，作了以下的假设：

1）环境初始化时，已知AGV、障碍物的初始位置的范围和货物卸载点位置的范围；

2）每一回合，只考虑短时间内每辆AGV接收或卸载1个货物的路径规划问题；

3）AGV最大电池容量足以满足路径规划的能量消耗，不至于中途停下；

4）不考虑AGV出环境边界的问题。

每一回合环境初始化时，货架、收发站的初始位置是固定的，而AGV 的初始位置、障碍物位置和货物装卸点在货架中的位置则会更新，因此，需要知道AGV、障碍物初始化时位置的范围和货物装卸点位置的范围。AGV 初始化时，位置坐标在收发站的范围内；障碍物初始化时，位置坐标在图1中虚线框起来的区域内；为了考虑实际需求的合理性，将货物装卸点位置在货架中的分布范围作区分，3 个货物装卸点的位置分别位于3 个可选择区域的货架中，且每个AGV 对应1 个货物装卸点（如图1 所示）。在整个仿真环境中，AGV 还会避免与静态障碍物（货架、障碍物）和动态障碍物（其他AGV）相碰撞。

在进行多AGVs路径规划时，需要考虑AGV所在的环境。环境可以分为静态环境和动态环境，环境的不同在一定程度上决定了AGV 路径规划决策的方法和难度。所在环境可分为两种情况：1）在进行路径规划之前就已经知道了所有的环境信息。包括AGV 初始位置、货物装卸点位置、障碍物位置、货架位置等都已被提前探测到，且不会发生改变。这类环境是静态环境，对于AGV 路径规划来说是最简单的，也是目前研究最为成熟的。2）在进行路径规划之前，只知道部分固定的环境信息，还有一部分环境信息没有被探测到。这需要AGV 一边进行路径规划一边探测。这类环境就是动态环境。本文主要针对第二种情况进行路径规划，设置货架、收发站为固定的环境信息，AGV 初始位置、货物装卸点位置、障碍物位置会随着每一回合环境的初始化而改变，且在每一回合中，对于当前AGV来说，其他AGV 在环境中也是动态变化的。在动态环境中，AGV 会根据其他AGV 位置、障碍物位置和货物装卸点位置的不同来规划路径。

在本文研究的实验场景中，多辆AGVs规划合理的路径从收发站的不同位置出发，在避免碰撞的情况下，规划出靠近货物装卸点位置的路径。

2 基于MADDPG的多AGVs路径规划算法的模型设计

2.1 多智能体马尔科夫博弈过程（MAMDP）

在多智能体深度强化学习环境中，智能体遵循多智能体马尔科夫博弈过程（MAMDP）［13］，基本流程如图 3 所 示 。 MAMDP 通 常 可 以 用 多 元 组来表示，具体含义如下：S为全局环境的状态空间；N为环境中智能体的数量；ai(i= 1，…，N)为当前智能体的动作空间；所有智能体的联合动作空间可用A=a1× …×aN表示；ρ：S×A×S′ →[0，1]为联合状态转移函数，即智能体在执行联合动作A后，促使环境状态发生转移，ρ表示从当前状态s∈S到下一状态s′ ∈S′的概率分布，概率分布范围为[0，1]；ri(i= 1，…，N)为当前智能体的奖励函数；γ∈[0，1]为奖励的折扣因子。

在多智能体马尔科夫博弈过程中，智能体将各自的动作ai(i= 1，…，N)以联合动作A的形式输入到环境中，与环境进行交互之后将环境状态从S变为S′并得到反馈，反馈的内容包括整体的状态和整体的回报；之后每个智能体从整体的状态和整体的回报中得到自己的状态和回报，重新输出各自的动作并且将以上的过程不断迭代更新。智能体能够与环境交互，通过试错和奖励机制发现最佳策略［14］。而智能体的奖励与状态转移相关，状态转移又受到联合动作的影响。可以使用Actor-Critic 框架，来获取多智能体的最优联合策略［15］。

2.2 MADDPG算法模型

MADDPG 算法是一种常见的多智能体深度强化学习（MDRL）算法，是对单智能体深度强化学习算法中的DDPG算法在多智能体环境下的扩展。该算法采用了“集中训练，分散执行”框架，能够适用于传统强化学习算法无法处理的复杂多智能体环境，如多智能体协同合作场景和多智能体竞争对抗场景等。

在MADDPG 算法中，每个智能体都拥有自己的策略网络（Actor）、评估网络（Critic）和经验缓存池，相对于传统的Actor-Critic 算法，MADDPG 算法中智能体的数量为N，智能体i的动作为ai，观测信息为oi。在训练阶段，智能体i的Critic 网络为(S，a1，a2，…，aN)，其中S=o1，o2，…，oN，该Critic网络的输入不仅包含了智能体i自身的观测信息和动作，还包含了其他智能体的观测信息和动作；而在执行阶段，智能体i的Actor 网络为μθi(oi)，其中θi为Actor 网络的网络参数，该Actor 的输入仅根据当前智能体的观测信息来更新自身的策略ai，即ai=μθi(oi)。因此，这种Actor-Critic 网络框架采用了“集中训练，分散执行”原则，即在训练时使用全局信息包括所有智能体的状态和动作，在执行时只使用智能体自己的局部信息。

算法的整体框架如图4所示。

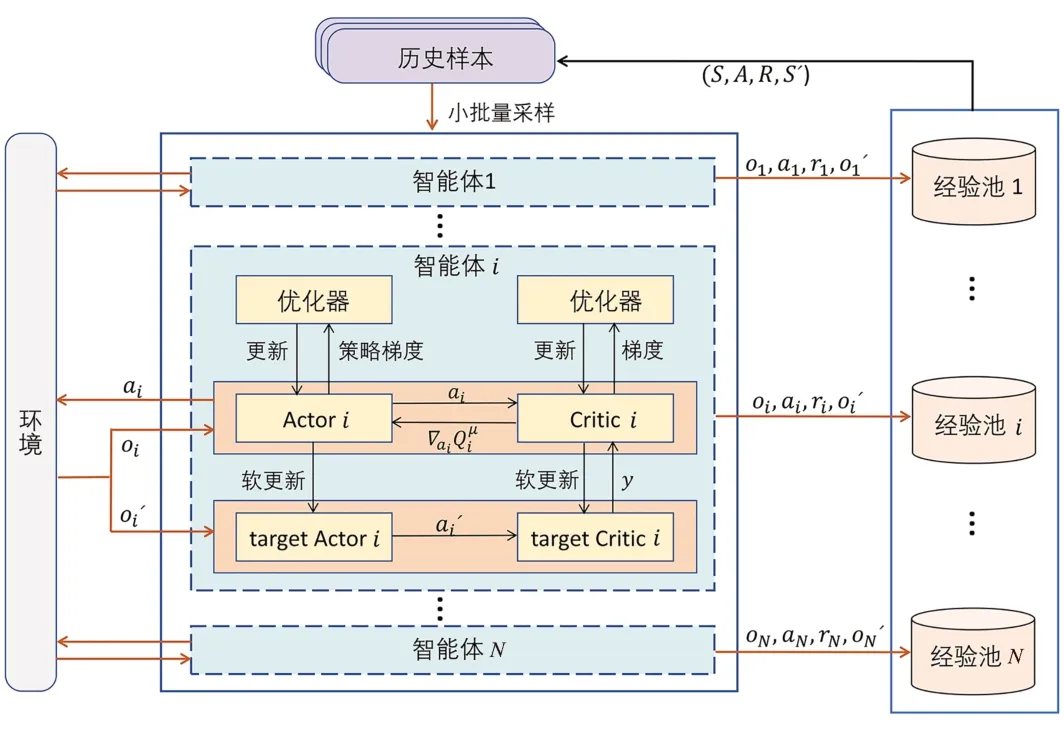
图4 MADDPG算法框架Fig. 4 MADDPG algorithm framework

对于单个智能体i，将其状态输入到自身的Actor 网络中，Actor 网络会进行策略探索得到该智能体的动作，动作与环境交互得到新的状态和奖励，最后将该智能体的状态、动作、新的状态和奖励作为经验放入自身的经验池中。所有的智能体都会与环境进行不断的交互，并且将得到的经验不断地存储到各自的经验池当中。在更新当前智能体的网络之前，会从每个智能体的经验池中抽取出同一时刻的数据，从而得到新的经验(S，A，R，S′)存入到经验池D中，再以小样本方式从D中随机采样多个(S，A，R，S′)训练各自的神经网络，这样就能够降低经验间的关联度，并且能够重复利用过去的经验。在经验(S，A，R，S′)中，S=o1，o2，…，oN，包含了所有智能体在同一时刻下的状态；A=a1，a2，…，aN，是在同一时刻下做出的动作集合；S′ =o′1，o′2，…，o′N，是相同时刻下动作A与环境交互后得到的新状态；R=r1，r2，…，rN，是所有智能体从环境中得到的回报值。Critic 网络会对Actor网络的策略进行评价，确定动作的有效性，即将S和A作为当前智能体i的Critic网络输入，得到评价值。

当前智能体i除了策略网络、评估网络以外，还有目标策略网络（target-Actor）和目标评估网络（target-Critic）。将o′i∈S′输入到当前智能体i的target-Actor网络中得到动作a′i=μ′i(oi)，并将S′和A′作为输入传到target-Critic网络中，得到下一时刻的值。

MADDPG算法通过随机梯度下降更新每个智能体的Actor网络，计算公式为

式（1）中：∇θiJ(μi)是Actor网络确定性策略μi(ai|oi)的回报期望梯度，D是经验池，(S，a1，…，aN)为Critic网络的评价值。

Critic网络由最小化损失函数来进行迭代更新，其计算公式为

式（2）~（3）中：L(θi)为Critic 网络的最小化损失函数；y为目标值；(S′，a′1，…，a′N)为target-Critic网络的评价值；μ′i(o′i)为target-Actor网络的策略；ri为动作奖励值；γ是奖励的折扣因子。

目标网络参数值更新为

式（4）中：为target-Critic 网络的参数；为Critic 网络的参数；θ′i为target-Actor 网络的参数；θi为Actor网络的参数；τ为调整更新频率的控制参数。

2.3 多AGVs路径规划算法模型

基于OpenAI Gym 环境接口搭建二维仿真环境用作多AGVs 的训练平台，该平台可以更好地适用于本文所关注的多AGVs路径规划决策问题。在有多辆AGVs参与的协作过程中，需要对多辆AGVs设计状态空间、动作空间和奖励函数。

环境中共有N辆AGVs，分别为AGV1、AGV2、…、AGVN。在MADDPG 算法中，对于第i辆AGV的状态除了自身状态SAGVi外，还包括了其他AGV 的状态SA和环境状态Senv。SAGVi中含有当前时刻下AGVi的速度(υAGVi，x，υAGVi，y)和位置坐标(PAGVi，x，PAGVi，y)；为了体现AGVi与其他AGV 的位置关系，状态SA表示为(∆PAGVi1，x，∆PAGVi1，y，…，∆PAGVij，x，∆PAGVij，y)，其中j=N- 1代表其他AGV 的个数；环境状态Senv含有K个障碍物的位置坐标，以及N个货物装卸点位置与N辆AGVs 的位置关系，其中，K个障碍物中第i个障碍物的坐标表示为（Hi，x，Hi，y），N个货物装卸点位置中第i个装卸点位置的坐标与第i辆AGV的坐标差为(∆Pii，x，∆Pii，y)， 因此，Senv表示为(Hi，x，Hi，y，…，HK，x，HK，y，∆Pii，x，∆Pii，y…，∆PNN，x，∆PNN，y)。

对于第i辆AGV在t时刻下的状态定义为：

AGV 的动作是每一时刻给予AGV 在水平方向（x） 和竖直方向（y） 上的瞬时速度（υAGVi，x，υAGVi，y），动作的取值范围为：υAGVi，x∈[-1，1]、υAGVi，y∈[-1，1]，因此动作空间是一个二维的连续空间。根据当前AGV 的状态输入，在MADDPG 算法中会得到一个确定性的动作策略，即确定的速度，那么AGV经过∆t时刻后，位置更新为（，），具体的表达式为

奖励函数既和每辆AGV 的动作有关，又和整体AGV 的行驶状况相关，因此，一个符合实际需求的奖励函数对策略的影响是极大的。将于第i辆AGV在t时刻下的奖励定义为

奖励函数的含义如下：

1）AGV 碰到货架（视为静态障碍物）：AGV 在行驶的过程中是不允许碰到货架的，因此设置一个碰到货架的负奖励Rh，当AGV的位置坐标在货架坐标的区域里，那么Rh=-1，否则Rh= 0。

2）AGV 碰到障碍物（视为静态障碍物）：在环境中设有障碍物，该障碍物可以看作是物体或者静止不动的人，AGV 在行驶的过程中需要避开这些障碍物防止碰撞，因此设置一个碰到障碍物的负奖励Rz，当AGV 与障碍物之间的距离小于Dz，Rz=-1，否则Rz= 0，Dz为障碍物与AGV 之间的最小安全距离。

3）AGV 间碰撞（视为动态障碍物）：AGV 与AGV 之间应该保持安全距离、避免碰撞，为了避免AGV 之间的距离过近从而发生碰撞，因此需要设置一个碰撞奖励Rp，当AGV 之间的距离小于安全距离Dd（Dd为两辆AGVs的半径之和），则设碰撞奖励为Rp=-1，否则Rp= 0。

4）装卸货物奖励：在本文的设计中，每辆AGV 需要去货架区域完成对应的货物装卸任务，为了引导AGV 接近货物装卸点的位置，设置一个距离奖励Rr，Rr=-d11- …-dNN，即每一时刻计算每辆AGV 与对应的货物装卸点位置的距离，并且取负值作为奖励，距离越近，奖励越大，当距离小于0.12时，再给予更大的奖励使AGV 加速靠近货物装卸点位置，Rr=-d11- …-dNN+ 0.4 ×n，其中n为距离值小于0.12的AGV的个数。

基于MADDPG 算法模型以及对多辆AGVs状态空间、动作空间和奖励函数的设计，提出如图5所示的多AGVs路径规划算法架构。

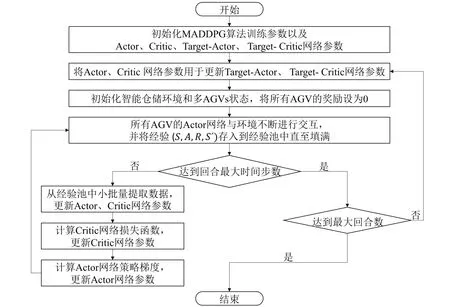
图5 基于MADDPG的多AGV路径规划算法架构Fig. 5 Frame of multiple AGVs path planning algorithm based on MADDPG

3 实验结果及分析

3.1 实验参数设置

本文重新设计了MADDPG 算法的网络结构，策略网络的网络结构是［20；96；96；2］的全连接神经网络；价值网络的网络结构是［66；96；96；1］的全连接神经网络，隐藏层采用ReLU 函数作为激活函数。MADDPG 算法的神经网络结构具体如图6所示。

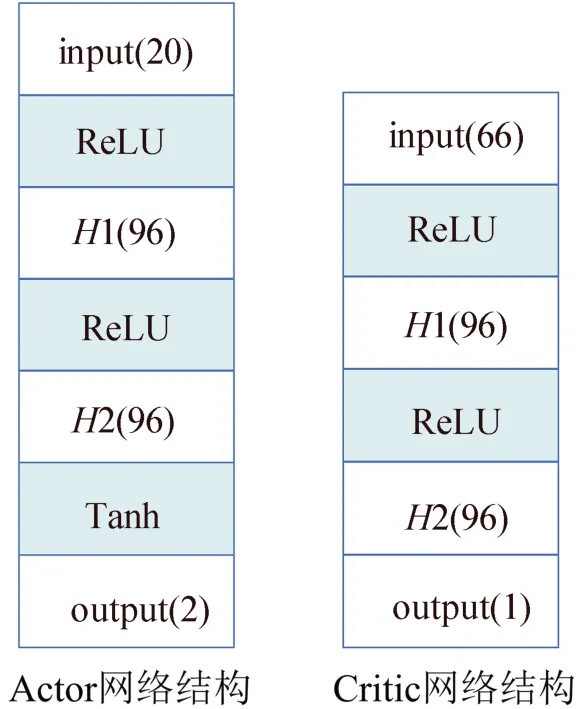
图6 MADDPG算法的神经网络结构图Fig. 6 Neural network structure diagram of MADDPG algorithm

为了验证MADDPG 算法解决多AGVs 路径规划问题的有效性，需要初始化仿真环境后进行测试，并将测试结果与DDPG 算法、TD3 算法进行对比。仿真环境参数的设定如表1 所示。为方便描述物体在质点坐标下的几何关系，在实验中将20 m × 20 m 的智能仓储仿真环境范围缩放为2× 2 的表示形式，同理，将AGV 小车的半径0.3 m 等比缩放为0.03，具体的路径规划规则在第一节中做了详细的介绍. 同时，设置25 个时间步长为1 个回合episode，当超过25 个时间步长时将结束路径规划，并重新初始化仿真环境开始下一回合。

表1 仿真环境参数设置Table 1 Simulation environment parameter settings

本文参考文献［12］，设置了如表2所示的训练参数。

表2 MADDPG训练参数设置Table 2 MADDPG training parameter settings

3.2 实验结果分析

将MADDPG 算法与DDPG 算法、TD3算法在同一仿真环境下进行比较，通过平均回报值来评估算法性能的优劣，即平均回报值越大，多AGVs的路径规划就越好。

图7 为3 辆AGVs 经过60 000 回合训练后得到的平均回报曲线图。其中横坐标表示训练的回合数episodes，纵坐标表示平均回报值（以1 000 回合为1 个间隔单位计算3 辆AGVs 的总体奖励均值）。根据实验数据可知，MADDPG 算法、DDPG算法和TD3算法的平均回报值最后都取得了收敛的效果。训练开始时3 辆AGVs 的平均回报值比较小，这说明AGV 的路径规划策略是不合法的，随着训练回合数的增加，平均回报值也在不断地增加，直到收敛到一个较稳定的值，这说明在之后的训练中AGV 学到了比较好的路径规划策略。对于MADDPG算法、DDPG 算法和TD3 算法的训练效果，可以得到两个结论，一是MADDPG 具有更快的收敛效果；另一是MADDPG 算法的平均回报值显然是优于DDPG 算法和TD3 算法的，具有更好的收敛效果。两个结论都证明了MADDPG算法的优势。

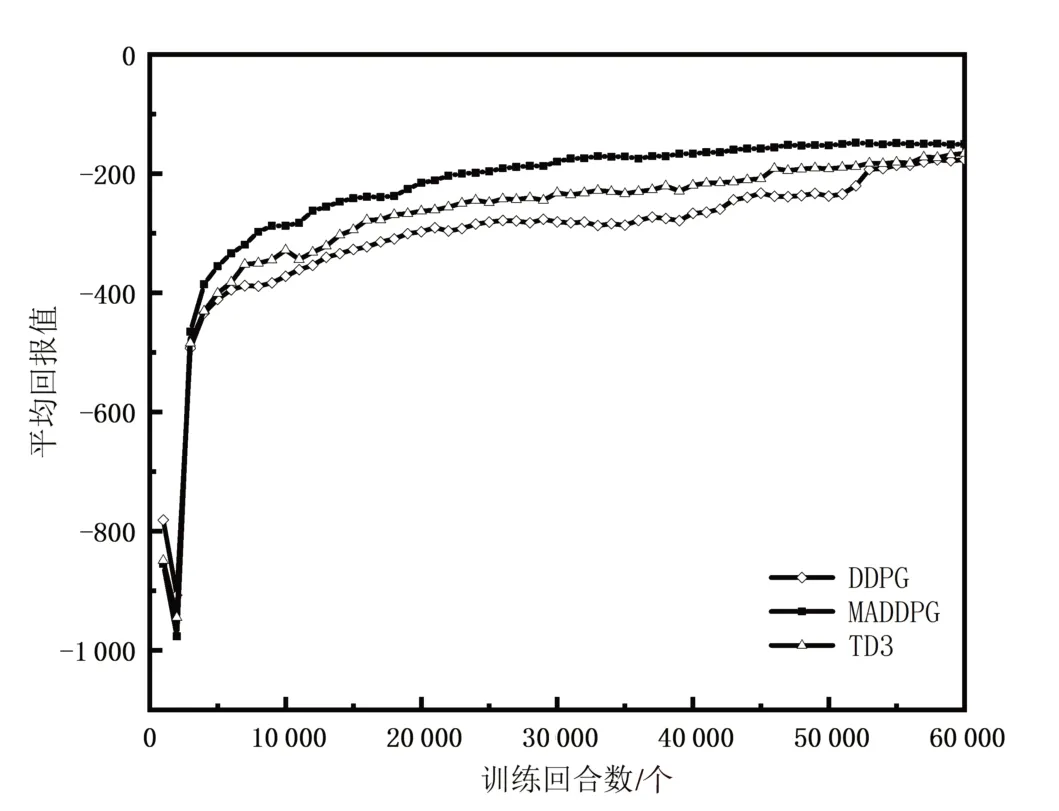
图7 3种算法的平均回报值曲线对比Fig. 7 Comparison of the average return curve of three algorithms

为了进一步验证本文所设计的算法在多AGVs路径规划环境中的使用效果，对仿真环境进行1 000次初始化。每次初始化时AGV的初始位置、障碍物位置和货物装卸点位置都会更新，选取多AGVs间相互碰撞次数、多AGVs碰到货架次数、多AGVs碰到障碍物次数和是否到达货物装卸点作为算法的性能评价标准，并将训练后的算法模型加载到对应的智能体中，测试结果如表3所示。

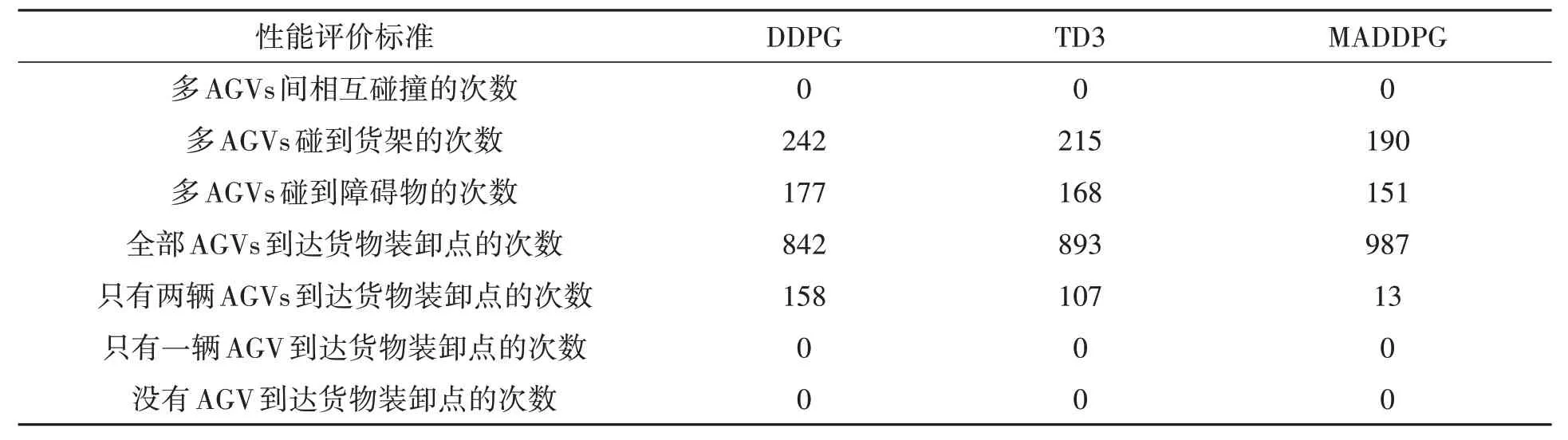
表3 3种算法在多AGVs路径规划场景中的测试结果（1 000回合）Table 3 Test results of three algorithms in multiple AGVs path planning scenarios (1 000 episodes)

由表3 可知，相较于DDPG 算法和TD3 算法，本文所提的MADDPG 算法的性能更加优越：多AGVs碰到货架的次数分别减少了21.49%、11.63%，多AGVs碰到障碍物的次数分别减少了14.69%、10.12%，全部AGVs到达货物装卸点的次数分别高出了17.22%、10.53%。这里的到达货物装卸点指的是AGV的质点落在货物装卸点前的那一个网格正方形中。

为了直观地展示算法的路径规划能力，本文将规划能力较弱的DDPG 算法与MADDPG 算法进行对比，多AGVs路径规划轨迹（任意一个回合的仿真环境）具体如图8所示。从图8可见，在DDPG算法对应的图中并不是所有的AGVs 都靠近了货物装卸点，如第1 个AGV（红色圆形图标）相对货物装卸点1还有一定的距离，并且第2个AGV（绿色圆形图标）还会碰到障碍物；而在MADDPG算法对应的轨迹图中，所有AGVs 都靠近了货物装卸点，并且没有碰到障碍物、货架或其他AGV。总体而言，基于MADDPG算法的多AGVs路径规划能力较强。

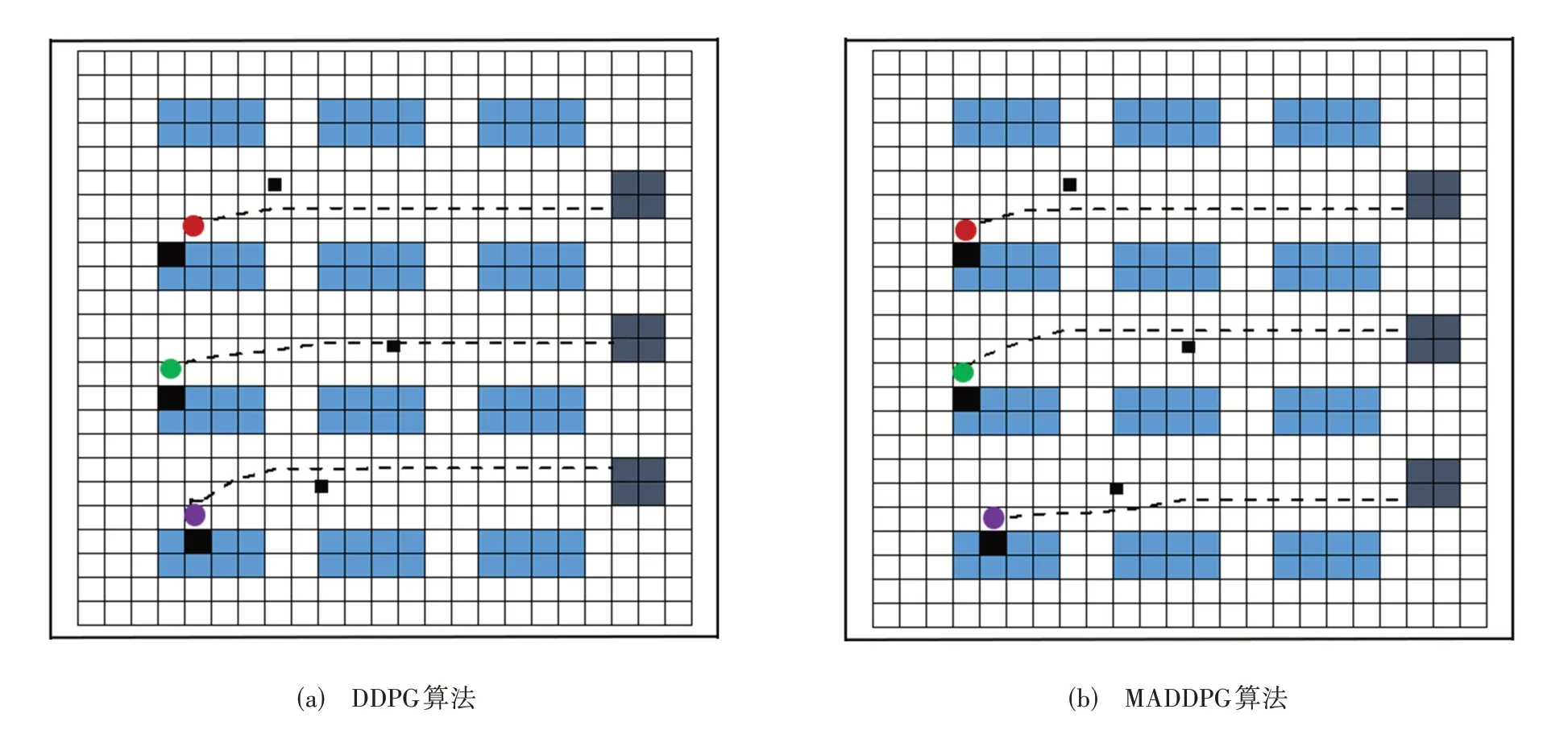
图8 DDPG、MADDPG算法的多AGVs路径规划Fig. 8 Multiple AGVs path planning based on DDPG and MADDPG

4 结论

针对多AGVs 在动态不确定环境下完成货物运送并进行路径规划的问题，本文开展了基于MADDPG 算法的多AGVs路径规划研究，通过状态空间、动作空间、奖励函数和网络结构重新设计了MADDPG 算法的模型结构，并开发二维仿真环境用作多AGVs 的训练平台。实验结果表明，基于MADDPG 算法的多AGVs路径规划能够在动态不确定环境下具有较高的自适应能力，该算法所规划的路径能够避开各种障碍物并靠近货物装卸点，解决了多AGVs 路径规划决策问题。相较于DDPG 和TD3算法，本文提出的MADDPG 算法的性能更加优越：多AGVs碰到货架的次数分别减少了21.49%、11.63%，多AGVs 碰到障碍物的次数分别减少了14.69%、10.12%，全部AGVs 到达货物装卸点的次数分别高出了17.22%、10.53%。本研究为多AGVs 的路径规划问题提供了一种新的求解思路，但在实践中，每辆AGV可能对应多个货物装卸点，因此，未来的工作将聚焦于多AGVs对多目标任务路径规划上，以实现更加智能化、实用化的多AGVs路径规划算法。