基于IST-RSCKF-MB的雷达多目标跟踪算法

李艳玲，方 遒，屠亚杰

（厦门理工学院机械与汽车工程学院， 福建 厦门 361024）

目标跟踪技术被广泛应用于自动驾驶和视频监控等领域。在自动驾驶领域中，利用目标跟踪技术可以及时感知车辆环境变化，从而降低事故发生率。车载毫米波雷达目标跟踪主要是对行驶车辆、行人等目标进行跟踪，且目标具有机动性强和灵活性高的特点。随着毫米波雷达分辨率的不断提高，车载毫米波雷达的应用将呈现多样化［1-3］。

车载毫米波雷达多目标跟踪算法的计算主要为非线性系统近似和数据关联两方面。受限于车载毫米波雷达的测量原理［4］，车载毫米波雷达目标跟踪采用非线性卡尔曼滤波算法对目标进行距离和速度估计，典型算法有扩展卡尔曼滤波器（extended Kalman filter， EKF）、无迹卡尔曼滤波器（unscented Kalman filter， UKF）和容积卡尔曼滤波器（cubature Kalman filter， CKF）。刘华军等［4］提出快速平方根CKF算法，简化预测阶段的状态和协方差阵计算，提高了运行效率和跟踪精度。戴雪梅等［5］提出强跟踪平方根CKF 算法，目标状态突变时仍能保持对目标的跟踪能力，减少了运行时间。传统数据关联算法［6-8］是基于关联概率的组合方法，郑丹阳等［9］提出变分推断的联合概率数据关联（JPDA）算法，解决JPDA 算法的组合爆炸问题，但通过优化方法解决变分问题没有将数据关联的计算量降至较低范围。蒋凯等［10］提出改进强跟踪无迹卡尔曼的交互式多模型联合概率数据关联（IMM-JPDAISTUKF）算法，提高了距离和速度的跟踪精度，但交互式多模型算法需已知各模型的概率转移矩阵，JPDA 算法存在较大的计算量，UKF 算法在强非线性系统表现为较低的跟踪精度。传统数据关联算法有较大的计算量，只适用于特定场景。而基于随机有限集的数据关联算法［11-14］可以有效避免复杂的关联计算问题，还可以动态地表示目标与量测数量的变化。张昱等［15］提出多模型高斯混合概率假设密度（MM-GMPHD）算法，提高了防撞雷达预警系统的可靠性，但基于高斯假设的高斯混合概率假设密度（GMPHD）算法仅适用于线性运动目标，应用于车载毫米波雷达时跟踪精度较低。张强等［16］提出高斯混合-势概率假设密度（GM-CPHD）算法，能有效抑制杂波和稳定地估计目标状态及目标数量，但计算复杂度高。王海环等［17］提出均方根容积卡尔曼序贯蒙特卡罗概率假设密度（SCK-SMC-PHD）算法，有效抑制经典序贯蒙特卡罗概率假设密度的粒子退化问题，但序贯重要性采样方法具有较大的计算量，适用性窄。综上所述，雷达多目标跟踪算法的非线性系统近似与数据关联两方面具有较大的计算量。本文提出改进强跟踪平方根容积卡尔曼多伯努利的雷达多目标跟踪算法，将改进渐消因子的强跟踪（IST）引入快速平方根容积卡尔曼滤波（RSCKF）中，联合多伯努利（multi-Bernoulli，MB）算法进行多目标跟踪，以解决多目标跟踪算法计算量大的问题。

1 算法的实现

1.1 IST-RSCKF算法

考虑如下的非线性离散系统

式（1）中：Xk和Zk分别为系统k时刻的状态向量和k时刻的量测向量；Fk为k时刻的状态转移矩阵；h为量测的非线性函数；wk和vk为k时刻互不相关的高斯白噪声序列，其协方差矩阵分别为Qk和Rk。

RSCKF算法基于三阶球面-径向容积准则选取容积点和权值，容积点ξi和权值wi表示为

式（2）中：[1]=[In，-In]，m= 2n，m表示容积点数，是状态维数n的2 倍，In表示n维的单位矩阵，[1]i表示[1]的第i列。快速RSCKF算法步骤如下。

步骤1：初始化。初始化状态向量Xk，k、误差平方根协方差矩阵Sk，k、过程噪声Qk和量测噪声Rk。

步骤2：时间更新。计算系统在k+ 1时刻的预测状态和平方根协方差矩阵分别为

式（4）中：Tria(⋅)为矩阵的三角化运算；SQ，k为Qk的平方根，SQ，k=Qk。

步骤3：量测更新。计算系统在k+ 1时刻的状态向量和误差平方根协方差矩阵分别为

式（5）中：为状态预测值；Kk+1为增益；z为量测值；为量测预测值。式（6）中：X*和Z*为互协方差参数；SR，k为量测噪声协方差。式（5）和式（6）相关参数的计算式为

针对非线性系统，强跟踪理论上需进行3次采样完成一次滤波。第一次采样针对状态方程，计算预测状态值和预测误差协方差阵。第二次采样针对量测方程，计算预测量测值、量测误差协方差阵和互协方差阵。根据第二次采样结果计算渐消因子和引入渐消因子后的预测误差协方差阵。第三次采样根据预测误差协方差阵计算预测量测值、量测误差协方差阵和互协方差阵，进而更新状态值和误差协方差阵来完成一次滤波过程。考虑式（1）的非线性系统，状态方程采样简化为一般卡尔曼滤波形式。根据量测方程进行第二次采样计算预测量测值、量测误差协方差阵、互协方差阵和渐消因子，量测更新结果通过第二次采样结果与渐消因子的简单计算获得。因此，ISF-RSCKF 算法仅针对量测方程采样，在一定程度上减少了计算量。在式（13）计算完成之后计算渐消因子，有

式（17）~（18）中：tr(⋅)为矩阵求迹运算；Hk表示量测更新获得雅可比矩阵；Vk为实时输出残差序列的协方差矩阵；上标T为矩阵转置。相关参数计算为

式（19）中：(⋅)-1为矩阵求逆运算。式（20）中：ek=zk-为每次滤波新息；ρ表示遗忘因子，通常取ρ= 0.95。根据文献［18］改进渐消因子的方法，其λk、Nk和Mk在快速RSCKF的表达如下

量测更新中获得平方根协方差矩阵后，根据式（13）计算渐消因子λk。计算引入渐消因子的互协方差矩阵、平方根协方差、增益和量测更新的雅可比矩阵，相关参数的计算式为

量测更新式为

式（27）：I为同维度的单位矩阵。

1.2 MB算法

在多目标跟踪过程中，因目标的新生、消失和继续存在引起目标状态和数量的动态变化，使得传感器获得量测数量也发生变化，可采用随机有限集描述多目标跟踪过程中目标状态变化和量测变化。基于共轭属性的多伯努利混合（MBM）算法［14］可采用单个目标的后验分布表示整个后验分布，避免时间更新和量测更新的复杂积分问题。因MBM 算法在整个滤波过程中的全局假设数量为L个，每次均与下一时刻的量测值进行关联，导致该算法存在较大的计算量。许多学者致力于研究获得一个全局假设的方法来减少计算量［19-20］。本文提出使用新息自相关矩阵和Murty 算法［21］共同确定最佳假设的多伯努利（MB）算法。MB 算法滤波过程与MBM 算法滤波过程类似，主要在Murty算法执行后引入新息自相关矩阵选择此次滤波的最佳假设。新息自相关矩阵是目标与测量值的误差自相关矩阵，选择新息自相关矩阵迹的较小者且为全局假设中的关联假设作为此次滤波的最佳假设。最佳假设索引流程如图1所示。图1中，V0为每个目标与量测的自相关矩阵，Opt_index为全局假设。

图1 索引流程图Fig. 1 Index flowchart

1.3 ISF-RSCKF-MB 算法

通过在数据关联和非线性系统近似两方面进行改进以减少目标跟踪算法的计算量。将改进渐消因子的强跟踪思想引入快速平方根容积卡尔曼滤波中形成IST-RSCKF 算法，并联合MB 算法进行多目标跟踪。ISF-RSCKF-MB算法步骤如下。

步骤1：初始化。初始化k时刻多目标状态，目标被探测的概率Pd和存活概率Ps。

步骤2：时间更新。k时刻多目标状态由IST-RSCKF 算法的时间更新完成，其他时间更新参数可参考文献［14］。

步骤3：量测更新。为避免大量计算，利用马氏距离将步骤2中的预测状态值与量测值进行分组，不属于多目标组内的量测判为杂波，无需进行更新。预测状态值未与任何量测分为一组，属于漏检目标；预测状态值与某个量测分为一组，属于目标关联到测量。k时刻多目标状态由IST-RSCKF 算法的量测更新完成，其他量测更新参数可参考文献［14］。

步骤4：确定滤波假设。根据多目标权值构建代价矩阵作为Murty算法的参数，Murty算法输出的全局假设与新息自相关矩阵共同确定最佳假设。计算每个目标的新息自相关矩阵迹的最小值的关联假设，查找存在于Murty算法全局假设中的关联假设作为最佳假设，删除其余全局假设。

步骤5：强跟踪量测更新。根据步骤4获得的最佳假设计算渐消因子，k时刻多目标状态由引入改进渐消因子的IST-RSCKF算法的量测更新完成。

步骤6：计算目标跟踪算法的评价指标。采用广义最优子模式分配（GOSPA）度量［22］评价目标跟踪算法性能。

步骤7：修剪伯努利项。移除最佳假设中不存在的伯努利项。

2 实验结果与分析

2.1 实验场景及评价指标

实验采用TI公司的AWR1843BOOST和DCA1000EVM 采集行人轨迹数据，毫米波雷达可用带宽为4 GHz，其他实验参数设置如表1所示。

表1 雷达数据采集参数设置Table 1 Parameter settings for radar data acquisition

实验场景为常见的水泥路面，行人轨迹范围为：x1=-4 m，x2= 4 m，y1= 2 m，y2= 30 m，行人以近似匀速的速度远离雷达，其初始状态分别为X1= [1，2，0，0]，X2= [0，2，0，0]，X3= [-1，2，0，0]。建立匀速模型（CV）的运动方程和量测方程（式29）进行实验。

式（29）中：R为径向距离；x为横向坐标；y为纵向坐标；θ为方位角；vr为径向速度；ẋ为横向速度；ẏ为纵向速度。

本文采用GOSPA 度量评价车载毫米波雷达多目标跟踪算法性能，包括位置误差、漏检误差和误检误差［23］。即有

2.2 仿真实验

图2 是关于数据关联的GOSPA 误差对比，将改进强跟踪平方根容积卡尔曼分别结合MB算法和MBM 算法进行多目标跟踪。表2 为改进强跟踪平方根容积卡尔曼多伯努利混合（IST-RSCKF-MBM） 算法与本文算法的GOSPA 误差。由图2 可知，上述2 种算法的GOSPA 整体误差趋于12.247 4 以下，表明能有效跟踪目标。由表2可知，本文算法的误检误差小于IST-RSCKF-MBM 算法的误检误差，漏检误差小于IST-RSCKF-MBM 算法的漏检误差，表明所提MB 算法能改善数据关联欠佳的问题。与IST-RSCKF-MBM 算法相比，本文算法的GOSPA误差减少4.71%，表明Murty算法与新息自相关矩阵共同确定最佳假设方法有效。IST-RSCKF-MBM 算法与本文算法耗时依次为5.507 1、3.656 3 s。

表2 2种算法的GOSPA度量误差Table 2 GOSPA errors by the two algorithms

图2 2种算法的GOSPA误差比较Fig. 2 Comparison of GOSPA errors of the two algorithms

将改进渐消因子［18］的强跟踪思想引入简化的平方根容积卡尔曼滤波中，联合MB 算法称为IST-RSCKF-MB2算法。图3是关于系统模型的GOSPA 误差对比，分别为平方根容积卡尔曼多伯努利（RSCKF-MB） 算法、ISTRSCKF-MB2 算法和本文算法的GOSPA 误差。表3 是RSCKF-MB 算法、IST-RSCKF-MB2 算法和本文算法的GOSPA 误差。由图3 可知，以上3 种算法的GOSPA 整体误差趋于12.247 4以下，表明算法能有效跟踪目标。由表3 可知，与RSCKF-MB 和IST-RSCKF-MB2 算法相比，本文算法的GOSPA 误差分别减少0.36%和1.99%，表明改进渐消因子计算方法能有效减少系统模型误差。RSCKF-MB 算法、ISTRSCKF-MB2 算法与本文算法耗时依次为3.843 1、4.139 6和3.656 3s。

表3 3种算法的GOSPA度量误差Table 3 GOSPA errors by the four algorithms

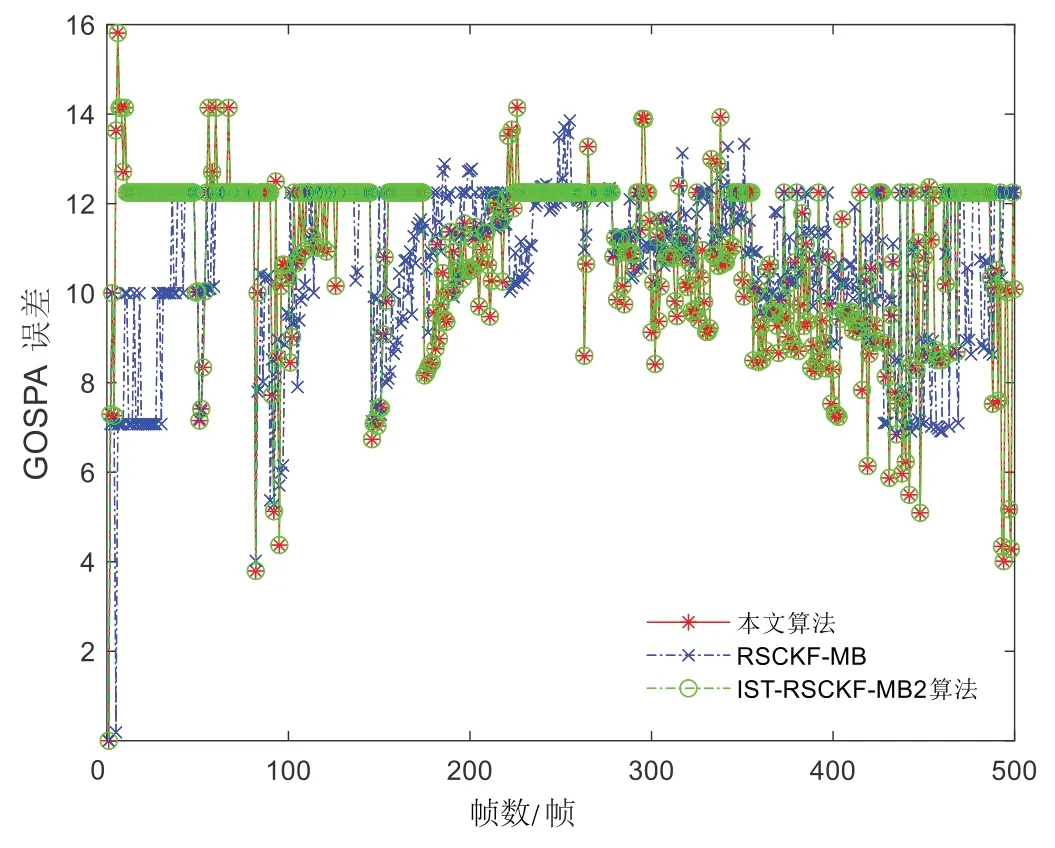
图3 3种算法的 RMS-GOSPA总体误差比较Fig. 3 Comparison of RMS-GOSPA errors of the three algorithms

图4 为无迹卡尔曼多伯努利（UKF-MB）算法、扩展卡尔曼多伯努利（EKF-MB）算法和本文算法的GOSPA 误差对比，表4 为EKF-MB、UKF-MB 和本文算法的GOSPA 误差。由图4 可知，EKF-MB 算法的GOSPA 误差在200 帧之前围绕12.247 4 波动，在200帧之后整体趋于12.247 4 以上，表明EKFMB算法不能有效跟踪目标；UKF-MB算法的GOSPA 误差在200 帧之前逐渐增加，在200帧之后围绕12.247 4 波动，表明UKF-MB 算法不能较好地跟踪目标；本文算法的GOSPA整体误差趋于12.247 4 以下，表明能较好地跟踪目标。由表4 可知，与EKF-MB 和UKFMB 相比，本文算法的GOSPA 误差分别减少14.75%和0.17%，即本文算法提高了多目标跟踪精度。EKF-MB 算法、UKF-MB 算法与本文算法耗时依次为6.800 8、5.466 8 和3.656 3 s。

表4 3种算法的GOSPA度量误差Table 4 GOSPA errors by the three algorithms

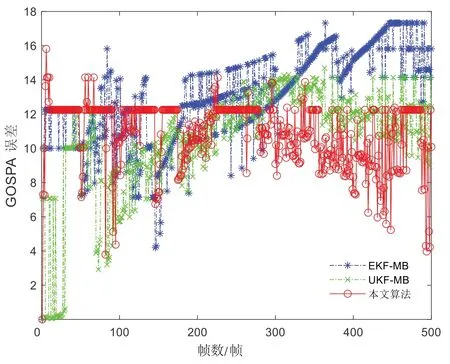
图4 3种算法的GOSPA误差比较Fig.4 Comparison of GOSPA errors by the three algorithms

3 结论

本文提出改进强跟踪平方根容积卡尔曼多伯努利的雷达多目标跟踪算法，将改进渐消因子的强跟踪引入简化的平方根容积卡尔曼滤波中，并联合MB 算法进行多目标跟踪。结果表明，所提算法的GOSPA 误差与平方根容积卡尔曼多伯努算法、改进强跟踪平方根容积卡尔曼多伯努利混合算法、扩展卡尔曼多伯努利算法和无迹卡尔曼多伯努利算法相比分别减少0.36%、4.71%、14.75%和0.17%。本文算法耗时最少，提高了雷达多目标跟踪精度，可推进基于随机有限集的算法在实际工程中的应用。