基于连续可微采样的无人机多向视点规划

吴 华,徐肖顺,白晓静

(华北电力大学 控制与计算机工程学院电力智能机器人工程技术研究中心,北京 102206)

0 引言

针对室外物体表面缺陷的巡检,主流方式为逐点拍摄式自主巡检。以风机叶片巡检为例,无人机搭载光学传感器沿风机叶片以固定距离飞行并拍照采集可见光影像。但绕飞叶片拍摄方式耗时较长、耗能较大,无人机在单次起降时间内可巡检的设备量少,巡检效率低。这是因为室外对象的全覆盖巡检时间与巡检对象模型表面结构的复杂度呈正相关,形成了飞行巡检作业的效率瓶颈,制约短航时微型无人机在大范围巡检中的推广应用。因此,本文提出一种结合机载云台与相机传感器特性的最优拍摄多向视点规划方法。本方法在保证视图采集质量前提下,通过减少拍摄航点数量和增加单航点在多个方向的拍摄次数,降低航点转移时高能耗的空中位移运动,从而有效地提高巡检飞行的采集效率。

本文的主要贡献如下:

(1)提出了一种视图质量指标来衡量视点的拍摄效果,并将这一指标与视点几何约束相结合,提出了连续可微的目标函数并给出求解算法。

(2)提出了多向视点的求解算法,使得单个航点不再只生成单个方向的采集视点。

(3)通过实验评估了在不同巡视对象模型的条件下,本文所提方法在降低了77%以上的航点数量的同时保证了100%覆盖率和良好的拍摄质量。

1 研究现状

视点规划的研究方法可大致划分为两类:①将视点规划问题看作全覆盖路径规划问题[1-8],这类方法通过规划能够覆盖整个观测区域的路径来解决视点规划问题;②“生成与验证”的方法[9],其中“生成”是指运用策略在算法初期生成大量的初始候选点,“验证”是通过组合优化方法从初始的候选视点中选择满足约束条件的视点子集。

解决全覆盖路径规划问题的算法主要专注于优化确保覆盖范围和飞行安全的最短路径。一般的工作将全覆盖路径规划问题视为画廊问题(Art Galley Problem,AGP)和旅行商问题 (Traveling Salesman Problem,TSP)。这使得该问题在多项式时间内很难求解。BIRCHER[1]提出一种结构检查计划器(Structural Inspection path Planning,SIP),SIP根据模型的几何形状在一组预定义的搜索空间内对可行的视点进行采样,并通过迭代优化视点间的最短路径重新采样视点,但该方法限制了传感器的自由度,对于结构复杂的物体,并不能完全覆盖,同时,该方法仅优化路径长度,并未考虑拍摄质量。JUNG[4]等人提出一种多层规划的方法(Multi-Layer Coverage Path Planner,ML-CPP)将待巡视模型体素化,然后分为多个层级,从第一层开始逐层规划视点,每轮迭代通过计算上一层视点的覆盖范围更新下一层视点位置,最后求解全局TSP问题连接所有层级的视点,该算法相比于SIP算法减少了视点数,优化了无人机飞行时间,但仍存在较多的视点数,并且未考虑视图质量。SHANG[5]受SIP的视点采样策略的启发,提出一种协同优化算法(Co-optimal Coverage Path Planning,CCPP),增加了一个自由度,使用粒子群算法同时优化视图质量与最短路径来进行重采样,该方法解决了SIP的部分缺陷,但其仍以规划路径任务进行视点规划,视点数量仍未得到减少,巡检效率低。此类算法通过限制无人机的运动空间或者自由度,以最佳覆盖巡检路径为优化目标来求解。而对于巡检飞行而言,较多的视点数量会显著降低巡检效率。

“生成与验证”算法[9]分为两步计算:第一步生成大量候选视点,第二步采用智能算法策略选出合适的一组结果视点。其中,第一步中的视点采样方法分为空间采样、顶点采样和面片采样3种。①空间采样方法[10-12]首先通过给定参数和模型定义一个采样空间,在采样空间中采集一批候选视点,用待巡检对象模型辅助优化和评估候选视点。②顶点采样[13-14]方法依赖于对象模型,启发式抽取模型顶点后进行采样,从顶点往外取景深范围内的距离处为视点位置。ZHOU等[16]提出一种新的前沿信息结构来描述目标对象的空间信息,将目标对象进行聚类,划分为不同组的前沿信息结构,以每组前沿信息的中心点为球心,均匀采样视点,再以覆盖率为评价指标筛选视点。③面片采样[15]首先将对象模型划分为面片,其中曲面拆分为多个子面片,计算每个面片的可视边界,最后将候选视点沿最大边界的法线放置在固定距离处。PRIETO[16]将三维模型离散化为体素,将曲面分割为简单子面片,并为每个面片找到可行视点。MOSBACH[17]使用B样条曲线和一组特征泛函分析测量对象的几何特征,并使用它们来指导采样过程。由于空间采样并未构造解析表达式,无法对视点位置进行微分,很难在视点规划中有效寻优。顶点与面片采样方法中每个生成的视点只关注其局部的模型几何信息,因此无法保证结果视点集的全局最优。第二步的筛选视点的方法如Sampling-based[18],Medial-objects[19],基于测量不确定度的方法[20]等通过构建可见性矩阵,采用启发式智能算法如粒子群优化(Particle Swarm Optimization,PSO)算法等在保证覆盖率的同时对视点位置进行筛选。这类方法的视点依赖生成的候选视点集,因此初始的候选视点集的生成方式决定了最终视点集的质量。

已有研究忽略了云台自由度和视觉传感器特性,使每个航点仅生成一个拍摄方向,而实际上无人机搭载云台在同一个航点可以凭借其偏航与云台俯仰实现多方向的拍摄。尽管每悬停一个航点拍摄多张照片所需时间略长于单次拍摄的时间,但是由于总体航点数显著减少,采用该方法能显著降低飞行能耗并提升巡检效率。此外,鲜有研究工作在视点评价指标上考虑巡检任务所关注的视图采集质量。针对上述问题,本文提出一种新的连续可微多向视点规划算法(Multi Directional View Point Planing,MD-VPP),通过连续视点采样模型的数学表示,以巡检对象在相机内成像质量和最小化航点数量为目标,得到收敛的全局最优结果,既能满足巡检对象巡视覆盖率与拍摄质量要求,又能大幅降低飞行能耗。

2 方法

2.1 视点采样建模与优化

本文通过模型结构面片的可见约束形成视点采样空间,其中要为待巡检面片中的每个三角面片选择一个视点。为了计算更优的视点位置,采用了迭代重采样方案。计算上一轮采样视点对所有待巡检面片的可见质量的导数,以梯度下降的方式进行重采样。

2.1.1 视点的几何约束采样

在空间位姿模型中,视点有6个自由度。其中包括3个自由度的空间位置参数(x,y,z)和3个自由度的姿态角参数(ω,φ,γ) (φ为俯仰角,ω为偏向角,γ为翻滚角)。考虑实际飞行中无人机云台的固有特性,无人机的云台滚转角由无人机自行调节,其相对于世界坐标系的偏差接近于零。因此,多旋翼无人机在巡检过程中的视点由位置、偏航角和俯仰角组成,可定义为g(x,y,z,ω,φ)。考虑到本文中的巡检对象是基于三维网格模型表示,首先为网格模型中每一个面片采样初始视点。

对于某个视点,其位置信息为g=[x,y,z]。g受到最小有效拍摄距离dmin,最大有效拍摄距离dmax,和最小入射角的约束。如图1a所示。

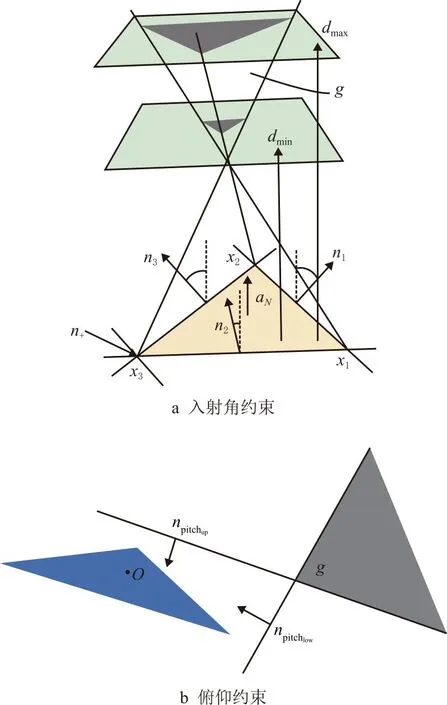
图1 入射角与俯仰约束示意图

由于云台自身有一定的俯仰范围,视点还受到最小俯仰角为ψmin,最大俯仰角为ψmax和视场(Field of View,FOV)的约束。如图1b所示。综合得到的视点采样的空间约束如下:

(1)

式中xi表示三角形面片的顶点;aN表示三角形面片归一化的法向量;ni表示入射角的分割平面的法向量;O表示三角面片几何中心;npitchup表示最大俯仰角分割平面的法向量;npitchlow表示最小俯仰角分割平面的法向量;nfov表示FOV分割平面的法向量。

2.1.2 视点的投影质量约束

计算每个三角面片在影像传感器上的投影,最大化面片投影在成像平面的面积来评定视点的巡视质量。为确保寻优过程可微,本文创新地改进了非线性的投影目标函数。假设面片在相机坐标系下,光心距离面片几何中心O的距离为d,与面片单位法向量aN的夹角为θ,进行正交投影之后,三角面片原始面积Sorin投影至成像平面,成像平面的面积Scam与原始面积的关系:

(2)

可知式(2)关于d与θ(定义域[0,90°])均单调递减。因此本文最终讨论得到每个视点gj采样的优化目标函数可以间接转换成如下目标函数:

(3)

(4)

由isVisible(i,j)可以建立视点关于面片的可见性矩阵A。由d与θ可建立所有采样视点与所有面片之间的投影质量矩阵B。因此,最终视点采样优化函数可写为:

minf=-A·B,

(5)

其中,每一轮中的第j个视点gj的梯度算子如式(6):

∇fj(x,y,z)=

s.t.isVisible(i,j)=True。

(6)

因此,可以使用目标函数的全微分∇f快速得到最大投影面积的寻优方向,从而求解得到满足投影质量要求的视点位置并将视点放入候选视点集中。

2.2 基于覆盖率的候选视点选择

通过寻优采样得到候选视点后,进行视点的评定,以减少视点数量。此时,目标函数最小化视点数量的同时应满足视点的覆盖率是否达标,优化目标函数可写为:

(7)

A·x≥γ。

其中:x=[x1,x2,…,xi,…,xn]T,xi表示第i个视点是否被选择,被选择为1,不被选择为0;n为候选视点集视点个数;γ为覆盖率,巡检任务中设为100%的覆盖率,从而保证结果视点集中的视点对所有面片可见。

综上可知,上述集合覆盖问题可以采用如贪心算法、遗传算法等来解决。本文使用贪心搜索算法来解决集合覆盖问题。

算法流程(如图2)如下:

图2 算法流程图

输入:模型待巡检面片集P,面片个数n,FOV大小,安全距离dmin,最大距离dmax,俯仰角范围φlow～φup。

1.迭代:

2.当i≤n:

由第i个面片构建第i个视点的采样空间。若为第一轮,则在采样空间中随机初始化视点位置,V←vi;否则遍历面片集P,构建第i个视点的可见性矩阵Ai。计算可见质量在上一轮位置的微分,沿梯度下降方向偏移视点位置。

3.迭代结束,退出循环。

4.得到候选视点集V,在候选视点集中采用贪心搜索策略进行筛选。

5.建立未被覆盖面片集Puncover,初始化Puncover=P。

6.当Puncover≠Ø:

计算对Puncover集的覆盖率,选择V中覆盖率最大的Vresult←vi

从V中删除vi,从Puncover中删除视点vi可见的面片

7.直到A·x>=γ

8.得到结果视点集Vresult

输出:结果视点集Vresult。

3 实验与分析

为验证所提MD-VPP方法的性能,本文采用风机以及公开模型如:solarPlant、Big ben、hoaHakanaia等进行实验。将本文的MD-VPP与SIP、CCPP、ML-CPP等优秀方法进行了对比,并在算法和实验中充分考虑到工业巡检中最常见的无人机数据采集配置,如:无人机可进行-180°～ 180°的全向偏航、云台在-120°～ 30°范围内的俯仰运动。通过航点数减少率作为一个核心指标评定各类算法。实验结果表明,本文提出的MD-VPP方法不但在计算得到的航点数减少率、多方向拍摄能力和覆盖率上显著优于其他方法,而且也能够获得理想的拍摄效果。

3.1 视点规划结果

图3展示了采用MD-VPP方法在FOV=60°条件下的视点规划结果。由于风机叶片姿态会产生变化,针对风机模型,本文采用3种特殊的风机姿态模型,分别对其进行视点规划实验。

图3 航点空间位置三维可视化及与观测面片间的关联关系

如图3所示,红点代表航点位置,右图中的连线代表每个航点对应面片的视线。相同航点的视线采用同种颜色着色。结合表1所知,在风机模型中,图3a风机倒Y型停机时,在覆盖所有面片的条件下得到8个航点,航点集中于下方两个叶片周围;图3b风机叶片存在水平姿态时,在覆盖所有面片的条件下得到8个航点,航点集中于水平方向的叶片周围。这是一种很特殊的姿态,因为存在水平方向的叶片,而云台仰视角有限,需要从较偏的视角去拍摄。仅采用沿着叶片规划航点的方法是无法巡检这类姿态的叶片。图3c所示风机正Y型停机时,在覆盖所有面片的条件下可通过9个航点实现,航点集中于上方两个叶片周围。图3d所示solarPlant模型,在覆盖所有面片的条件下可通过3个航点实现。图3e所示BigBen模型中,在覆盖所有面片的条件下可通过23个航点实现。图3f所示hoaHakanaia模型中,在覆盖所有面片的条件下可通过12个航点实现。如图3a～图3c所示,叶片朝地面的面片空间区域集中有较多航点,是因为当模型中存在较多面片法向量朝下时,而云台的仰视角度受限,需要从较偏的视角去拍摄,形成了更多的航点聚集于此。此外,视点采样可微性使得算法迭代计算更新视点后保留了最优的候选视点集,同时最优的候选点集上的覆盖约束要求确保仅用少量航点即可覆盖所有面片。因此,从实验结果可以明显看到本方法可以极少的航点采集得到完整的数据。

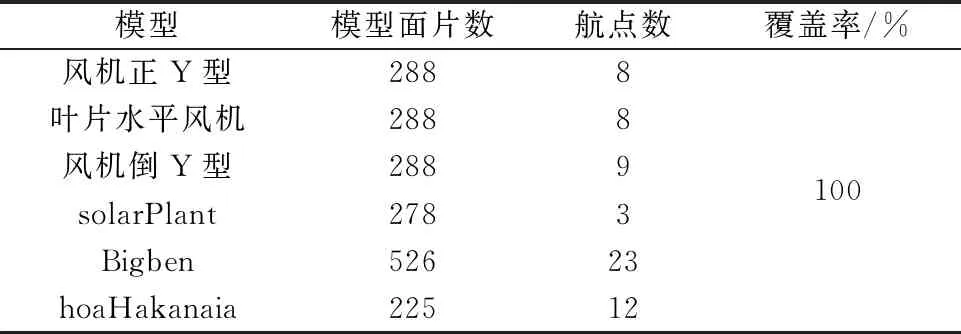
表1 MD-VPP算法计算各模型全覆盖巡视的航点数及其覆盖率

为进一步对比本文方法优势,表2给出了MD-VPP与以SIP为代表的可微分迭代重采样方法、以优化视点数量为目标的ML-CPP方法、将投影质量纳入目标的CCPP等3种优秀方法在航点数及覆盖率上的结果,并给出了MD-VPP方法规划的航点数相对于其他方法的航点数减少率(由式(7)给出)。结果表明,本文方法不但在覆盖率上优于其他方法,并且相对其他优秀方法至少降低约77%以上的航点数量。

(7)

表3对视点规划领域中优秀方法与MD-VPP进行了定性的对比。其中,SIP和ML-CPP等方法缺失俯仰自由度时,对于几何结构复杂的模型,不能求解全覆盖的视点。表3中除本方法外的其他方法均为单一航点生成单一的视点,这些方法规划得到的航点数量远多于MD-VPP规划所生成的航点数量。因此,MD-VPP以极少的航点数显著降低了飞行的能耗,从而有效地提高了巡视效率。此外,SIP[1]、Sampling-based[18]、Medial-objects[19]、ML-CPP[4]、Targetted sampling[11]、改进栅格法[15]、FUEL[14]和Near-Optimal 3D[8]均未将拍摄质量纳入视点规划的目标函数中,所规划的视点无法保障目标成像质量。CCPP虽然考虑了拍摄质量,但其目标函数不可微,CCPP采用改进的粒子群算法粒子数为N,面片数为M,则计算复杂度约为O(MN),而本文提出的拍摄质量目标函数单轮迭代中可微,可在一个视点位置沿最快方向下降优化,计算复杂度约为O(M),效率高于CCPP中不可微目标函数的求解方式。综上可知,本文提出的MD-VPP算法既保证了视图质量,也优化了航点的数量。

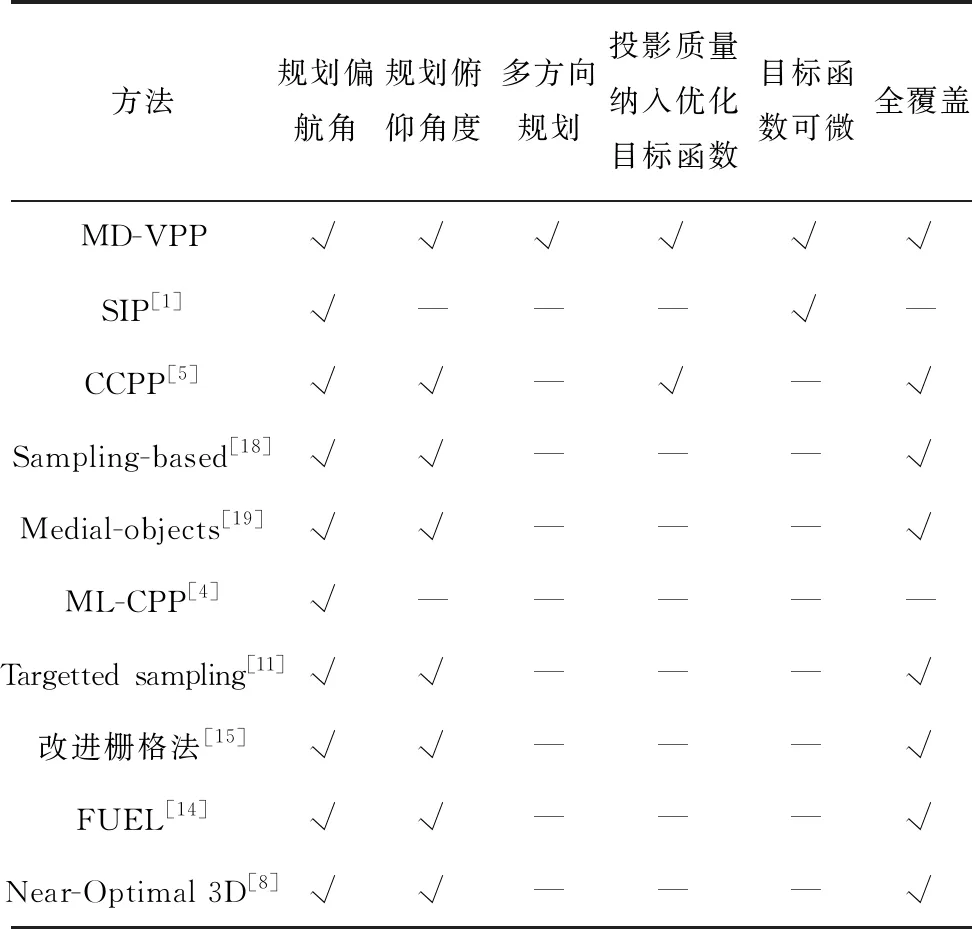
表3 代表性方法对比

3.2 3D仿真软件实验结果

本文在Blender 3D软件中模拟无人机空中巡检采集风机外观影像数据,并选择FOV为60°时的视图数据为代表,通过图4展示了航点位置和视线,并将其结果在Blender中进行验证,由图5展示部分代表性航点位置在Blender中验证得到的影像结果。

图4 风机巡视航点位置与其视点-面片3D空间对应关系

图5 风机水平叶片时MD-VPP规划的航点位置所采集的代表性图片序列

将迭代优化4轮与迭代优化12轮后规划的结果在Blender 3D软件中模拟采集风机外观影像数据,验证了MD-VPP算法可用少量的航点采集优质成像质量的图片。对于图4所示姿态下的风机叶片,MD-VPP算法规划的航点仅8个,且航点中视点所覆盖的面片以不同颜色连线表示出来。选择这个停机角度的风机模型,是因为当前业内通过规划沿叶片飞行拍摄航点的方式在叶片水平时将失效,即需人工调节无人机航点位置以在云台俯仰角度限制范围内拍摄到叶片。采用MD-VPP算法进行规划,代表性结果如图5a所示,展示了迭代优化12轮后在航点5拍摄的叶片图像,仅用少量航点即可覆盖水平方向叶片朝下侧的视图采集。此外,图5b和图5c展示了迭代优化4轮和迭代优化12轮后航点1的采集的其他叶片的视图,迭代优化12轮相比于仅迭代优化4轮得到的航点采集的图像中叶片占比更大。结合图6航点可见质量迭代曲线可知,MD-VPP算法有效提升了航点的观测质量。通过图5a～图5c中各视点拍摄的图片可见,即使存在特殊姿态的面片,规划得到的每个航点上的不同视点的拍摄质量并未降低或失真,且无需人工干预规划,仍可以完整地覆盖被观测模型所有面片。同时,在求解过程中,将巡视质量纳入目标函数中共同参与优化视点,得到满足成像质量的图片。

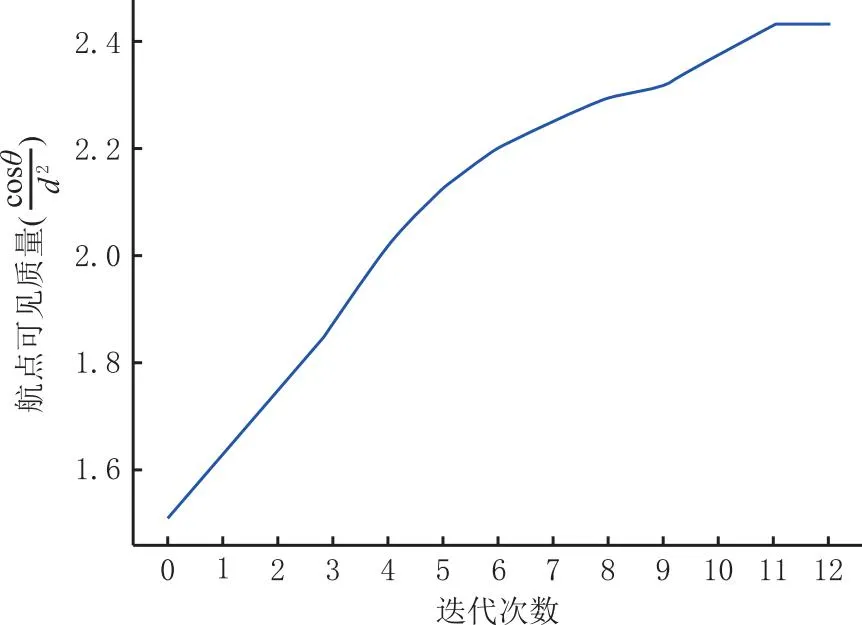
图6 风机水平叶片时MD-VPP航点可见质量迭代曲线

上述实验结果表明,本文提出的MD-VPP算法不但在航点数量上显著优于现有国内外优秀算法计算得到的航点数,而且通过可微的设计,确保了寻优过程的效率,从而进一步保证了巡视质量。此外,对于特殊的模型结构,也能够有效结合自身传感器约束,求解得到满足硬件参数限制的航点和有效的拍摄图像。

4 结束语

本文提出一种全新的连续可微多向视点规划算法——MD-VPP。首先,通过连续视点采样模型的数学表示得到收敛的全局最优解。其次,采用可微的投影质量数学表达形式,从而保证了在视点寻优中有效调整巡视质量的梯度方向,从而生成最佳候选视点集合。最后,将可见性信息编码为可见性矩阵,将问题表示为覆盖集问题,采用贪心搜索算法进行求解得到最优视点。MD-VPP与同类先进方法相比,能够求解得到极少的航点,并保证覆盖度和拍摄质量,航点数至少能减少77%以上。综上所述,MD-VPP求解过程可微,提升了视点寻优的效率;航点数量极低,提高了巡检作业的效率;同时在多种拍摄参数约束下的拍摄覆盖度和质量良好。因此本方法具有良好的理论创新意义和工程应用价值。实际应用中,除了可见光传感器,无人机还可携带其他不同类型的传感器对工业设备进行巡检。未来研究将探索各类传感器协同巡检,进一步提高无人机巡检的可靠性和效率。