基于深度学习的多孔材料渗透率预测研究进展

钱 淼 ,周 骥 ,向 忠,王嘉琦 ,魏鹏郦,李 俊

(浙江理工大学 浙江省现代纺织装备技术重点实验室,浙江 杭州 310018)

0 引言

目前,多孔材料在科学技术与工业界得到了普遍应用,已然成为一个机械、数学、信息等跨学科研究载体[1-4]。渗透率作为其重要特性,受到了国内外不同领域学者的关注[5-11]。

多孔材料渗流现象一般通过达西定律进行描述。在小雷诺数条件下,渗透率可以利用压降和流速通过达西定律计算出来,压降和流速可以通过实验或者数值方法得到。现今,基于先进的传感器,压降和流速的测量精度不断提高,所得到的渗透率也愈加准确[12]。

已有的基于大量实验数据统计分析得到的多孔材料结构参数-渗透率的经验公式,可用于快速预测渗透率[13],如Kozeny-Carman方程、Ergun方程等。然而,实验数据拟合方法需要耗费海量的时间和费用。而数据集少又会导致所建立的经验公式欠拟合、泛化能力弱。

随着计算机技术的发展,机器学习技术得到了应用。结合机器学习的多孔材料渗透率快速预测方法被不断地提出,一些学者利用支持向量机(Support Vector Machine, SVM)、随机森林(Random forest)以及决策树(Decision tree)等传统机器学习算法构建了渗透率回归预测模型[14-16]。近年来,基于深度学习的多孔材料渗透率预测建模方法更受国内外学者的关注,相比于传统机器学习方法具有更强的非线性拟合能力,所建立的渗透率预测模型也具有更好的预测精度[17],成为当前的研究热点。

利用深度学习技术构建多孔材料渗透率快速预测模型主要分为结构模型生成、渗透率获取以及渗透率快速预测建模三大步骤。其中,渗透率获取一般使用格子玻尔兹曼(Lattice Boltzmann Method, LBM)、孔隙网络模型(Pore Network Model, PNM)以及有限体积(Finite Volume Method, FVM)等传统方法,本文不进行叙述,而重点针对多孔材料结构模型的生成、渗透率快速预测模型的建立等关键问题,系统综述深度学习技术在多孔材料渗透率预测建模领域的研究进展。

1 多孔材料结构模型生成方法

高质量结构模型的生成是使用数值方法研究多孔材料微观及宏观流动性能的前提。模型生成方法主要分为两类:①正向建模法,主要通过计算机辅助设计或参数化建模等方法直接生成多孔材料结构模型,如单元建模法[18]、三周期极小曲面建模法[19-20]等,此类方法主要用于多孔材料结构设计,难以重构自然界中复杂孔隙的多孔结构模型;②逆向重构法,广泛用于生成随机多相材料结构模型,主要包括实验重构法、表征重构法以及深度学习重构法。

实验重构法具有精度高、与真实结构匹配性好的优点,但获取的图像大概率会存在噪声,需要进行细致的前处理工作,难以短时间内重构出大量的模型样本。表征重构法可重构与真实多孔材料具有相似统计表征信息的结构模型[21]。深度学习重构法主要利用数据集训练深度学习模型后重构新的多孔材料结构模型。本文主要介绍表征重构法和深度学习重构法。

1.1 表征重构法

目前,多孔材料结构模型表征重构(Characterization and Reconstruction, C&R)方法已成为一个较为成熟的技术领域,主要包含结构统计表征和重构两个步骤。结构统计表征是指对多孔材料的形态结构进行统计量化的过程。随机多孔材料难以进行确定性的特征描述,一般是通过统计相关函数[22](两点相关函数等)和物理描述符[23](孔隙率、孔径等)等进行表征。重构是指基于有限的表征信息,利用智能优化算法等方法生成多孔材料结构模型。

一种最直接的表征重构方法就是利用物理描述符直接进行结构模型重构。在选定一个或一组物理描述符后计算目标图像对应的值,然后随机生成一个初始图像,通过不断地调整使其物理描述符对应的值等于或接近目标图像,不断调整的过程通常可以借助优化算法(如模拟退火、遗传算法等)进行[24-26]。另一种直接重构方法是四参数随机生长法(Quartet Structure Generation Set, QSGS)[27],其中4个参数分别为固相分布概率、方向增长概率、概率密度以及孔隙率。该方法可以通过设定方向增长概率控制生成结构模型的各相同性或异性。

但是,物理描述符仅仅只是一阶统计量,表征信息量不足,使得重构模型与真实模型的匹配性差。例如:具有相同孔隙率的不同多孔材料可能会表现出完全不同的力学或流动传输性能。解决该问题的一种办法就是使用更高阶的统计量进行模型重构。

JOSHI[28]提出了高斯随机场(Gaussian Random Fields, GRF)重构法,使用标准的一点(孔隙率)以及两点相关函数信息重构各向同性的两相性材料。GRF方法以二维岩心切片的统计信息为基础,首先产生一个由相互独立的高斯变量组成的高斯场,然后通过线性变换使其具有相关性,最后通过非线性滤波器进行阈值分割生成最终的重构模型。QUIBLIER[29]进一步优化该算法,实现了三维多孔材料结构模型的重构。但是,GRF重构法难以扩展合并其他统计函数,且难以重构出多相和各相异性多孔材料结构模型。

YEONG等[30]构造了一种包含多个统计相关函数的目标能量函数,并详细阐述了基于模拟退火算法的一维和二维结构模型重构步骤。后续一些学者又将模拟退火重构法扩展至三维结构模型重构[31-32]。

曲线几何拓扑结构很难使用两点统计函数进行重构,而是需要进行参数化描述或同时考虑更多的点。因此,学者们提出了多点统计法(Multiple-Point Statistics, MPS),其核心思想是某一点的状态仅由少数邻域点决定[33]。马尔可夫链-蒙特卡洛(Markov Chain Monte Carlo, MCMC)方法属于MPS方法[34]。该方法使用2点及5点邻域模板对原始多孔材料二维切片图像进行遍历,得到邻域模板每种配置的条件概率,然后利用蒙特卡洛算法确定重构图像中每点的状态(孔隙或固相)。WU等[35]又引入15点以及19点邻域模板实现了三维多孔材料结构模型的重构。

1.2 深度学习重构法

近年来,深度学习技术与多孔材料研究领域的结合不断加深,已有大量学者对深度学习重构方法进行了研究。BOSTANABAD等[36]提出一种基于马尔可夫假设的监督学习重构方法,将随机多孔结构建模为一个平稳马尔可夫随机场,然后通过决策树算法基于训练图像学习一个目标像素对邻域/特定像素的条件概率模型,最后通过该模型重构出新的图像。与多点统计法不同的是,该方法训练出了一个条件概率模型,重构新样本的计算效率相对更高。BOSTANABAD等[37]又将该方法从二维扩展至三维,使其能够用于3D结构模型重构。

监督学习重构方法需要预先引入马尔可夫假设,较难用于处理复杂的材料系统[38]。近年来,通过学习可观测数据的概率密度而随机生成样本的深度生成模型受到人们的广泛关注,成为研究热点。许多学者将不同的深度生成模型应用在多孔结构的重构中,如深度信念网络(Deep Belief Networks, DBN)[38-39]、变分自动编码器(Variational Autoencoders, VAE)[40-41]、生成对抗神经网络(Generative Adversarial Nets, GAN)[42-44]及相关混合模型[45-46]等。

DBN网络由于训练时需要有标签的数据集以及学习过程较慢等原因在多孔材料重构领域应用较少。VAE在原来自动编码器(Auto-Encoder, AE)的基础上引入变分推断和重参数化技巧,使编码后的潜向量呈高斯分布,然后使用解码网络将该高斯分布的潜变量映射为新的图像。VAE的目标函数为真实分布对数似然函数的证据下界(Evidence Lower BOund, ELBO),当变分后验分布与真实后验分布之间的(Kullback-Leibler, KL)散度越大时,训练误差也越大。目前,单独使用VAE重构多孔材料结构模型的方法已经逐渐被GAN重构方法所替代。

GAN于2014年被提出,其在训练和生成样本的过程中不需要马尔可夫假设和对训练数据概率分布的先验推断,而是设计了两个模型(生成器G和鉴别器D)进行对抗训练[47]。RADFORD等[48]将原始GAN模型中的全连接神经网络替换为卷积神经网络(Convolutional Neural Networks, CNN)后形成的深度卷积生成对抗神经网络(Deep Convolutional Generative Adversarial Networks, DCGAN)能够更好地处理图像。MOSSER等[42]首次将DCGAN应用于多孔材料重构中,实现了三类岩石样本(Bead pack、Berea和Ketton)的重构,并通过评估两点相关函数、图像形态学特征以及单向有效渗透率来验证DCGAN重构模型与真实多孔材料的统计和物理参数匹配性。DCGAN重构流程如图1所示[42],首先把5003体素结构模型划分为多个643体素结构模型后构造训练数据集;生成器接收高斯分布的潜向量后通过反卷积等上采样操作合成假的结构模型;鉴别器的作用确定结构模型来自真实训练集还是假的合成结构模型。通过生成器和鉴别器的对抗训练直至鉴别器无法分辨结构模型的真假后即可使用生成器实现结构模型的快速重构。

图1 多孔材料DCGAN重构

与其他数值重构方法相比,DCGAN可以更准确地捕获微观结构特征并且能够在短时间内实现多孔结构模型的重构,其所用神经网络的全卷积特性允许生成大样本的同时保持计算效率。

KENCH等[49]提出一种名为sliceGAN的框架,实现了2D训练图片至3D模型生成的维度扩展,主要创新是将从2D训练图像中采样得到的真实图像和生成器生成的3D模型在3个笛卡尔坐标方向逐像素切片后得到的合成图像输入至2D鉴别器中训练鉴别器,该方法可以应用在各向同性和各项异性材料的重构中,sliceGAN训练过程如图2所示[49]。相对于DCGAN,sliceGAN不需要直接基于3D数据集进行训练,节约了计算资源和时间消耗。

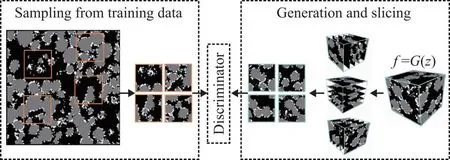
图2 sliceGAN训练过程

与DCGAN不同的是,MIRZA等[50]提出的条件生成对抗神经网络(Conditional Generative Adversarial Nets, CGAN),设计了接收用户自定义参数的接口,能重构出具有指定特征信息的结构模型。其将条件信息y作为额外的输入层分别输入至生成器和鉴别器中,以指导网络按照条件要求生成图像。CHEN等[51]提出另一种名为InfoGAN的条件控制生成网络,其将潜向量解耦为能控制图像生成的固定噪声和随机噪声,并且引入互信息概念约束固定噪声和生成图像。与CGAN网络相比,InfoGAN将固定噪声和生成图像的互信息加入至损失函数中,通过互信息的最大化实现固定噪声对生成图像更加有效的控制。

ZHENG等[52]提出一种名为条件ProGAN的生成对抗神经网络,融合了渐进增长生成对抗神经网络(Progressively growing GAN, ProGAN)架构[53]和CGAN架构并使用WGAN-GP损失函数以增加网络的训练稳定性。该网络最终可以根据用户定义生成指定孔隙率、材料类型以及两点相关函数的多孔材料结构模型,其网络架构如图3所示[52]。

图3 条件ProGAN网络架构

GAN自提出以来,其生成器都是以一个黑盒子的形式运行,人们缺乏对其图像生成特征控制机制的了解。KARRAS等[54]提出的StyleGAN重新设计了生成器网络架构,实现了在不同尺度上控制生成图像的特征,初步揭示了GAN生成图像的特征控制机制。该文的主要创新点包括:①借鉴风格迁移技术,提出了包括映射网络模块和合成网络模块的生成器网络,可无监督地分离高级属性和随机变异,实现了对生成图像中特定尺度属性的控制;②通过映射网络实现了对潜向量的解耦,避免了不同尺度上的控制向量发生纠缠;③提出了样式混合技巧,训练两个潜向量来生成图像,在图像合成时使两个潜变量随机切换以实现不同尺度样式的混合。FOKINA等[55]将StyleGAN应用在2D多孔材料结构重构任务中,确定StyleGAN相比于DCGAN具有更好的重构效果,并且重构出的样本具有与原始数据相似的概率分布。HUANG等[56]基于StyleGAN提出3DPmmGAN,用于3D多孔材料结构模型重构,可以定量控制所生成微观结构的形貌,并预测不同微观结构的统计特征。CAO等[57]将InfoGAN与StyleGAN相结合并且将孔隙率分布作为先验信息输入网络进行训练,以提高重构结果的保真度。

训练深度学习模型的必要条件是多孔材料结构模型大数据集的构建,基于生成对抗神经网络的多孔材料重构方法具有生成速度快、生成图像真实性好的优点,具有广阔的应用前景。本文以“生成对抗神经网络”和 “多孔材料”为关键词检索了Web of Science和中国知网数据库近三年基于GAN的多孔材料重构相关研究论文,并进行了总结,由表1所示。由表1可以看出,目前基于GAN的多孔材料重构目标主要集中在提高训练过程的稳定性及计算资源的节约、生成图像形态/特征信息的控制以及超分辨率等几个方面。

表1 基于GAN的多孔材料重构论文总结

1.3 多孔材料结构模型重构方法的评述

1.3.1 深度学习重构法的优势

实验重构法可以重构几乎所有的多孔材料,具有精度高、质量好等优点,但受到实验条件和成本限制,难以短时间内重构大批量图像;表征重构法具有算法简单、重构速度快等优点,但重构模型不能完全匹配真实材料;以GAN为代表的深度学习重构法结合了实验重构法和表征重构法的优点,其所使用的训练数据集是利用实验重构法构建的,能匹配真实的多孔材料。利用训练好的GAN模型可以在短时间内实现大量多孔结构模型的重构。

1.3.2 以目标为导向的模型重构方法

模型生成的目的是为了进行渗透率性能研究,本文基于模型生成方法本身的特点以及后续渗透率计算的要求,认为所设计的模型生成方法在满足真实性的要求后还应满足:

(1)面向多目标特征参数的条件化重构方法

前文所述的StyleGAN和CGAN等网络已经能够根据某些用户自定义的单个参数(如孔隙率、材料类型、两点相关函数等)而生成对应的3D多孔材料结构模型,但实际应用过程中也需要使用到其他的参数(如迂曲率,孔径分布、欧拉数等),因此,基于多目标特征参数的3D模型生成将是一个有意义的研究方向。

(2)面向流动性能研究的超分辨率重构方法

图像分辨率过低将导致多孔材料结构模型的相边界出现“锯齿”现象,影响LBM的计算精度。微米级的分辨率使得对流动性能有重要影响的亚微孔-喉结构无法显现。利用目前的微米级训练数据集,研究超分辨率重构方法,重构亚微结构模型将是另一个有趣的研究方向。在多孔材料重构领域,已有学者提出了一些超分辨率重构方法[59-63],但仍然需要更深入的研究以重构出高质量的亚微结构模型。

(3)面向流动性能研究的尺寸提升重构方法

大尺寸的多孔材料结构模型具有大的视界,更能保证LBM仿真结果的准确性,但由于计算资源的限制,训练GAN模型时不能使用太大尺寸的数据集,特别是针对3D模型,随着模型体素的增加,训练时计算资源的消耗也成倍增长。为此,研究小尺寸的训练集重构大尺寸的多孔材料结构模型也将具有重要的意义。

1.3.3 深度学习重构模型及训练方法的限制

以GAN为代表的深度学习重构模型已能够重构出接近真实的多孔材料结构模型,但是仍需要大量的计算资源和内存条件。昂贵的计算机硬件设备以及长时间的训练是限制学习重构模型应用的重要因素,所以需要发展更加高效的模型结构和训练方法。

深度学习模型在重构中的应用还受到数据集的限制,主要表现为两个方面:①现在尽管有一些多孔材料结构模型的公开图像数据样本,但仍不足以支持不同多孔材料结构模型重构方法的研究,因此需要制作更多种类多孔材料图像数据样本;②现在所制作的多孔材料结构模型样本太少,且尺度都比较小,不利于深度学习模型的训练,所以需要制作更多、更大尺度的原始数据样本或者在满足空间连通性的条件下发展合适的数据增强算法扩大训练数据集。

2 多孔材料渗透率预测方法

多孔材料渗透率预测主要利用经验关系式或深度学习方法,直接基于结构参数或图像进行快速预测。

2.1 渗透率计算的经验关系式

多孔材料孔隙图像中的渗透率与孔隙率、孔形、连通性、迂曲率等几何/形态特性具有直接的关系[64],相关学者研究建立了渗透率与多孔材料几何/形态特性参数之间的经验关系式。HOMMEL等[13]综述了常见的一些渗透率计算关系式。其中,应用最广泛的经验关系式为Kozeny-Carman方程和Ergun方程[65]。一些研究者也基于特定问题提出了不同的渗透率预测经验公式,如周期性圆柱阵列多孔材料[66]、致密砂岩储层[67]等。不过,渗透率计算经验关系式仍然有很大的局限性:

(1)缺乏针对不同种类多孔材料的通用模型,单个经验关系式基本上只能适用于一个或几个应用场景。

(2)目前大多数渗透率经验关系式引入的特征数量较少,所建立的经验公式泛化能力不强。

(3)经验公式一般只使用一阶统计量,在结构信息表征方面存在不足,难以引入高阶统计量。

2.2 深度学习渗透率预测方法

以2012年AlexNet网络的提出作为深度学习兴起的里程碑,本文总结了基于深度学习多孔材料渗透率方法的发展进程,如图4所示。图中时间轴表示常用深度学习模型的提出时间以及首次用于构建渗透率预测模型的时间。本文以“深度学习”和“渗透率预测”为关键词检索了Web of Science和中国知网数据库近五年的相关研究论文,将多孔材料的深度学习预测方法主要分为3类:①基于多孔材料结构参数建立的结构参数-渗透率回归预测模型,该方法首先需要人工提取多孔材料的结构参数,接着进行大数据集训练,从而建立结构参数与渗透率之间的关系模型;②基于数字图像建立的图像-渗透率回归预测模型,该方法直接建立图像与渗透率之间的关系;③基于深度学习的图像-流场-渗透率快速预测模型,其利用深度学习技术进行多孔材料的快速流场仿真,得到压降和流场平均流速后通过达西定律预测出渗透率。下文将对这些方法进行详细的阐述。

图4 基于深度学习的多孔材料渗透率方法发展进程

2.2.1 结构参数-渗透率回归预测模型

基于结构参数的渗透率回归预测建模流程如图5所示。首先,通过PNM等方法提取出多孔材料的结构参数(如孔隙率、迂曲率等);然后,通过LBM等流体仿真方法计算出结构模型对应的渗透率标签;最后,将结构参数和渗透率标签同步输入至DNN中进行训练后得到结构参数-渗透率回归预测模型。

图5 基于结构参数的渗透率回归预测建模流程图

DNN作为一种最常用的深度学习模型,具有非常强的非线性拟合能力,可被用于渗透率预测建模。其网络结构由输入层、隐藏层和输出层组成,如图6所示[68],输出层仅有一个神经元表示渗透率。

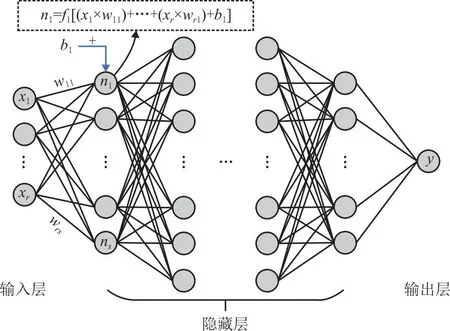
图6 DNN网络结构示意图

网络训练分为前馈过程和反向传播过程,数据集的特征参数经网络进行一系列线性和非线性运算后再通过输出层输出预测结果的过程即为前馈过程; 预测结果和训练标签之间的误差再通过网络进行反向链式求导后更新权重参数的过程则为反向传播过程。多次进行前馈过程和反向传播过程后直至误差收敛则表示网络训练完成。

闵可夫斯基形态学函数(Minkowski Functionals, MF)作为一种统计方法,常用于表征多孔材料。MF参数能很好地反映多孔材料的结构特性,有助于直接根据结构形态学特征预测渗透率,三维多孔结构的MF参数分别为体积、表面积、平均宽度和欧拉数。SRISUTTHIYAKORN等[69]提取多孔材料的MF参数至多层神经网络中建立了基于MF参数的渗透率回归预测模型。

神经网络算法训练过程的核心步骤是寻找损失函数的全局最优解,而选择的超参数合理与否会很大程度上影响训练过程的收敛速度和训练结果的精度。因此国内外一些研究者提出了一些结合机器学习算法和智能优化算法的渗透率混合预测模型,通过智能优化算法搜索最优超参数,提高了训练模型的精度和速度[71]。

表2对近五年来的一些基于结构参数的渗透率预测模型研究论文进行了总结,第3列统计了其网络结构信息,数据集项括号内数字分别表示训练集个数、验证集个数和测试集个数之比;第5列中R2为决定系数,MAPE为平均百分比绝对误差,RMSE为均方根误差。总结发现,目前基于结构参数的渗透率预测模型所用的深度学习算法均是DNN,不同的是其隐藏层深度、所用训练数据集种类或数量等。另外,特征提取过程完全由人为确定,选择何种类型或数量的特征对模型的准确率具有重要影响。

表2 基于结构参数的渗透率预测模型总结

2.2.2 图像-渗透率回归预测模型

结构参数-渗透率回归模型需要首先从图像中提取特征统计量作为深度学习模型的输入,提取特征的过程需要人工参与,容易丢失重要特征,因此一些学者开始设计特征提取网络自动提取多孔结构特征。CNN具有卷积层、池化层结构和端到端的训练方式,在图像处理方面具有天然的优势,常作为图像-渗透率回归预测模型中的特征提取网络。卷积层的主要作用是利用卷积核提取输入图像中的特征信息并形成特征图;池化层的主要作用是对特征图进行降维,增大后续特征的感受野,多次堆叠卷积层和池化层可以大幅度减少模型的训练参数。图7为典型特征提取网络结构,仅由堆叠了若干卷积层和池化层的一条支路组成,输入为图像,输出为展平的特征信息。

图7 典型特征提取网络

将特征提取网络提取的特征信息再输入至全连接神经网络中进行训练即可得到图像-渗透率回归预测模型,该模型的核心部分即为特征提取网络结构的设计,训练流程如图8所示。

图8 基于图像的渗透率回归预测建模流程图

SRISUTTHIYAKORN等[69]开始使用CNN直接基于二维/三维岩石图像预测对应渗透率。其首先制作了若干二值图像,使用LBM方法计算渗透率,构造出可用于监督学习的带标签数据集;然后将图像输入至典型特征提取网络和全连接神经网络的组合网络中进行训练,建立了基于图像的渗透率回归预测模型,表明该方法在渗透率预测建模领域的应用前景。后续有大量的研究者基于典型特征提取网络对不同多孔材料结构模型进行了渗透率预测建模研究。

网络堆叠的层数越多,则非线性表征能力越强,但是往往会出现梯度消失现象,从而导致训练困难,HE等[76]提出了ResNet框架,在VGG网络上增加残差连接模块,解决了该问题,大大提高了模型的训练速度。ALQAHTANI等[77]将其应用在三维多孔材料渗透率预测建模,结果证明了该网络十分适用于描述体积图像,而不需要特别复杂的模型调整。

上述深度学习模型均属于数据驱动类型,主要从数据中学习规律。为了得到高精度的训练模型,数据驱动的研究方法极其依赖于高质量的大型数据集,但受限于时间和实验条件,获取大量的样本的成本很高,而样本少又很容易导致训练的模型欠拟合。为减少对数据的依赖,一些研究人员尝试将物理方程等信息合并到深度学习方法中,形成了物理信息约束的深度学习方法[78-79]。在使用深度学习构建多孔材料渗透率预测模型的构建中,引入物理信息的常用方式是在模型架构中嵌入[80-81]。WU等[80]对常规的CNN渗透率预测网络进行物理信息扩展,在全连接层设计了两个单独的神经元分别接收孔隙率和比表面积参数,在预测二维Voronoi多孔结构时得到了与LBM仿真结果接近的预测效果。其网络架构以及预测结果如图9所示[80]。

图9 基于物理信息的CNN架构及渗透率预测结果

不同于在全连接层增加物理信息输入,TANG等[81]提出一种带有物理信息的深度学习模型预测渗透率,该模型引入了DenseBlock模块[82],并在每个DenseBlock模块前增加物理信息孔隙率和迂曲率。研究结果表明,该模型在小数据集上相比于KC方程、CNN模型具有更好的预测效果,其模型架构及预测结果如图10所示[81]。

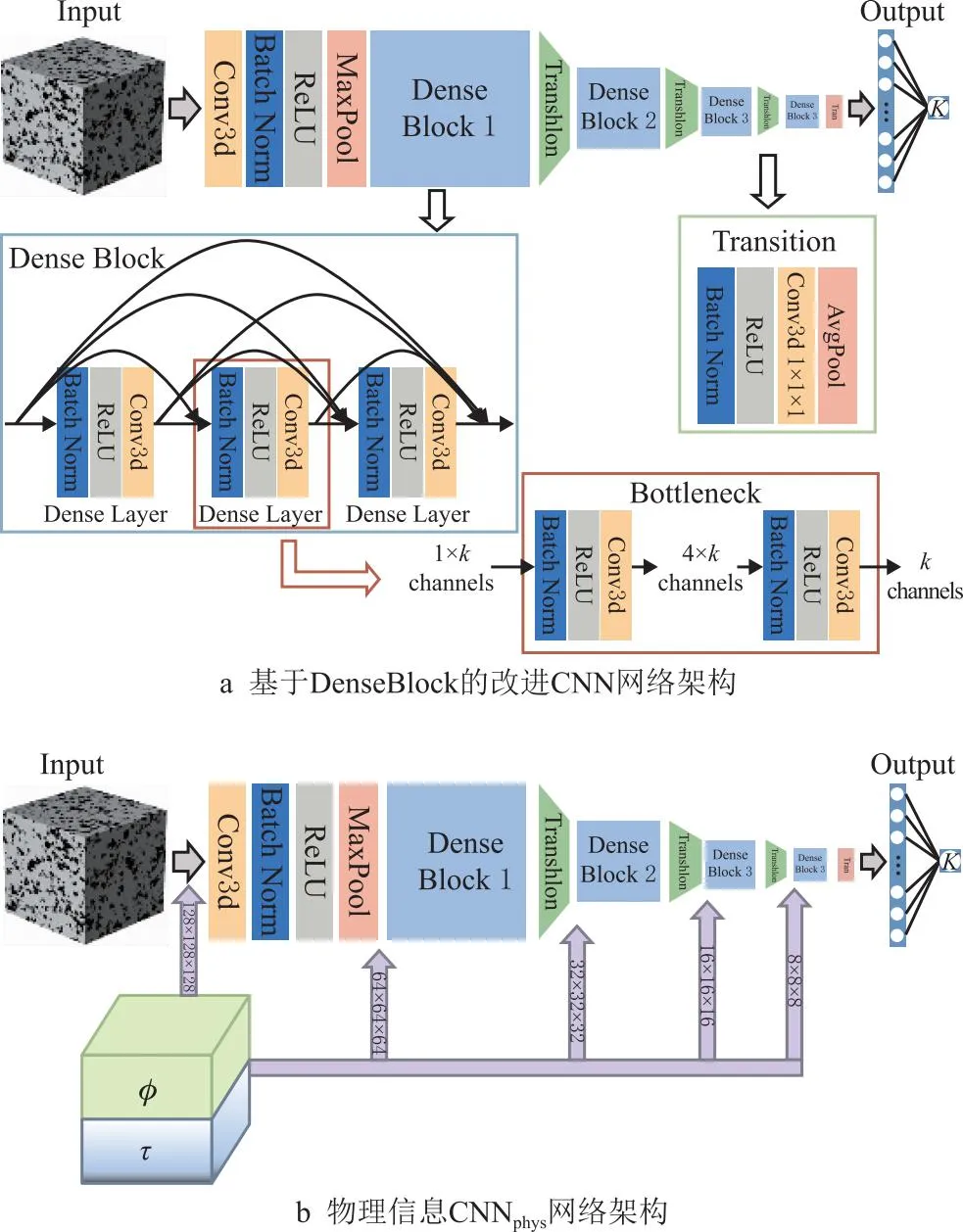
图10 基于Dense Block的物理信息CUN网络架构及渗透率预测结果

上述模型预测的结果均是单个渗透率值而不考虑其不确定性,BOM等[83]使用贝叶斯深度学习思想对渗透率和孔隙率的概率密度函数进行了预测建模。网络结构如图11所示[83],首先将图像经过编码网络编码为384维特征向量,然后分别训练多个回归网络建立渗透率、孔隙率和特征向量之间的关系,训练过程中采用蒙特卡洛dropout方法以一个给定概率随机抑制回归网络中的神经元,保证结果的不确定性,最后经过统计渗透率和孔隙率的频次构建出概率密度函数。

图11 不确定性建模网络结构

基于图像的渗透率预测模型实现了自动特征提取和端到端的训练方式。模型的预测性能与输入特征的选择没有相关性,而更多取决于模型架构和数据集。表3对近年来的一些基于图像的渗透率预测模型研究论文进行了总结,表中第3列网络结构中:Conv表示卷积层,Pooling表示池化层,Dense表示全连接网络的隐藏层,前面的数字表示网络层数。通过总结发现,目前,大多数研究工作的输入图像是使用实验重构法和表征重构法生成的,而学者们的研究重点是不同深度学习模型和不同种类数据集的应用。

表3 基于图像的渗透率预测模型总结

2.2.3 图像-流场-渗透率快速预测模型

近年来,大量学者开始使用深度学习技术构建各种几何结构(如圆柱、机翼等)的稳态流场预测模型,并表明该模型的求解时间远小于传统的CFD求解器[94-96]。该方法也被用于快速预测多孔材料渗透率,首先直接构建基于深度学习的孔隙尺度快速流场仿真模型,建立流场和图像之间的关系,然后通过式(1)[97]所示的达西定律即可计算出渗透率值。快速流场仿真模型主要包括推进模拟法[98]和稳态流场直接训练法[99-103],前者目的是在模拟中获取任意点的流场,后者直接输入图像进行稳态流场的预测[104]。

(1)

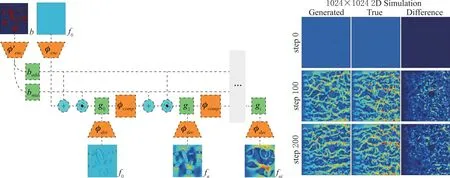
图12 Lat-Net网络架构以及仿真结果

gt=(gt⊙bmul)+badd。

(2)

因为深度学习快速流场仿真模型的输入和输出为同尺度的图像,所以具有编码-解码结构U-Net架构[105]及深度残差U-Net(ResUnet)架构[106]作为基础网络被广泛地应用于构建快速流场仿真模型并直接预测多孔材料的稳态流场。SANTOS等[99]提出的一种名为Poreflow-Net的改进ResUnet网络架构,能够根据输入图片预测稳态速度场。该网络包括4个编码分支和1个解码分支,编码分支用于接收预先提取的四类形态学特征,解码分支还原得到沿压力梯度方向的速度场预测图像。研究结果显示深度学习预测与仿真结果吻合较好,特别是对蓖麻砂岩(Castlegate sandstone)的渗透率计算结果与真实值之间的平均相对误差为1.06%,如图13所示[99]。

图13 Poreflow-Net流程及仿真结果

此外,WANG等[101]提出了使用基于PixelCNN++的门控U-Net架构预测和加速多孔材料的稳态流场仿真ML-LBM方法,能够预测3D模型的3个方向的速度场。以R2为评价标准,该模型预测2D和3D图像渗透率的精度分别达到0.99和0.97以上。

AKBIRI等[100]设计了一种U-ResNet架构进行二维多孔材料的快速仿真,该网络融合了U-Net和ResNet结构,如图14[100]所示。网络的输入为二维多孔材料图像,输出为速度场云图,训练图像的速度场云图采用LBM方法计算得到。该模型预测的x和y方向的渗透率值与真实值之间的皮尔逊相关系数(Pearson Correlation Coefficient, PCC)分别为0.986和0.949,均方根误差分别为0.019和0.026。TAKBIRI等[102]后续又改进了上述架构,所训练的仿真模型能够接收可变尺寸/大小的二维多孔图像。

图14 U-ResNet网络架构

CNN的训练过程是在空间域中进行,而傅里叶卷积神经网络(Fourier Convolutional Neural Network, FCNN)[107]则在频率域中进行训练。NIEKAMP等[103]将FCNN引入至2D多孔材料流场仿真研究中,其网络结构如图15所示,其中F为积分变换,F-1为逆变换,R为低通滤波,该网络结构主要在傅里叶神经算子层(Fourier Neural Operator,FNO)中设计了CNN和傅里叶变换两个并列层,同时进行空间域和频率域的计算,其中积分变换F分别验证了离散傅里叶变换(Discrete Fourier Transform,DFT)和离散余弦变换(Discrete Cosine Transform,DCT),以PCC作为评价指标,采用DFT的模型得到的效果更好,在x和y方向分别为0.983和0.938。

图15 FCNN网络结构

2.3 深度学习渗透率预测模型的评述

2.3.1 深度学习预测模型的研究现状

近年来,大量学者使用深度学习技术基于图像或基于结构参数构建了渗透率预测模型。另外,也有一些学者致力于使用深度学习方法进行多孔材料流场仿真,而后根据达西定律计算渗透率,但是该方法难以实现逐像素/体素匹配,仍然需要大量的研究[104]。

本文对近年的一些基于深度学习的多孔材料渗透率预测建模文献所涉及的结构模型生成方法和渗透率预测建模方法及其目标进行了分析整理,得到:①目前,构建结构参数-渗透率预测模型时使用的均是DNN算法,构建图像-渗透率回归预测模型时大多使用CNN算法,构建图像-流场-渗透率快速预测模型时大多使用U-Net网络作为基础架构;②现已构建的3种渗透率预测模型预测精度均优于KC方程等经验关系式。特别是使用多物理描述符、高阶统计量或多种类多孔结构模型进行训练后建立的渗透率预测模型更为准确,相较于经验关系式,通用性更好。

2.3.2 深度学习预测模型的研究展望

(1)深度学习与物理规律融合

深度学习模型的训练数据本身可能存在误差,数据集较少时,该误差的存在将会导致模型的不确定性因素增加。受限于实验条件,往往无法制作出多孔材料的大型数据集,将会对模型的泛化能力产生不利影响。一个有效的方案是使用物理信息降低数据误差对结果的影响,从而可以使小数据集也表现出较好的效果。因此,探索深度学习和物理规律相融合的耦合模型是该领域一个有价值的研究方向。

(2)深度学习评估经验关系式参数的有效性

由于孔隙率等物理描述符可以清晰地表示出多孔材料的结构信息,渗透率预测的经验关系式对研究复杂多孔材料性能具有重要意义。现在有很多经验关系式使用了不同的结构参数,评估所选物理描述符的有效性成为一个重要的问题。由于训练很好的深度神经网络可以提取出图像中蕴含的大量特征,且高阶统计量相比于一阶统计量可表征更丰富的信息,本文认为一种可能的方式是设计出合理的评价指标。以图像-渗透率回归预测模型的结果或引入高阶统计量所建立的渗透率预测模型为标杆,分析确定不同结构参数对渗透率结果的贡献度,从而选择出最合适的结构参数。

(3)深度学习预测模型具有可迁移性

目前在各工程制造学科中,建立合理的加工-结构-性能(Processing-Structure-Property, PSP)关系以获得对多孔材料行为的深入理解已然成为一个研究热点。数据驱动的深度学习技术能够在建立PSP关系的过程中起到重要作用,其中关键的一步即是在设计优化步骤中对性能进行快速计算/预测。一些渗透率预测研究领域的深度学习模型亦可迁移至其他领域,如热扩散系数预测[108-109]以及力学弹性模量预测[110]等。

(4) 深度学习性能预测研究为工程制造系统设计提供新的思路

仿生学如今发展迅速,其目的是研究和模拟生物体的结构、功能、行为及其调控机制,为工程技术提供新的设计理念、工作原理和系统构成,受到了大量学者的关注[111-112]。研究基于深度学习的渗透率预测方法,探索自然界中随机多相材料的流动特性,并结合3D打印技术,制造出性能优异的功能多孔材料,为多孔材料工程制造系统提供新的设计思路。

4 结束语

渗透率作为多孔材料的一种重要特性,用来描述多孔材料的流动能力。本文介绍了基于深度学习的多孔材料渗透率预测方法的3个步骤,重点总结了深度学习技术在多孔材料结构模型重构、渗透率预测方法中的最新研究进展并论述了该领域的发展趋势,主要结论如下:

(1) 高质量多孔材料结构模型的生成是深度学习快速预测建模的先决条件。以单元建模法、三周期最小曲面建模法为代表的正向建模法很难构建起适用的大型数据集。表征重构方法由于灵活性低且与真实图形的匹配性相对较差而逐渐被以GAN为代表的深度学习重构法所替代。基于StyleGAN和CGAN的深度学习重构网络已经在定制化重构方面有了一些成果,吸引了大量的学者投入其中,不过多目标控制的定制化结构模型重构方法仍然需要研究。另外,为满足LBM仿真及后续预测模型的要求,模型的超分辨率重构和尺寸提升重构也具有很大的研究价值。

(2)大量研究者基于深度学习技术建立了渗透率预测模型,主要包括结构参数-渗透率和图像-渗透率回归预测模型,两者均表现出了较高的预测精度。另外,也有一些研究者利用深度学习技术直接构建的图像-流场-渗透率快速预测模型来预测渗透率,不过该方法的流场仿真结果在高涡量和高流速区域存在较大误差,直接影响渗透率计算的准确性。

(3) 基于深度学习等方法构建的渗透率预测模型的精度均优于传统经验关系式,并且在通用性方面也表现出较强的优势,具有广阔的应用前景。另外,渗透率预测的深度学习模型也具有较强的可迁移性,有望应用于多孔材料传热性能预测等相关研究领域。

综上所述,利用深度学习技术建立多孔材料的渗透率预测模型由于其灵活性及快速性等优点已表现出广阔的应用前景,能够帮助人们更加深入地理解多孔材料结构对性能的影响,助力相关工程制造系统的研究与应用。不过仍需更加深入的研究,进一步提高所建立模型的准确性与可靠性。