基于RRT*-DR算法的机械臂避障路径规划
2024-04-10商德勇汪俊杰索双富
商德勇 ,汪俊杰 ,樊 虎 ,索双富
(1. 中国矿业大学(北京) 机电与信息工程学院,北京 100083;2. 中国矿业大学(北京) 智慧矿山与机器人研究院,北京 100083;3. 煤矿智能化与机器人创新应用应急管理部重点实验室,北京 100083;4.清华大学 机械工程系,北京 100081)
0 引言
机器人广泛应用于汽车、航空、物流、智能制造等各种行业。机械臂执行任务时,其快速合理的路径规划是高效完成任务的关键,其路径规划问题是国内外学者研究的重点方向之一[1]。机械臂的路径规划目的是给定一个目标构型,在满足机器人的运动学约束的前提下,求取一条从起始构型状态开始连接到目标构型并避开障碍物的可行路径,通常还要考虑实时性要求[2-4]。
对于移动机器人,常用的路径规划算法有基于图搜索方法的Dijkstra、A*[5-7],或是人工势场法[8-9]。串联机械臂机器人的空间状态由各个关节角确定,构型空间是六维空间。在这种高维空间中,A*等算法会出现“指数爆炸”的情况,计算量剧增[10],且需要对构型空间显式精确建模。研究显示基于采样的算法更加适合于高维构型空间[11]。其思想是在机器人构型空间内不断地随机采样,利用无障碍空间中的采样点构成连接起始点和目标点的路径。
LAVALLE[12]提出了快速搜索随机树算法(Rapidly-exploring Random Tree,RRT),但基本RRT算法由于采用均匀随机采样,其收敛速度慢、路径非最优、多次规划路径不一致,许多学者对其进行了改进。KUFFNER等[13]提出改进的RRT-connect算法加快了收敛速度。KARAMAN等[14]提出RRT*算法得到起点到终点的渐近最优路径。LSLAM等[15]针对RRT*收敛慢的缺点,提出智能RRT*算法(RRT*-smart),快速降低整体路径长度。NOREEN等[16]详细比较了RRT、RRT*和RRT*-smart,指出较长的计算时间在高维空间下会有更明显表现。马冀桐等[17]采用降维映射的方式将封闭形障碍在机械臂构型空间预先离线表示。GAMMELL等[18]改变了RRT*在空间中盲目采样的形式,被称为informed-RRT*,但是这种方法在起点、终点距离较大时不具有优越性。张振等[19]将采样点限制在以目标点为圆心的圆形区域内,且半径随节点碰撞情况动态变化,减少搜索盲目性。张立彬等[20]以栅格地图形式优化数据存储结构,查找相邻节点,提升了计算速度。
本文提出一种改进的动态区域采样(RRT*-Dynamic Region,RRT*-DR)路径规划算法,通过限制一个采样区域,减少不必要的路径扩展。采样区域随路径的优化而动态变化,快速获得一条最优避障路径。同时提出一种近障碍节点变步长机制,减少了碰撞检测失败次数,降低了计算量,提高了路径规划效率。
1 基于改进RRT*算法(RRT*-DR)的运动规划
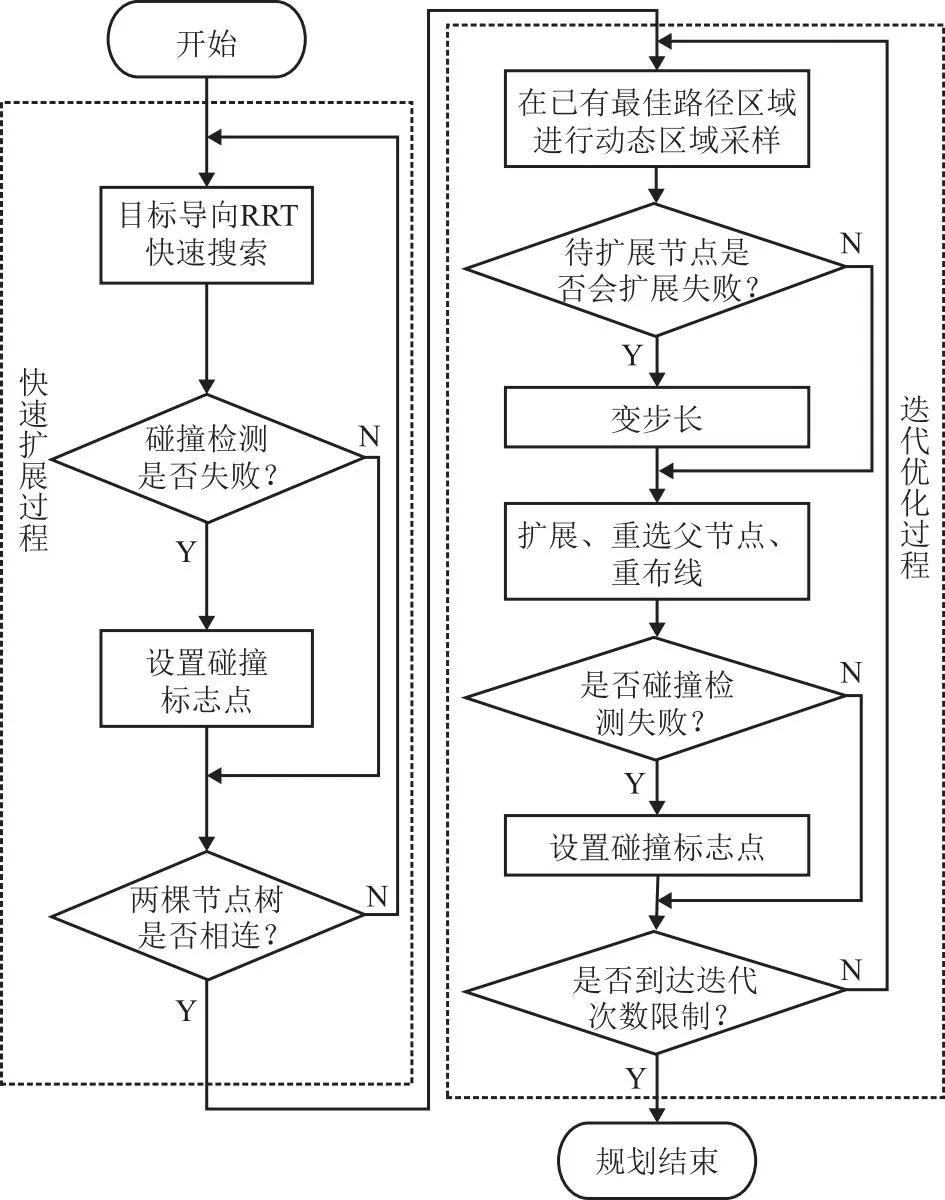
针对RRT*收敛速度慢的问题,提出一种改进的路径规划算法RRT*-DR。核心思想是将规划过程分为扩展和优化两个步骤,首先利用半目标导向的RRT快速搜索到一条初始路径,之后利用动态区域采样的RRT*对该初始路径进行迭代优化,使其快速收敛到最优路径。
1.1 基本RRT与RRT*算法原理
RRT算法是针对高维空间路径规划问题最常用的算法之一,其基本原理是在构型空间随机采样一个节点,在已有节点树中找到距该随机点最近的节点,朝随机点扩展一个步长得到一个扩展点,若扩展途中没有障碍,则添加该扩展点和扩展路径到节点树上[21]。通过不断重复上述步骤,即可扩展出一棵节点树,探索整个空间。RRT算法的缺点是无法得到最优路径,路径代价较大,这一问题在RRT*上得到了解决。
RRT*算法在经典RRT的基础上,增加了重选父节点和重布线过程。经由每一步扩展之后的重选父节点和重布线的处理,节点趋向于连接邻域内路径代价最小的点,随着迭代的进行,所有节点都趋近于以最小路径代价连接到起点,节点树趋于平滑。起点到无障碍空间任一点都是在保证避障的前提下,通过相对最短的接近直线的路径来连接。同理,经过足够迭代,也能保证起始点到目标点的路径渐进最优性。
1.2 半目标导向的快速扩展过程
传统算法的随机树采样过程采用均匀采样,尽可能地探索到整个空间,具备很强的探索性,但忽略了目的性,即朝向目标运动的最终目标。若过于强调探索性,对整个空间的探索会浪费大量时间和资源;若过于强调目的性,会因为障碍物的拦阻而受困于局部极小值。因此,需要平衡扩展的探索性和目的性。对此,采用半目标导向的扩展方式,如图1所示,设置一个目标导向阈值p,在每次采样之前取一个随机数rgoal,并与p比较。若rgoal

图1 半目标导向
该扩展方式可以兼顾探索性和目的性。一方面,将目标点作为随机采样点时可以使节点树快速接近目标;另一方面,随机得到采样点可以向自由无障碍空间扩展,绕过障碍,避免陷入局部极小。当环境中障碍物比较多时,可以适当增大p以提高随机探索概率;当障碍物比较少时,可以适当减小p以增大目标导向的概率。
半目标导向采样函数的伪代码如表1所示。

表1 半目标导向采样
1.3 动态采样区域优化过程
找到初始路径后,进入优化过程。传统RRT*的优化过程针对整个空间进行扩展优化,导致其在高维构型空间收敛缓慢[22]。
本文对RRT*算法进行改进,引入动态区域优化方法,用于优化初始路径。其思想是在初始路径节点构成的初始路径周围进行采样扩展,且随着RRT*的优化,初始路径逐渐改变,采样范围也随之改变,即始终在当前最优路径周围进行采样扩展和优化,如图2所示。

图2 动态区域优化原理图
将扩展资源全部用于对改善路径有帮助的区域,且在有限区域内可以快速增大节点密度,密化节点树,进而快速得到渐进最优的路径。动态区域优化过程伪代码如表2所示。

表2 动态区域采样
在路径节点周围一定范围内采样,只密化有意义区域的随机树,而放弃远离起点终点的区域。每次得到新的树节点后,进行的重选父节点和重布线过程可以优化随机树,得到长度更短的新路径。如此循环迭代得到一系列新的路径节点,可以在新路径节点周围采样,经过持续迭代,可以快速收敛到最优路径。在优化路径过程中,重选父节点和重布线过程的选取范围为一个圆,其半径为rneighbor,该值影响算法执行时间。随着迭代的进行,树节点密度增大,若rneighbor始终保持在较大数值,在每次重选父节点、重布线过程中会涉及大量近邻节点的计算,将消耗大量计算时间。因此,随着迭代次数的增加,应逐渐减小rneighbor,并最终收敛到一个定值,如式(1)所示:
(1)
其中n为节点树上的节点个数。由式(1)可知,当节点树开始扩展时,rneighbor大小为其初始值。随着节点树扩大密化,节点增多,rneighbor逐渐减小,最终收敛到初始值的0.2倍。
1.4 近障碍节点变步长机制
RRT及其扩展算法都属于单线查询型算法[23],因其基于采样的特性,可以不对障碍物进行显示建模,故提高了环境适应性。对于环境障碍物的探索,通过碰撞检测环节完成,而碰撞检测环节是整个扩展寻路过程中最耗时的环节,在障碍物集中的区域尤其严重,且因为碰撞检测失败而舍弃的节点也占到了总迭代节点数量的一半以上[24]。传统RRT*在扩展得到新节点之后进行碰撞检测,碰撞检测失败的节点被直接舍弃,没有得到利用,不能为后续扩展提供指导。本文提出一种近障碍节点变步长机制,即将每一次碰撞检测失败的节点单独放置,进行记录,后续将树节点向随机点扩展时,先判断该随机点是否邻近障碍物,若随机点临近障碍物且待扩展树节点距离随机点较近时,缩短扩展步长,使扩展得到的新节点靠近障碍而不碰撞,如图3所示。既避免了碰撞检测失败舍弃节点而浪费扩展时间,又使得随机树更加靠近障碍,进而使得规划路径更优。
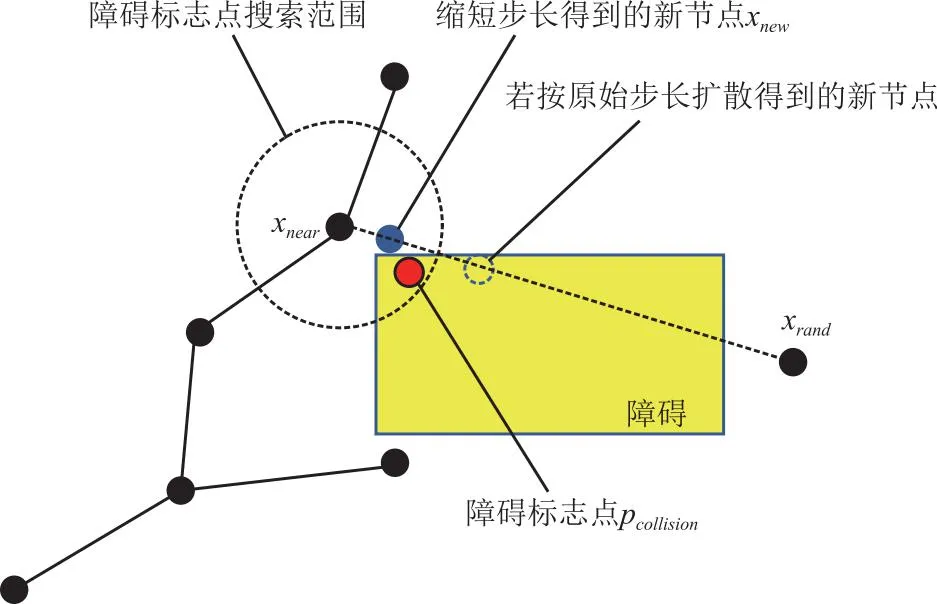
图3 近障碍节点变步长机制
RRT*的碰撞检测过程将算法扩展步骤得到的连接树节点和随机采样点的路径连线平均分为若干段,判断每一均分点是否使障碍相撞。若其中至少有一个均分点与障碍相撞,则检测失败。将碰撞检测失败的路径均分点命名为障碍标志点pcollision。当采样得到随机点后,进行扩展步骤,搜索到随机树中相距最近树节点,即待扩展点。随后判断待扩展点周围半径r的圆形范围内是否存在障碍标志点。若不存在,则表示待扩展点远离障碍,可按照原步长stepsize扩展;若存在,则表示待扩展点靠近障碍,有碰撞障碍的可能,得到待扩展点到最近障碍标志点间的距离l。
计算障碍标志点到待扩展点与随机采样点形成的直线的距离d,以此判断在扩展方向上是否存在障碍标志点,如式(2)所示:
(2)
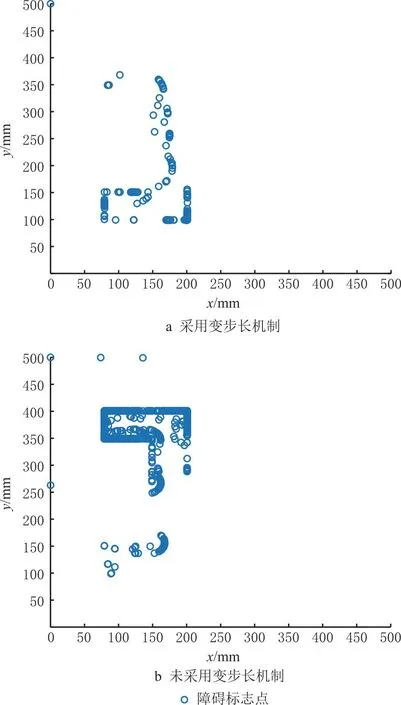
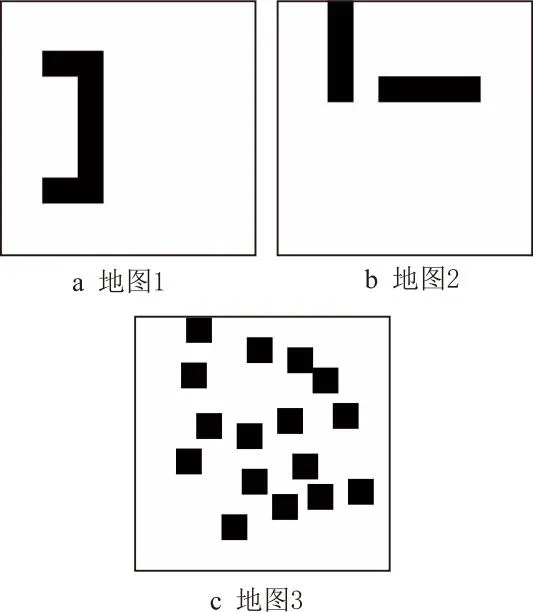
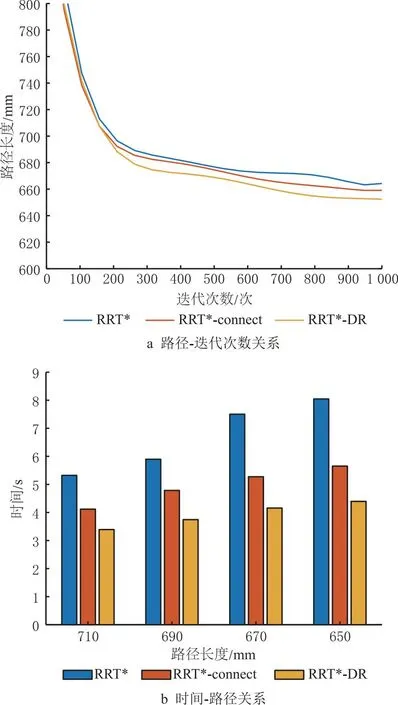
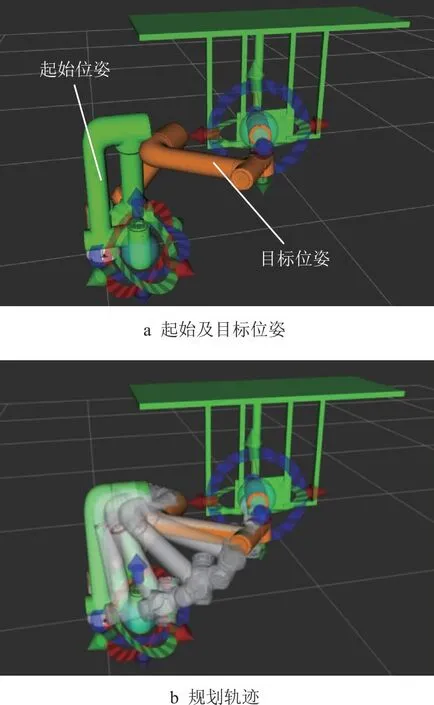
当待扩展点到最近障碍标志点的距离小于原始扩展步长时,若上述距离d小于设定阈值d0,则表示待扩展点的扩展方向上有障碍存在。在l小于步长且d (3) 近障碍节点变步长机制伪代码如表3所示。 表3 近障碍节点变步长机制 为验证近障碍节点变步长机制的有效性,在地图1中进行仿真实验。设置相同的输入参数与迭代次数,分别使用完整的RRT*-DR算法和未采用变步长机制的RRT*-DR,比较与障碍物碰撞的次数以及规划消耗时间。图4a和图4b分别是由未加变步长机制和采用变步长机制的RRT*-DR扩展过程得到的pcollision分布图。障碍标志点pcollision用圆圈表示,显然若圆圈越密集,则表示碰撞次数越多。由图4可见,采用变步长机制的扩展过程,蓝色圆圈更少,即其与障碍碰撞的次数更少。通过5组对比仿真得到结果如表4所示,未采用和采用该机制的算法平均碰撞次数分别为1416.2次和585.4次,可见采用该机制后碰撞次数减少58.7%,且规划时间相对减少24.3%。故采用近障碍节点变步长机制,通过减小靠近障碍标志点的节点的扩展步长,有效降低了与障碍物的碰撞次数,进而减少重新取点扩展的重复操作,有效缩短了规划时间。 表4 近障碍节点变步长机制比较 图4 有无近障碍节点变步长机制的规划仿真 为进一步提高搜索效率,引入RRT-connect算法的思想,使每次迭代产生的随机点xrand轮流作为起点节点树和终点节点树的引导点,并分别对起点节点树和终点节点树进行扩展,即同时从起始点和目标点生长出两棵节点树,并利用半目标导向机制的引导作用,着重朝另一节点树的方向扩展出新节点,加快对状态空间的探索和初始路径的产生。原理如图5所示。 图5 connect思想 connect思想执行步骤为: (1)执行半目标导向机制,得到一个随机点xrand,从起点节点树搜索欧式距离最近的树节点,并以其为基础扩展出一个新节点xnew_s,添加到起点节点树上; (2)同步骤(1),产生一个随机点xrand,从终点节点树搜索欧式距离最近的树节点,并以其为基础扩展出一个新节点xnew_e,添加到终点节点树上; (3)判断xnew_e的周边邻域内是否存在起点节点树的节点,若存在,则将xnew_e与其连接,得到初始路径;否则重复步骤(1)~步骤(3)。 connect思想伪代码如表5所示。 表5 connect思想 综上,RRT*-DR算法流程图如图6所示。 图6 RRT*-DR算法流程图 本章在MATLAB环境下仿真验证RRT*-DR算法的有效性与优越性,与RRT*、RRT*-connect算法比较。仿真设备平台的配置为主频2.30 GHz的Intel Core i5-6200U CPU,内存16 GB,搭载Windows 10和Ubuntu 18.04双操作系统。 在MATLAB中分别导入如图7所示3种500 mm×500 mm地图环境,分别对各算法的越障能力、寻优能力、复杂环境寻路能力进行验证。其中白色部分为自由空间,黑色部分为障碍空间。 图7 仿真地图 地图环境1中以(90,250)为起始点,以(400,250)为目标点,环境障碍在地图环境中呈对称结构,并半包围起始点,考察算法的越障能力。各算法的基本参数设置为相同,步长为20 mm,目标导向阈值p为0.5,迭代次数为800次。3种算法仿真结果如图8所示,分别进行20次重复测试,将测试指标整理数据如图9所示。 图8 地图1中的算法规划效果对比 图9 地图1中的仿真结果对比 由图9a可知,本文所提RRT*-DR算法在迭代次数较少时便可得到相对于RRT*与RRT*-connect算法路径代价更小的路径,平均比RRT*路径短,且随着迭代次数的增多,可以快速收敛到最佳路径。图9b中比较了两种算法在得到一定路径代价的路径所需要的规划时间。在该障碍情况较为简单的地图中,路径优化到接近最优路径时,三者所需时间较为接近,整体上看RRT*-DR得到较优路径所需时间更少,收敛速度相比RRT*更快。3种算法仿真结果数据对比如表6所示。 表6 地图1中的仿真数据对比 地图环境2在设置有直接分割起点终点障碍的基础上,增加一个障碍缺口,提供一个同伦类路径的选择。若连接起点终点的一条路径,在不分离和跨过障碍的基础上,能够连续变换为另一条路径,则这两条路径同伦[25]。增加不同同伦类路径通道,可以测试算法是否具有良好的优化能力,收敛得到一条代价最小的路径。分别以(5,5)为起始点,(300,140)为目标点进行路径规划,仿真结果及数据如图10和图11所示。 图10 地图2中的算法规划效果对比 图11 地图2中的仿真结果对比 RRT*与RRT*-connect在地图2环境中迭代次数较少时无法规划成功,迭代次数在500次以上才有较高的规划成功率,且经过迭代路径代价依旧较高,如图11a所示。而RRT*-DR以较少迭代次数就可收敛到最优路径长度。由图11b可看出,RRT*-DR将路径优化到一定长度所需规划时间小于RRT*。3种算法仿真结果数据对比如表7所示。 表7 地图2中的仿真数据对比 地图环境3设置有大量杂乱矩形障碍,模拟障碍物较多的复杂环境,考察各算法对多障碍环境的适应性。分别以(5,5)为起始点,(450,450)为目标点进行路径规划,得到的结果及仿真数据如图12和图13所示。 图12 地图3中的算法规划效果对比 图13 地图3中的仿真结果对比 由图13可知,在地图3环境中3种算法的优化收敛速度比较接近,但RRT*-DR算法所需要的规划时间较少,可有效减少碰撞次数,提高路径规划效率。3种算法仿真结果数据对比如表8所示。 表8 地图3中的仿真数据对比 通过平面地图仿真实验可验证RRT*-DR算法具有时间短、路径优的优势。相对于二维地图,三维地图环境中坐标点的描述多一个维度,本文所提出的RRT*-DR算法的核心是半目标导向机制、动态区域采样机制和近障碍节点变步长机制,均通过采样点的坐标统计和相关距离计算实现,在坐标增加一维时,其效果不受影响,故该算法可适用于三维地图环境。 在电脑主板研发阶段为验证设计合理性,需要对样板上各电子元器件的电学性能进行调试和测试,传统方式通常由人工手持示波器探针进行焊点检测。由于主板待测焊点尺寸小、密度大,准确地按压待测点有一定难度,且操作人员长时间工作容易产生视觉和肌肉疲劳,用机械臂夹持探针进行触点点测是一种低成本高效率的解决方法。 主板检测机器人是通过机械臂末端夹持探针来实现的,机器人检测实验平台如图14所示。主板夹具将主板竖直装夹在机架上,中央平台上放置示波器以及键盘等主板外设。布置两台机械臂于主板两侧,可同时实现两组测点的检测需求。 图14 主板检测实验台 主板检测环境存在着主板、夹具、机架等障碍物,属于多障碍物复杂环境,为检测带来较大困难,快速高效合理的路径规划是实现检测的关键。 为检验本文提出的RRT*-DR算法的有效性,使用法奥FR5协作机器人在主板检测环境中进行实验验证。首先在机械臂ROS系统进行可视化仿真,模拟主板检测的实际工况。借助ROSmoveit!的C++编程接口编写运动仿真程序,导入机器人的URDF模型,将RRT*-DR路径规划算法添加到运动规划库OMPL中,使用moveit!完成调用和规划。由rqt_graph得到各ROS节点框架关系图,如图15所示。运动仿真步骤为:机器人从初始蜷缩状态出发,点测主板正面测点。仿真环境中的运行结果如图16所示。机械臂从初始位姿以较短路径到达目标位姿,成功避开障碍。 图16 ROS机械臂运动仿真 在试验台法奥FR5机械臂控制系统中导入RRT*-DR算法进行实验验证。如图17所示,主板被固定在机架上,机械臂末端安装探针,从初始位置出发,执行路径规划得到的路径,最终避开障碍平稳准确到达待测焊点目标位置。进行20次路径规划算法测试,平均规划时间为2.416 s,且全部成功。验证了本文算法的实用性和有效性。 图17 机械臂运行实验 本文针对机械臂运动路径规划问题,提出一种基于RRT*的改进算法RRT*-DR。在传统RRT*的基础上,将整个规划过程分为快速扩展过程和优化过程,首先利用半目标导向的RRT快速扩展找到一条初始路径,随后利用动态区域采样对初始路径进行优化,快速收敛到渐进最优路径,避免了盲目探索与优化。此外,引入了近障碍节点变步长机制,进一步减少碰撞次数,节省了碰撞检测失败的时间和随机树节点消耗。在MATLAB中进行了3种不同地图环境下的仿真,通过比较多种算法的路径代价、迭代次数、时间、碰撞次数等评价指标,验证了本文所提算法的有效性和优越性。该算法用于电脑主板检测机器人路径规划,实现了机械臂安全高效避障,验证了该算法的有效性。在此研究基础上,未来可对进一步进行冲击最优优化,以减小机器人关节电机的冲击,提高机器人运动的平滑性。

1.5 connect思想


2 仿真验证
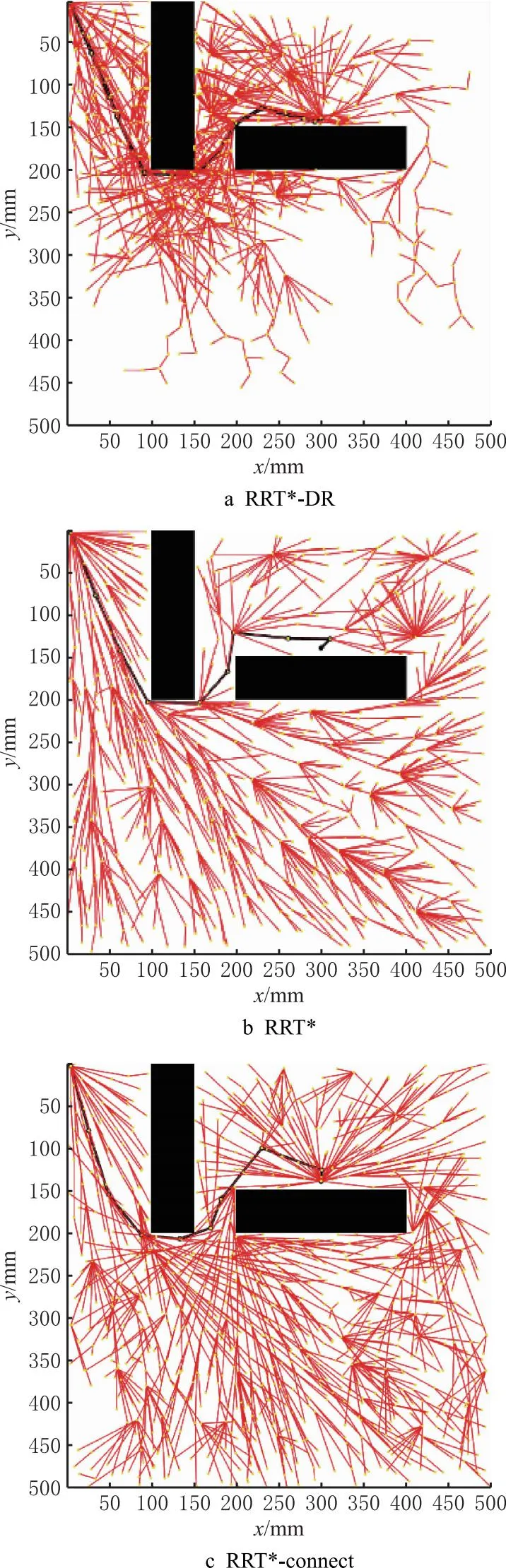
2.1 地图1

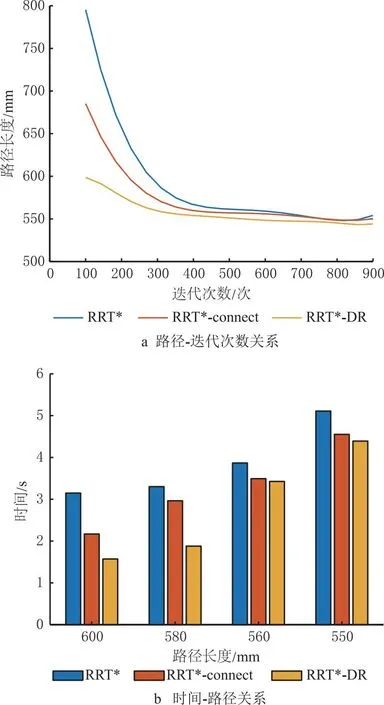

2.2 地图2
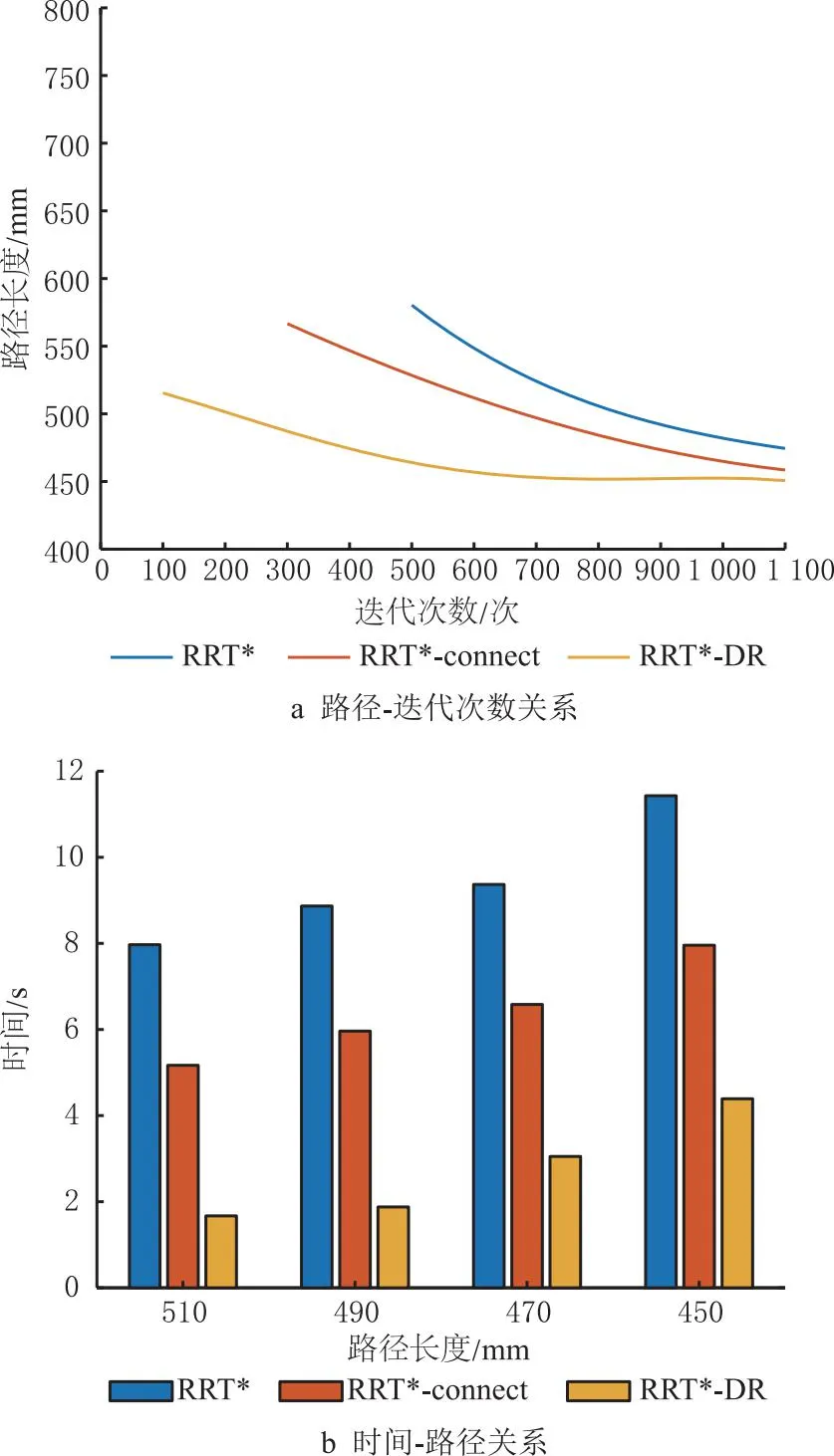

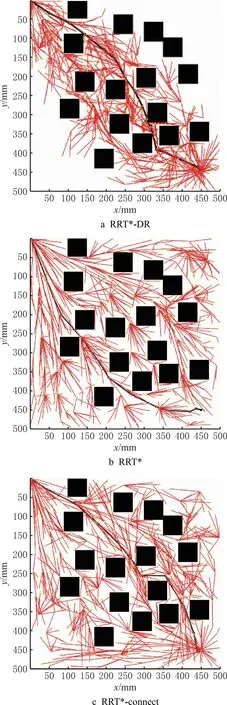
2.3 地图3

3 实验验证


4 结束语
