应力驱动的2.5D梯度各向异性维诺多孔零件轻量化建模方法
2024-04-10潘文珺江开勇
曹 伟,潘文珺,刘 斌,路 平,江开勇
(华侨大学 福建省特种能场制造重点实验室/厦门市数字化视觉测量重点实验室,福建 厦门 361021)
0 引言
随着碳达峰与碳中和等概念不断推广与实践,机械零件的轻量化问题逐渐成为我国现代制造业面临的新挑战,尤其是对于航空航天、汽车制造、生物医疗等高科技行业,在实现节约资源、能源和环境保护方面均起着举足轻重的作用。由于多孔结构具有轻量节材、比强度高、比表面积大、馈能减振等优点[1],使得多孔结构设计成为零件轻量化的关键。通过对多孔零件孔隙率、孔径大小及孔分布等参数的精准调控,可以在满足零件形状约束和力学性能约束的前提下减少材料消耗,实现轻量化[2]。
多孔零件的传统制造方法包括液体发泡、盐浸、冷冻干燥、选择性腐蚀、电沉积和气相沉积等[3-4],由于具有较强的随机性,缺乏对内部结构进行精准控制的能力,造成零件性能差异较大,且制造周期长,成本高[5]。近年来,随着增材制造技术的飞速发展,使得具有复杂内部结构的轻量化多孔零件的快速制造成为可能,因此,面向特定应用场景下多孔零件的建模方法及其性能控制逐渐成为当前增材制造技术最具挑战性的研究方向之一。
使用规则的晶格单元阵列式填充零件设计域是一种常见的多孔零件设计方法[6]。YAN等[7]采用蜂窝结构设计了一种增强型管状零件用于能量吸收优化研究,该结构相较于传统结构具有更高的弹性模量和峰值应力。LIU等[8]提出一种增强节点型体心立方晶格结构,能显著增强多孔零件的屈服应力、抗弯强度和能量吸收效果。FENG[9]等提出一种新型三周期极小曲面(Triple Period Minimal Surface,TPMS)晶格结构设计算法,该算法能在零件设计域内自适应阵列多种不同TPMS胞元,在保证几何连续性的同时还能减小应力集中、增大结构强度。虽然晶格结构设计过程简单、设计周期较短,适用于大多数简单零件的建模[10],但相对固定的胞元形状、简单的阵列规则也限制了其设计自由度,导致其可控性不高,难以对内部结构进行精准调控和自由设计,无法满足复杂零件在复杂工况条件下的轻量化设计需求。
与晶格结构相比,随机多孔结构具有更高的设计自由度,能够更容易地实现复杂零件的建模和性能控制。ULLAH等[11]采用分形几何的思想建立了全连通的随机多孔结构。YANG等[12]提出一种基于函数的随机多孔零件建模算法,能够通过控制孔的大小和分布生成非均匀的梯度多孔支架。曹伟等[1]提出了一种基于k-nearest算法的增强型正交各向异性多孔结构设计方法,能够实现对各向异性程度、方向和力学性能梯度的精确控制。DAYNES等[13]提出一种基于拓扑优化的功能梯度多孔结构建模方法,并通过实验证明在相同重量下其强度和刚度远高于体心立方晶格结构。此外,由于维诺多孔结构被认为是一种能够模拟自然界物体的理想结构,如骨骼、贝壳、竹子等[14],近年来对维诺多孔结构的研究逐渐成为热点[15- 16]。MARTíNEZ等[17]于2016年提出一种基于支杆的3D维诺多孔结构生成算法,通过调整设计参数可以在计算机上生成具有不同几何结构的多孔结构;随后,又提出了一种基于多边形维诺图的3D正交各向异性梯度多孔结构[18]。LIU等[2]提出了一种2.5D自适应重心维诺多孔零件建模方法,通过维诺站点分布控制孔隙分布,通过隐式曲面控制孔隙大小。
综上所述,虽然上述方法均能对多孔零件进行建模,实现零件的轻量化设计,但规则的晶格多孔零件建模方法设计自由度较低、控制困难;而由随机多孔结构建模方法生成的多孔零件,其内部力学性能梯度分布与零件的应力分布匹配困难,导致零件的力学性能下降。此外,部分建模方法采用的支杆结构在连接点处过渡不光滑,会产生应力集中现象,进一步降低了多孔零件的力学性能。因此,本文提出一种应力驱动的2.5D梯度各向异性维诺多孔零件轻量化设计方法,该方法能将零件内部的应力的大小映射为维诺站点分布,控制多孔零件的维诺胞元(孔腔)大小和分布,实现对多孔结构梯度力学性能的精准调控;将应力的方向映射为维诺胞元的朝向,实现对多孔结构各向异性的控制;此外,还通过调和距离场算法使支杆节点过渡光滑,减小应力集中现象,提高多孔零件的力学性能。
1 梯度各向异性维诺多孔零件建模
1.1 建模流程
应力驱动的梯度各向异性维诺多孔零件建模流程如图1所示。初始输入为2.5D零件的二维轮廓、蒙皮厚度μ及其受力F,其内部空间即为多孔结构设计域。根据零件受力状态对其进行有限元分析,可以得到零件设计域内的应力场。通过加权随机采样算法将应力场的大小(标量场)映射为设计域内的维诺站点分布,控制维诺胞元大小和位置,实现力学性能的梯度分布;将应力场的方向(矢量场)映射为二维黎曼流形,通过黎曼椭圆控制维诺胞元的各向异性。提出一种基于胞元择优生长策略的各向异性维诺图生成算法,生成胞元沿黎曼流场分布的各向异性维诺图。然后,将维诺图的边界偏置为厚度为τ的多孔结构内壁,并通过调和距离场算法对内壁节点处进行光滑处理,生成光滑的2D维诺多孔结构。最后,对2D维诺多孔结构进行拉伸,得到2.5D各向异性梯度维诺多孔零件。
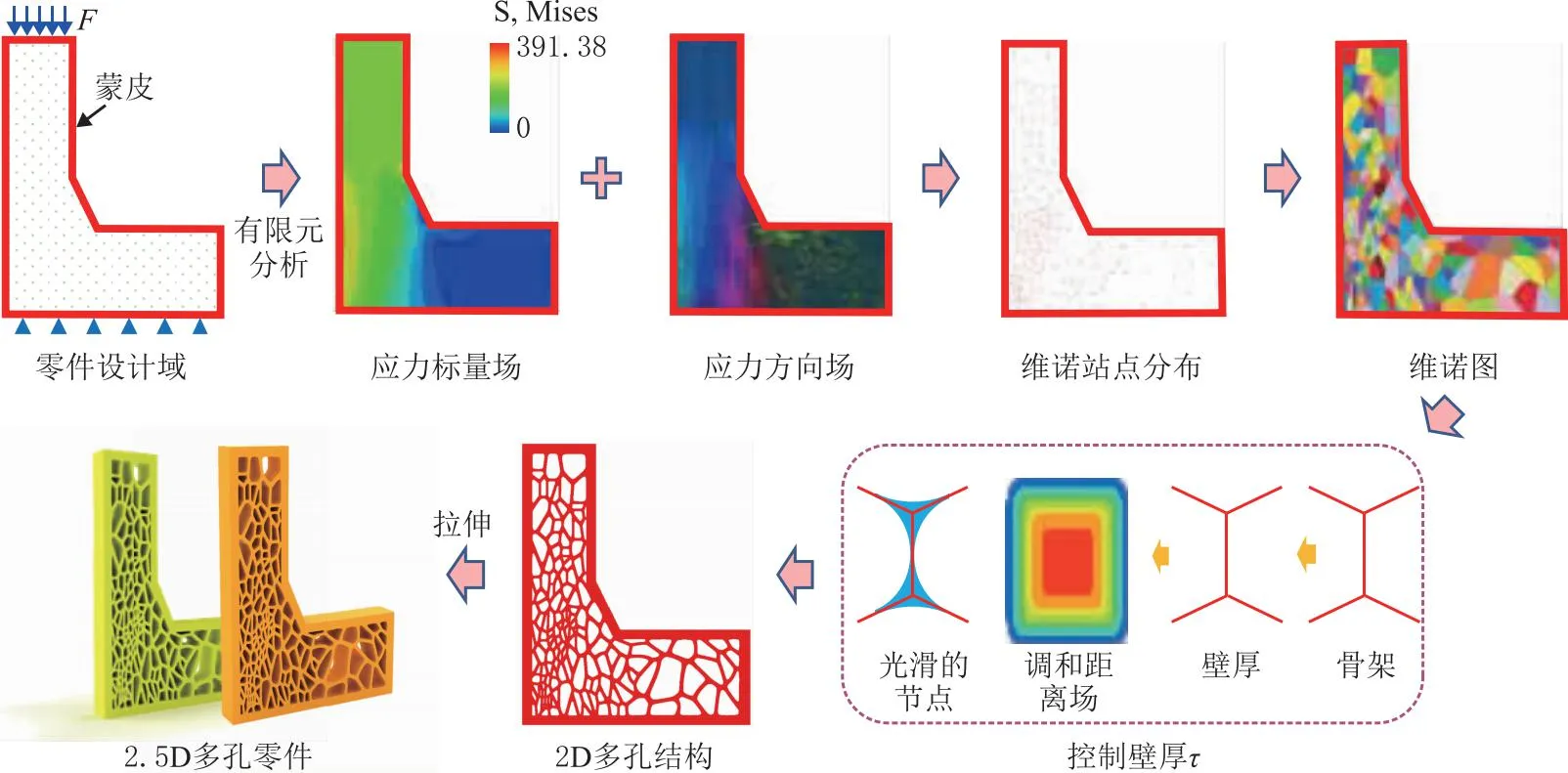
图1 应力驱动的各向异性梯度维诺多孔零件建模
1.2 应力场
本文通过应力场控制维诺多孔零件内部维诺胞元的大小、分布和各向异性朝向,实现材料、力学性能的梯度分布和各向异性,提升多孔零件的力学性能,降低材料消耗。通过有限元分析,可以获得零件在特定工况条件下的应力场。由于应力场是矢量场,可以将其分解为应力标量场σ(x,y)和应力方向场Θ(x,y),如图2所示。
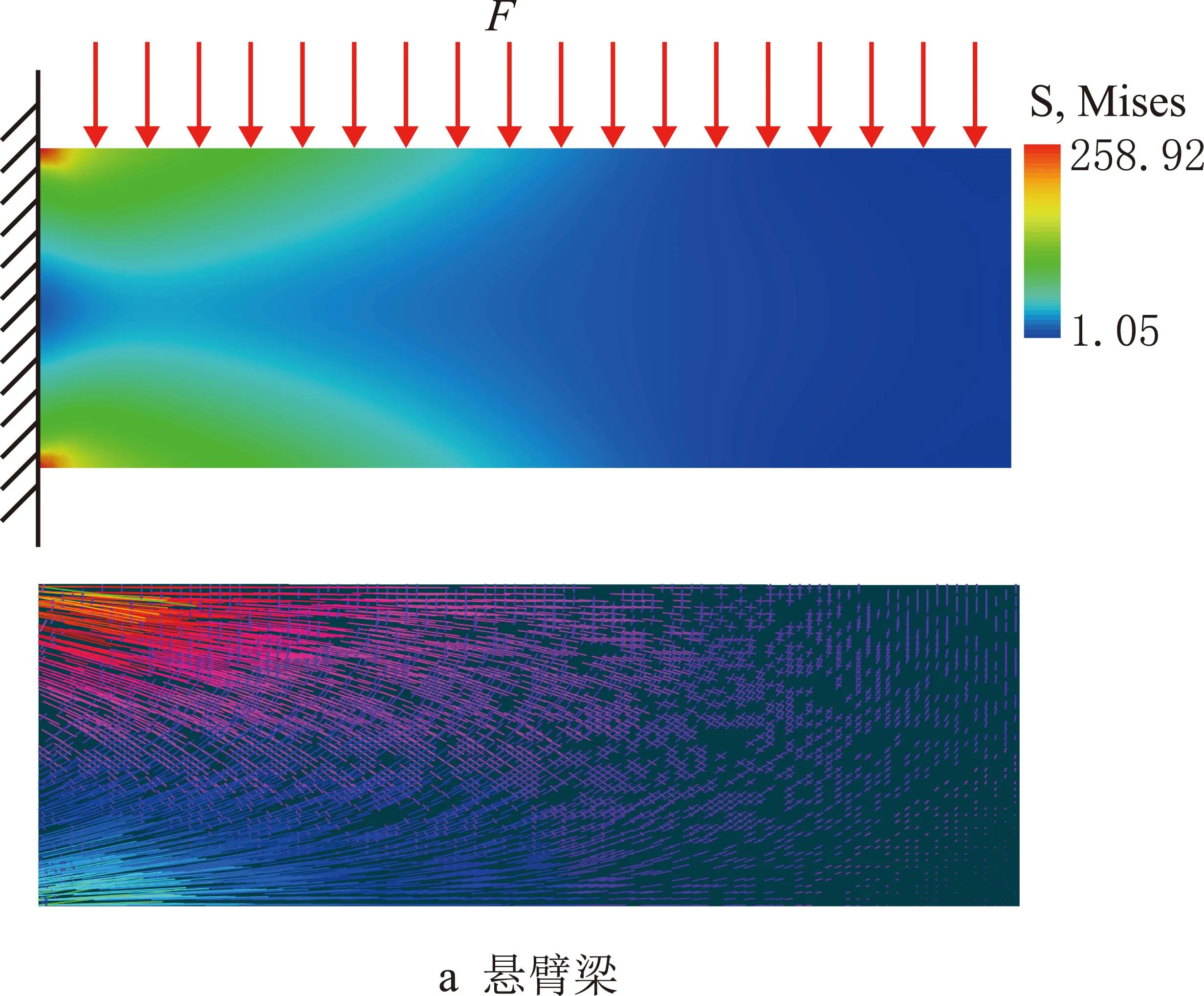
图2 零件的应力场
1.3 维诺站点加权随机采样
维诺站点的分布和多孔零件内维诺胞元的分布一一对应,即每个维诺站点对应一个维诺胞元。同时,维诺站点的分布特征由应力标量场σ(x,y)映射得到,是多孔零件实现材料和力学性能梯度分布的根本因素。其原因在于维诺站点的分布特征决定了多孔零件在3D打印过程中材料的局部分配规则,从而直接影响其局部力学性能。具体来说,应力大的区域分布的维诺站点数量多,维诺胞元密集,因而在零件打印时分配更多的材料以提高该区域的力学性能来抵抗弯曲、断裂等形变;相反地,应力较小区域分布的维诺站点少,维诺胞元稀疏,力学性能相对较低,材料分配少,以实现轻量化。
基于上述原则,本文提出一种加权随机采样算法将应力标量场σ(x,y)映射为维诺站点的分布。以正方形零件设计域为例,设需要采集的站点总数为N,算法步骤如下:
步骤1将零件设计域D作为四叉树数据结构的根节点。
步骤2将当前节点S对应的区域等分为4个栅格,即当前节点的子节点Si,i∈{1,2,3,4}。
步骤3按式(1)计算当前节点所对应区域的平均应力值δavg,按式(2)计算其子栅格的应力值δi:
(1)
(2)
步骤4对子栅格Si,比较δi和δavg的大小。若δi≤δavg,则按式(3)将该栅格的权重设置为wi;若δi>δavg,则将该栅格作为父节点,跳转至步骤2。重复步骤2~步骤4,直至当前四叉树的深度di等于设定的最大深度D,且所有深度的子节点都分配权重为止;
(3)
步骤5遍历四叉树每一个末端叶子节点,在该节点对应的栅格中随机生成ni=N×wi个维诺站点。
对于非正方形零件设计域,无法直接按照上述算法进行维诺站点采样,需要计算该设计域的正方形包围盒,将包围盒设为四叉树的根节点来启动算法。对于在包围盒内、零件设计域以外的区域,由于应力值为0,按式(3)计算的权重也为0,因此不会被分配维诺站点。
1.4 各向异性维诺图生成算法
1.4.1 各向异性维诺图
不同于欧式空间中定义的维诺图,本文的各向异性维诺图是在黎曼空间中定义的。设在方向场Θ(x,y)所描述的二维黎曼空间Ω中存在点集S={s1,s2,…,sn},其中si为S内任一点,称为维诺站点,它的维诺区域(胞元)vi(si)定义为:
vi(si)={q∈Ω|d(q,si)
(4)
其中:q为空间中的任意点,d(q,si)和d(q,sj)分别为在Ω中点q到维诺站点si和sj的距离。
由定义可知,维诺胞元vi(si)由距离站点si“最近”的所有空间点组成。因此,由站点集S定义的维诺图V(S)为所有站点对应的维诺胞元的并集,即
(5)
1.4.2 黎曼度量
为生成各向异性维诺图V(S),必须在黎曼空间Ω中计算距离d(q,si)。对于Ω中的任意两点q和p,从q点到p点的有向距离dq(q,p)可以定义为:
(6)
其中M(q)为q点处的正定度规张量矩阵。由于M(q)≠M(p),因此dq(q,p)≠dp(p,q),本文采用Ω上任意点p到随机站点si的有向距离来计算,即dq(q,si)。
对张量矩阵M(q)进行奇异分解[1],可得:
M(q)=ETUE,
(7)
(8)
(9)
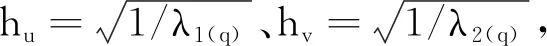

图3 黎曼椭圆
1.4.3 胞元择优方向生长策略

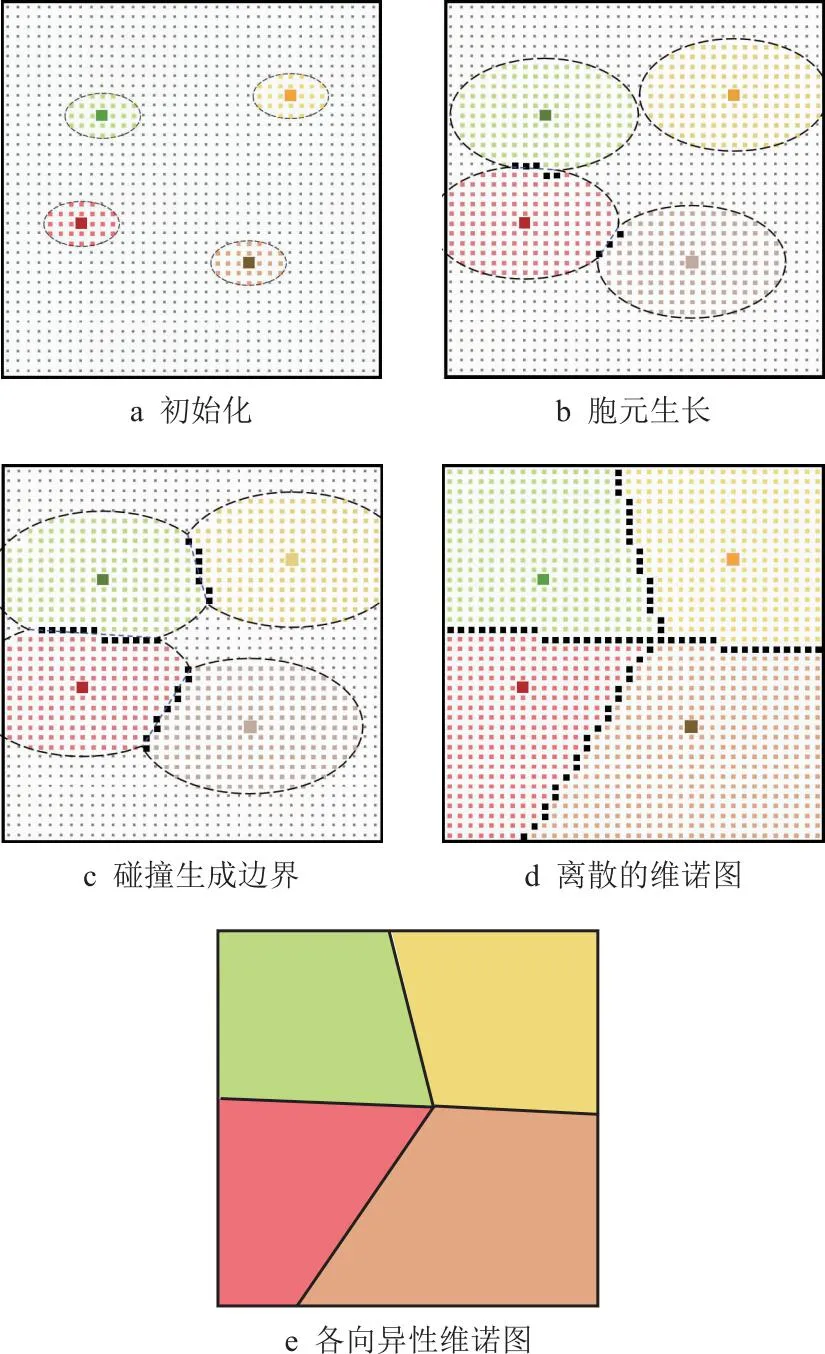
图4 维诺胞元的择优方向生长过程
基于胞元择优方向生长策略的各向异性维诺图生成算法的步骤如下:
步骤1将零件设计域D离散为一系列边长为a的正方形栅格,与1.3节中四叉树中最小栅格相同,以每个栅格的中心点表示该栅格。

步骤3遍历每一个未标记的栅格(中心点),判断该栅格是否在任意一个黎曼椭圆Ei内。若当前栅格仅在Ei内,则将该栅格添加到所对应的维诺胞元vi中,并标记该栅格;若当前栅格在多个黎曼椭圆内,则将该栅格添加到维诺边界B中。
步骤4对所有黎曼椭圆Ei沿短轴方向进行一次步长为a的生长,其他方向等比例生长,保证生长后的椭圆和原椭圆形状相似,角度不变。重复步骤2~步骤3,直至所有的栅格均被标记,并被添加到维诺胞元vi或维诺边界B为止。
在零件设计域内采用上述算法生成各向异性维诺图如图5所示。需要说明的是,算法输出的维诺图实际上是如同图4d的离散的维诺图,即维诺图的边界B和维诺胞元vi均是由离散的栅格中心点表达的,本文后续2.5D维诺多孔零件也是在这种离散的各向异性维诺图基础之上生成的。如图4e和图5的连续的维诺图是将维诺边界B中的栅格中心点拟合成光滑的曲线,从而生成连续的维诺边界,被边界分割包围的区域即维诺胞元。

图5 在零件设计域内生成各向异性维诺图
1.5 梯度各向异性维诺多孔零件
将各向异性维诺图的边界点通过偏置算法生成厚度为τ的内壁,并将维诺胞元内部掏空,生成2D维诺多孔结构,然后将对该结构进行拉伸,即可生成2.5D梯度各向异性维诺多孔零件(如图6c)。壁厚偏置算法的基本原理如图7所示。
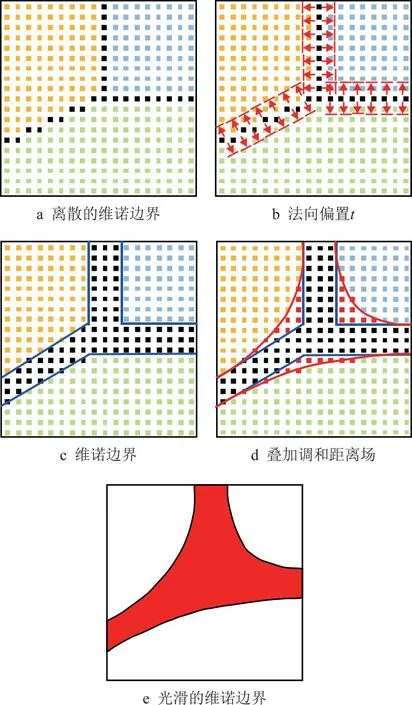
图6 壁厚偏置算法

图7 调和距离场光顺胞元Vi的维诺边
虽然采用维诺边界偏置生成维诺结构内壁的方法简单,但也会在支杆连接处生成尖锐的拐点,造成各向异性维诺多孔零件在这些尖锐部位形成应力集中(如图6所示),降低了多孔零件的力学性能。因此,需要对拐点处进行光滑处理,本文通过调和距离场算法来解决这一问题[19]。如图8所示为采用调和距离场来光顺维诺胞元vi的边界bi∈B的示意图。其基本思想是:将bi和vi中的离散点的距离场hp分别初始化为1和0,通过调和算子对满足要求的点进行反复迭代并归一化,最终使越靠近边界的点距离场值越趋近于1,反之则趋近于0。最后,将调和距离场hp>ρ的点都作为维诺边界(本文取ρ=0.8~0.9),即可以实现对原维诺边界的光顺。调和距离场算法如下。

图8 采用调和距离场算法对多孔零件进行光顺
算法1调和距离场算法。
输入:维诺胞元内部的离散点集vi,维诺边上离散点集bi,调和距离场控制参数γ。
输出: 调和距离场Δp。
for each p∈Bido
Δp←1; //初始化胞元边界点的距离场值为1
end for
for each p∈Vido
Δp←0; //初始化胞元内部点的距离场值为0
end for
whilep∈Viand hp<γ do //本文取γ=0.9
for each p∈Vido
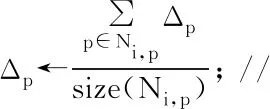
end for
end while
hp←Normalize(hp); //归一化调和距离场值
虽然对各向异性维诺图直接采用调和距离场算法也能生成一定厚度的多孔零件,但该算法按距离比例计算的,直接使用会导致多孔零件的内壁厚度不均匀,即较大的胞元壁厚大,较小的胞元壁厚小,从而难以对多孔零件进行几何结构和力学性能的精准控制。本文在对维诺图的边界进行偏置生成厚度为τ的均匀内壁后,再采用调和距离场算法对支杆接点处的拐角进行光顺,保证了多孔结构壁厚的均匀性。
需要注意的是,调和距离场的应用会使多孔零件的体积分数略微增加。如图8所示,该多孔零件采用调和距离场算法前后体积分数分别为62.7%和62.8%,仅增加0.1%。而通过有限元分析,可以得到光顺前后多孔零件的最大应力分别为53.25MPa和31.18MPa,光顺后最大应力降低了41.44%,说明调和距离场算法能够有效降低应力集中现象,提高多孔零件的力学性能。此外,调和距离场的引入还会略微增加多孔零件的设计时间。对于图8中的零件,算法生成光顺前的2D零件耗时158 s(硬件环境为Inter Core2 i5 CPU,16 GB内存与NVIDIA GeForce GTX 1650显卡的计算机),生成光顺后的2D零件耗时173 s,耗时增加9.5%。
2 维诺多孔零件的力学性能分析
2.1 影响因素
2.1.1 随机性
由于本文加权随机采样算法所生成的维诺站点具有随机性,即在零件相同应力分布条件下,每次运行加权随机采样算法都会得到不同的站点分布,导致生成的2.5D维诺多孔零件的内部结构不相同。为了评估这种随机性对多孔零件力学性能的影响,本文对某零件在相同条件下随机采样了4组不同的维诺站点,站点数量都为N=200,再按照本文算法分别生成4个壁厚相等的维诺多孔零件。采用ABAQUS软件分别对其进行有限元分析,结果如图9所示。可以看出,4个多孔零件的体积分数ω略有差异,最大和最小ω分别为64.5%和67.9%,波动率为5.0%;同样,零件的最大应力σmax也略有差别,最大和最小σmax分别为35.35 MPa和37.13 MPa,波动率为4.8%,说明加权随机采样算法导致维诺站点分布的随机性对维诺多孔零件的力学性能和体积分数影响不大。
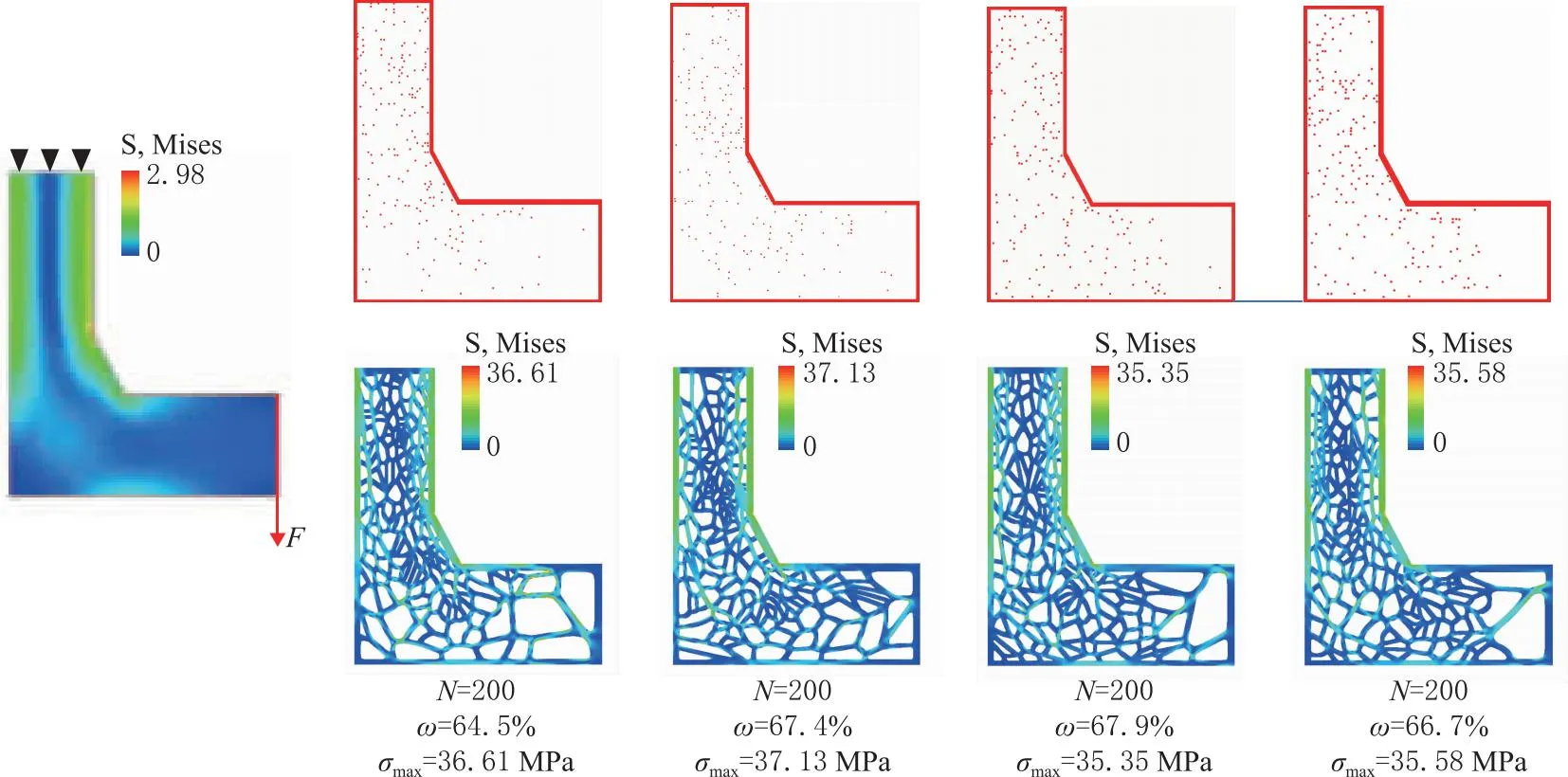
图9 维诺站点分布的随机性对多孔零件的影响
2.1.2 站点数量
在维诺零件的建模过程中,维诺站点的数量N是由设计人员根据经验设定的。为探究N的大小对维诺多孔零件力学性能可能造成的影响,对某零件在内部应力分布相同、且零件相对密度相当(通过调整壁厚τ)的情况下,改变N的取值(N=150,190,230,270,310,350),随机生成6种不同内部结构的维诺多孔零件,并采用ABAQUS软件对这些零件进行有限元分析,如图10所示。可以看出,在相对密度几乎相同(约为62.9%)的条件下,6个零件的最大和最小σmax分别为32.92MPa和30.01MPa,波动率为8.8%。结果表明,当在合理范围取值时,维诺站点数量N对维诺多孔零件力学性能的影响不大。这主要是由于影响维诺多孔零件力学性能的主要因素是体积分数ω而非维诺站点数量N。ω从宏观上决定着多孔零件的材料多少;当ω一定时,决定零件局部材料分配的则是各区域维诺站点数量的比例(相对值),即站点数量多的区域分配的材料多,反之则分配的材料少。
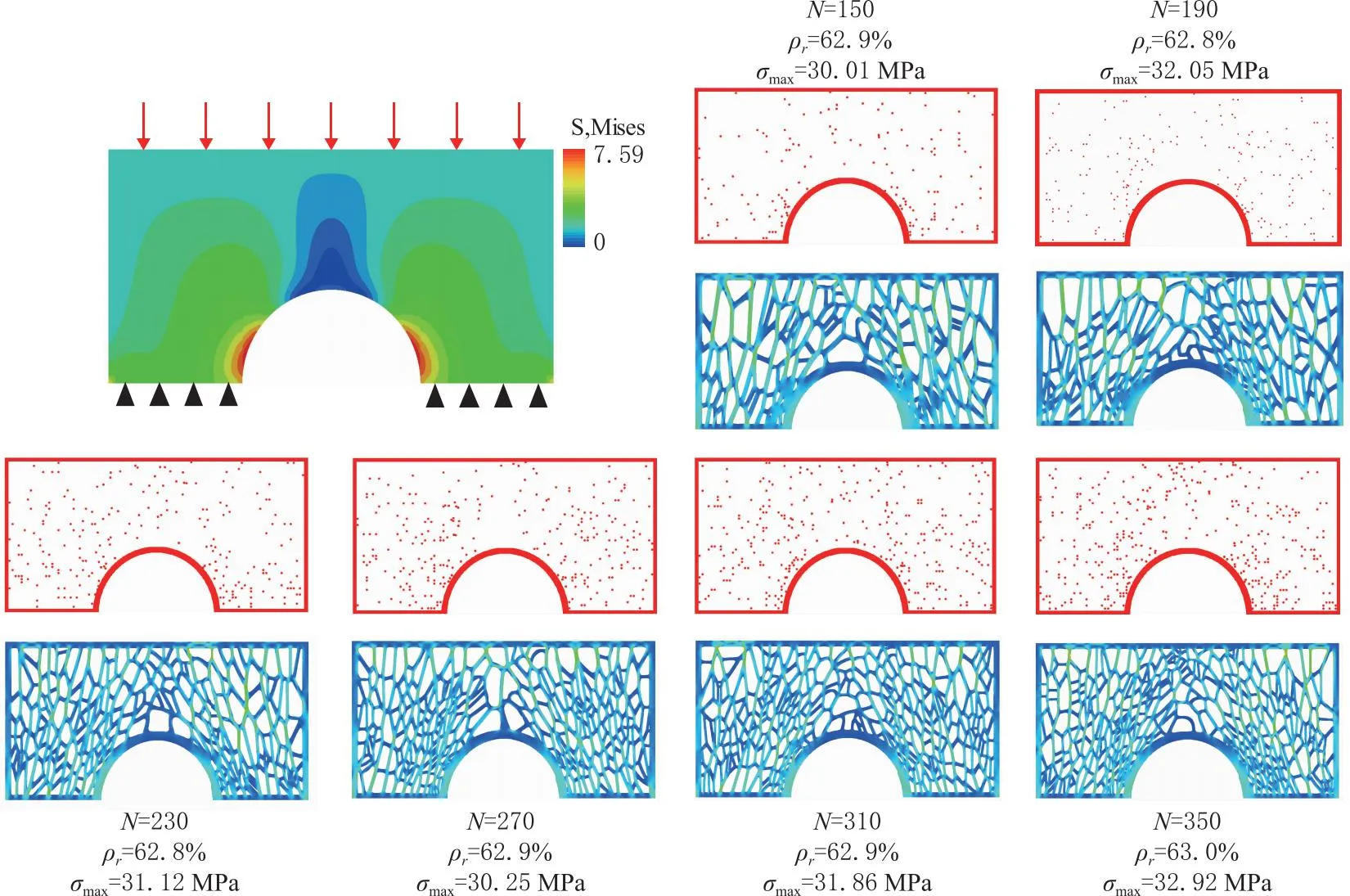
图10 维诺站点数量N对多孔零件力学性能的影响
一般来说,N的取值由零件尺寸大小、几何形状和内部应力等的复杂程度决定。零件尺寸越大、几何形状越不规则、内部应力越复杂,N的取值越大;反之,N取值越小。虽然N的取值范围较为宽泛,但过小的N值会导致站点的分布不能匹配零件的应力梯度,从而在零件打印时影响局部材料的分配,导致多孔零件力学性能下降或材料的浪费;过大的N值虽然提高了站点分布与零件应力分布的匹配度,但同时也增加算法的时空复杂度,并导致维诺胞元尺寸过小、壁厚过薄,甚至超过3D打印机的打印极限,影响零件的打印精度。由于本文中的零件尺寸都在50mm~150mm范围内,根据零件的复杂程度和应力状态,N的取值区间为[100,400]。
2.2 不同多孔结构的性能对比
为进一步验证本文算法所生成的梯度各向异性维诺多孔零件在力学性能方面的优越性,设计了如表1所示的有限元分析实验,将其与均匀各向同性、梯度各向同性维诺多孔零件进行对比。其中,均匀各向同性维诺多孔零件的维诺站点是在设计域内均匀分布,且设计域内各点hu∶hv=1,黎曼椭圆退化为圆,按照本文生长算法生成均匀各向同性的维诺多孔零件;梯度各向同性维诺多孔零件的维诺站点是在设计域内按照应力标量场σ(x,y)加权随机采样的。
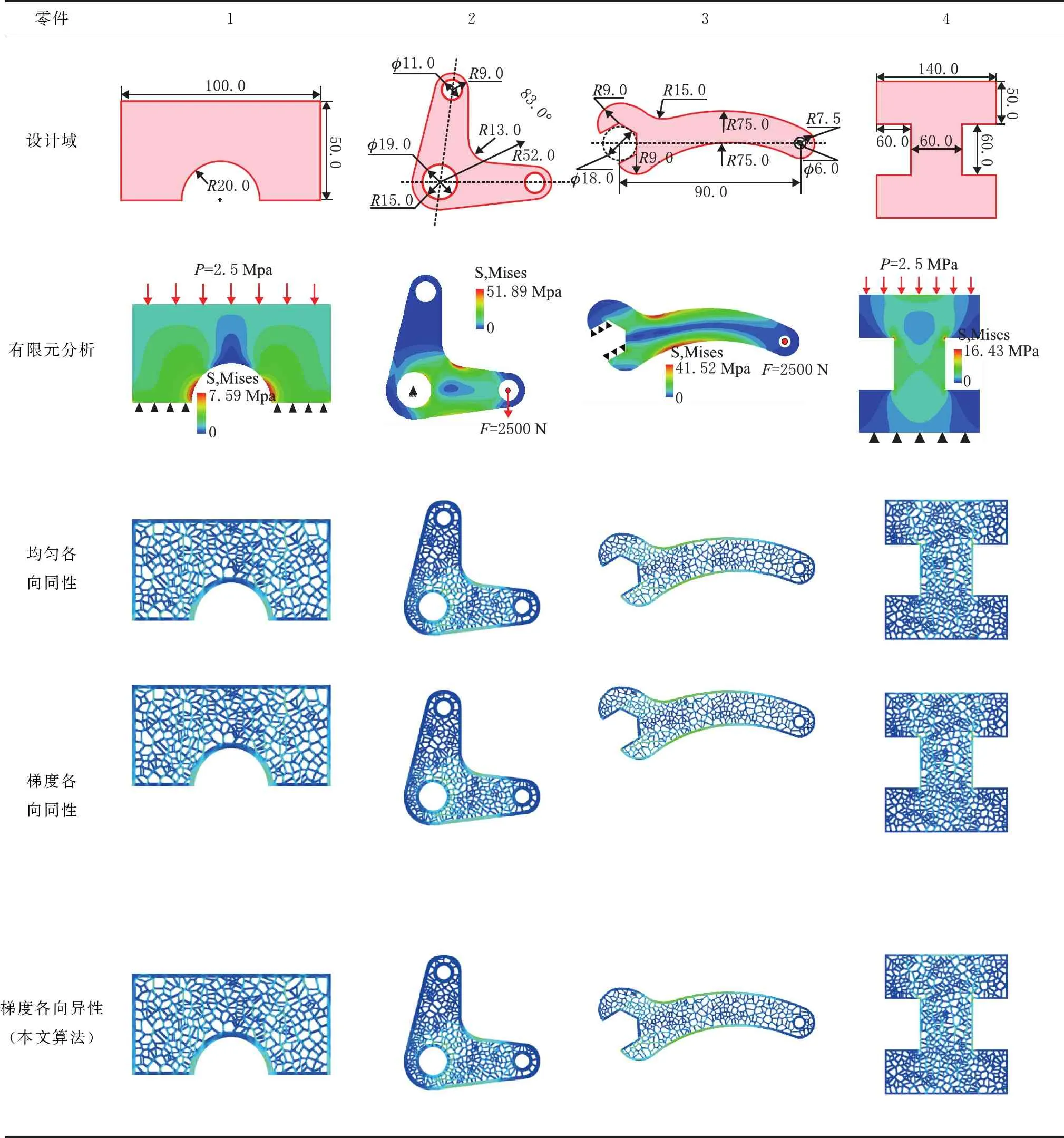
表1 三种多孔零件的有限元分析对比
从表2的对比分析结果可以看出,当同种零件的3种不同结构体积分数基本相同(波动不超过1%)时,梯度各向同性相比均匀各向同性,4种零件的最大应力σmax分别降低了10.18%、35.47%、5.10%和28.69%。说明通过应力驱动的维诺站点加权随机采样算法,使梯度多孔结构的材料分布更加合理,其力学性能梯度与应力分布的匹配度更高,即应力较大的区域分配较多材料(站点密集),应力较小的区域分配较少的材料,从而提升多孔零件的力学性能。而相对于前两种多孔零件,按本文算法设计的梯度各向异性维诺多孔零件表现出更优秀的力学性能。与均匀各向同性相比,梯度各向异性维诺多孔零件的最大应力σmax分别降低了37.80%、43.30%、35.42%和28.69%;与梯度各向同性多孔零件相比,其最大应力也有不同程度的提升。其原因在于通过各向异性设计,能在微观上控制材料更多的沿主应力方向分布,以牺牲其他方向性能为代价,提升其在主应力方向上的力学性能,从而抵抗形变和失效。结果表明:提升多孔零件力学性能有两种途径;①将材料按应力大小进行梯度分布;②将多孔结构的胞元按应力方向分布,实现各向异性。而按照本文算法设计的梯度各向异性维诺多孔零件能将上述两种途径较好的融合,从而大幅提升多孔零件的力学性能,实现零件轻量化设计。
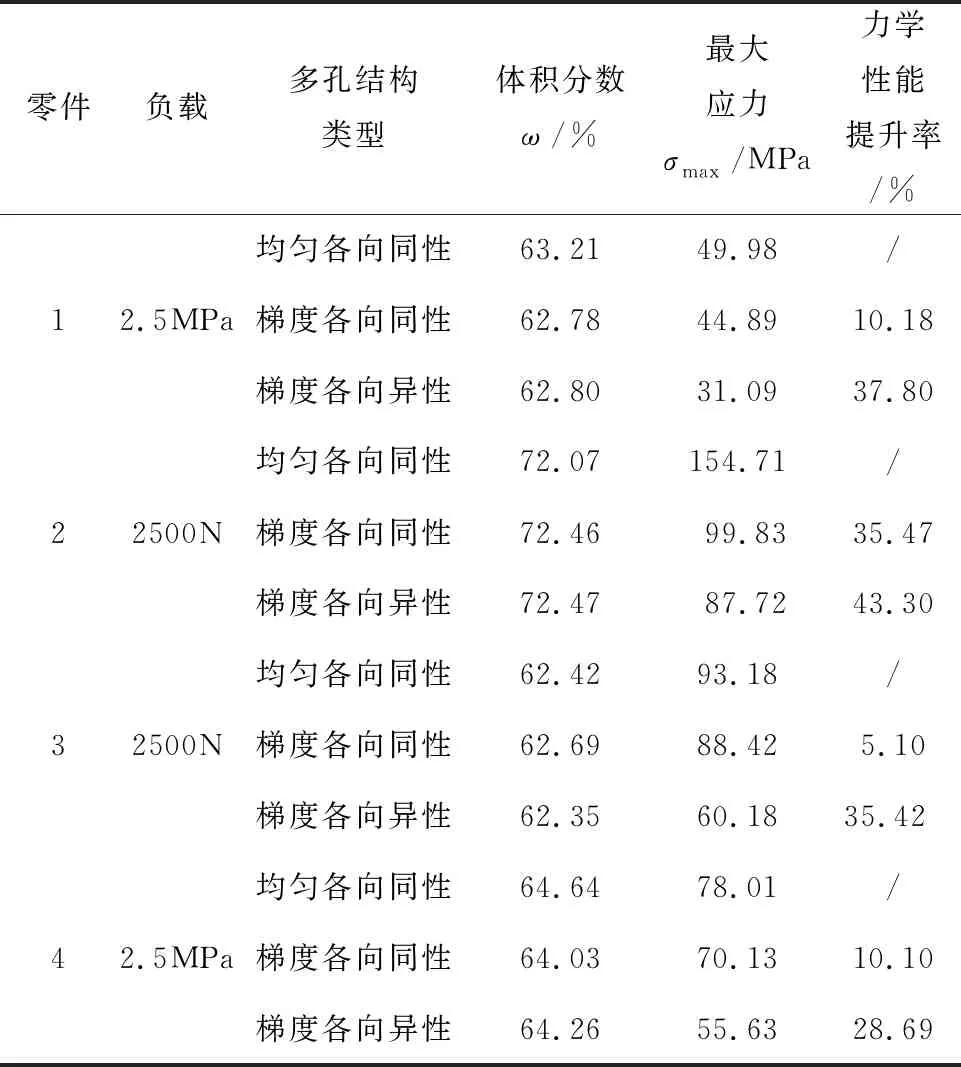
表2 有限元分析结果
2.3 多孔零件的力学性能实验
如图11所示为采用本文方法设计的梯度各向异性维诺多孔梁的建模过程。首先,对处于三点弯曲工况下的梁进行有限元分析,得到如图11所示的应力标量场σ(x,y)和如图11所示的应力方向场Θ(x,y)。设置站点数N=350,通过加权随机采样算法将σ(x,y)映射为设计域内的维诺站点分布,如图11c所示。在应力方向场Θ(x,y)对应的二维黎曼流形内,根据胞元择优方向生长策略生成梯度各向异性维诺图。最后,采用偏置算法和调和距离场算法,生成壁厚为t=0.8mm的梯度各向异性维诺多孔梁,如图11d所示。多孔梁模型的轮廓尺寸为100×20×10mm3,体积分数为65.5%。为进行对比实验,本文还设计了基于梯度晶格结构[20]、增强型k-nearest算法[1]、均匀各向同性维诺结构和梯度各向同性维诺结构的4种尺寸相同的多孔梁(分别如图11e~图11h所示)。其中,图11f~图11g三种多孔梁的站点数量、壁厚均和图11d所示的梯度各向异性多孔梁保持一致,体积分数近似相等。

图11 应力驱动的梯度各向异性多孔梁建模
采用SLM 3D打印机将上述5种零件打印成型并进行热处理,如图12a所示。打印材料为316L不锈钢粉末,热处理工艺为在温度为650°的保温箱内保温2小时后室温冷却。采用微机控制电子万能试验机(型号:ETM504D)对试件做三点弯曲实验,如图12b,速率设置为2 mm/min、最大位移为15 mm。实验测得的5种多孔梁的力——位移曲线如图12b所示,其余测试结果如表3中所示。

表3 三点弯曲实验结果

图12 多孔梁的三点弯曲实验
从三点弯曲实验结果可以看出,均匀各向同性多孔梁的力学性能最差,其他4种多孔梁由于进行了梯度和各向异性设计,其力学性能都明显优于均匀各向同性多孔梁。除梯度晶格梁外,按照本文算法设计的应力驱动的梯度各向异性维诺多孔梁结构的力学性能最好,说明其内部力学性能梯度与实际应力分布的匹配度更好。此外,梯度晶格梁在实验过程中达到设置的最大位移15 mm仍未发生断裂,但从图12c可以看出,其断裂峰值应力预计会大于梯度各向异性维诺多孔梁结构,而其抗弯强度则会小于后者。相较于均匀各向同性多孔梁,在重量差别不大的情况下(增加2.2%),其断裂峰值力、抗弯强度、弯曲模量分别提升了39.12%、39.11%和27.78%;相较于基于增强型k-nearest算法的梯度各向异性多孔梁,分别提升了9.44%、9.43%、6.48%。实验结果进一步表明,按本文算法建立的梯度各向异性维诺多孔零件能够在宏观上实现材料按应力大小进行梯度分布,在微观上实现材料尽可能多的沿主应力方向分布,从而使多孔零件内部力学性能梯度更好地匹配其实际应力分布,在实现零件轻量化的同时,有效地提升了多孔零件的力学性能。
为研究多孔零件的抗拉性能,根据应力场建立了标准拉伸件的梯度各向异性维诺多孔模型,如图13a所示。此外,本文同样设计了基于梯度晶格结构、增强型k-nearest算法、均匀各向同性维诺结构和梯度各向同性维诺结构的4种标准拉伸件作为对比,其建模过程如图13a所示。5种零件同样采用SLM 3D打印机和316L不锈钢粉末成型,热处理工艺为在温度为650°的保温箱内保温2小时后室温冷却,如图13b所示。采用ETM504D电子万能试验机对5组试样分别做拉伸实验,如图13c,速率设置为1 mm/min。实验测得的力-位移曲线如图13d所示,其他测试结果如表4中。

表4 拉伸实验结果

图13 拉伸实验
从表4所示的拉伸实验结果也可以看出,按照本文方法设计的梯度各向异性维诺多孔零件的几项拉伸性能指标均优于其他4种零件。相对于均匀各向同性维诺多孔零件,其断裂峰值应力、抗拉强度、拉伸模量分别提升20.98%、20.91%和18.26%;相较于基于增强型k-nearest算法的梯度各向异性多孔零件,分别提升了4.71%、4.21%和10.13%。该结果也表明:采用本文方法设计的梯度各向异性维诺多孔零件的内部力学性能梯度与实际应力分布的匹配都更高,能在有效提升多孔零件力学性能的同时,实现轻量化设计。
2.4 应力驱动的多孔零件轻量化设计
在进行多孔零件轻量化设计时,若零件受力方式相同,仅负载大小发生变化,零件内各区域应力值也会成比例放大或缩小,使得加权随机采样算法中各区域的权值保持不变。当维诺站点数量N恒定时,维诺站点的分布和最终生成的维诺多孔结构仅受随机性影响,而不随负载的不同而变化。此时,可以通过调整多孔零件壁厚t的大小,使多孔零件满足工程应用需求。
如图14所示为某C型夹头的轻量化设计过程,其轮廓尺寸和受力状态均标注在图中。零件材料为316L不锈钢,屈服强度为σs=450 MPa。当设均布载荷P=2.5 MPa时,通过ABAQUS软件对实心零件进行有限元分析,最大应力为121.28 MPa,远小于材料屈服强度σs,造成材料浪费,因此需要进行轻量化设计。基于有限元分析得到的应力场,采用本文算法生成站点数为N=350的梯度各向异性维诺多孔零件。为了选择合适的多孔零件,通过改变多孔结构的壁厚t=nτ(其中,τ=0.4 mm,n∈[2,8]),生成了一系列不同壁厚的维诺多孔零件。假设安全系数为λ=2.0,即所设计多孔零件的最大应力应该满足σmax<σs/λ=225 MPa。从图14可以看出,选择t=1.2 mm的多孔零件,其最大应力为220.69 MPa满足设计要求,而该多孔零件的体积分数仅为原零件的60.8%,材料使用率降低了39.2%,实现了轻量化设计。需要注意的是,t=1.2 mm并非该多孔零件壁厚的最优解,可以进一步降低t的取值,使σmax=σs/λ来获取最优零件设计方案。

图14 某C型夹头零件的轻量化设计
3 结束语
本文提出一种应力驱动的梯度各向异性多孔零件建模方法,实现了2.5D零件的轻量化设计。首先,通过有限元分析,获得零件设计域内的应力标量场和应力方向场。然后,采用加权随机采样算法,将应力标量场映射为维诺站点分布;提出一种基于胞元择优生长策略的各向异性维诺图生成算法,叠加应力方向场,在零件设计域内生成梯度各向异性维诺图。在此基础上,通过维诺边界偏置算法与调和距离场生成光滑的梯度各向异性维诺多孔零件。最后,通过有限元、三点弯曲实验和拉伸实验等对维诺多孔零件的力性能进行分析和对比。实验结果表明:①本文提出的应力驱动的梯度各向异性多孔零件设计方法具有较高的设计自由度,能较好的实现多孔零件内部力学性能梯度与实际应力分布的匹配度;②材料的梯度分布和各向异性均能有效提升多孔零件的力学性能,而本文方法能较好地融合上述两方面,提升多孔零件的力学性能,实现零件的轻量化设计。未来将探索应力驱动的梯度各向异性三维维诺多孔零件的建模方法,以及壁厚、站点数、体积分数和多孔零件力学性能之间的复杂耦合关系。
