基于贝叶斯优化神经网络的螺栓松动特性预测
2024-04-10韩帅帅孙清超
王 灿 ,韩帅帅 ,孙清超
(1.大连理工大学 机械工程学院,辽宁 大连 116023;2.江苏徐工工程机械研究院有限公司,江苏 徐州 221004)
0 引言
螺栓连接具有连接稳固性强、使用成本低、互换性好等一系列特点,常用来保障被连接结构之间可以有效地传递力和运动,据统计在航空航天、汽车、工程机械等制造行业中,螺纹连接大约占所有连接方式的68%[1]。螺纹松动是螺栓连接最常见的失效模式,松动机理及松脱的预测已成为工程应用中保障螺栓连接质量和可靠性的重要研究方向之一[2]。
大量的理论研究和工程实践表明,预紧力是保障螺纹连接接触刚度和可靠性的关键,本文认为螺纹连接松动指的就是螺纹连接预紧力的衰减[3],螺栓的松动分为非旋转松动和旋转松动。非旋转松动主要和界面接触特性以及材料特性密切相关,界面接触特性主要包括表面嵌入、微动磨损和应力再分布;材料特性主要包括蠕变、应力松弛和塑性变形;旋转松动是指螺纹连接在受到外部横向载荷作用下螺栓的局部滑移更容易导致预紧力的持续下降,是导致螺栓旋转松动的主要原因。YOKOYAMA等[4]建立了横向振动条件下螺纹连接力学的解析模型,发现螺栓的倾斜会影响局部滑移累积。DINGER[5]采用有限元仿真和试验的方法研究了扭转与横向振动载荷耦合作用下的局部滑移累积行为,将松动转速0.01°/周期作为是否发生旋转松动的依据。GONG等[6]建立了描述螺纹面局部滑移累积的改进Iwan模型,实现了对局部滑移累积的理论建模,得出了沿螺纹面径向方向的分力FR是导致螺纹面局部滑移累积的主要分力类型,抑制螺纹面沿径向方向的相对滑移是防止旋转松动的主要手段[7]。美国奥克兰大学NASSAR等建立了描述螺纹连接预紧力和摩擦力矩关系的线性[8-10]及非线性模型[11-13],基于横向振动试验,发现横向力(横向振幅)比较小时,预紧力可能保持不变,即存在旋转松动的临界横向力,并研究了不同因素对旋转松动临界横向力的影响规律。临界横向力/横向振幅是螺栓松动的分界点,当外界的振幅/力>临界点时,残余预紧力降低到接近零,螺栓出现松动,当外界的振幅/力≤临界点时,残余预紧力达到稳定值,螺栓连接系统稳定,本文认为在螺栓不发生疲劳断裂的情况下,在一定范围内残余预紧力越高,防松越稳定。在螺栓松动预测方面,阳光武等[14]建立螺栓松动线性累积模型,通过试验测量特定螺栓的位移幅值-松动寿命(D-N)曲线及表达式,利用D-N曲线和螺栓松动线性累积模型,对螺栓松动寿命进行预测。刘志峰等[15]提出利用BP(back propagation)神经网络建立预测特定工况下螺栓残余预紧力的方法,以残余夹紧力的百分比作为输出,将试验数据导入神经网络模型进行训练,训练完成后的神经网络模型可以预测特定工况下螺栓的残余夹紧力。王琳涛[16]等人提出一种机理引导数据的螺栓连接松脱特性预测方法,建立了一种基于高斯过程回归的螺栓松脱特性预测模型,为螺栓松脱特性准确预测提供了保证。张明远[17]建立了考虑螺纹面磨损深度变化的螺栓连接结构刚度模型,采用数值迭代计算仿真模拟横向载荷作用下螺纹面磨损引起的螺栓松动过程。然而,目前预测模型使用工况受限、预测精度不高的问题,难以满足制造需求。
本文将机理模型和数据模型相互融合,基于机理模型采用响应曲面法获取螺栓松动的关键因子,通过叶贝斯优化的神经网络算法建立螺栓松动和特征之间的全连接层,建立了高精度螺纹连接松动预测模型。该模型考虑了松动过程的分散性和非线性等特点,可以预测螺栓预紧力在不同振幅等工况下残余预紧力的大小,能够更加准确地反映螺纹连接的松动,为螺纹连接结构工程实践中的维护和保养提供指导。
1 螺栓松动机理分析
螺栓拧紧后力矩示意图如图1所示,在拧紧力矩撤销之后,螺栓沿其轴线方向受到螺距扭矩Tp、端面扭矩Tb以及螺纹扭矩Tt三个力矩作用。其中Tp是导致螺栓向着松脱方向回转的扭矩,Tb和Tt则起到抵抗螺距扭矩Tp的作用。在连接结构不承受外部载荷或者外部载荷较小的情况下,3个力矩达到平衡,此时螺栓的回转角加速度为零;当外部载荷较大时,Tb和Tt会随之下降,当两者之和降低到不足以抵抗螺距扭矩Tp时,螺栓的回转角加速度大于零,回转角速度增大;值得注意的是,当外部载荷从较大数值降低到较小数值之后,角加速度出现负值,回转角速度减小。其中,角速度减小的过程与其增大的过程计算方法一致,符号相反,为了方便描述,本文重点讨论回转速度增大的过程。
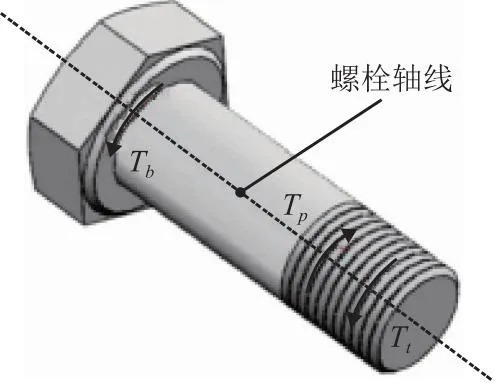
图1 螺栓拧紧后力矩示意图
文献[18]给出了Tp、Tb和Tt的数值计算方法,如式(1)~式(6)所示。
(1)
(2)
(3)

(4)

(5)
其中:F表示连接结构预紧力,Fbs表示螺栓头部受到的横向载荷,P表示螺纹螺距,μb和μt分别代表端面摩擦系数和螺纹摩擦系数,qb0和qt0分别代表端面平均压强和螺纹面平均压强,ri与re分别代表端面最小接触半径与端面最大接触半径,rmin与rmaj分别代表螺纹最小接触半径与螺纹最大接触半径,r代表螺纹公称直径的一半,θ代表极坐标之下的角度变量,α和β分别代表螺纹牙型角的一半和螺纹导程角,ηb=vbl/ωb和ηt=vtx/ωt分别代表端面平动-转动速度的比值和螺纹平动-转动速度的比值,RTb和RFb是关于ηb的定积分数值,RTt和RFt是关于ηt的定积分数值。
回转角速度ω如下:
(6)
其中ω0为t时刻的回转速度。回转角位移如下:
(7)
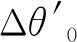
(8)
其中kb和kc分别代表螺栓和被连接件的刚度。
由式(1)~式(5)与式(8)可得出,影响螺栓的松动因子主要有端面摩擦系数、螺纹摩擦系数、横向力/横向振幅、初始预紧力、螺距、刚度、螺栓头下接触面积等参数。
2 螺栓松脱影响因子敏感度分析
2.1 松动因子横向振动试验
机理模型只能对因子进行定性的分析,很难对各个因子对螺栓松动的影响敏感度进行定量分析。本文以螺栓横向振动实验数据为基础,采用响应曲面法分析因子对残余预紧力的敏感度,实验数据由横向振动实验台获取,试验台如图2所示,主要由固定板、移动板、液压加载机构(伺服阀、推力油缸)驱动运动板实现横向的振幅/力加载,加载曲线为正弦曲线,从而引起螺栓松动,典型松动曲线如图3所示,阶段1约发生在早期的500个振动循环周期内,主要是由螺栓头下接触的嵌入损失、蠕变等导致的,阶段2是由螺栓、螺母发生转动导致的预紧力损失,残余预紧力随着振动次数的增加稳定在一定范围时,螺纹连接结构达到一个动态的平稳状态。
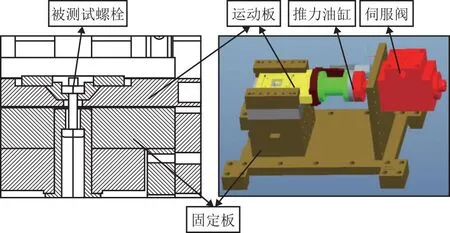
图2 横向振动试验台
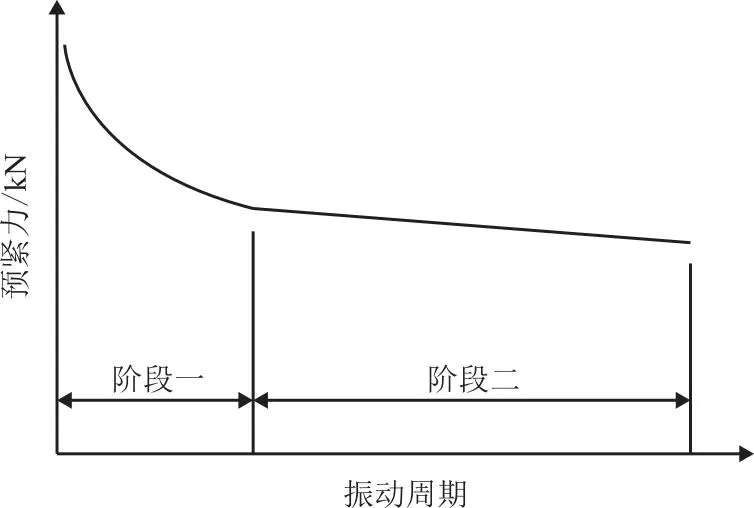
图3 典型松动曲线
结合参数的标准化程度,筛选初始预紧力、螺纹摩擦系数等5个因子,以螺栓为M14×1.5为研究对象,制定了需要进行敏感度分析的5个因子及试验水平,如表1所示。
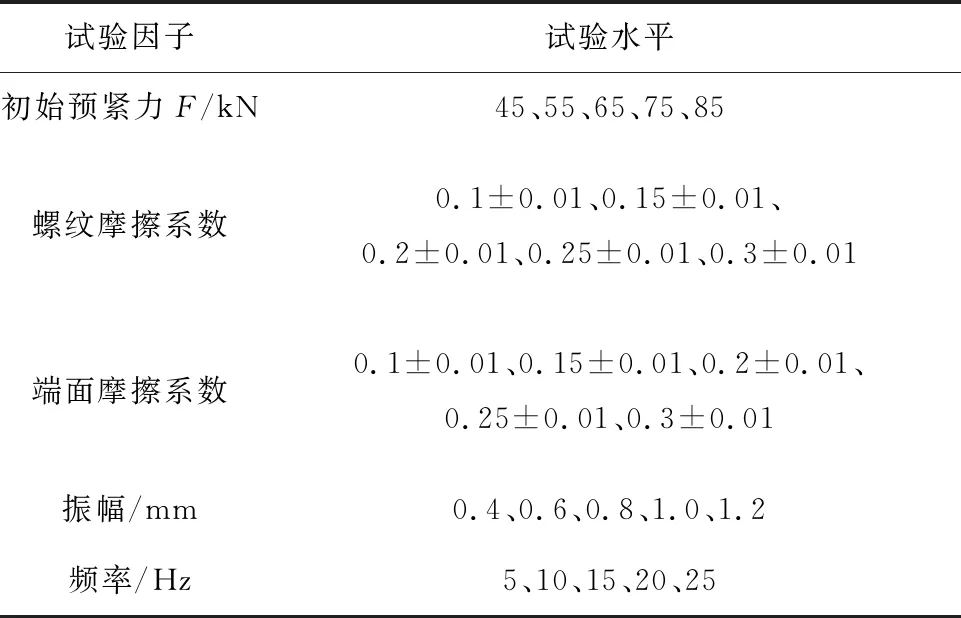
表1 试验因子及其试验水平
2.2 松动因子敏感度分析
响应曲面法(Respond Surface Methodology,RSM)是由BOX和WILSON共同提出的,是结合统计数学理论来分析复杂的耦合环境中多因素问题的实验方法[19]。 该方法利用合理的实验设计, 进行一系列,实验并针对该实验结果,建立连续变量曲面模型,对影响反应过程的因子及其交互作用进行评价。采用响应曲面法研究上述5个因子对螺栓残余预紧力的二阶响应曲面的影响,试验组数32组,每组测试5件取平均值,振动试验周期为4 000个循环。
从图4中可以看出,导致螺栓松动的单因子主要为初始预紧力和振幅两因素,频率、螺纹摩擦系数、端面摩擦系数对预紧力的影响较低。螺栓松动的影响因子交互后,从图5中可以看螺纹摩擦系数、端面摩擦系数、频率、初始预紧力均与振幅之间的交互作用显著,其余因素之间交互作用不明显,对残余预紧力影响不大。通过主效应图和交互作用可以明确影响螺栓松动的关键因子为振幅、初始预紧力,其次为螺纹摩擦系数、端面摩擦系数、频率。工程机械容易松动的部位表面粗糙度较高,端面摩擦系数大,螺纹摩擦系数较小,振动频率大约在10~20 Hz,在后续的松动模型预测方面选取螺纹摩擦系数0.1,端面摩擦系数0.3,频率15 Hz对残余预紧力进行预测分析。
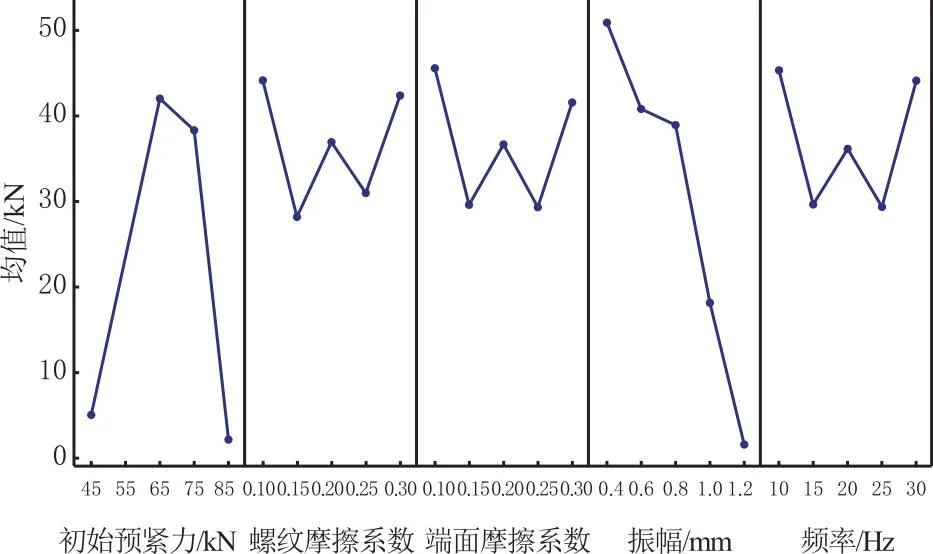
图4 残余预紧力单因子主效应图

图5 因子交互作用分析
3 数据驱动的螺栓松动预测模型
3.1 神经网络预测模型
螺栓松动过程具有非线性、不确定性的特点,常规数学模型推导过程繁琐且预测精度难以满足使用要求。神经网络算法具有分类的准确度高,并行分布处理能力强,对噪声神经有较强的鲁棒性和容错能力,能充分逼近复杂的非线性关系,并且能干处理小样本、非线性等复杂问题[20],因此选用神经网络算法开发残余预紧力预测模型具有较高可行性。然而神经网络需要大量的超参数设置,如全连接层数、全连接层大小、激活函数、正则化强度等,被调整的超参数的数量以及每个新的超参数集合的计算复杂度使得神经网络参数的选择变得十分繁琐。贝叶斯优化算法是一种对黑盒目标进行全局优化的方法,当目标函数评估困难且计算复杂时尤为适用,并优于网格搜索和随机搜索等其他全局优化算法[21-23],可以对螺栓松动非线性、不确定性的特点进行较好的描述,因此本文选用贝叶斯优化算法建立神经网络预测模型。基于贝叶斯优化的神经网络预测模型训练步骤如下。
(1)采集螺栓松动数据,共计380条,选取残余预紧力作为模型输出,初始预紧力、螺纹摩擦系数、表面粗糙度、振幅及频率为输入,分配训练集和测试集样本,分配比例为95%:5%;
(2)利用贝叶斯全局优化算法优化神经网络超参数集,选定最小均方根误差(RMSE)为适应度函数,训练次数30次,通过贝叶斯优化的神经网络预测模型训练结果如图6所示。
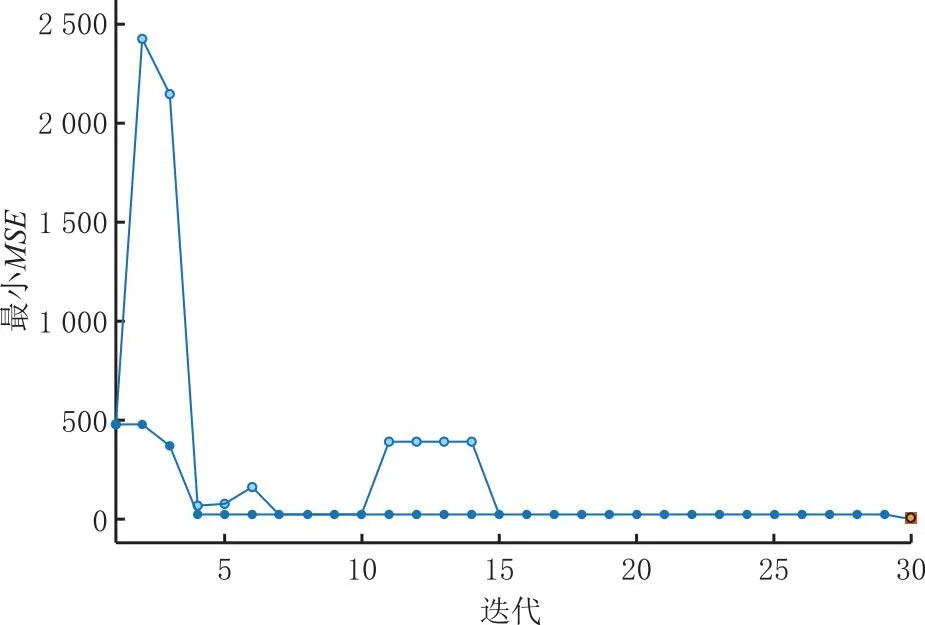
图6 基于贝叶斯优化的神经网络预测模型训练
(3)利用最佳参数集训练神经网络模型并使用该模型进行回归预测,优化后的模型结构如图7所示,该模型包括三层全连接层,其大小依次为99、263、2。模型正则化强度(Lambda)设置为0.021 984,采用Sigmoid型对数函数激活函数,函数单调递增且连续可导,可以把实数域光滑地映射到[0,1]空间,表达式如下:
(9)
为比较贝叶斯优化神经网络预测模型的优越性,选取未优化的三层神经网络、高斯过程回归以及支持向量机作为对比模型,采用均方根误差和决定系数(R2)为评价指标,其数学表达式如下:
(1)均方根误差(RMSE):
(10)
(2)决定系数(R2):
(11)

对比上述4种模型在不同振幅下的螺栓残余预紧力箱型图(如图7)可知,所有的预测模型均没有离群点,满足预测需求。观测不同振幅下预测值中位线可知,基于贝叶斯优化的神经网络预测模型在所有振幅下均与真实值的吻合度较高,而未优化的三层神经网络及高斯过程回归模型在0.6mm及1.2mm振幅下的预测值较真实值偏低,支持向量机的吻合度相对较差,仅在高振幅(大于1mm)条件下保持较好的预测精度。
均方根误差和决定系数对比表如表2所示,可知优化后的神经网络均方误差最小,且R2系数最接近1,相比于未优化的三层神经网络、高斯过程回归以及支持向量机模型均方根误差分别降低47%、63%、67%。因此基于贝叶斯优化的神经网络预测模型可以更加可靠的对螺栓松动情况进行预测。

表2 不同模型下的预测效果评价表
3.2 螺栓松动预测
利用已建立的模型预测不同振幅、初始预紧力下螺栓残余预紧力分布情况,当螺纹摩擦系数为0.1±0.01,端面摩擦系数为0.3±0.01,振动频率为15Hz时,预测结果如图8所示。可以发现,随着振动幅度的增加,残余预紧力整体呈下降趋势。在初始预紧力为45~75 kN区间时,初始预紧力与残余预紧力呈正相关,即初始预紧力越大,残余预紧力越大,防松效果越好。然而,当初始预紧力较大时(85 kN),残余预紧力随着振动幅度的增加而急剧下降;当振动幅度高于0.63 mm时,其残余预紧力不足50 kN,防松效果低于同等条件初始预紧力为75 kN的使用工况。当振动幅度继续增加至0.7 mm时,其防松水平低于初始预紧力为65 kN,继续增加振幅至1.0 mm时,螺栓残余预紧力为0 kN,即螺栓发生松动。大预紧力下螺栓残余预紧力随着振动幅度增加而大幅度下降的原因是螺栓的初始预紧力过高,导致在振幅高于0.63 mm时,螺栓出现疲劳损伤,其残余预紧力出现急速的衰减。
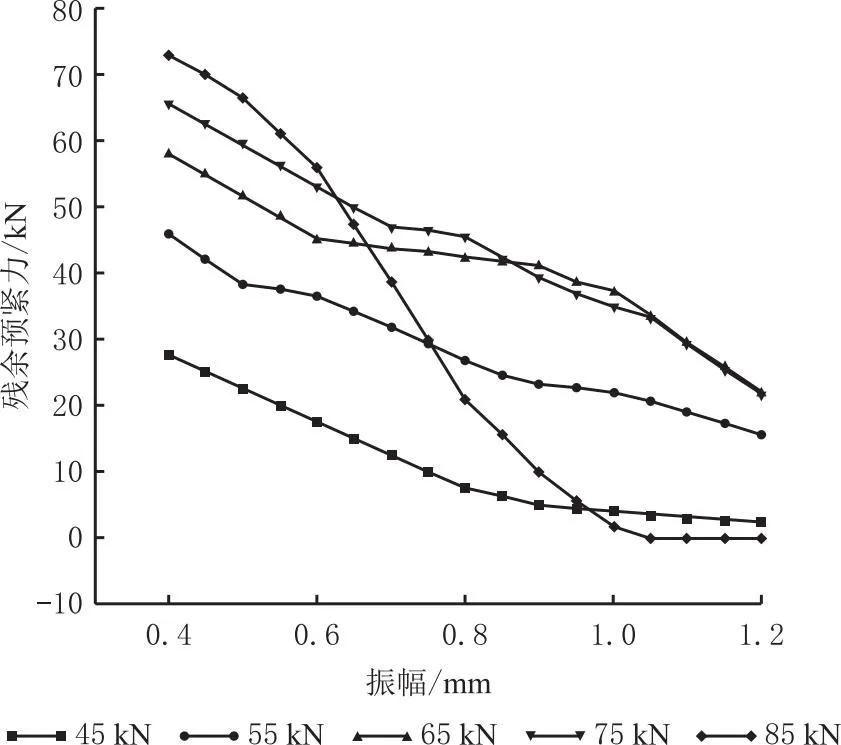
图8 不同振幅、初始预紧力条件下螺栓残余预紧力预测情况
4 典型连接部位松动试验验证
采用紧固件分析系统对螺栓的螺纹摩擦系数和端面摩擦系数进行测试分析(如图9),以M14×1.5-10.9级螺栓为对象,螺纹涂抹二硫化钼,测试方法参照ISO 16047,螺纹摩擦系数为0.1~0.11,端面摩擦系数0.29~0.3,保证摩擦系数的实验测试与预测的一致性。以8个螺栓(M14×1.5)为例,如图10所示,通过振动试验来验证残余预紧力预测的准确性,采用超声波对螺栓的预紧力进行检测,振动加载为正旋加载,振幅分别为0.7 mm、0.8 mm、0.9 mm、1.1 mm,频率为15 Hz,振动过程预紧力衰减数据如图11所示,随着振幅的增加,非旋转松动导致的预紧力衰减也急剧增大,与文献[24]得出的非旋转松动预紧力的急剧衰减主要是由微动磨损、应力再分布和塑性变形在周期性的横向载荷作用下导致的结论是一致的,预紧力经过2 000个周期的振动后,残余预紧力的值都达到了一个稳定的状态,也间接证明了存在一个临界振幅,在外部载荷未超过临界振幅时,松动未发生,与文献[25]所假设的存在一个临界位移是一致的。经过2 000个循环的加载后,最终残余预紧力测试数据如表3所示。
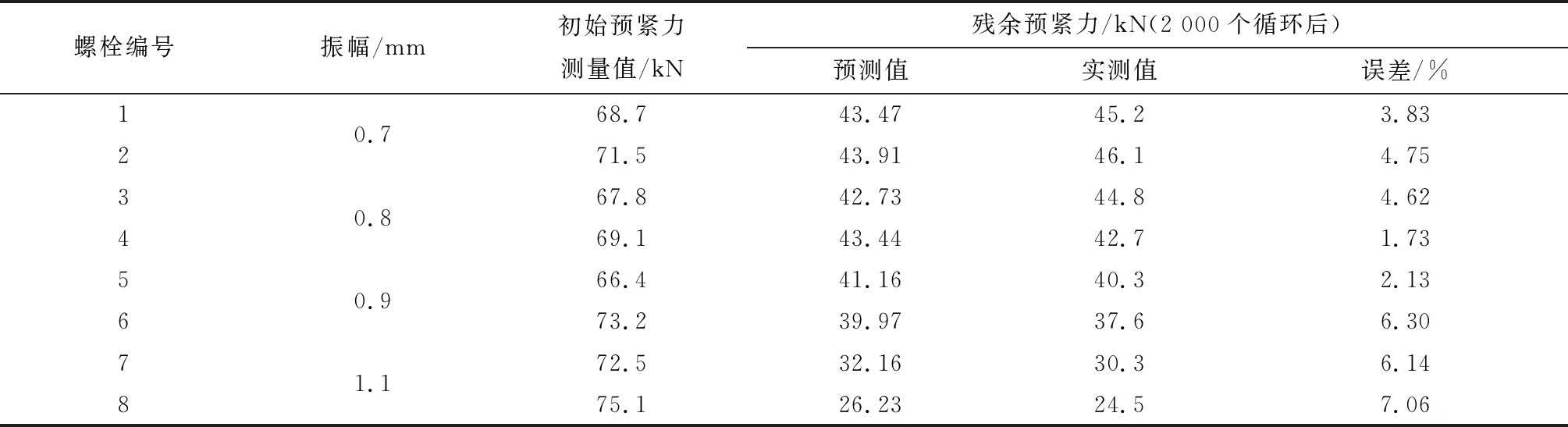
表3 残余预紧力预测值及实际值

图9 紧固件分析系统
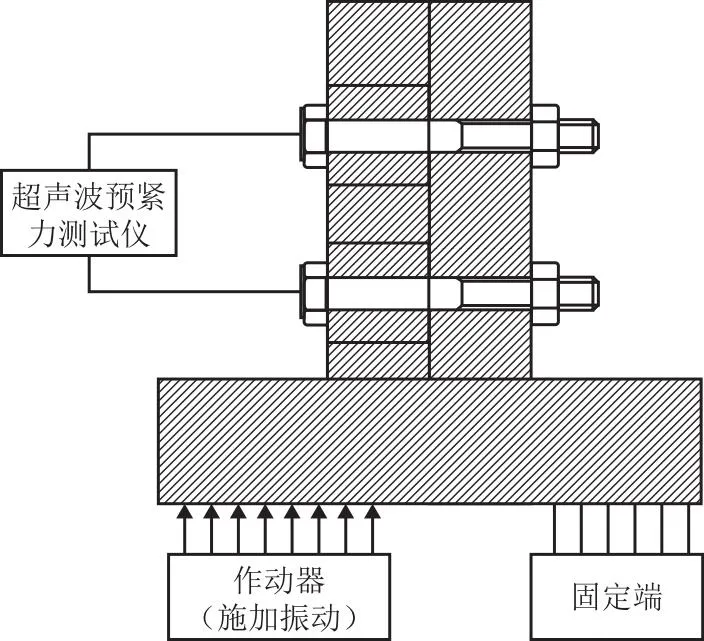
图10 多螺栓振动示意图
残余预紧力>40 kN时,预测的误差为1~4%,当残余预紧力<50 kN时,预测的误差为6~7%,为实际的工程应用提供了理论参考和数据支撑。但需要指出的是,随着螺栓规格的改变,螺栓预紧力的衰减趋势相同,但残余预紧力预测误差与预测模型和数据的精准度都有很大的关系,其普遍性还需要进一步的研究。
5 结束语
针对螺栓残余预紧力无法精准预测的问题,本文开展了基于机理模型和数据模型联合的预测方法,实现了螺栓残余预紧力的精准预测,并得到以下结论:
(1)基于响应曲面法构建了螺纹松动机理模型,通过交互作用分析,螺纹摩擦系数、端面摩擦系数、频率、初始预紧力与振幅之间的交互作用显著,结合主效应分析,明确了振幅、初始预紧力是螺纹松动的敏感因子。
(2)建立了基于贝叶斯优化的神经网络预测模型,确立了模型最优超参数,相比于未优化的三层神经网络、高斯过程回归以及支持向量机模型,其均方误差最小,且R2系数最接近1,可以更加可靠的对螺栓残余预紧力进行预测。
(3)通过试验验证,基于贝叶斯优化的神经网络预测的残余预紧力与实际测试值误差<7%,验证了模型的有效性和可靠性,满足制造需求。
未来可以进一步拓展该方法在不同工程领域中的应用,考虑更多复杂环境下的影响因子,推广到不同类型、不同拧紧方式的螺栓预紧力预测中去,以提高模型的普适性。同时,对于贝叶斯优化算法和神经网络结构的优化也是一个值得关注的方向,以进一步提升模型的准确性。
