智能电网中基于填充方法的双向拍卖电力资源分配方法

闫先国,孙碧颖,录鹏东,金鑫,史莹,桂小林

(1. 国网甘肃省电力公司数字化事业部,730000,兰州; 2. 西安交通大学电信学部,710049,西安)

随着社会经济的飞速发展,电力资源成为人们日常生活和社会发展极其重要的组成部分。从20世纪初开始,我国就结合本国的电力产业发展现状和电力用户用电特征,充分借鉴国际上各国先进的改革经验[1-6],探索出一条理论先进又符合实际的市场化改革道路[7-10]。电力市场交易双方存在博弈关系,这种博弈行为会影响社会整体的效益,引起市场价格的不合理波动,危害系统的运行效率。如何设计合理的电力市场竞争机制,是电力工业改革迫切需要解决的问题。

互联网技术和智能终端的快速发展,使得越来越多的新型技术被运用到传统的电力网络中,智能电网被不断普及[11]。智能电网的一个重要作用,就是对紧缺的电力资源进行合理、智能化的分配与再分配[12],通过智能电网技术,各电网系统之间可以通过协调,在电力紧缺的地区,实现电力资源的跨区域、低损耗的配送,使电力资源得到进一步合理配置,提高用电的安全稳定性[13]。

近些年来,一些针对电力资源的分配的研究大都采用动态规划方法,结合电力传输成本进行电力的一次分配[14-16],或优化实际电力资源的生产和分配过程中的固定成本、边际成本和启动成本以达到电力资源分配优化[17],都没有考虑电力资源分配与经济之间的关系。博弈论作为一种经济学理论,充分考虑了参与者之间的博弈关系,即相互影响、相互矛盾且具有决策自私性。博弈论在电力市场中也有所应用[18-19]。拍卖理论是博弈论的一种应用,在博弈论的基础上形成的一种交易方式,是现代经济学中的重要理论。由于我国在电力市场化改革初期的主要目标是实现“厂网分开,竞价上网”[20],因此围绕发电方的单向拍卖机制设计一直是研究的热点[21-26]。为数不多的使用拍卖机制且考虑买卖双方的电力资源分配研究也是使用多层次拍卖模型[27-29],更接近于通过耦合两个单向拍卖而实现双向拍卖,并没有真正实现双向拍卖,同时考虑买卖双方以及拍卖师的利益。

随着智能电网的发展,互动电网的概念被提出,通过构建互联数据网,推进电网消费者之间以及消费者和电网管理者之间的大规模互动。互动电网可以通过电子终端在用户之间、用户和电网公司之间形成网络互动和即时连接,实现实时、高速、双向的电力数据读取的总体效果,完成电力、电视、智能家电控制和电池集成充电等多用途开发,并且实现用户富裕电能的回售[30]。一些工厂或公司拥有自己的发电机,存在富裕电力时希望将多余的电力进行出售从而获得盈利,而在用电高峰期时某些工厂存在电力不足的情况,会影响收益。这时双方之间若能通过供电局进行电力的二次交易,实现用户富裕电能的回售,可以达到三赢的状态,避免出现区域性、季节性电力的短缺及局部地区电力过剩与局部地区电力短缺的情况。因此,本文提出了一种基于填充方法的双向拍卖机制,完成电力资源的二次配置。本文主要创新点如下。

(1)从经济学的角度设计了一种双向拍卖机制,激励拥有富裕电力的用户为电力紧缺用户提供电力资源,实现电力资源市场的真实双向拍卖,并满足预算平衡和个人理性。

(2)采用基于线性规划(linear programming,LP)的填充分配方法解决智能电网中的电力资源再分配,在多项式时间内得到接近最优的分配结果。

(3)采取基于关键值的定价策略和基于维克瑞-克拉克-格罗夫斯(Vickrey-Clarke-Groves,VCG)机制的定价策略,分别对买方和卖方进行合理定价,避免买卖双方潜在的预算不足,保证买方和卖方的真实性与个人理性。

(4)通过仿真实验验证,本文设计的双向拍卖机制保证了真实性、预算平衡以及个人理性,并且可以在多项式时间内得到近似最优解的分配结果。

1 双向拍卖模型及电力资源分配方法

1.1 双向拍卖模型

地方供电局作为边端,相较于端用户拥有更多的计算资源,可以完成赢家确定以及定价的计算任务,作为使用拍卖进行富裕电力回售时的拍卖师;拥有富裕电力资源的用户作为卖方,通过传统电力传输方式或移动充电方式为匹配到的买方用户提供电力资源。基于拍卖理论的电力资源分配应用场景如图1所示。

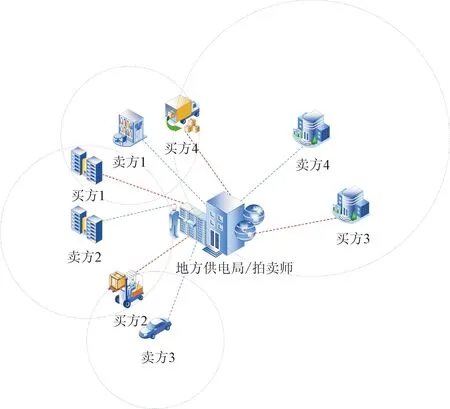
图1 基于拍卖理论的电力资源分配应用场景Fig.1 Application scenario of power resource allocation based on auction theory

存在多个拥有富余电力的卖方,每一个卖方都可以为有购电需求的买方提供电力资源。每个卖方出售的电力资源能传输的距离有限,因此每个出售富裕电力的卖方的服务范围是有限的,只能对其覆盖范围内的需要购买电力的买方提供富裕电力出售服务。地方供电局作为拍卖师,会收到多个买方的购电需求和多个卖方出售富裕电力的投标。

参与拍卖的角色如下。

(1)买方用户集合为I={1, 2, ,i, ,m},m为买方用户数量。每个买方i向地方供电局提交投标标的Bi={di,bi, (χi,δi)}。其中:di表示买方i想要购买的电力资源单位;bi表示买方i对其获得所需电力资源后所能带来价值的估价,即其为了获得相应的电力资源而愿意支付的最大货币成本量;(χi,δi)表示买方i的地理位置坐标,χi表示其所处地理位置的经度,δi表示其所处地理位置的纬度。买方i接收到地方供电局的拍卖结果后,从相应的卖方j处获得电力资源,并向地方供电局支付相应费用。在该模型中,电力资源是可分的,即每个买方的电力资源需求可以由多个卖方提供。为了简单起见,本文将电力资源表述为多个电力资源单位。

(2)卖方用户集合为J={1, 2, ,j, ,n},n为卖方用户数量。卖方j向地方供电局提交投标标的Aj={sj,aj, (γj,φj),λj}。其中:sj表示卖方j在此次拍卖中想要出售的富裕电力资源单位;aj表示卖方j对其想要出售的每单位电力资源的要价,即其获得每单位电力资源的最小货币成本量;(γj,φj)表示卖方j的地理位置坐标,γj表示其所处地理位置的经度,φj表示其所处地理位置的纬度;λj表示卖方j的最大可服务距离,因为电力资源在传输过程中存在损耗,因此卖方j只愿意为一定范围内的买方i提供富裕的电力资源。卖方j接收到地方供电局的拍卖结果后,为相应的买方i提供电力资源,并从地方供电局获得相应报酬。在该模型中,每个卖方都可以为多个买方提供电力资源,每个买方也可以从多个卖方处获得电力资源。

(3)地方供电局作为拍卖师,收集买方和卖方分别提交的标的,确定买卖双方的匹配和中标者,然后计算买方的支付价格和卖方的报酬。

1.2 确定供需匹配关系

考虑到在电能回售的过程中,电力传输时存在损耗,因此本文通过确定供需匹配关系,只促成距离相近的买卖双方之间达成交易。拍卖师在地理位置约束下确定可以进行交易的买卖匹配对,根据各个卖方提交的标的中的最大可服务距离以及所有参与拍卖的用户的位置坐标确定供需匹配关系。

若Dij表示买方i和卖方j之间的欧氏距离,当买卖双方之间的欧氏距离不超过λj时,卖方j可以为买方i提供电力资源,表达式如下

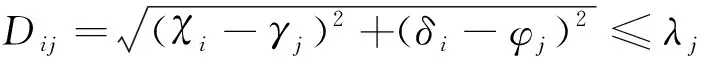
(1)

买卖双方之间的供需匹配关系用ηij表示,当卖方j可以为买方i提供电力资源时ηij=1,否则ηij=0。

1.3 电力资源分配方法及过程

本文所述的基于双向拍卖的电力资源分配包括确定中标者和确定价格两个阶段,其主要经济目标是在局部约束下实现社会效益最大化。为了解决智能电网中的电力资源再分配问题,本文需要确定包括买方和卖方在内的赢家集合,并确定获胜买方的支付价格和获胜卖方应得的报酬,同时保证真实性、个人理性以及预算平衡。

真实性:保证买方和卖方都进行真实的出价和要价,虚报价值不会带来任何优势。

个人理性:买方付款要低于自己的真实出价,卖方收入要高于自己的真实成本。

预算平衡:获胜买方的总支付价格应高于卖方的总收入,这样才能使得买方、卖方以及拍卖师都可以获得收益。

由于资源分配问题的最优解法是一个整数规划问题,整数规划问题已被证明是NP-hard(non-deterministic polynomial-time hard,NP难)问题,当问题规模较大时,无法在多项式时间复杂度下得到最优解。本文为了降低计算复杂度,将整数规划问题的限制条件松弛,将本文的智能电网电力资源再分配问题描述为一种线性规划问题LP(I,J)

(2)

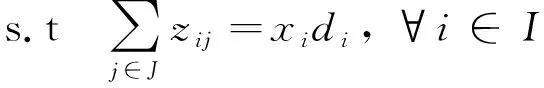
(3)

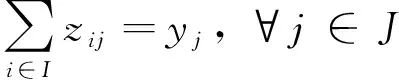
(4)

0≤zij≤sjηij, ∀i∈I, ∀j∈J

(5)

0≤xi≤1, ∀i∈I

(6)

0≤yj≤sj, ∀j∈J

(7)

式中:fSW(I,J)表示参与拍卖的买方用户集合为I,卖方用户集合为J时的社会效益;xi表示买方i的分配结果,若买方i得到自己所需的电力资源,则xi=1,否则xi=0;yj表示卖方j出售的电力资源单位数;zij表示买方i从卖方j处购买的电力资源单位数。约束式(3)确保所有买方的需求不可分割,即要么全部满足,要么全都不满足;约束式(4)表示每个卖方提供的资源数量;约束(5)表示只有当卖方j和买方i之间可以进行交易时,卖方j和买方i之间的交易才有效;约束式(6)表示xi的取值范围,约束式(7)表示yj的取值范围。

在使用拍卖作为资源分配的方法时,需要满足几种经济属性,其中最重要的经济属性就是真实性,其次是个人理性。本文采取双向拍卖方法,除了需要满足真实性和个人理性以外,还需要满足预算平衡。为此,本文采取文献 [31]中所提出的填充机制。填充机制就是通过在拍卖过程中引入一个预算不受限制的虚拟买方,有意地在卖方供给和买方需求之间制造不平衡。虚拟填充向量的使用增加了买方用户的总电力资源需求量,加剧了买卖双方之间的竞争,导致了更高的购买价格、更少的交易量和更低的销售价格,避免了潜在的不真实出价和要价行为,这有利于实现真实性、个人理性和预算平衡。本文设计的资源分配算法的伪代码中涉及到的变量符号包括:买方分配向量x,买方i的分配结果xi;卖方分配向量y,卖方j的分配结果yj;买方i和卖方j之间交易的电力资源单位zij;买方k的填充向量Qk;线性规划问题LP(I,J)的解(x′,y′,z′),一次获胜的买方用户集合I′;线性规划问题LP(I,J,Qk)的解(x″,y″,z″),二次获胜的买方用户集合I″;线性规划问题LP(I″,J)的解(x‴,y‴,z‴);资源分配问题的最终解(xfinal,yfinal,zfinal)。本文设计的资源分配算法的伪代码如下所示。

输入:m,n,I,J,Bi:i=1, 2, ,m,Aj:j=1, 2, ,n;

输出:(xfinal,yfinal,zfinal)

1 /*****确定供需匹配关系ηij*****/

2 初始化ηij、I′、I″、xfinal、yfinal、zfinal为0;

3 fori∈I

4 forj∈J

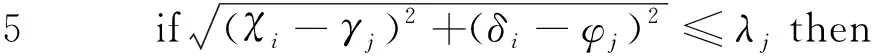
6ηij=1;

7 end

8 end

9 end

10/**********资源分配**********/

11解LP(I,J),获得解(x′,y′,z′)

12I′={i|x′i=1,i∈I};

13fork∈I′

15 解LP(I,J,Qk),获得解(x″,y″,z″);

16 ifx″k=1 then

17I″=I″∪{k};

18 end

19end

20解LP(I″,J),获得解(x‴,y‴,z‴);

21fori∈I″

23 forj∈J

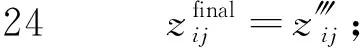
25 end

26end

27yfinal=y‴;

28return(xfinal,yfinal,zfinal)

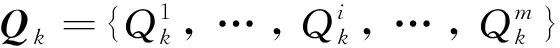
通过调用标准LP求解器求解LP(I,J,Qk),得到解(x″,y″,z″)(第15行)。线性规划问题LP(I,J,Qk)如式(8)所示

LP(I,J,Qk): maxfSW(I,J,Qk)=

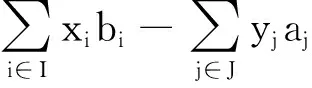
(8)

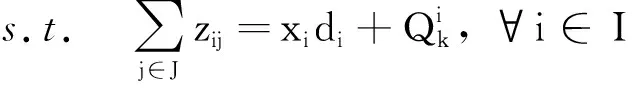
(9)

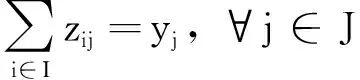
(10)

0≤zij≤sjηij, ∀i∈I, ∀j∈J

(11)

0≤xi≤1, ∀i∈I

(12)

0≤yj≤sj, ∀j∈J

(13)

式中:fSW(I,J,Qk)表示参与拍卖的买方用户集合为I、卖方用户集合为J、填充向量为Qk时的社会效益。如果x″k=1,则用户k为获胜买方,将其添加到买方赢家集合I″中(第16～18行);最终,通过调用标准LP求解器求解LP(I″,J),得到解(x‴,y‴,z‴),并据此得到最终分配结果(xfinal,yfinal,zfinal)(第20～27行)。

1.4 定价策略

在保证真实性、预算平衡和个人理性的前提下,本文分别采用基于关键值的定价策略和基于VCG的定价策略来确定获胜买方用户的支付价格和获胜卖方用户应得的报酬。这里的VCG机制是指无策略的Vickrey-Clarke-Groves定价机制[32]。VCG机制能够在激励相容的约束条件下,使参与博弈的人主动披露自己的信息,进行真实报价,除此之外,根据收益等价原理可知,凡是满足真实性和个人理性的机制,其计算得到的所得报酬一定小于VCG机制得到的所得报酬。因此,在所有满足个人理性和真实性的机制之中,VCG机制能够实现卖方用户利益的最大化。本文采用VCG机制确定获胜卖方用户应得的报酬,能够实现经济效益、真实性与个人理性。关键值定价策略可以保证买方用户以最低的支付价格获得自己所需的电力资源,从而实现经济效益以及个人理性。通过基于关键值的定价策略确定买方用户的最低支付价格,基于VCG机制的定价策略确定卖方用户的最高所得报酬,可以在满足真实性以及个人理性的同时帮助实现社会效益最大化。

(14)

本文设计的关键值定价算法的伪代码如下。

输入:Bi:i=1, 2, ,m,Aj:j=1, 2, ,n,Qi:i∈I″,I″;

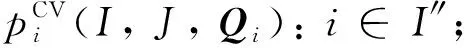
1 fori∈I″

2bl=0;

3bu=bi;

4 while (bu-bl)≥1 do

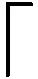
6Bi=(di,bmid, (χi,δi));

7 解LP(I,J,Qi),获得解(x″,y″,z″);

8 ifx″i=1 then

9bu=bmid;

10 ifbl=bu-1 then

12 break

13 end

14 else

15bl=bmid;

16 ifbl=bu-1 then

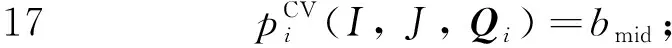
18 break

19 end

20 end

21 end

22end

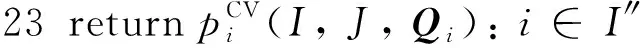
本文采用二分搜索法获得每个获胜买方用户的关键价格。首先,对每一位获胜的买方用户i∈I″,初始化其关键价格的上界bu和下界bl(第1～3行);更新用户i的投标价格为bmid,解线性规划问题LP(I,J,Qi),得到用户i的解x″i(第5～7行),若x″i=1,则更新当前投标价格为上界(第8～13行),若否,则更新当前投标价格为下界(第14～20行);最终得到用户i的关键价格作为其最终付款价格(第23行)。

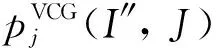
fSW(I″,J{j}))

(15)

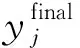
2 实验结果与讨论

2.1 实验方案

在一个面积为500 m×500 m的应用区域进行了应用测试实验,在场景中部署了50个出售富裕电力的卖方和200需要购买电力资源的买方。每个买方的单位投标价格随机均匀分布在 [1, 2]元的范围内,买方请求的电力资源单位在 [300, 500]kW·h范围内随机均匀分布。同样,每个卖方出售其电力资源的单位要价在 [0, 1]元范围内随机均匀分布,而每个卖方提供的电力资源单位在 [500, 1 600]kW·h以内。卖方所出售电力资源的最大传输半径是在 [100, 500]m内随机均匀生成的。LP求解器使用Java平台的ILOG CPLEX12.10.1。在Java平台上使用ILOG CPLEX 能够求解最大化社会福利问题的最优解。

2.2 性能评价

鉴于智能电网背景下暂时没有使用基于双向拍卖进行电力资源分配的相关研究,本文选用一种移动边缘计算环境下的基于双向拍卖进行计算资源分配论文中的基于盈亏平衡的双向拍卖(breakeven-based double auction,BDA)方法[33]和最优资源分配方法作为对比方法,与本文提出的基于线性规划的填充分配方法进行性能比较。关于BDA的详细介绍可以参考文献[33],而最优资源分配方法是直接解决社会福利最大化问题的一种简单方法,最优资源分配方法中的付款价格和报酬均采用第一价格定价策略,即如果某个买方获胜,他直接支付其投标价格,而获胜的卖方获得的报酬等于其声称的成本乘以提供的资源数量。本文通过与最优分配机制的结果进行比较,找出本文提出的基于线性规划的填充分配方法与最优解之间的差距。

为了检验性能,本文采用了3个评估指标,这些指标可以反映算法的不同性能属性。这些指标包括:①社会效益(元),衡量拍卖效率的指标,即所有参与者的效益总和,在本文表示为所有买方的投标价格之和与所有卖方的投标价格之和的差;②资源利用率,所有获胜卖方成功出售的富裕电力资源量与所有卖方待出售的富裕电力资源总量的比值;③时间开销(s),资源分配机制算法的运行时间,需分别进行计算和评估。

在此实验中,考虑一个电力资源分配场景,其中卖方的数量固定为50,而买方的数量从100到200不等。社会效益、资源利用率和时间开销的对比结果分别如图2～4所示。

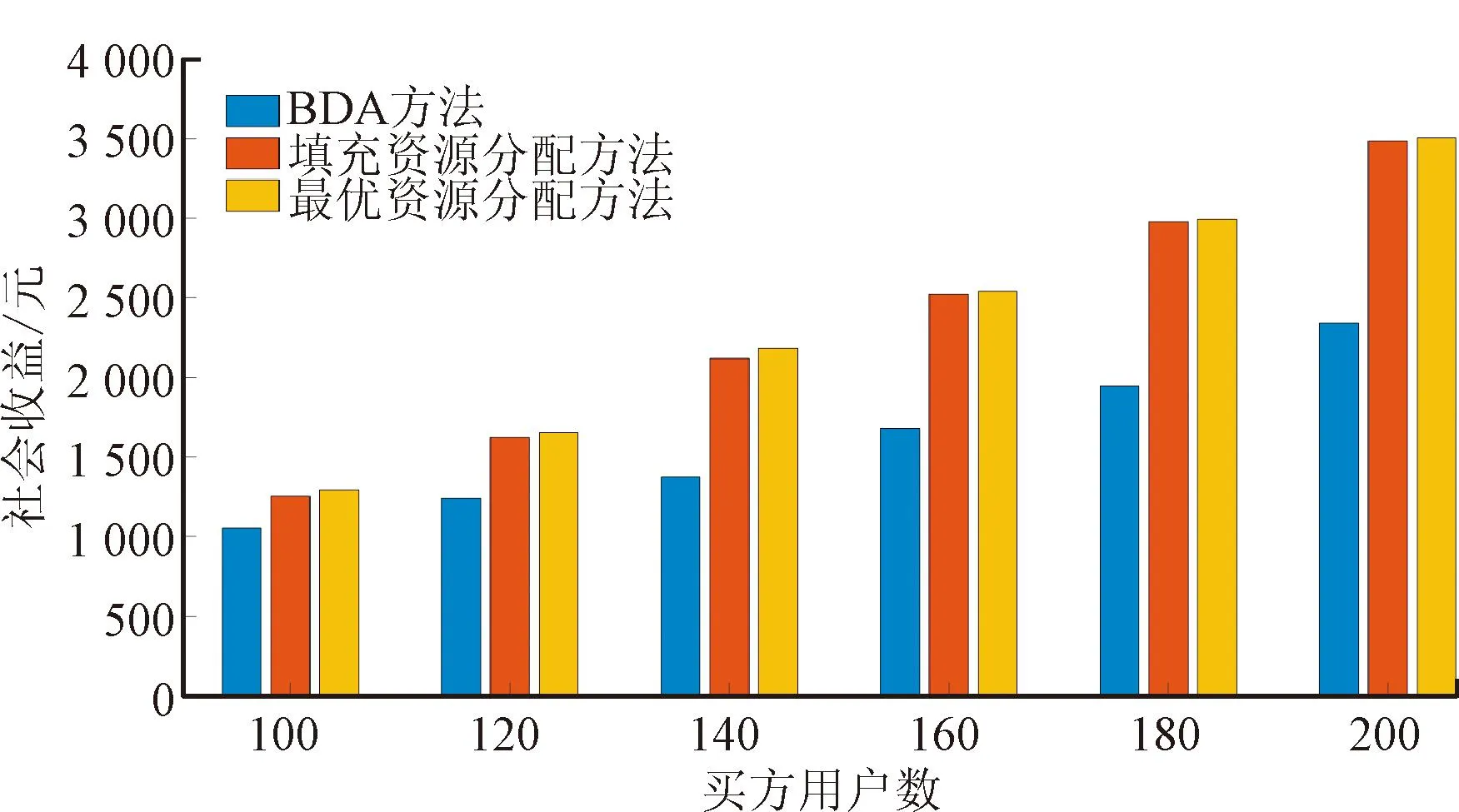
图2 社会效益随参与拍卖的买方用户数量变化对比Fig.2 Comparison of social benefit with the number of buyers participating in the auction

从图2可以看出,本文提出的基于线性规划的填充分配方法相对于BDA方法具有明显的优势,基于线性规划的填充分配方法实现的社会效益始终高于BDA方法,同时随着买方用户数量的增加,这种性能差距更加明显。这是因为基于线性规划的填充分配方法的组合资源供给更灵活,在电力资源分配过程中更倾向于选择更有益的交易。由于最优资源分配方法以最优的方式解决了社会效益最大化问题,所以它在所有机制中能够产生最高的社会效益。

从图3可以看出,随着买方用户数量的增加,各机制中的资源利用率都呈上升趋势。与BDA方法相比,基于线性规划的填充分配方法在分配过程中可以产生更高的资源利用率。

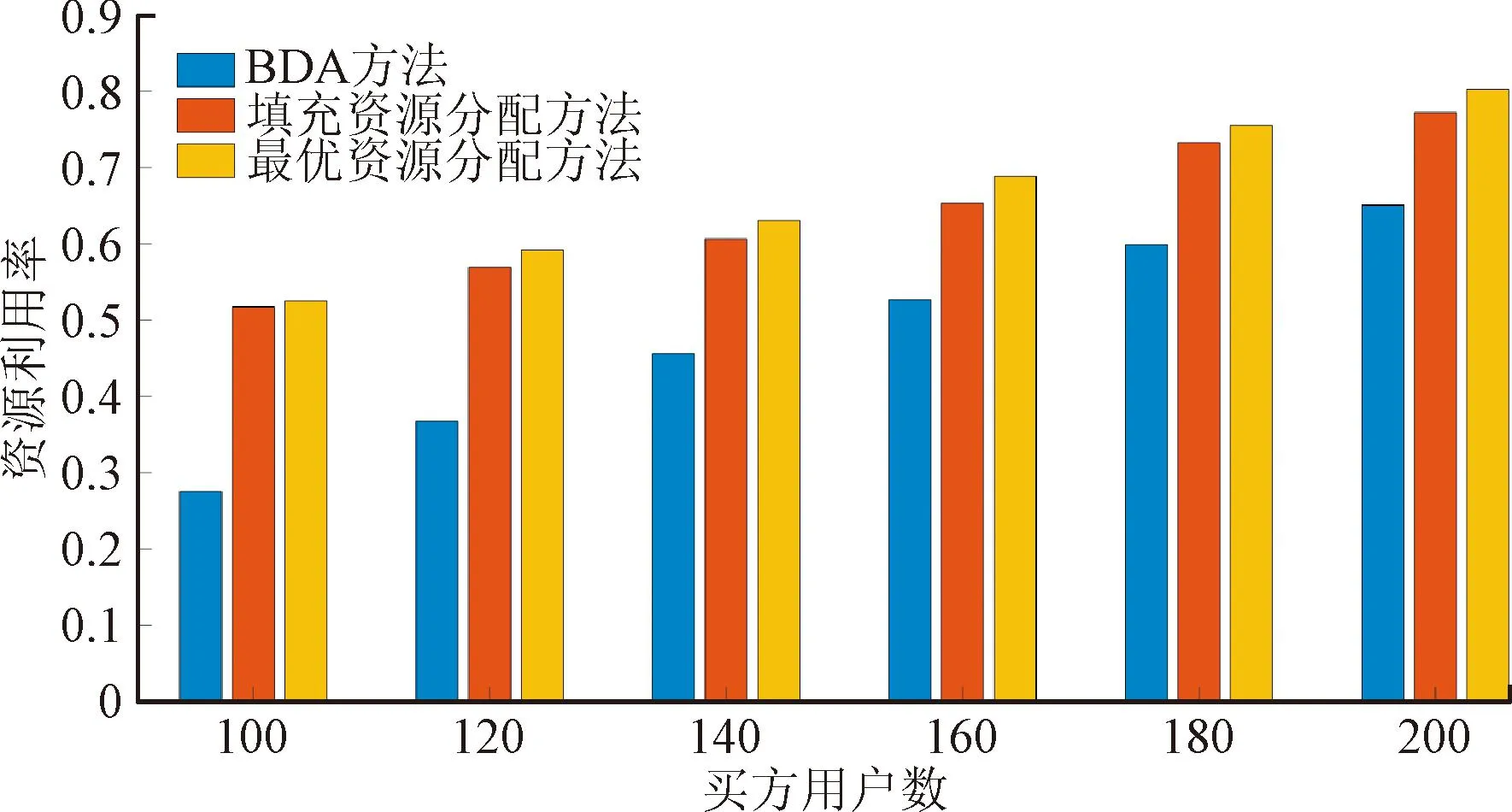
图3 资源利用率随参与拍卖的买方用户数量变化对比Fig.3 Comparison of resource utilization with the number of buyers participating in the auction

从图4可以看出,基于线性规划的填充分配方法的运行时间随着参与拍卖的买方用户数量的增加而逐渐增长。但是,运行时间的增长率与问题规模的关系不是指数级的,这说明本文设计的算法是可以在多项式时间内解决的。此外,可以看出基于线性规划的填充分配方法比BDA方法需要更多的时间开销。以时间开销为代价,基于线性规划的填充分配方法以其真实性和预算平衡性获得了更多的社会福利,虽然BDA方法运行开销较低,但没有表现出基于线性规划的填充分配方法的优势。

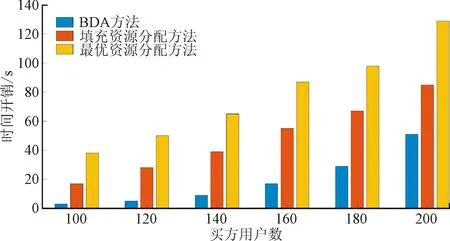
图4 时间开销随参与拍卖的买方用户数量变化对比Fig.4 Comparison of time expenditure with the number of buyer users participating in the auction

本文设计的基于线性规划的填充分配方法在社会效益和资源利用率方面都优于BDA方法,接近于最优资源分配方法给出的最优社会效益和资源利用率,且时间开销低于最优资源分配方法,在综合性能上具有有益效果。

2.3 属性验证

2.3.1 个人理性

为了验证基于线性规划的填充分配方法满足个人理性,本文通过某次参与拍卖的买方数量为400、卖方数量为100时的分配结果,给出获胜买方的支付价格和投标价格对比,如图5所示,其中绿色虚线是由买方投标价格形成的基准线。图6为中标卖方的报酬和要价对比结果,其中绿色虚线是由卖方要价形成的基准线。可以看出,每个获胜买方的支付价格均不超过投标价格基准线,每个中标卖方得到的报酬均不低于卖方要价基准线。因此,基于线性规划的填充分配方法是满足个人理性的。这些结果还表明,所有买方和卖方都具有非负效益。一方面,获胜的卖方获得到足够的奖励,从而激励他们出售富裕的电力资源。另一方面,获胜的买方获得所需的电力资源,并且其支付价格不超过对获得电力资源的估值。

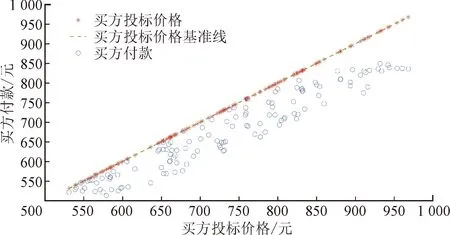
图5 获胜买方的付款和投标价格Fig.5 Payments and bidding prices of winning buyers

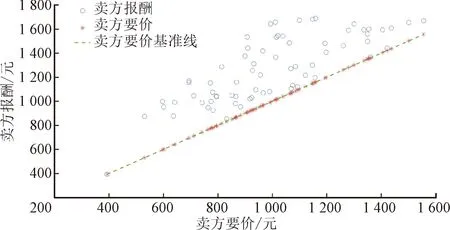
图6 获胜卖方的报酬和要价Fig.6 Rewards and asking prices of winning sellers

2.3.2 预算平衡

为了验证本文设计的基于线性规划的填充分配方法满足预算平衡,本文将获胜买方的总支付价格与获胜卖方的总报酬进行比较,如图7所示。其中,参与拍卖的买方数量固定为200个,参与拍卖的卖方数量固定从10到100逐步增加。从图7可以看出,获胜买方的总支付价格总是高于获胜卖方获得到的总报酬。因此,地方供电局愿意通过组织拍卖来获取非负效益。

图7 买方付款和卖方报酬的比较Fig.7 Comparison of payments of buyers and rewards of sellers

2.3.3 真实性

为了验证本文设计的基于线性规划的填充分配方法的真实性,随机选择两个买方和两个卖方,观察其效益如何随出价和要价的变化而变化,仿真结果如图8～11所示。

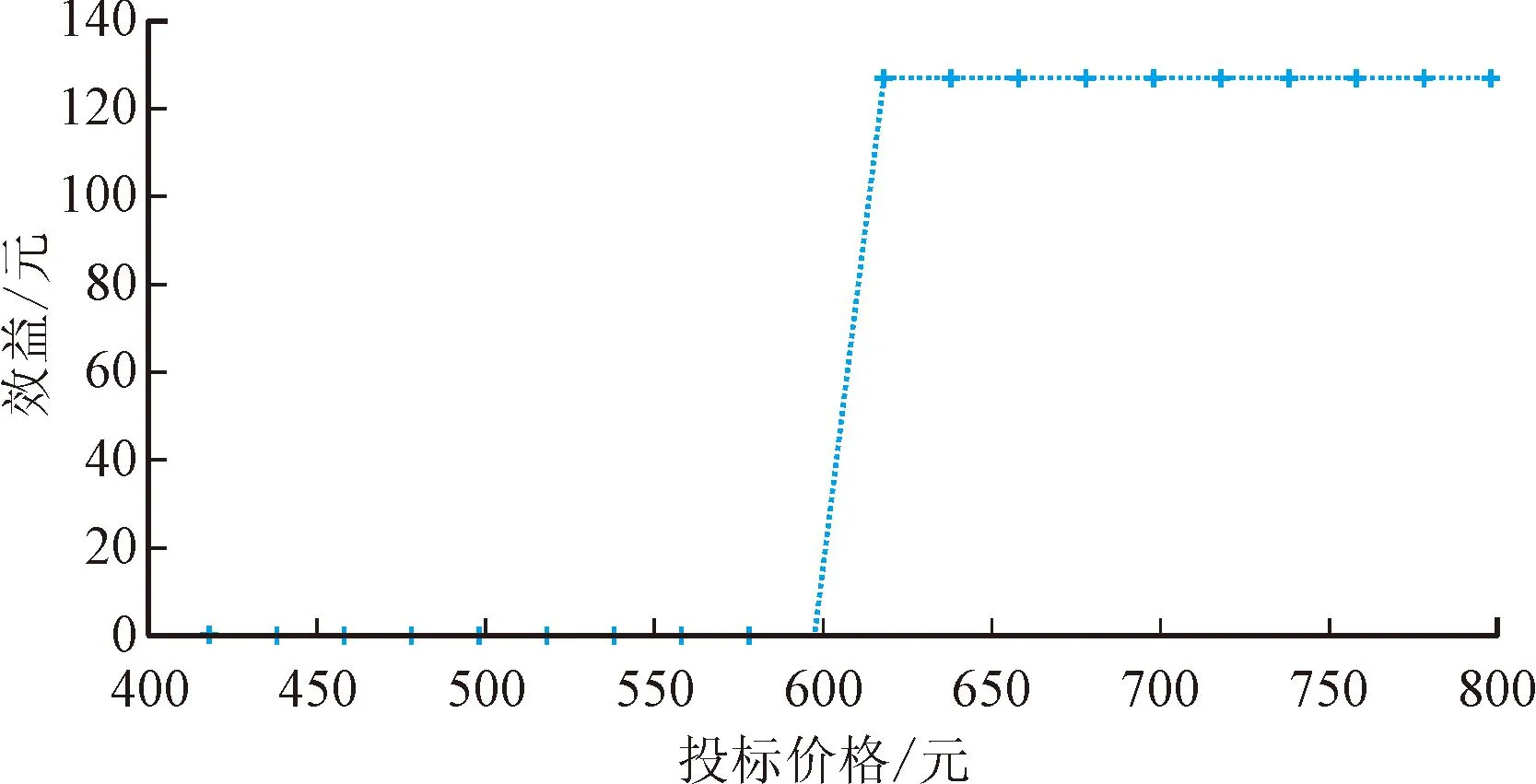
图8 买方i的真实性Fig.8 Truthfulness of buyer i

从图8可以看出,如果买方i以745元的真实价格投标,则可以获胜,并获得其效益127元。可以发现,无论如何改变出价,买方i都不能增加其效益。图9表明,如果买方i′以389元的真实价格如实投标,则无法获胜,即效益为0,即使通过不真实出价获得胜利,买方i′的效益也不会大于0。图10表明,如果一个卖方j以真实价值0.6元作为要价进行投标,则他可以中标并获得效益173元。从图中还可以观察到,当卖方j在竞标中进行真实要价时,可以获得最高的效益。图11显示,如果卖方j′以真实价值0.8元作为要价进行投标,则他在此次拍卖中会失败,效益为0,即使他通过使用不真实的要价请求中标,其效益也不会大于0。从上述结果中,可以观察到本文设计的基于线性规划的填充分配方法对所有参与拍卖的买方和卖方都是真实的,因为他们的效益不能通过不真实的出价或要价来增加。

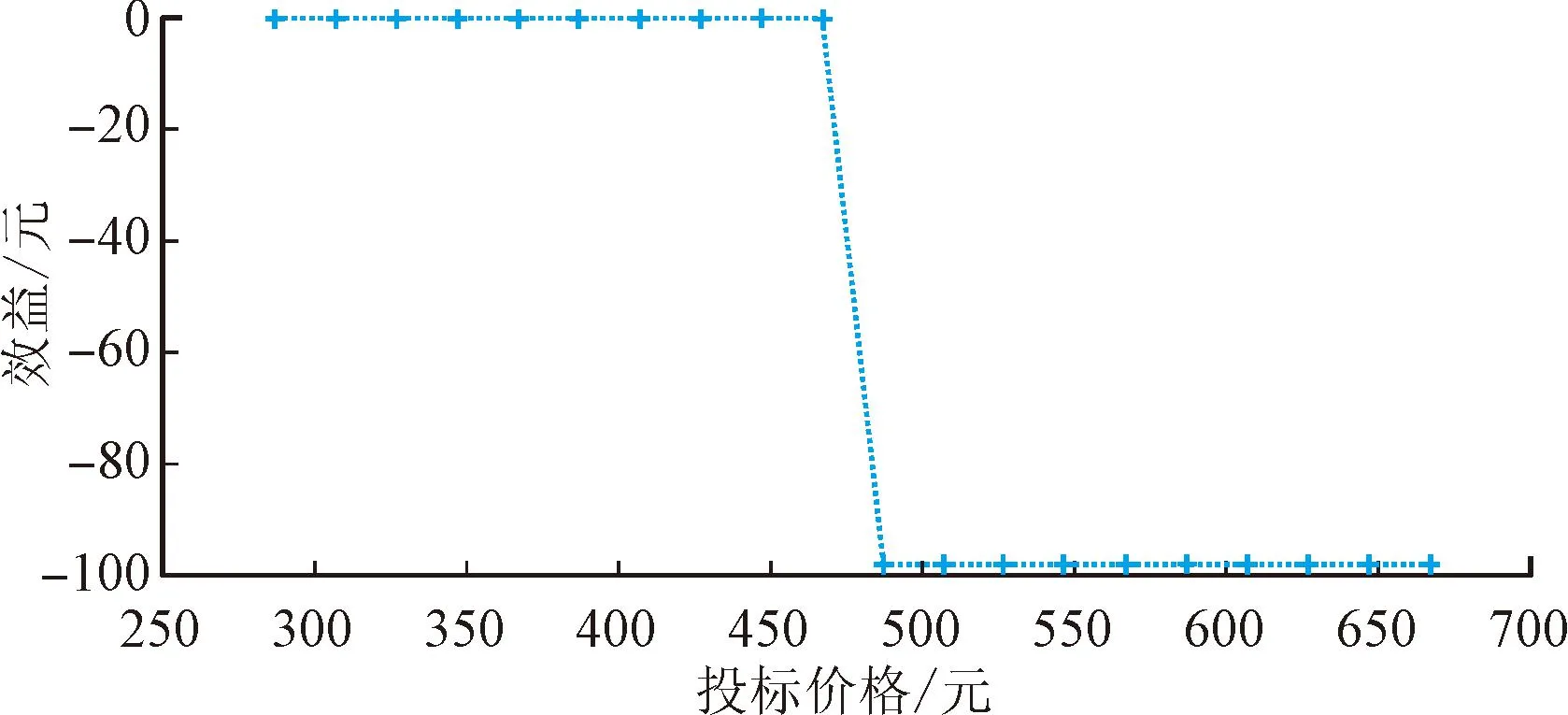
图9 买方i′的真实性Fig.9 Truthfulness of buyer i′

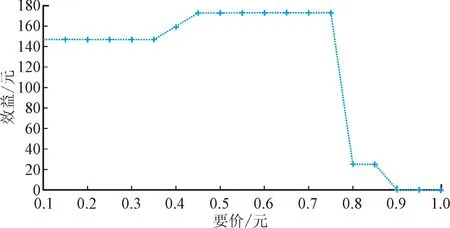
图10 卖方j的真实性Fig.10 Truthfulness of seller j

图11 卖方j′的真实性Fig.11 Truthfulness of seller j′

3 结 论

随着互联网技术的迅速发展,智能电网逐渐普及,互动电网的概念被提出。互动电网可以推进电网消费者之间以及消费者和电网管理者之间的大规模互动。用户的富裕电力回售是互动电网中亟需解决的问题之一,实现富裕电力回售可以有效解决局部区域电力资源过剩而局部区域电力资源短缺的问题。但是,相较于电力资源的一次分配,富裕电力回售涉及电力资源的再分配,出售富裕电力的用户不愿意亏本出售电力资源,而电力紧缺的用户也不愿意以高于购买电力所带来价值的价格购买电力资源,且地方供电局需要作为中间人完成消费者之间的电力资源再分配,因此需要设计一种合理的交易规则和定价机制激励消费者和地方供电局完成电力资源的再分配。

针对此问题,本文提出了一种具有动态定价策略的真实双向拍卖机制,用于实现智能电网环境下的电力资源再分配。在本文中,考虑了买卖双方的地理位置信息,通过确定供需匹配关系减少电力传输过程中的损耗;采用了基于线性规划的填充分配方法,保证了智能电网环境下电力资源再分配过程中局部约束下的理想真实性,并且在多项式时间内获得近似最优解的分配结果,通过将虚拟填充用户引入到买方用户集合中,故意造成供应可用性与需求之间的不平衡,从而保证了双向拍卖下的预算平衡;针对买卖双方分别采用了基于关键值的定价策略和基于VCG机制的定价策略,保证了买卖双方在拍卖中的真实性以及个人理性;通过仿真实验证明了基于线性规划的填充分配方法满足个人理性、预算平衡和真实性,仿真结果验证了本文设计的智能电网环境下的电力资源再分配方法以及定价策略的有效性。

然而,本文注意到,在极端情况下,当卖方用户很少(例如只有一个卖方用户)时,本文设计的填充机制可能不会有效地增加社会效益,因为仅有的卖方可能会与虚拟填充用户进行交易,而不是与真实用户进行交易,这可能会降低社会效益。因此,在未来的工作中,可以关注虚拟填充用户的设计,以增强处理各种情况的通用性。此外,还可以研究如何提高算法对更大规模的智能电网电力资源再分配业务场景的适用性。