改进的局部最值分段多项式拟合算法精确校正拉曼光谱基线

田超凡, 李剑君, 翁国军, 朱 键, 赵军武

西安交通大学生命科学与技术学院, 教育部生物医学信息工程重点实验室, 陕西 西安 710049

引 言

拉曼光谱(Raman spectrometry)为散射光谱, 能够反映分子内部的振动与转动能级, 拉曼光谱分析技术是根据光谱的频率、 强度和偏振等信息去获取样品的特征, 因此, 不会破坏检测物和制备检测样品, 以其快速、 简单、 可重复、 无损伤和信息丰富等优点广泛应用于各类物质成分分析以及对各种不同材料特性的探索[1]。 例如用来诊断肿瘤组织、 分析食品中的营养成分常会考虑到拉曼光谱分析技术的无损特性[2]。 然而, 在拉曼光谱信号获取过程中, 一些物理效应及干扰物会影响生物样品和成分的拉曼光谱[3]。 尤其一些生物组织样品会在拉曼检测中呈现高自发荧光背景的拉曼信号, 干扰拉曼光谱的准确识别, 甚至极大可能埋没样品的光谱信息[4]。 因此, 拉曼光谱分析中的预处理步骤, 例如抑制背景噪声、 校正基线, 能够消除光谱中荧光和其他附加特征的影响[5], 对光谱的定性定量分析起重要作用。

现阶段为抑制背景噪声, 常用的实验手段和数字处理这两种方法。 实验手段通常操作成本较高, 操作流程复杂, 因此推广难度较大。 相比而言, 数字处理法所需成本低, 且操作简便快捷, 因而具有出色的应用潜力。 数字处理方法包括频域滤波、 小波变换和曲线拟合等[6-8]。 频域滤波参数设计复杂。 小波变换计算量和计算复杂度相对较高, 因而曲线拟合应用较为广泛和普遍, 本课题组曾提出了一种基于自动线性拟合的快速拉曼基线校正算法(FR-BCA)来解决类似缺陷, 其核心思想就是从原始光谱中寻找一系列标记点将光谱分段并循环线性拟合直至得到最合适的基线。 这与Chen等[9]基于迭代平均形态打开和关闭操作的自适应和全自动基线估计算法所提出的方法相似, 都能够处理基线的不同形状和幅度。 B-spline曲线具有低阶和平滑的优点, Wang等[10]将其作为拟合算法, 有效避免欠拟合和过拟合且不需要用户输入, 简化了操作。 Liu等[11]结合谱峰识别算法和自适应重复加窗去除峰值操作, 完成拉曼光谱的基线拟合; 使用传统多项式曲线拟合算法[12-13]的方式进行基线校正也已经广泛进行了讨论和研究, 但是仍存在一些问题和挑战, 例如拟合阶数难以确定, 不同拉曼光谱拟合基线的分段窗口大小难以选取, 针对选取背景点仍采用人工的方式, 依赖性太强。 因此在不增加实验设备成本的前提下, 针对传统基线校正-分段多项式拟合(piecewise polynomial fitting, PPF)的方法进行了改进, 提出局部最值分段多项式拟合(numlocal piecewise polynomial fitting, NPPF)算法。 针对拉曼光谱窄峰、 对称的特点改进了局部最值背景点选取的方式, 克服了选取背景点对人工的依赖性。 同时又改进分段多项式曲线拟合方法, 解决了曲线拟合阶数和分段窗口难以确定的难题, 而且具备保留弱拉曼峰段, 防止过拟合和欠拟合的优点。 先模拟带有不同类型和信号强度背景的拉曼光谱, 并使用NPPF和PPF对模拟的光谱分别进行基线校正, 再对实际样品中带有基线漂移的拉曼光谱分别进行两种算法验证, 证实了NPPF较于PPF能更有效地消除拉曼光谱的基线漂移, 为进一步拉曼光谱数据的分析和实现拉曼光谱成像提供准确可靠的信息。

1 算法原理

1.1 基于自适应窗口局部最值的背景点选取

常见各类曲线拟合方式均建立在已选取的背景数据点的基础上, 背景点的选取对于后续基线拟合具有关键意义, 传统方法多采用人为预选取基线数据点, 再在其前后三点中取最小值作为目标点。 人工背景点的选取过于依赖经验且操作繁琐。 也有采用多次迭代的多项式方法[14]进行初始基线估计作为基线背景代替人工选取方式, 然而此类方法计算量大且易造成基线点偏差, 出现过校正或拟合不充分现象。 另外有使用直接比较法选取波谷作为背景点的方式, 但是无法有效确定比较的窗口, 较大噪声可能使选取的背景点不在底部背景轮廓上, 同样会出现拟合不准确的现象。 本工作在选取背景点方面进行了改进。 选择了两种拉曼光谱常见的基线漂移方向左上漂移、 右上漂移, 用以讨论背景点选取时窗口宽度W的确定方式。 如图1所示(a)、 (b)选取W长度作为整体移动的窗口大小, W应选择在最宽峰的底部, 近似为峰宽, 每个W内找寻最小值两个点作为背景点, 这样W的宽度保证能涵盖所有不连续的拐点, 同时保证所有选取的背景点都在底部背景轮廓上。 移动窗口选取不同的背景点放入序列f(x), 再进行下一步的曲线拟合。

图1 窗口宽度W的选取方式

1.2 改进的迭代多项式曲线拟合

PPF从光谱中选取拟合背景数据点序列f(x), 通过定义合适的拟合阶数和寻找合适的分段窗口[15], 根据最小二乘原理计算出满足通过f(x)的最佳逼近函数。 在此过程中, 不同基线对应拟合的多项式阶数不同, 窗口大小也不同。 如果选取阶数过高, 拟合曲线的上下震荡范围比较大, 甚至会出现Runge现象, 且计算量大; 而阶数过低, 拟合不够充分, 误差大, 会掩盖较弱拉曼峰段。 PPF对复杂高噪声的拉曼光谱也难以有效处理, 确认处理的最优窗口大小也是其面临的重要困难之一。

本工作对PPF进行了改进, 首先在选取窗口大小上设置为图1中的W。 为了保证曲线拟合的契合度, 需要使得所选多项式函数曲线有较好的波动走向, 可选取多项式阶数为奇数, 同时为了算法在计算过程中的简洁快速, NPPF的多项式曲线拟合最终使用3阶多项式, 并且每次选取5个背景点。 每一个窗口内都模拟出三个前(Ff)、 中(F)、 后(Fa)的3次多项式函数进行迭代覆盖; 例如分段拟合中: 目标为拟合出x值在30～50范围之间的y值, 第一步: 先拟合三种曲线x值范围分别为[20, 40]、 [30, 50]、 [40, 60]的三条对应3阶多项式曲线函数Ff、F、Fa, 第二步: 计算三条曲线对应函数的区间[30, 50]的函数y1,y2,y3, 第三步: 计算y1,y2,y3与上一个拟合点y0的差值绝对值, 选择绝对值最小的设为拟合的基线值; 而基线最初点设为原始光谱的起点y值。 因此这样迭代覆盖的方式使得基线不会出现较大的震荡与波动。 这种在三次模拟基础上取最小绝对值的方法可以有效防止多项式拟合出现过拟合和欠拟合的值。 整体算法流程如图2。

图2 NPPF算法流程

2 结果与讨论

2.1 模拟数据

为验证本算法的有效性和可行性, 验证的数据由matlab2021b进行模拟。 根据拉曼谱峰的特点, 在数据模拟中随机引入了高斯峰型[图3(a、 d、 g)]、 洛伦兹峰型及混合峰型[图3(j)]作为拉曼光谱特征峰的模拟峰型; 同时为了模拟常见的两种基线漂移类型(左上漂移、 右上漂移), 选择对应的模拟指数型(e)函数曲线和反曲线(f)型曲线作为理想光谱的基线背景。 分别模拟四组数据如图3所示。

图3 四组模拟的理想及引入曲线背景的拉曼光谱

图3中, 每组拉曼光谱数据引入两种不同类型基线背景: 指数型(e)基线和反曲线型(f)基线背景。 特别是, 第三组(g)加大了基线背景信号强度与拉曼特征峰强度的比值, 模拟出高荧光背景下弱拉曼峰的光谱情形(h、 i); 而在第四组(j)则模拟了带有洛伦兹峰型、 高斯峰型、 多项式曲线峰型及混合峰型的拉曼光谱(k、 l)。

2.2 模拟光谱基线校正结果对比验证

PPF实现所需的参数主要有两个: 分段的窗口大小P, 拟合阶数R; NPPF只需要确定一个参数窗口宽度W; 为了保证对比的有效性, 两种算法均选取了最优参数进行验证, 其中通过式(1)循环取优计算选取最优阶数和窗口作为PPF参数, NPPF的窗口参数采用1.1中讨论的方式选取, 具体参数见表1。

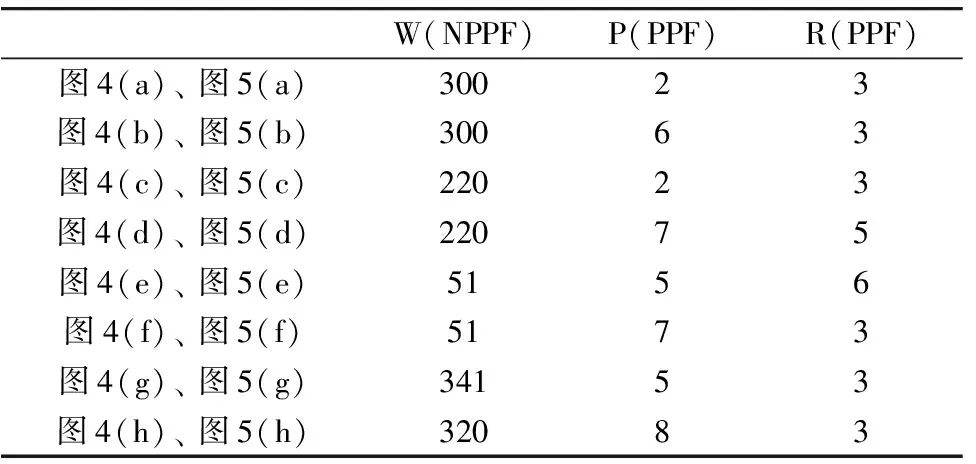
表1 PPF与NPPF算法处理所选取的参数数值

在选取好参数后, 对2.1中模拟的光谱数据进行处理得到基线如图4所示, 其中红色代表NPPF模拟的基线, 蓝色代表PPF模拟的基线。

图4 PPF与NPPF基线拟合效果对比

从图4中可以直观地看出NPPF模拟的基线(红色)普遍比PPF(蓝色)拟合的基线更准确地包络拉曼光谱。 在PPF的处理下, 图4(a)在600～1 000和1 350 cm-1附近其拟合的基线(蓝色)存在一定程度的过拟合, 在起始处(400 cm-1)则存在欠拟合现象; 图4(b)中在500～1 000 cm-1出现过度拟合, 而在1 550 cm-1附近出现了欠拟合。 图4(c)、 (e)、 (g)中PPF模拟的基线则不能很准确地包络背景轮廓, 使得背景的去除不彻底, 基线校正不准确。 与之对比, NPPF在以上情况下处理得到的基线则更准确, NPPF处理的过拟合和欠拟合程度均远低于PPF。

图5显示了PPF和NPPF处理后扣除基线后的拉曼光谱, 并对比图4观察得出, NPPF基线校正后的拉曼光谱(红虚线)与理想光谱(黑实线)重合度明显高于PPF基线校正后的拉曼光谱(蓝色虚线)与理想光谱的重合度。 在图4(e)、 图4(f)和图5(e)、 图5(f)对比显示了对于高背景信号强度基线的处理结果。 图4(e)中显示PPF并未准确的实现背景轮廓的包络, 而使得背景基线去除不彻底, 因此在图5(e)中可以看出扣除基线后的校正拉曼光谱仍然存在一定程度的基线漂移; 同样, 在图4(f)中PPF对起始拉曼位移(400 cm-1)附近拟合不充分也使得在图5(f)中对应的基线校正结果相同位置出现误差。 然而, 与之对比NPPF处理结果则没有上述现象。 从整体来看, NPPF的算法效果优于PPF。 在第四组数据的处理结果中, 图4(g)显示的NPPF的拟合基线包络性更好, 图5(g)、 (h)也显示出NPPF处理后的校正拉曼光谱与理想光谱之间重合度较PPF更好, 也验证了NPPF针对复杂拉曼光谱仍有良好的处理效果。

图5 PPF与NPPF基线校正结果对比

为了进一步确认与验证基线拟合的效果, 将拟合后的基线扣除得到的拉曼光谱与理想光谱做误差计算, 采用均方根误差(root mean square error, RMSE)的评价指标计算处理过后的光谱的误差大小。 设标准理想光谱为P(x), 基线校正后的光谱为P′(x), 则有如式(1)

(1)

式(1)中,S为光谱数据的长度或光谱采样数据点数; 本研究中S=3 112。x序列对应光谱拉曼位移横坐标的个数,P为纵坐标强度。 RMSE的值越小, 代表与理想光谱越是接近即基线拟合的效果越好, 即证明NPPF算法的优越性越高。 结果如图6(a, b)。

图6 带有e型(a)和f型(b)背景基线的拉曼光谱通过PPF(蓝)和NPPF(红)处理的RMSE结果

由图6中可以得知, 无论是针对e型曲线背景还是f型曲线背景, NPPF算法处理的结果误差均小于PPF算法处理的结果误差, 证实NPPF相比PPF具有较大的优越性。

2.3 实际光谱测试

为进一步检验本基线校正方法的实际应用效果, 采用拉曼光谱仪(激光波长633 nm, 功率20 mW, 光谱范围400～2 000 cm-1)对样品烯啶虫胺、 罗丹明6G进行了拉曼光谱检测。 分别使用NPPF和PPF算法对两种实际拉曼光谱进行基线的拟合, 结果如图7(a, b)所示。

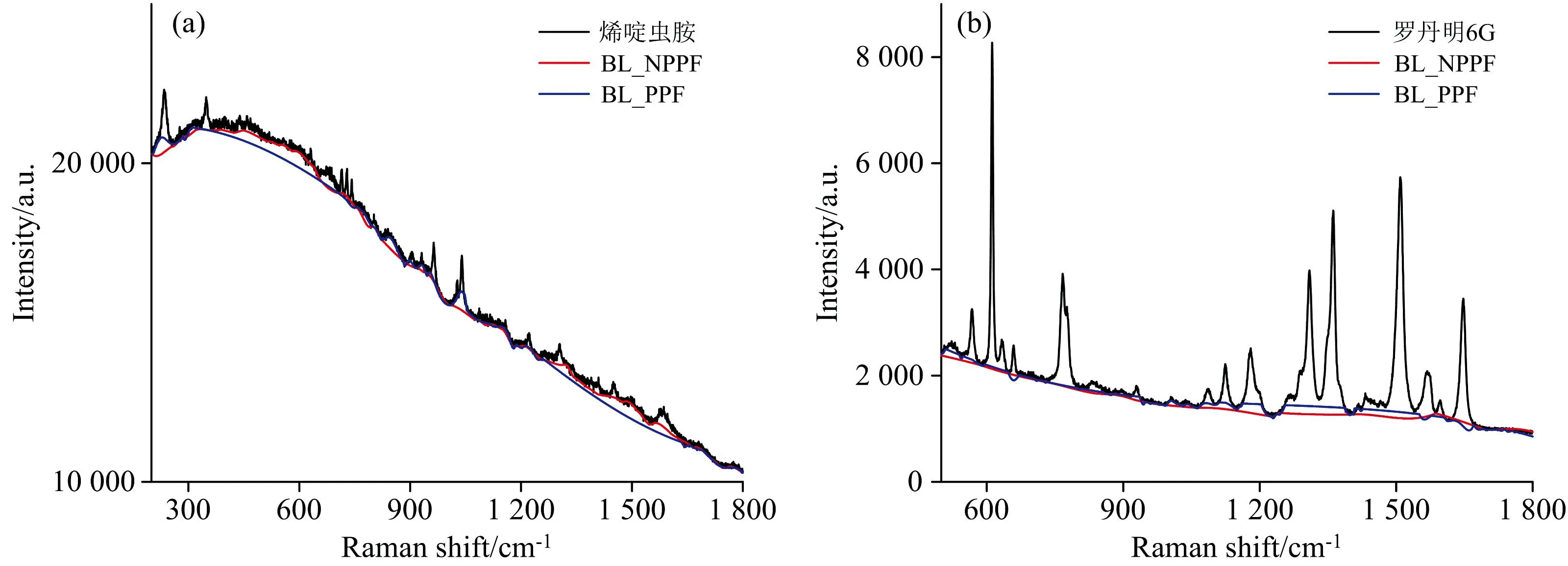
图7 烯啶虫胺(a)、 罗丹明6G(b)拉曼光谱及基线拟合结果

图7中观察PPF(蓝色)和NPPF(红色)基线拟合结果可知, NPPF算法能够较好地实现背景轮廓的包络, PPF则在图7(a)的300～600和1 200～1 500 cm-1附近拟合不够充分, 在200和1 000 cm-1附近出现过拟合现象, 而与之对比的NPPF则未出现此种现象。 类似地, 观察图7(b)的PPF处理结果(蓝色)可知1 100 cm-1附近及1 350 cm-1附近出现了过拟合, 而在650 cm-1附近和1 650 cm-1附近出现欠拟合的现象, 而对应NPPF则没有这种现象。 通过对实际样品拉曼光谱的算法验证, 证明了NPPF算法的实际应用效果优于PPF。

3 结 论

提出了一种基于局部最值改进的多项式校正拉曼光谱基线的方法, 利用分段局部最值算法识别背景点数据, 通过优化多项式分段拟合时的覆盖方式, 从而最大程度上减少了拟合过程中的过拟合和欠拟合现象, 实现对拉曼光谱信号的基线校正。 与传统多项式拟合基线相比, 本算法克服了分段时窗口难以确定, 阶数选择困难的缺点, 拟合的整体和局部基线准确性均较好, 通用性强, 适用范围广。 对于背景信号强度较大而拉曼特征峰较弱的光谱信号以及带有各种不同种类复杂峰型的拉曼光谱, 本算法均表现出较好的校正效果。 因此本算法有望作为一种有效、 简洁的基线校正方法广泛应用到实际中。 另外在本算法中, 多项式阶数和背景点数固定, 未来在不考虑算法复杂度和计算量的情况下, 可以改变阶数和背景点数的选取数量, 以进一步探究基线校正的结果是否得到更大的优化; 同时考虑局部最值背景选取算法的原理, 未来也将测试NPPF在其他光谱基线校正的使用效果。