深度学习探本质 整体架构育素养
——分数乘法单元整体教学的实践与思考
2024-04-08江苏省常熟市世茂实验小学杨佳玲
江苏省常熟市世茂实验小学 杨佳玲
《义务教育数学课程标准(2022年版)》强调,课程内容的组织重点是对内容进行结构化整合,探索发展学生核心素养的路径。结构化是数学学科的突出特点,任何一个数学知识点都不是孤立的,而是存在于整个知识系统中,各个知识点与它的核心概念、与其他知识点之间存在着某种逻辑关联,从而形成网状的知识结构。而单元整体教学是一种注重整体关联、迁移理解、深度探究与多元融合的教学模式,它所聚焦的核心内容在思维方式和学习方式上具有统一性。因此,进行单元整体教学有利于学生在结构化的数学学习中实现自主迁移和深度理解,培养思维、提升素养。
下面以苏教版数学六年级上册“分数乘法”单元的教学为例,基于深度学习理念,从结构化视角对单元知识进行再审视、再研读,对单元知识的教与学进行再思考、再实践。
一、深度分析学情,锚定学习起点
为了了解学生的认知起点,精准定位教学目标,有效组织教学,促进深度学习的真正发生,笔者课前从分数乘法算法的掌握程度、算理的理解程度两个方面对学生进行了学情前测和访谈,具体内容见图1。

图1
学情前测中两道题的正确率都达到了80%以上,大部分学生已经通过自学或预习了解并掌握了分数乘法的计算方法——分母乘分母,分子乘分子。其中小部分学生能主动联系乘法的运算意义将“×3”转化为“”进行计算并说理;个别学生将“”转化为“0.75×0.5”并能说明自己的计算结果是正确的;但几乎没有学生想到用画图来说理。访谈中被问及为什么这样计算时,大部分学生表示没有思考过这个问题,也说不清楚其中的道理。由此可见,学生对分数乘法计算只“知其然”——掌握算法,却“不知其所以然”——不明算理。
由此得到启示:教师要借助问题情境唤醒学生的相关知识经验,着力实现算法、算理的迁移、建构和融通。其中,理解分数乘法的算理是教学的重点和难点,教师在设计组织探究活动时要联系情境,合理、灵活运用几何直观,引导学生在多元表征中实现对分数乘法算理的深度理解。在教学时,教师还要注重引导学生在对比、联结中体会数与运算本质的一致性,发展其运算能力。
二、深度解读内容,整体架构单元学习
小学阶段数的运算包括整数、小数和分数的四则运算。《义务教育数学课程标准(2022年版)》指出,数的运算教学应注重对整数、小数和分数四则运算的统筹,让学生进一步感悟运算的一致性。为此,教师更要以结构化的思想设计实施单元整体教学,为学生提供结构化的学习内容,有意识地搭建对比、联结的桥梁,以达成感悟运算一致性的目标。本单元的整体教学基本是按教材原来的安排开展课时教学,其结构化主要体现在整体结构思想的统摄与联通上。“分数乘法”单元结构化教学设计见表1。
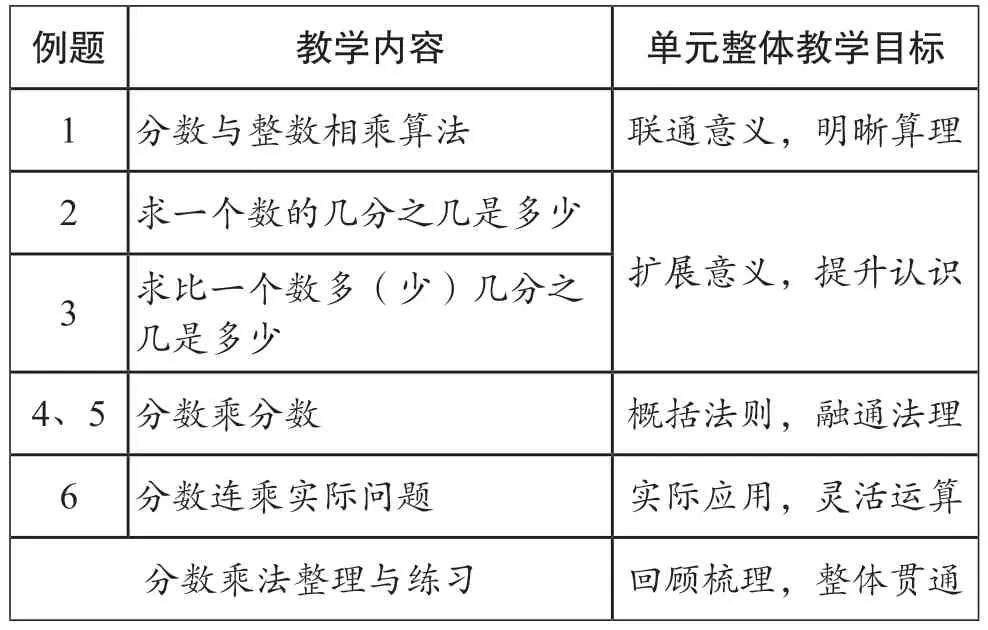
表1 “分数乘法”单元结构教学设计
例题1的教学主要是迁移原有运算概念,让学生理解求几个相同分数的和可以用乘法计算,感悟算法背后的算理;例题2着重教学用分数乘法求一个数的几分之几是多少,是对乘法概念的重要拓展,其意义与求一个数的几倍是多少是一致的,例题3在此基础上进行拓展;例题4、例题5教学分数乘分数的计算法则,并在此基础上概括分数乘法的计算法则,理解分数乘分数的算理是本单元的难点;例题6是在解决实际问题的过程中引出分数连乘的算式,再进一步培养学生的运算能力;最后,通过对单元知识的整体回顾与梳理,进一步形成结构化的整体认识。
三、组织深度探究活动,落实核心素养
深度的探究活动有助于学生把握知识本质,领悟数学思想,不断提升数学思维能力,发展数学核心素养,成为能独立思考、协作沟通、批判思辨、富有创造性的学习者。
(一)融通理、法,提高运算能力
数的运算是小学数学教学中的重要组成部分。运算能力不仅体现在能根据法则和运算律进行正确运算的能力,更体现在对算法与算理之间的关系的理解,能选择合理简洁的运算策略解决问题等方面。学情前测显示学生具备将整数乘法意义迁移至分数乘法的探究能力,也能将分数乘整数理解为“几个相同加数的和”,只是对算理的思考还不够深入,造成了算理不明的现状。在教学时,教师应着力引导学生感悟知识间的联系、算式与图形之间的联系,进而明晰算理。
【教学片段1】
那天之后,丸子突然发现自己变成了幸运的人。上班的时候,丸子能买到早餐了,很多人都买不到的生煎包,都被她买到了最后一份。下班的时候,丸子总能打到车了,即使是发布了橙色预警的台风天,她都顺利打到了车。司机不仅给淋了雨的丸子递上毛巾和水,下车的时候,还借给丸子一把伞。
师:我们班大部分同学都用了这种方法,老师有个疑问——为什么分母不变,整数与分子相乘呢?谁能试着解释一下?
师:我们一起来看,仔细观察,你明白其中的意思了吗?
师:结合直观图(出示图2),联系刚才几个同学的发言,你发现分母不变,整数与分子相乘的道理了吗?
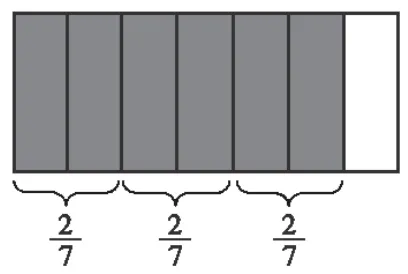
图2
上述教学从分数的意义着手,联系乘法的意义,借助直观图形,引导学生探索分母不变、整数与分子相乘的奥秘,让学生在直观表征和语言表达中进一步理解分数乘整数的意义,进而明晰分子与整数相乘就是在计算有几个分数单位,而累加的过程中分数单位是不变的,所以分母不变。
(二)数形互译,强化直观意识
落实直观教学,让算法可见,让算理可视,让学生真正理解分数乘分数的意义是一大难点。在引导学生探索×的计算方法时,笔者着重引导学生通过折一折、画一画,经历完整过程:先把单位“1”平均分成2份,取其中的1份;再把取到的1份平均分成4份,这样取其中的1份就是单位“1”的的。在此基础上,×就是按×先取1份,再取3份,也就是取3个。(如图3)

图3

图4
像这样通过动作直观、几何直观,就能让学生在体验中认识、理解什么是“分了再分,取了再取”,进而更好地理解算理。
基于单元整体教学,在一次次应用直观图示探究算理的过程中,学生不断感受到几何直观对于理解、掌握数学知识的重要价值,不断积累相关的活动经验,长此以往,应用几何直观就会成为学生探究新知、解决数学问题时的自觉意识。
(三)精心设计,实现结构化理解
结构化理解追求知识学习的主动关联、对比思辨、系统建构、迁移生长等,从而通过整体把握实现对数学知识的深度认识。在日常教学中,教师要运用“结构化理念”钻研教材,设计教学活动,引领学生展开结构化学习,注重将思维状态由散点分布转变为结构化呈现,实现知识的整体建构。
1.迁移拓展,意义联结
从“几个几分之几是多少”到“求一个数的几分之几是多少”是对乘法意义十分重要的一次拓展。从本质上来讲,“求一个数的几分之几”和“求一个数的几倍”在意义上是相同的,在算法上是相通的。因此,在单元主题学习中,教师要有意识地寻求有效路径以实现不同类型乘法之间的有效整合与沟通,实现知识体系的整体架构。
在执教“简单的分数乘法实际问题(1)”例2知识点时,笔者对教材内容进行了调整,如表2所示。

表2 教材例2知识点调整
从“唤醒”到“拓展”,红花和黄花都在与绿花进行比较,不管是“2倍”还是“”,虽然一个是整数,一个是分数,但都表示了与绿花之间的倍数关系。“一个数是另一个数的几分之几”与“一个数是另一个数的几倍”其内在意义是一致的,都表示两个数相比较的一种相除或相乘关系,学生由绿花的2倍可以用绿花的朵数×2表示,自然联想到绿花的就可以用绿花的朵数×来表示,由此便开启了乘法意义的拓展之旅。
最后,通过“联想”为学生充分理解、自主建构分数乘法的含义提供丰富而充分的感知材料,引导他们归纳得出分数乘法的意义,即“求一个数的几分之几是多少”可以用乘法计算。
伴随问题情境的层层变化,通过核心问题的引领,学生进一步体会分数乘法和整数乘法的一致性,并结合分数的意义,借助几何直观架构整数乘法计算方法与分数乘法计算方法之间的联系,这样的学习是基于结构化的学习,是促进学生思维发展的深度学习。
2.回顾唤醒,凸显本质
在整理回顾环节,教师引导学生回忆已经掌握的整数乘法和小数乘法的算法、算理,将它们与新学的分数乘整数进行比较,在求同存异中寻找三者之间的联系,进而明确分数乘法和整数乘法、小数乘法的本质是一致的,乘法就是在计量有几个这样的计数单位。
【教学片段2】
师:让我们回头想一想,在学习分数乘法之前,我们还学习过整数乘法和小数乘法,你觉得它们的计算原理一样吗?请你们结合70×3,0.7×3,还有今天学习的×3想一想。同桌两人可以先讨论一下。
生1:70×3中70表示7个10,7个10乘3就是21个10,就是210。
生2:0.7×3中0.7表示7个0.1,7个0.1乘3就是21个0.1,也就是2.1。
生4:我发现他们都是在算有几个单位,70×3是有几个10,0.7乘3是有几个0.1,×3是有几个。
师:看来不管是以前学的,还是今天学的乘法,都是在算有几个这样的计数单位。
像这样,通过引导学生回顾比较,举例说理,乘法的运算意义被进一步凸显,基于运算本质的乘法知识整体架构也逐渐完成,这样的学是有意义的学,这样的学也是有深度的学。
综上所述,本单元主题教学的研究主要落实在推动学生对分数乘法算理的深度理解,分数乘法与整数乘法、小数乘法的深度联结,力求依次推动学生运算能力、推理能力、几何直观等数学核心素养的提升。
