基于多源数据融合的配电网拓扑识别方法研究

刘祥波,王 森,延 凯,扈佃爱,高 芳,梁 伟

(国网日照供电公司,山东 日照 276826)

0 引言

配电网[1]发生故障或实施最优控制时,分段开关和接触网执行操作动作,使配电网拓扑结构[2]发生变化。由于配电网远程传输数据中存在信息缺失、虚假等问题,甚至某些节点缺乏通信通道,需要人工检查和报告,导致系统中存储的网络拓扑不能实时更新,降低了配电网安全、经济运行的速率。近几年,网络、大数据、物联网、通信[3-5]等技术飞速发展,通过安装测量设备可实时检测配电网基本电力数据信息,并根据这些数据信息识别配电网拓扑。

大量学者针对数据驱动下配电网拓扑识别方法进行了研究。文献[6]依托高级量测体系(advanced metering infrastructure,AMI)提供的电量信息,提出了1种仅通过配电网节点电压及功率数据驱动的中低压配电网拓扑识别及线路阻抗估测方法。文献[7]提出了1种联合低频短时电流脉冲信号传输路径追溯和高频电力线载波测距的中压配电网拓扑识别方法。文献[8]提出了1种基于数据驱动技术的配电网拓扑结构及线路参数识别方法。该方法通过配电网等效拓扑结构提取数据驱动参数,利用诺顿定理优化识别配电网的线路参数结果。然而,大部分拓扑识别方法都要求配电网配备高成本同步相量测量装置(phasor measurement unit,PMU),并提供大量的历史数据,如电压幅值、相位角等。这在实际配电网中难以实现。现有配电网测量系统主要由数据采集与监视控制(supervisory control and data acquisition,SCADA)系统、AMI和PMU组成。这些测量方法为配电网拓扑识别提供丰富的数据源。然而,SCADA覆盖率良好,但数据精度较低;PMU数据精度高,但覆盖率低;AMI覆盖率高,且数据精度高,但采样周期长。三者均不能满足电力系统的实时性要求。

考虑到配电网中测量终端数量越来越多,不同类型的测量设备为配电网运行控制提供了重要的基础数据。然而,丰富的数据也带来了问题,如数据时空维度、精度等不统一和数据利用率低等。为改善这些问题,本文提出了1种基于多源数据融合的配电网拓扑识别方法。

1 配电网测量系统

配电网在由主干线和分支线组成的复杂树形网络辐射供电模式下正常运行。变电站馈线由主干线分段供电。负载通过分支线连接到最近的变电站。

配电网测量系统的空间配置如图1所示。

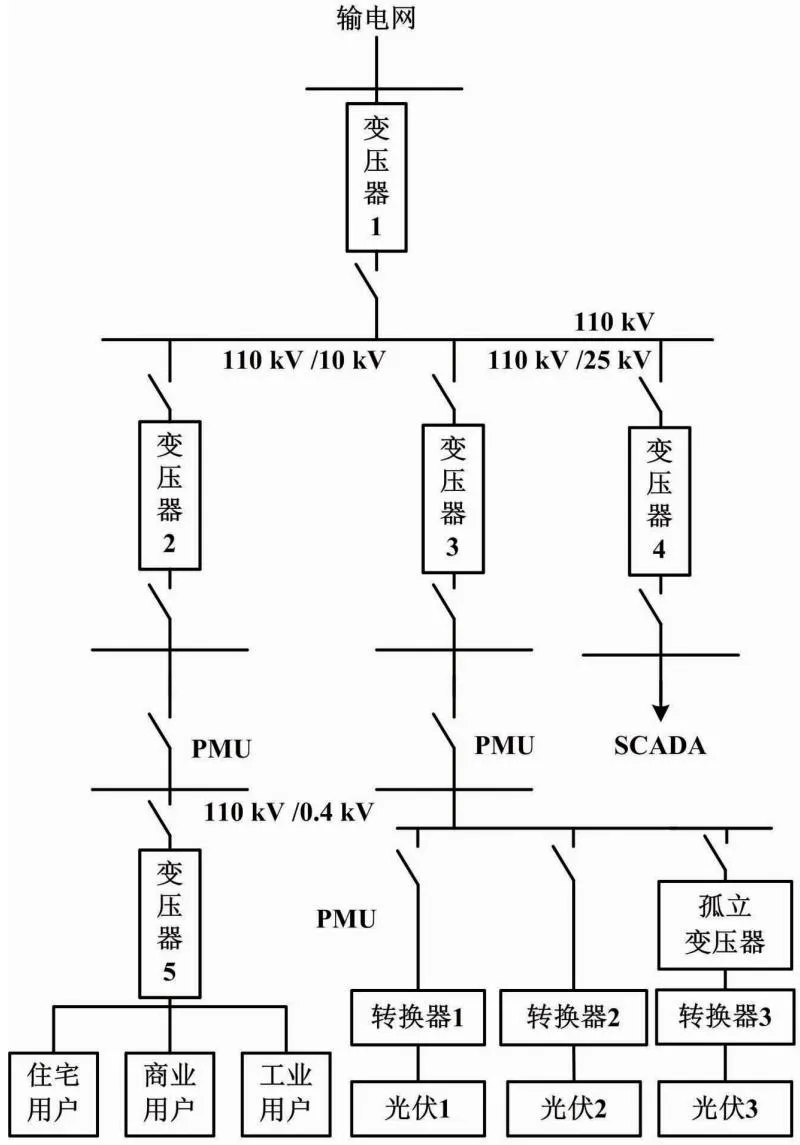
图1 配电网测量系统的空间配置图

配电网测量系统中,SCADA测量数据一般通过远程测控单元(remote terminal unit,RTU)采集。SCADA系统是电力管理系统的重要子系统,通常安装在馈线开关、配电变压器出口、开闭站和环网柜中。

SCADA测量的远程信号信息包括节点注入功率、支路功率、节点电压幅值、支路电流幅值和开关量等。其数据采集时间为2～5 s。

PMU通常安装在配电网干线的根节点、动态负荷接入节点、接触开关和其他重要节点,可测量节点电压相量和支路电流相量等动态数据。PMU采集间隔为10 ms或20 ms。PMU可以接收全球定位系统(global positioning system,GPS)信号,为同步测量数据添加时间刻度。PMU计算可以获得功率、相位、功率角等信息。

AMI主要采集用户端智能电表的数据,可以获得用户的粗略时间尺度的测量值,并对电能进行远程测量和能耗分析。AMI测量包括节点电压幅值、支路电流幅值、节点注入功率和支路功率。AMI采集速度相对较慢。其采样周期为15 min或30 min。

2 多源数据融合

2.1 多源数据时间同步

由于AMI、SCADA和PMU数据的时间尺度不同,无法准确反映配电网的真实情况。因此,需要选择标准数据源作为基准,并同步其余数据源的测量数据。

PMU数据的采样周期和传输延迟为毫秒级,且采样周期与传输延迟在GPS时间基准下严格同步。因此,本文将PMU作为时间基准标度。AMI数据虽采样周期长,但精度高,并且具有时间刻度。根据时间刻度,AMI数据可以与PMU数据对齐。然而,SCADA数据没有统一的时间尺度。SCADA具有不同的采样速度,并可以确保在相同的时间段后,对采样周期长度数据进行插值。SCADA根据周期长度依次插值采样周期长度的数据,从而使多段数据测量的采样周期一致。

2.2 基于线性外推的伪测量生成

本文令zm、zn和zp分别为PMU、SCADA和AMI的测量数据。

不同测量系统的数据采集频率如图2所示。

图2 不同测量系统的数据采集频率示意图

本文令zm(m为PMU的数量)的采样周期为Tm,则zn的采样周期Tn为:

Tn=rTm

(1)

式(1)表明,zm在2个连续的zn采样点之间采样r次。同理,zp的采样周期Tp为:

Tp=sTn

(2)

式(2)表明,zn在2个连续的zp采样点之间采样s次。

根据前述分析,PMU数据的采样周期快,而SCADA数据和AMI数据的采样速度慢。在许多时间段没有SCADA数据和AMI数据,因此需要补充高精度伪测量数据,从而使PMU数据、SCADA数据和AMI数据同步。为此,本文采用线性外推法生成伪测量数据:

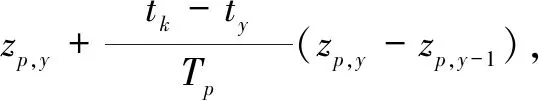
(3)

式中:zp,k为在时间ty和时间ty+1之间的任意时间tk的AMI伪测量数据。

(4)

式中:zn,k为在时间ty和时间ty+1之间的任意时间tk的SCADA测量值。

2.3 基于PMU的多源测量数据融合

本文假设Δt为PMU数据刷新率。其起始时间为t1、每个Δt间隔PMU产生测量数据zm,则有:

(5)

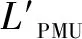
基于PMU生成的具有时间戳的精确数据可用于同步系统的SCADA测量数据。相同的配电网分区用相同的采样脉冲采集SCADA数据,从而确保SCADA数据时间同步。本文假设节点i的电压Ui可观测,则i的瞬时电压值为:

(6)

式中:ω为角频率;φ为主相角。

(7)

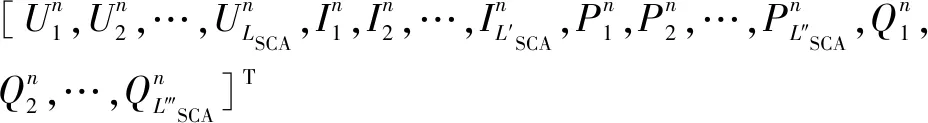
(8)

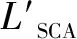
同理,AMI测量数据可以通过自身的时间标度和PMU数据同步。本文假设Δt′为AMI数据刷新率。每个Δt′时间段测量数据包括zm和zp,则:

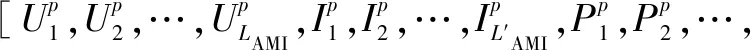
(9)

综上所述,对于具有多类型测量数据的配电网,因为各种测量系统的数据刷新频率不同,所以测量方程由PMU、SCADA和AMI多周期测量数据共同建立,以满足拓扑识别的要求。

3 多源数据融合拓扑识别模型

3.1 目标函数

本文基于加权最小二乘法构建了1种拓扑识别模型,从而最小化多个测量段的分支功率的测量值和估计值之间的加权误差。基于此,本文建立了如式(10)所示的目标函数。

(10)

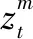
3.2 约束条件

拓扑识别模型的约束主要包括潮流约束和径向约束。对于分布式光伏配电系统,其潮流平衡方程为:

(11)

式中:Pi为i的有功功率;Ppv为光伏的输出功率;K(i)为i的子节点集;pi为i的有功负载;rij为线路i-j的电阻;Ω为节点总数。

(12)

式中:Qi为i的无功功率;qi为i的无功负载;xij为线路i-j的电抗。

本文引入潮流约束中的开关状态变量矩阵C。如果C中元素值为1,则表示线路i-j处于运行状态(连接),且功率从节点i流向节点j。基于上述分析,并综合考虑多个时间段内的测量数据,拓扑识别问题中的功率流约束更新如式(13)和式(14)所示。

(13)

式中:Pt,ij为单位时间t内流过线路i-j的有功功率;ct,ij为单位时间t内开关状态变量矩阵C中的元素;T为总时间。

(14)

式中:Qt,ij为单位时间t内流过线路i-j的无功功率。

此外,由于节点电压对拓扑识别模型的精度影响不大,并且会增加模型的求解时间,因此在模型的约束条件中不考虑节点电压的影响。

对于拓扑识别问题,通常已知的是节点的注入功率和具有测量装置支路的部分功率。考虑到设备的测量误差一般符合高斯分布,潮流约束可规定如式(15)～式(18)所示。

(15)

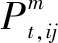
(16)

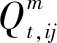
(17)

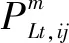
(18)

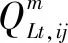
通过使用开关状态变量矩阵C,不仅可以描述配电网支路上的功率,还可以表示支路的流向。此外,本文仅考虑径向配电网的拓扑识别,因此需要增加分支数的约束,即节点数减去源节点数:

(19)

式中:E′为配电网线路集合;(i→j)为线路i-j的功率从i流向j。

然而,上述约束均属于非线性约束。根据极限定理,t处测量段支路的有功功率和无功功率的估计值存在上下限。因此对于t处测量段支路,有:

-ct,ijM≤Pt,ij≤ct,ijM

(20)

式中:M为任意大的正数。

当ct,ij为0时,表明线路i-j处于非运行状态,则Pt,ij为0;当ct,ij为1时,表明线路i-j处于运行状态,则Pt,ij在其上下限之间。

-ct,ijM≤Qt,ij≤ct,ijM

(21)

当ct,ij为0时,表明线路i-j处于非运行状态,则Qt,ij为0;当ct,ij为1时,表明线路i-j处于运行状态,则Qt,ij在其上下限之间。

4 仿真与分析

本节基于数值分析对提出的数据融合方法和拓扑识别模型进行评估。

4.1 仿真设置

仿真时硬件环境如下:采用Intel奔腾G4560中央处理器(centrol processing unit,CPU);内存64 GB;操作系统为Win1064位。软件环境为Matlab2019A。

IEEE 33节点测试系统如图3所示。

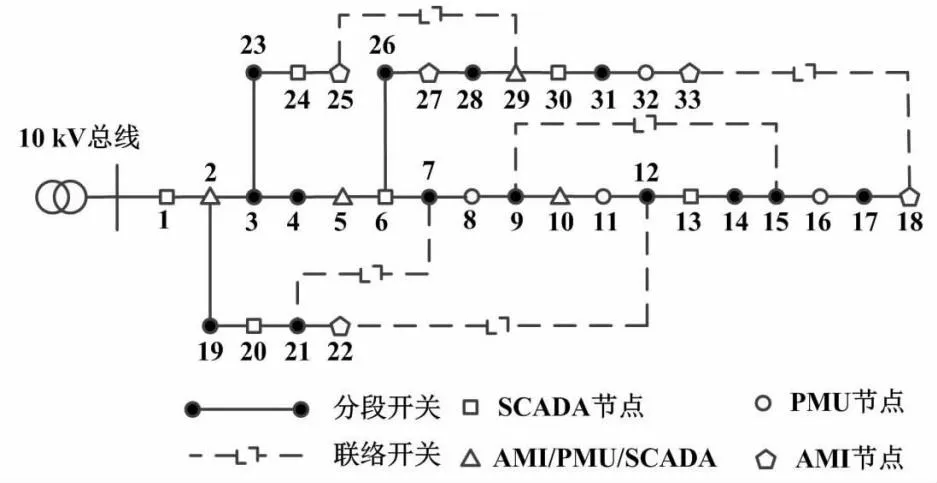
图3 IEEE 33节点测试系统示意图

本文采用图3所示的IEEE 33节点测试系统来验证所提方法的有效性。IEEE 33馈线系统的参考电压为12.66 kV、参考功率为10 MVA。馈线系统包括33个负荷节点、32个常闭分支和5条常开联络线。同时,系统中:某些节点配备光伏设备,以参与配电网络。系统中:节点1、6、13、20、24和30为SCADA测量节点,采样周期为10 s;节点2、8、11、16和32为PMU测量节点,采样周期为1 s;节点18、22、25和33为AMI测量节点,采样频率为1 min。本文将潮流计算结果添加到高斯噪声分布,以模拟所有测量数据。

(22)

对于具有最大误差η的测量装置,真实值μt,i′测量的标准偏差为:

(23)

4.2 数据融合分析

本文以IEEE 33节点测试系统获得的数据作为初始测量装置的测量数据,将时间尺度对齐和伪测量生成的数据用作多源融合数据。不同测量设备在节点2注入有功功率测量对比结果如图4所示。

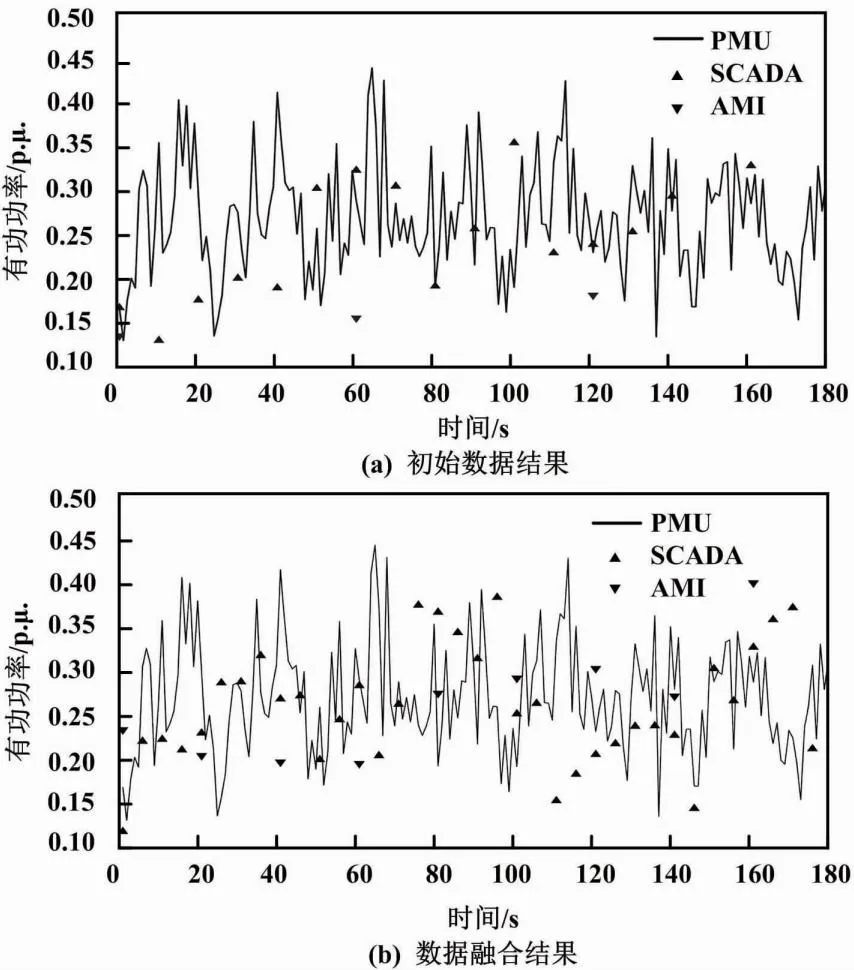
图4 不同测量设备在节点2注入有功功率测量对比结果

由图4可知,在测量装置收集的初始数据中,PMU的样本数据非常丰富,测量精度较高。然而由于SCADA和AMI的数据采集频率较低,采集的样本数据相对较少。同时,SCADA和AMI数据上传所需的时间较长,存储的数据不仅不够丰富,而且质量较差、误差较大。多源数据融合后,SCADA、AMI的样本数量和精度明显提升。这为后续配电网的快速拓扑识别奠定了良好的数据基础。试验结果验证了时间尺度对齐方法的有效性,以及伪测量数据的正确性。

4.3 拓扑识别结果分析

本文假设IEEE 33节点测试系统中线路2-19断开,联络线12-22闭合。在这种情况下,考虑到不同时间段和不同误差程度的测量数据,本小节对比了不使用融合方法以及使用融合方法下,拓扑识别准确率的结果。考虑到支路测量功率和节点注入功率组合对拓扑识别结果的误差不同所造成的影响,试验将每类误差组合分别进行100次拓扑识别,并取平均值作为最终结果。拓扑识别的精度A为:

(24)

式中:N为拓扑标识的数量;NC为正确标识的数量。

不同方法拓扑识别精度对比结果如表1所示。

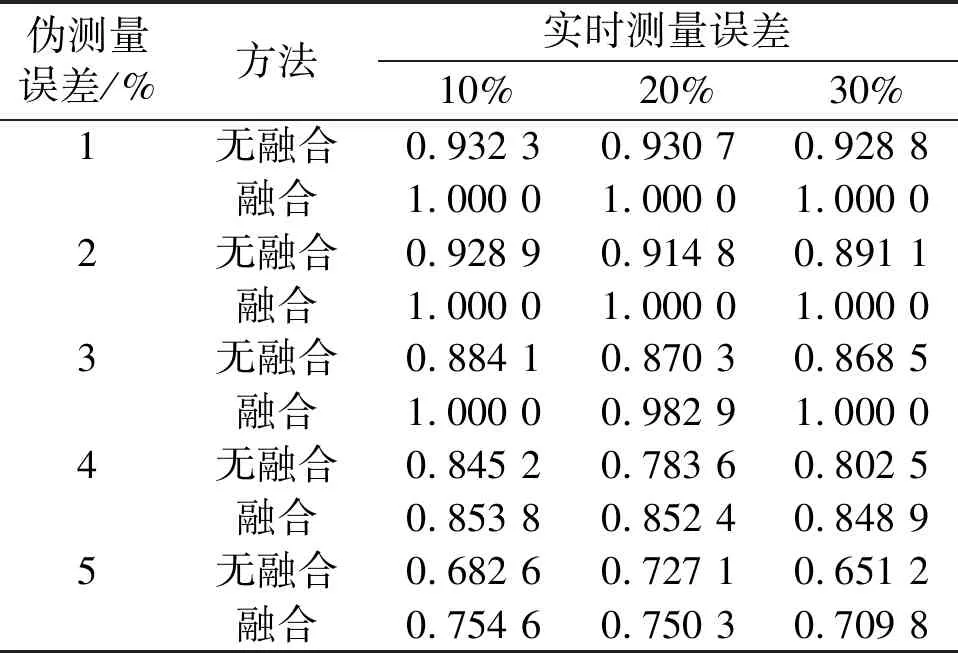
表1 不同方法拓扑识别精度对比结果

由表1可知,在测量误差2%以内:基于原始数据获得的拓扑识别结果精度在90%左右;基于所提多源数据融合的拓扑识别精度基本达到100%。仿真结果表明,多源数据融合可以显著提高配电网拓扑识别准确率。然而,当节点注入功率数据的实时测量误差增加到30%时,这2种情况下的拓扑识别精度都显著降低。在最坏情况(节点注入功率数据的实时测量误差为30%,伪测量误差为5%)时,多源数据融合方法拓扑识别精度为70.98%。与无融合方法相比,其精度提升5.86%。仿真结果进一步验证了所提方法对配电网拓扑识别具有较高的识别精度。

5 结论

本文对配电网拓扑识别过程进行了研究与分析,建立了1种基于多源数据融合的配电网拓扑识别方法。该方法利用多源数据时间同步、基于线性外推的伪测量生成和PMU多源数据融合方法对数据进行处理,并基于加权最小二乘法求解最优方案。经多源数据融合后,识别精度有所提升,表明所提方法的正确性及有效性。该方法可为配电网精细化管理提供助力,具有广阔的应用前景。