基于集群划分的配电网双层电压协调优化策略

杨 颂，王成龙，孙树敏，程 艳，于 芃

（国网山东省电力公司电力科学研究院，山东 济南 250003）

0 引言

随着可再生能源的快速发展，大规模分布式光伏不断接入配电网，由分布式光伏并网引起的配电网过电压问题愈加严重［1-2］，这不仅限制了分布式光伏自身的消纳，也严重威胁配电网的安全稳定运行［3-4］。

为解决配电网的过电压问题，众多学者对电压控制方法进行了研究。文献［5］提出了一种基于模型预测的电压控制策略，该策略利用有载调压变压器（on-load tap changer，OLTC）、静态无功补偿器和光伏逆变器将节点电压调节到安全运行范围内。文献［6］提出了一种基于逆变器电流裕度的配电网动态电压调节策略，在保持逆变器有功功率不变的条件下，通过最大无功功率输出对配电网电压进行主动支撑。文献［7］提出光伏逆变器恒功率因数控制策略，该策略在光伏出力最大时仍可输出无功功率，以此实现对配电网电压的调节，但该方法依赖光伏逆变器的无功容量，当逆变器无功容量不足时，配电网过电压问题可能得不到有效解决。文献［8］提出减切有功功率、增加无功功率的配电网电压调节方法，通过光伏逆变器有功、无功调节解决配电网过电压问题。上述电压调节方法主要为集中式的电压调控方式，这适合于节点数量较少的配电网。当大规模的分布式光伏接入配电网时，配电网内节点数量将急剧增加，电压控制模型中控制变量也大幅增加，若仍然采用集中控制的控制方式，电压控制过程将会因高维的变量维度而变得复杂，电压优化控制无法满足控制时间尺度的要求。

为解决电压控制变量复杂及电压优化控制无法满足控制时间尺度的问题，当前研究主要通过集群电压控制解决。在配电网集群划分方面，文献［9］采用无功-电压灵敏性矩阵来描述节点之间的电气距离，并以此作为集群划分指标进行配电网集群划分。文献［10］将光伏的输出特性、空间位置、响应模式作为虚拟集群的划分指标体系。根据联络开关的状态，文献［11］提出了改进的遗传算法作为集群划分算法，以此获取最佳的集群划分。文献［12］则提出了基于Tabu 搜索算法的配电网集群划分算法，实现对配电网集群的划分。然而，由于这些算法不能自动形成最佳的集群数量，因此所得集群划分结果可能并不准确。在集群电压调控方面，文献［13］利用交替方向乘子法（alternating direction multiplier method，ADMM）来实现下游和上游集群之间的集群电压调节。文献［14］提出了“先无功调节最大化，后有功调节最小化”的集群电压调节策略，通过各集群内光伏逆变器的有功、无功控制实现配电网的电压调节。上述研究都能有效地解决配电网过电压问题，但在电压控制过程中只依赖光伏逆变器，忽略了其他调压设备的配合，电压控制的经济性难以保证。

基于上述分析，文中提出了一种基于集群划分的配电网双层电压控制方法。将质量耦合函数作为集群划分指标，并采用Fast-Newman 算法将配电网划分为若干集群。基于集群划分，上层建立集群日前优化调度模型，给出有载调压变压器与光伏逆变器的日前调度计划；下层建立集群实时二阶锥电压控制模型，通过实时调节光伏逆变器以最大化追踪日前调度计划，以此实现日前调度与实时电压控制的结合。

1 基于质量耦合函数的集群划分方法

1.1 质量耦合函数

社团分区算法为复杂网络的划分提供了一种有效思路［15-16］。与其他划分方法不同，社团分区算法可以自动生成最优的集群数目而无须事先设定。社团分区算法通常以模块度函数作为划分指标，但模块度函数因只能反映节点联系紧密程度而具有局限性［17］。为实现配电网集群的合理划分，将质量耦合函数作为配电网的集群划分指标。质量耦合函数由集群内耦合指标和集群间耦合指标组成。

1.1.1 集群内耦合指标

式中：Kin为集群内耦合指标；T为配电网内集群总个数；πα为配电网内第α 个集群；N为配电网中的节点数；Nα为配电网第α 个集群内的节点个数；Aij为节点i与节点j之间的功率-电压灵敏度，可以描述节点i和节点j之间电压调节耦合度。

式中：Δδ为节点相位角变化矩阵；ΔU为节点电压幅值变化矩阵；ZPδ、ZQδ分别为节点相位角对节点注入有功、无功功率的灵敏度矩阵；ZPU、ZQU分别为节点电压幅值对节点注入有功、无功功率的灵敏度矩阵；ΔP、ΔQ分别为节点注入有功、无功功率的变化矩阵。

由式（3）可知，集群内耦合指标Kin取值范围为（0，1），其值越大，表示同一集群内部各节点之间电压调节耦合度越高。

1.1.2 集群间耦合指标

式中：Ko为集群间耦合指标，其取值范围为（0，1），Ko越小表征不同集群中的节点之间电压调节耦合度越差，而各集群内部电压的独立控制也越难实现。

基于上述集群内耦合指标和集群间耦合指标，提出质量耦合函数KC。

式中：KC的取值范围为（0，1）。随着KC的增大，同一集群的节点之间具有较强的电压调节耦合度，而不同集群间的节点具有较差的电压调节耦合度，各集群内部电压越容易实现独立控制。因此质量耦合函数的取值越高，集群划分的结果越合理。

1.2 Fast-Newman集群划分算法

在社区发现算法中，通过社会或物理关系，利用节点聚合的方式可形成社区结构［20］。为形成一个合理的社区（或集群），具有强耦合性的节点应属于同一集群，不同集群中的节点应该具有较差的耦合性。社区（或集群）应反映配电网的结构特征（如线路的电阻和电抗），并揭示配电网内各节点间的关系（如功率-电压灵敏度）。在社区发现算法的基础上，采用Fast-Newman 算法来寻找社区结构，实现配电网集群的快速划分，具体步骤如图1 所示。

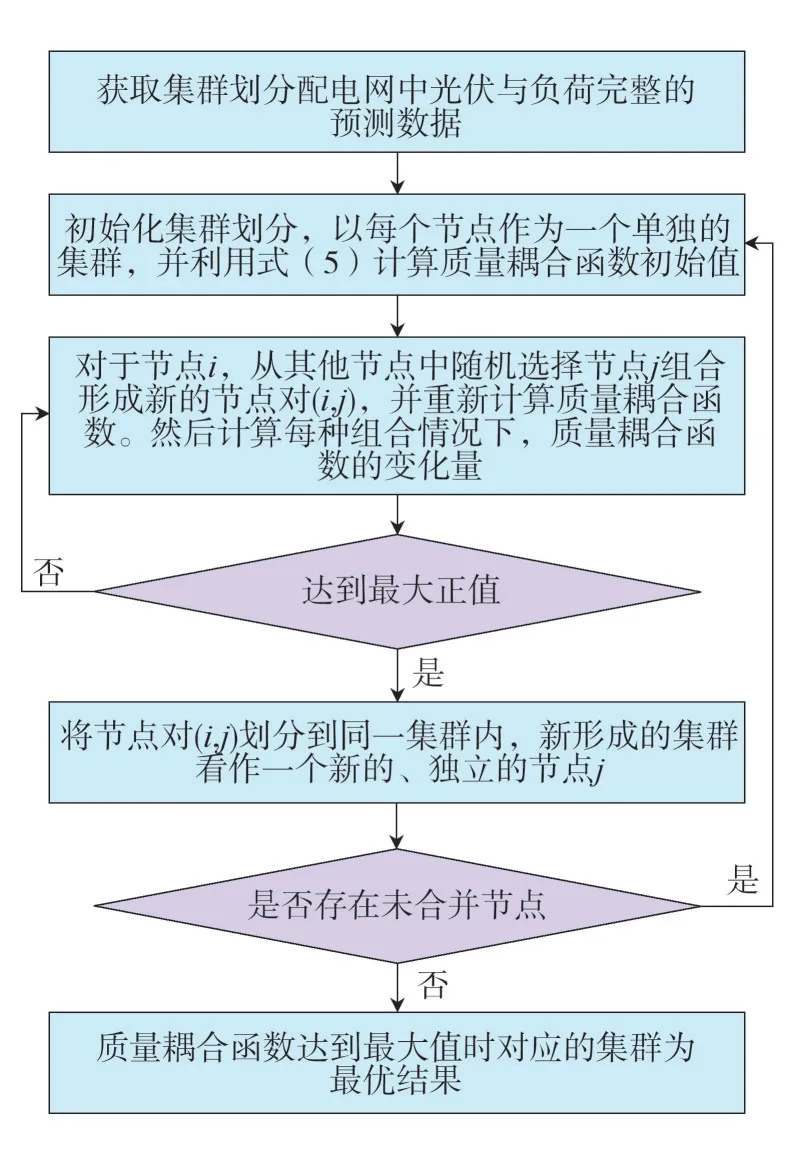
图1 集群划分流程Fig.1 Flowchart of the cluster partition

步骤1：将配电网中的每个节点视为一个集群，根据式（5）计算质量耦合函数初始值KC_0。

步骤2：在所有节点中随机选择一个节点对（i，j）并合并为一个新的集群，计算此时的质量耦合函数KC_1，同时计算出质量耦合函数的变化值ΔKC_1=KC_1-KC_0。

步骤3：所有节点对重复进行步骤2，将ΔKC_1最大的节点对定义为最终的新集群，并且该节点对视为一个新节点。

步骤4：重复步骤1—步骤3，当所有节点对的质量耦合函数值不再增加时，停止集群划分过程，此时耦合函数值取得最大值，对应的集群划分结果即为最终的最优划分结果。

2 集群日前调度模型

2.1 目标函数

设配电网通过快速集群划分方法被划分为T个集群，由于不同集群间具有较低的电压调节耦合度，因此每个集群的电压控制可以独立进行。配电网的电压主要由光伏逆变器与OLTC 来调节。第α个集群中日前调度模型的目标函数为：

2.2 约束条件

1）OLTC 约束。

2）光伏约束。

3）配电网潮流约束。

为求解上述所提模型，采用改进的粒子群优化算法来进行优化，其详细求解过程可参见文献［21］。

3 配电网实时电压控制模型

由于大规模分布式光伏接入配电网，其输出功率变化将显著影响配电网的电压水平。如果调节电压只依靠日前调度，光伏的预测误差极可能导致配电网发生过电压现象。如果在实时运行时能依据网络实时运行数据对日前调度进行修正，不仅可以保证配电网运行的经济性，还可以有效避免光伏功率预测误差对配电网电压调节的负面影响。有载调压变压器的分接头在一天内不能超过允许动作次数，且在短时间内不能频繁调节，而光伏逆变器并不存在这些问题，因此在实时运行阶段，主要通过调节光伏逆变器修正日前调度计划。对于含有大规模分布式电源的配电网，光伏安装规模大且位置分散，若采用传统集中式的方法将会大幅增加电压控制模型的变量维度，增加优化过程的复杂性，无法满足电压控制实时性的要求。为解决上述问题，提出一种基于集群划分的二阶锥实时电压控制策略。该策略在第α 个集群下的目标函数为

该策略的优化目标是最大化第α个集群的日前调度值。该模型的约束条件包括式（12）—式（16）和以下约束：

式中：ui,t为t时刻节点i电压幅值的平方；uj,t为t时刻节点j电压幅值的平方；iij,t为t时刻流过线路i-j的电流的平方。

4 配电网双层电压控制策略实现过程

随着大规模分布式光伏的不断接入，配电网的电压控制将变得越来越复杂。基于配电网集群划分，提出配电网双层电压控制策略，上层在日前调度阶段优化配电网内有载调压变压器与光伏的计划调度值，下层通过优化光伏逆变器的无功功率和有功功率来实时纠正日前调度计划，实现流程如图2 所示，具体过程如下。

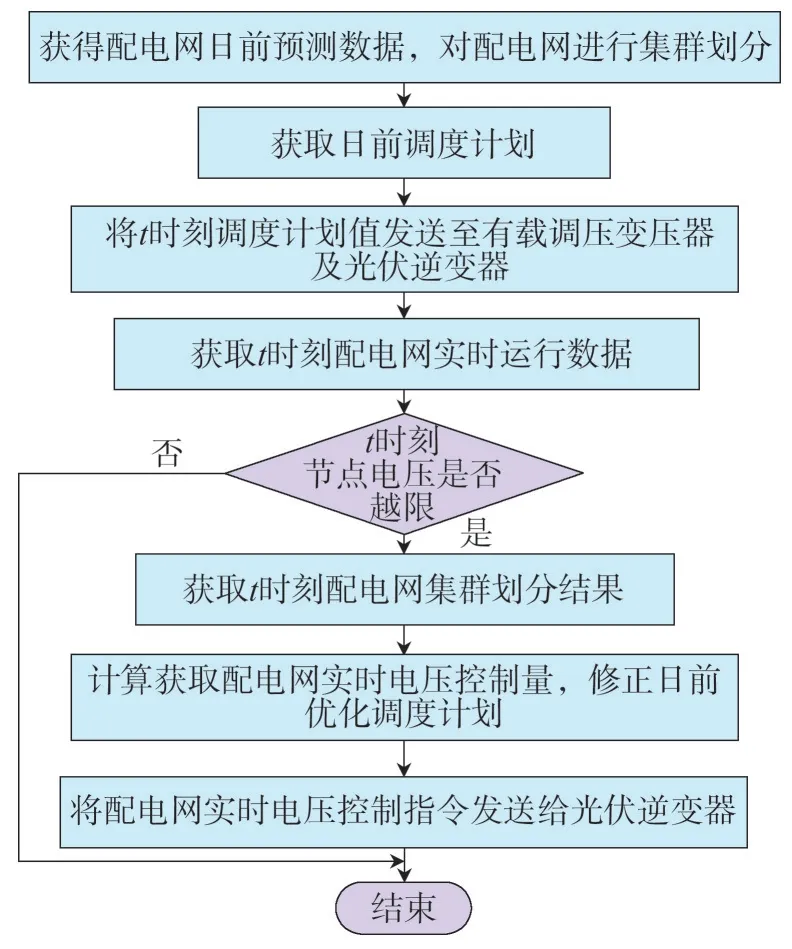
图2 控制策略流程Fig.2 Flow chart of the proposed strategy

步骤1：获得配电网日前预测数据，并根据式（5）对配电网进行集群划分。

步骤2：建立集群日前优化调度模型，计算获取配电网日前优化调度计划，将日前调度计划发送至各有载调压变压器及光伏逆变器。

步骤3：在实时运行阶段收集配电网的实时运行数据。

步骤4：若t时刻配电网节点电压在日前调度的控制指令下超过了正常范围，则进行步骤5，否则结束该时刻电压控制进程。

步骤5：依据实时运行数据计算获取配电网实时电压控制量，通过实时电压控制来修正日前优化调度计划。

步骤6：将配电网实时电压控制指令发送给光伏逆变器，并结束电压控制。

5 算例分析

5.1 算例参数

采用某一实际馈线作为分析对象，验证所提电压控制方法的有效性，该馈线为10 kV 三相平衡系统，共有69 个节点，其拓扑结构如图3 所示。馈线上的总负荷为17.6 MVA，总光伏安装容量为8.6 MW。

图3 算例拓扑结构Fig.3 Topology of the feeder system

图4（a）中给出了馈线所在地太阳辐照度及负荷需求的预测曲线。图4（b）中给出了馈线有载调压变压器的一次侧电压。馈线中各节点光伏的装机容量如图5 所示。

图5 光伏安装容量Fig.5 Installed PV capacity in each node

在OpenDSS 仿真平台对该馈线进行建模，通过MATLAB 软件调用该模型进行仿真分析。为验证所提出的方法能够有效地解决配电网的过电压问题，选取2022 年太阳辐照度最强的一天作为分析场景。图6 为配电网在太阳辐照度最强的一天、无任何调压措施下的节点电压分布，由图6 可知配电网某些节点在中午时刻出现了过电压现象。为保证配电网的安全运行，需要实施有效的电压控制策略。

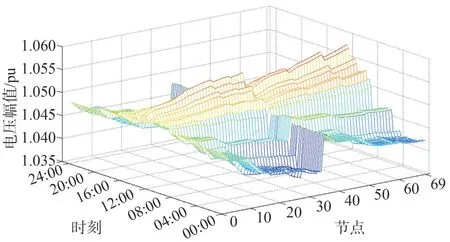
图6 10 kV馈线一天内的节点电压分布Fig.6 Nodal voltage distribution of 10 kV feeder during a day

5.2 集群划分分析

为解决配电网过电压问题，先要对配电网进行集群划分。选择12：30 时作为典型场景，分析所提的集群划分策略。在所提集群划分策略下，质量耦合函数值与集群划分数量关系如图7 所示。由图7可知，当质量耦合函数达到最大值0.822，馈线被划分为6 个集群，因此最佳集群数目是6。在图3 中，最终的集群划分结果由红色虚线框标记，集群表示为｛π1，π2，π3，π4，π5，π6｝。从集群划分的结果来看，集群划分结果与配电网节点的地理属性相关，这是因为不同节点之间功率-电压灵敏度与节点之间的阻抗相关，而节点之间的阻抗又与节点之间的地理属性直接相关。

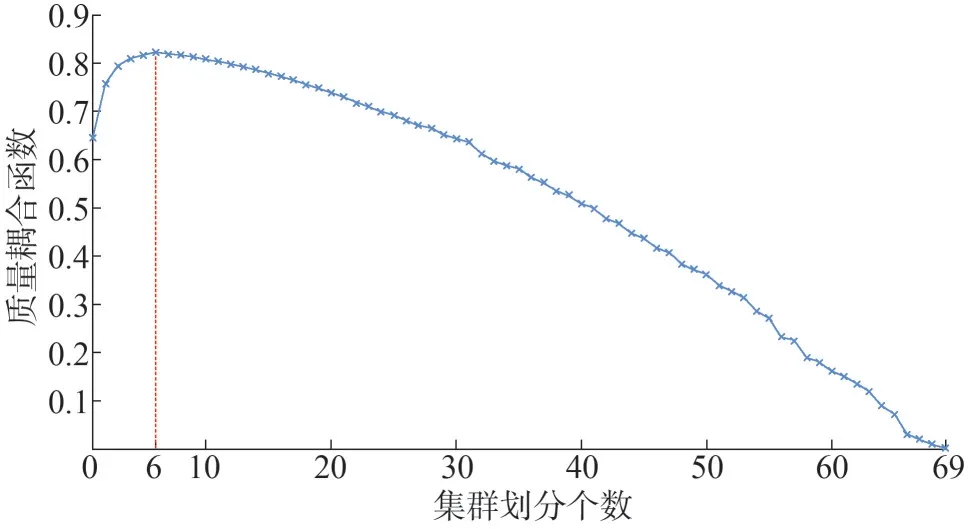
图7 不同集群划分下耦合质量函数值Fig.7 Coupling quality function corresponding to different clusters

为分析所提集群划分指标的优越性，采用模块度函数［17］与质量耦合函数进行比较，两种指标下集群划分结果对比如表1 所示。其中，模块度函数下馈线共被分为8 个集群，规模最小的集群（π2）包含4个节点，而规模最大的集群（π7）包含12 个节点，由上述结果可知采用模块度函数得到的集群在规模上具有较大的差异性。而采用质量耦合函数进行集群划分，馈线被划分为6 个集群，规模最大的集群（π1）包含15 个节点，而规模最小的集群（π2、π6）包含9 个节点。显然，采用质量耦合函数所得集群在规模上差异较小，集群划分规模更加均衡，这是由于所提方法中的内部耦合度指标和外部耦合度指标可以平衡集群大小，避免集群规模不均衡，因此采用质量耦合函数划分的集群更为合理。

表1 不同方法下的集群划分结果Table 1 Results of cluster partition with different methods

为进一步验证所提集群划分方法的有效性，在两种集群划分指标下均采用所提电压控制策略，两种方法下配电网电压调节成本如表1 所示。可以看出，在采用质量耦合函数得到的集群划分结果下，配电网电压调节成本较小，调节成本的差异证明了质量耦合函数可以为后续的电压控制提供更加合理的集群划分结果。

5.3 配电网电压控制效果分析

在对馈线进行集群划分后，采用所提电压控制方法解决配电网的过压问题。根据预测数据获取有载调压变压器及光伏逆变器的日前调度计划，在日前调度计划的基础上采用实时电压控制策略对日前调度计划进行实时修正。

在所提策略下，图8 给出了有载调压变压器在一天内的运行情况。由图8 可以看出，有载调压变压器的抽头位置在一天内总共调整了两次，这是因为在11：00—14：00，馈线上节点过电压严重，仅依靠光伏逆变器调节无法解决节点过电压问题，有载调压变压器必须参与电压调节才能将配电网节点电压调节至安全运行范围内。

图8 OLTC一天内的运行情况Fig.8 Operating performance of the OLTC in a day

在所提电压控制方法下，各节点光伏逆变器有功控制的日前调度计划及实时控制结果如图9 所示，各节点光伏逆变器无功控制的日前调度计划及实时控制结果如图10 所示。从图9 和图10 可以看出，日前调度计划下的节点光伏调节优化结果与实时控制阶段的优化结果存在差异，这是因为由于预测误差的存在，仅依靠日前调度计划不能将配电网电压调节至安全运行范围内，必须通过实时电压控制来修正日前调度计划以保证配电网的安全稳定运行。

图9 不同方法下光伏逆变器的无功功率吸收情况Fig.9 Absorbed reactive power of the PV inverters with different method

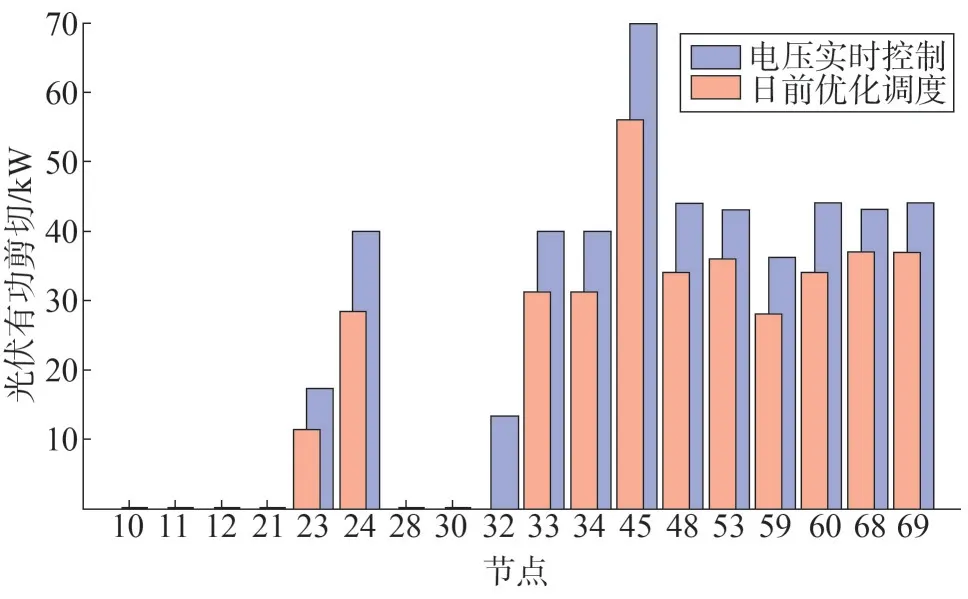
图10 不同方法下光伏剪切功率Fig.10 Curtailed PV active power with different method

图11 为所提方法下12：30 的节点电压分布情况。如图11 所示，由于预测误差存在，实时的光伏输出比预测值要大，仅靠日前调度计划无法有效解决配电网内的过电压问题，节点过电压仍然存在。在实时阶段采用所提实时电压控制策略后，馈线内所有的节点电压都被调节至安全运行范围内，这可以验证所提电压控制方法能有效地解决配电网过电压问题。

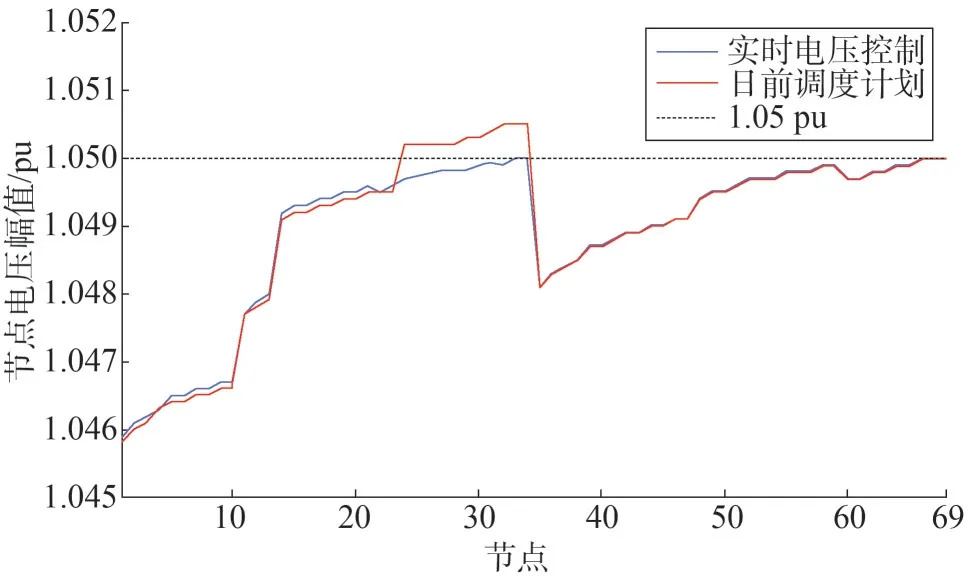
图11 所提方法下的节点电压Fig.11 Nodal voltage with the proposed method

为进一步分析所提策略的有效性，采用集中式电压控制进行比较分析。在集中式电压控制中，整个馈线被视为一个集群进行调节，并在此基础上进行日前调度计划与实时电压控制。两种方法下的节点电压分布如图12 所示。由图12 可以看出，这两种方法均能将电压控制在安全运行范围内。

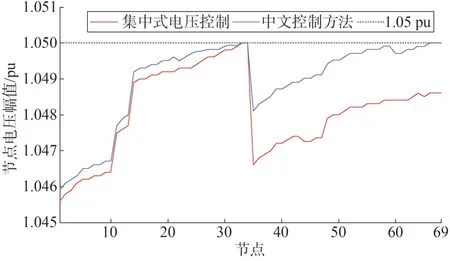
图12 两种方法下的节点电压Fig.12 Nodal voltage with the two methods

表2 给出了两种方法下的有载调压变压器和光伏逆变器优化控制结果，其中ρ为光伏逆变器无功调节量，ω为光伏有功剪切量，τ 为变压器抽头位置调节次数，ε 为电压控制优化计算时间，σ为二阶锥松弛误差。在集中式电压控制下，光伏逆变器的总调节无功功率为1 835.74 kvar，而光伏逆变器的总调节有功功率为229.91 kW。而在所提控制方法下，光伏逆变器的总调节无功功率为1 393.12 kvar，光伏逆变器调节的总有功功率为473.91 kW。相比集中式电压控制方法，电压控制剪切的光伏有功输出更少，但需要更多的无功功率来解决节点过压问题。此外，从表2 可以看出，在集中式电压控制方法下，有载调压变压器的抽头位置在一天内变化6 次，但在所提方法下，有载调压变压器的抽头位置只调节2次，由此可见文中方法大大减少了有载调压变压器的抽头位置的变换次数，这有助于延长有载调压变压器的使用寿命。

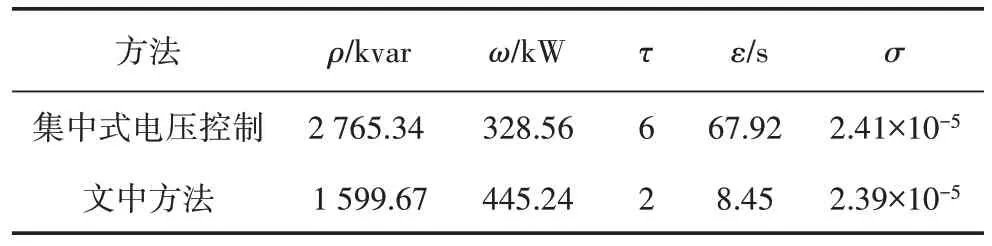
表2 两种方法下的优化控制结果Table 2 Optimized control results with two different methods

为进一步说明文中方法在计算性能方面的优越性，表2 也给出了两种方案下的电压控制优化计算时间与文中模型的二阶锥松弛误差。由表2 可知，在二阶锥松弛模型下，二阶锥松弛误差精度能够达到10-5量级，说明文中方法可以达到足够高的精度，满足确切性要求。此外，由表2 可知，在集中式电压控制方法下的优化计算时间为67.92 s，而在所提方法下计算时间只需8.45 s。所提方法的计算时间比集中式电压控制方法下的计算时间大大减少。这是由于集中式电压控制方法下所有的光伏逆变器都参与了电压控制，这大大增加了优化的复杂性。而所提方法是在每个集群内进行建模并优化，电压优化控制的模型可以极大简化，电压优化求解时间也可极大缩减，符合实时电压控制对时间尺度的要求，更加适用于未来大规模分布式电源接入的配电网电压控制。

6 结束语

为解决大规模分布式电源接入配电网引起的过电压问题，提出了一种基于集群划分的配电网双层电压控制策略。选取质量耦合函数作为配电网集群划分指标，并采用Fast-Newman 算法对配电网进行快速集群划分。基于集群划分，上层建立集群日前优化调度模型，下层建立集群实时二阶锥电压控制模型，通过实时调节以最大化追踪日前调度计划。所提策略实现了日前调度与实时电压控制的结合，可以保证配电网的安全稳定运行，提高配电网未来对大规模分布式光伏的接纳能力。