计及线性化潮流约束的主动配电网运行优化

2024-04-07丁月明张学清崔荣喜李明冰许家余

山东电力技术 2024年3期

丁月明，张学清，崔荣喜，李明冰，许家余

（1.国网山东省电力公司日照供电公司，山东日照 276800；2.国网山东省电力公司烟台供电公司，山东烟台 264000；3.山东大学电气工程学院，山东济南 250061）

0 引言

主动配电网（active distribution network，ADN）可以实现各种分布式电源（distributed generation，DG）的灵活接入。但具有随机波动特性的可再生能源（renewable energy sources，RESs）在大规模并网中为电力系统带来清洁能源的同时，也为ADN 的安全经济运行带来了新的运行挑战［1-4］。

光伏发电和风力发电作为主要的可再生能源发电技术，被广泛地应用于配电网运行优化中，得到了广泛的发展。文献［5-6］计及分布式电源和负荷的不确定性，通过源网荷储的协调优化，提出一种面向主动配电网的综合优化模型，表明了源网荷储的协调优化能提高系统应对可再生能源发电的不确定性，提高系统运行灵活性，促进可再生能源消纳。文献［7］构建了一种计及光伏发电的配电网无功优化模型，可以有效提升系统的电能质量、运行稳定性与系统经济性。文献［8］构建一种考虑负荷裕度的ADN 运行优化模型，表明当负荷裕度均衡分布时，配电网应对负荷波动的能力较强，系统稳定性较高。文献［9-10］构建一种考虑储能系统的配电网运行优化模型，仿真结果表明所建模型可以充分发挥储能系统的运行灵活性，提高系统对可再生能源的消纳能力，提高系统运行灵活性。文献［11］提出一种含储能系统与柔性负荷的源荷储调度优化模型，仿真结果表明：合理配比储能系统与柔性负荷的容量可以提升系统对风电的消纳能力，促进可再生能源消纳。上述文献验证了柔性负荷具有调整负荷曲线的能力，平滑了负荷曲线，有效提升了配电系统的运行经济性。

交流潮流（AC load flow，AC-LF）方程是构成ADN 运行优化模型的基础。由于AC-LF 方程是非线性非凸的，在ADN 优化模型中又往往含有整数变量，使得待求解问题为典型的非线性混合整数规划（mixed integer non-linear programming，MINLP）问题，直接求解的难度较大［12-14］，计算时间较长，所以即使对于小型配电网模型，采用传统的MINLP 求解器也难以在短时间内获得最优解［15］。故对AC-LF 方程进行线性化近似处理是降低ADN 优化模型计算困难的有效方式之一，可解决上述交流潮流造成的问题，并使运行结果接近于非线性AC-LF 模型的结果，具有较高的计算效率［16］。文献［17］基于线性化的交流最优潮流约束，提出一种计及电压和网损约束的线性化潮流模型，提高了电网潮流的计算效率。文献［18］提出一种配电网潮流线性化方法，可以快速求解电压幅值和无功功率流。文献［19］提出一种配电网非线性潮流约束的线性化通式，并对多种配电网线性化潮流模型进行了误差分析。

在含可再生能源发电的配电系统运行优化中，需要处理源侧、荷侧等多种不确定性因素。文献［20］采用区间数描述负荷和电源的不确定性，并通过场景分析法获取最优调度方案。文献［21］针对分布式电源和电动汽车充电需求的不确定性，提出一种面向主动配电网的两阶段鲁棒优化模型，但所考虑的柔性负荷类型较为单一。

在此背景下，为提高配电网运行优化的计算效率，提出一种考虑光伏发电、风力发电与柔性负荷的ADN 运行优化模型，并对模型进行线性化处理。首先，以系统购电成本和分布式发电运行成本之和最小化为目标，构建ADN 的运行优化模型；其次，分别对分布式发电以及柔性负荷进行数学建模；最后，为了提高计算效率，采用分段线性化方法将所提模型转换为混合整数线性规划（mixed integer linear programming，MILP）问题。

1 计及线性化潮流约束的ADN 运行优化模型

1.1 目标函数

以运行周期内ADN 总的运行成本F最小为目标函数，具体包括系统购电成本、风电机组发电运行成本和光伏机组发电运行成本。

式中：T为时段数；NG为与主网连接的变电站节点数；NMT、NPV和NWT分别为燃气轮机、光伏发电机组和风力发电机组的设备数目；为场景s下时段t燃气轮机m的运行维护成本；为场景s下时段t光伏机组p的运行维护成本；为场景s下时段t风电机组w的运行维护成本；为场景s下时段t由变电站节点k购电的成本。

其中，场景s下时段t从变电站节点购电的成本表示为

式中：Pk,t,s为主电网在场景s下时段t向节点k注入的有功功率；ρk为主电网向节点k供电的成本系数。

其中，燃气轮机的二次成本函数描述为

式中：am、bm、cm为二次成本系数；Pm,t,s为场景s下时段t燃气轮机m的输出功率。

其中，光伏发电与风力发电的成本函数分别表示为式（4）和式（5）。

式中：Pp,t,s为光伏阵列的输出功率；Kp为光伏发电的成本系数；Pw,t,s为风电机组输出的有功功率；Kw,t,s为风电机组的成本系数。

1.2 柔性负荷约束

在主动配电网中，柔性负荷可以根据系统调控的需要［22］，通过需求侧管理等措施灵活调节其负荷功率，柔性负荷的约束如式（6）和式（7）所示。

1.3 功率平衡约束

功率平衡约束包括节点有功功率和无功功率平衡约束，即：

式中：ΨMT、ΨPV和ΨWT分别为燃气轮机、光伏发电和风力发电的节点集合；ΨD为负荷的节点集合；Pl,t,s为在场景s下时段t线路l的有功功率；Ql,t,s为在场景s下时段t线路l的无功功率；Pn,t,s为主电网在场景s下时段t向节点n注入的有功功率；Qn,t,s为主电网在场景s下时段t向节点n注入的无功功率；Qm,t,s为在场景s下时段t燃气轮机输出的无功功率；Qp,t,s为在场景s下时段t光伏机组输出的无功功率；Qw,t,s为在场景s下时段t风电机组输出的无功功率；Qn,t,s,d为在场景s下时段t节点n处负荷的无功功率需求；z(l)为线路l的首端节点；r(l)为线路l的末端节点；Yl为线路l的导纳；αn,t,s为在场景s下时段t节点n的电压相角；αz(l),r(l),s为在场景s下z(l)和r(l)节点的电压相角差；Vz(l),t,s和Vr(l),t,s分别为在场景s下时段t节点z(l)和r(l) 处电压；l∶z(l)=n表示线路l始端节点为z(l)；l∶r(l)=n表示线路l末端节点为r(l)。Pl,t,s(Vz(l),t,s,Vr(l),t,s,Yl,αz(l),r(l),s)表示在时段t场景s下由节点z(l)和r(l)的电压与相角差及其线路l的导纳计算的支路l功率。

1.4 安全运行约束

安全运行约束主要包括变电站输出功率约束、燃气轮机容量约束、线路容量约束和节点电压约束，即：

2 潮流约束线性化

由于配电网中潮流方程形式多样，对不同的非线性潮流方程，其线性化推导过程主要因独立变量的选择以及原始交流潮流方程的不同形式造成差异。文中提出一种更精确的配电网交流潮流线性化通式，利用该推导通式，对不同交流潮流方程进行线性处理。

根据原始交流潮流方程，可将配电网中非线性潮流方程分为节点注入电流方程、节点注入功率方程以及支路功率方程3 类。配电网节点电压幅值一般接近于1 pu 且输电线路两端电压相角差非常小，接近于0°。文中采用线性化方法计及节点电压偏差，且对输电线路两端电压相角差进行考虑，通过分析得到交流潮流方程式（18）和式（19），其中非线性项表示为独立变量θl,t,s和γl,t,s的三角函数，故对非线性三角函数进行线性化处理，即可得到线性化潮流方程的通式。综上，对交流潮流方程进行线性化处理可以在保证计算精度的前提下，显著提高模型计算效率，使模型能应用于大规模的电力系统［23-24］。非线性潮流约束包括线路的有功潮流方程和无功潮流方程，即：

式中：Gl为线路l的电导；Bl为线路l的电纳；Vz(l)和Vr(l)分别为节点z(l)和r(l)的电压。

为线性化处理上述方程，首先将节点电压表示为

式中：ΔVn,t,s为场景s下节点n在时段t的电压偏差。

由于正常运行时，节点电压的偏差值不大，可以将其近似表示为

然后，将式（16）、式（17）代入式（14）和式（15）可得式（18）和式（19）。

式中：γl,t,s为时段t场景s下节点z(l) 和节点r(l) 的相角差；θl,t,s为时段t场景s下节点z(l)和节点r(l)的电压偏差与相角差的和。

对非线性方程进一步采用分段线性化方法，对上式中的三角函数进行近似处理，设定正弦函数sinx和线性函数(mx+e)，其中m和e为正弦函数sinx线性化过程中线性函数系数，令

图1（a）中直线即为正弦函数sinx的最佳替代线。

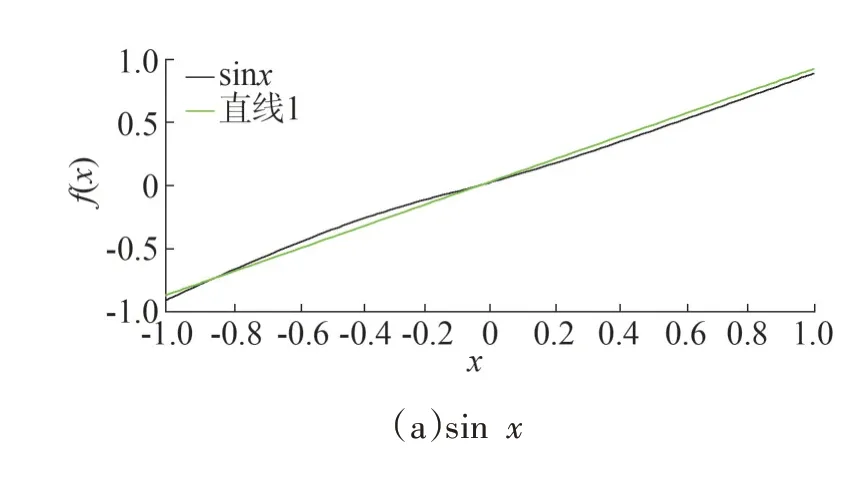
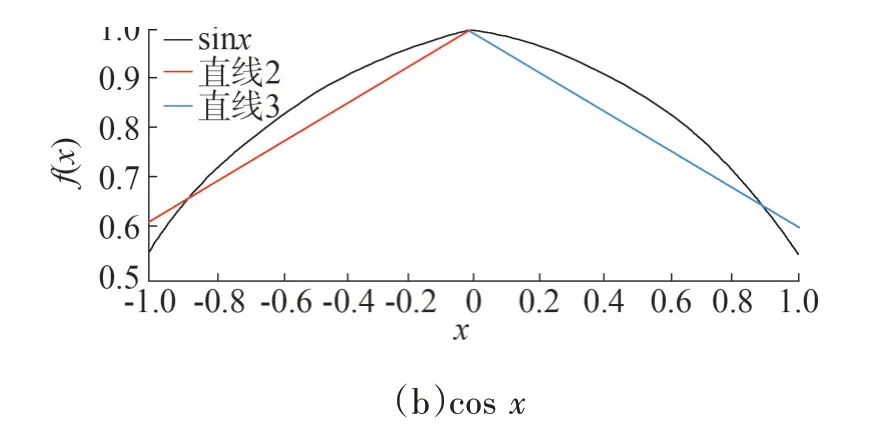
图1 线性函数对三角函数的近似Fig.1 Approximation of linear function to trigonumetric function

用线性函数对cosx进行近似，图1（b）表示两条线是cosx的最佳近似，具体过程为：

式中：K1—K8为辅助系数；w1，w2为辅助二进制变量；Ω1和Ω2为线性过程线性函数与二进制变量（w1，w2）乘积的简化表示；m1、m2、m3、e1、e2、e3为cosx函数线性化过程中线性函数系数。

当-1≤x≤1 时，cosx应该用两条线直线近似，如式（24）所示。式（24）是二进制变量（w1，w2）与另一个变量的乘积，所以是非线性的。为了处理这种非线性式，令约束式（24）中的第一项和第二项分别等于Ω1和Ω2，并添加约束式（25）—式（33）。式（25）中表示的二进制变量w1和w2是互斥的。若w1=1，式（26）和式（27）中Ω1≥-K1，Ω1≤K2，根据式（28）和式（29），Ω1=m2x+e2，由于w2=0，根据式（30）和式（31），Ω2=0，约束式（32）和式（33）是无效的，其中K7和K8为大数。在式（30）和式（31）中，如果w2=1，则Ω2≥-K5，Ω2≤K6，根据式（32）和式（33），Ω2=m3x+e3，而w1=0，根据式（26）和式（27），Ω1=0，约束式（28）和式（29）是无效的，其中K3和K4为大数。

图1（b）表示两条直线是cosx的最佳近似线段，其中m2=0.4，e2=1，m3=-0.4，e3=1。cosx的两条直线之间的最大差值是0.081 1，小于任何其他可能直线的最大差值。为使非线性约束式（10）—式（12）转变为线性约束，将其改写为

式中：P为有功功率；Smax为视在功率最大值；cosφ为功率因数。

同样，对式（34）中的余弦项进行线性化处理表示，可得式（35）。

通过上述线性化方法，可将ADN 的运行优化模型转化为混合整数线性规划MILP 模型，从而采用线性求解器直接求解获取最优解。

3 算例分析

为了验证所提主动配电网运行优化模型的有效性与可行性，分别采用改进的IEEE 33 节点和IEEE 69 节点测试系统进行分析计算。计算机配置为Intel Core i7 处理器、8GB RAM，并通过CPLEX 求解器进行优化计算。

3.1 IEEE 33节点配电网

图2 为IEEE 33 节点配电网的接线系统图。在节点8、节点13、节点16 和节点25 上安装有微型燃气轮机，光伏发电和风电分别安装在节点18 和节点33，额定参数如表1 所示。各DG 的成本系数、线路参数及负荷数据参见文献［25-26］。设分布式电源和负荷的预测误差满足均值为0、方差为0.2 的正态分布。

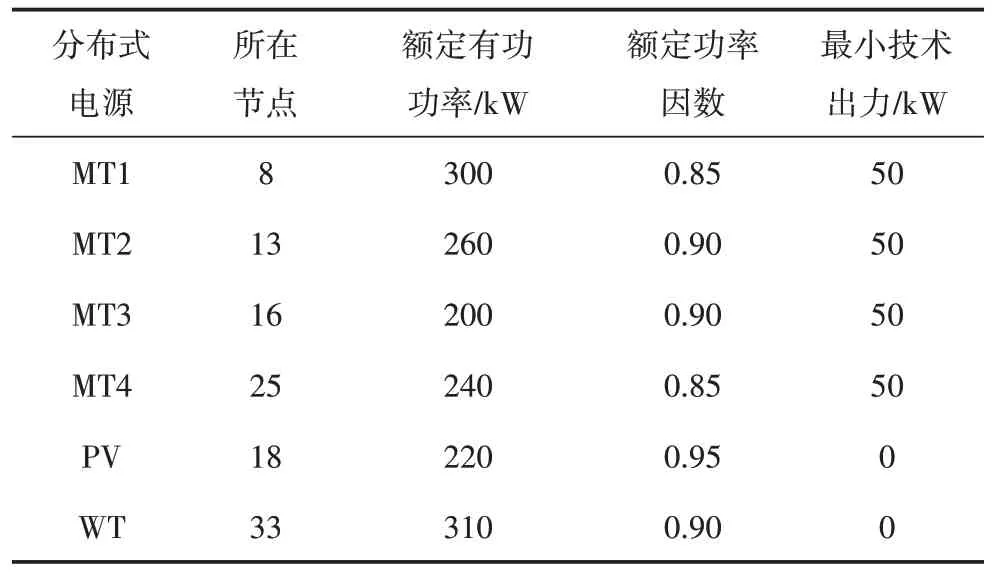
表1 分布式电源的参数Table 1 Parameters of distributed generation

图2 IEEE 33节点配电网测试系统Fig.2 IEEE 33-bus distribution network testing system

设各节点柔性负荷的参与度为20%，向上调整系数和向下调整系数均为0.3。线性化潮流约束下的运行成本计算结果如图3 所示。由图3 可以看出，随着负荷的逐渐增加，特别是在13：00—19：00的负荷高峰时段批发电价较高，运行成本增加。各节点电压幅度的波动范围为0.95～1.05 pu。将光伏机组和风电机组退出运行，在无REGs 出力的情况下系统总运行成本为21 637.92 美元，而在接入REGs 的情况下总运行成本为19 064.17 美元，下降了约11.89%。图4 为REGs 接入前后各时段由主网注入的有功功率对比情况。由图4 可见，通过将REGs 接入到配电网中进行发电，减少了由主电网注入配电网的有功功率，提高了运行的经济性。

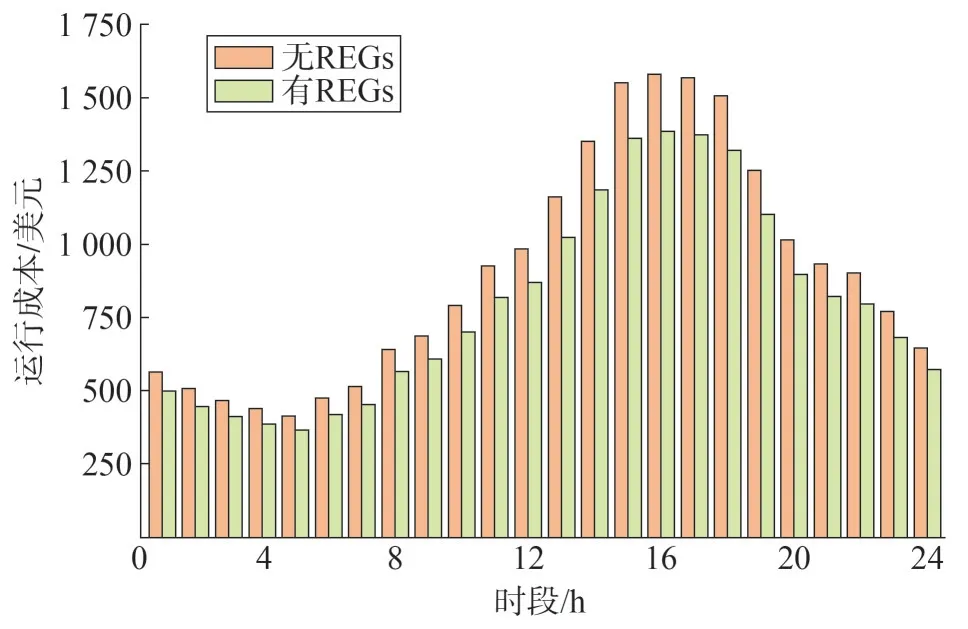
图3 各时段运行成本Fig.3 Operating cost during each time period

图4 主电网注入有功功率Fig.4 Active power injected into the main power grid

图5 为各燃气轮机的出力分布情况，在22：00 至10：00 期间，由于负荷需求和电价较低，主要由主网提供电能，燃气轮机维持在最小的技术出力水平。在11：00 至14：00 期间，随着负荷需求的逐渐增加和主电网购电成本的逐渐上升，各燃气轮机逐步加大出力，由于MT1 和MT4 的成本系数相对较小，其功率占比相对较大，出力较多。在15：00 至18：00 的负荷高峰期，各燃气轮机的输出功率接近于额定值。

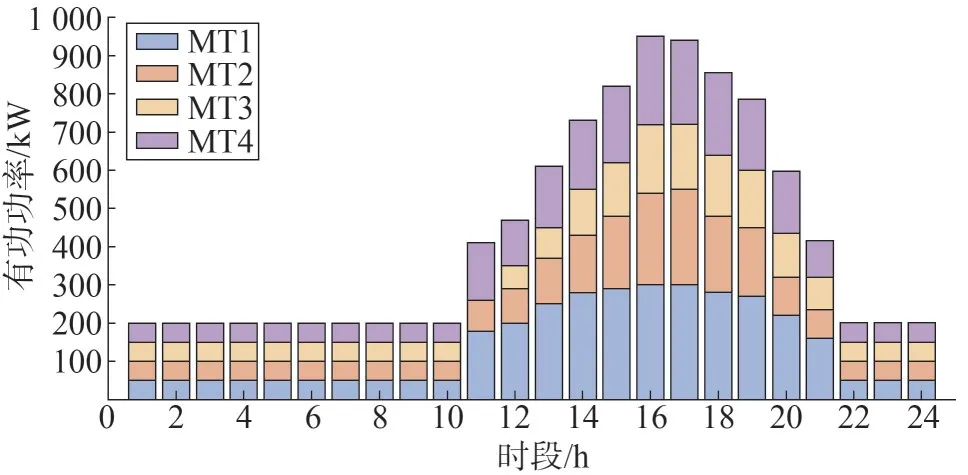
图5 燃气轮机的机组出力Fig.5 Output of gas turbine

图6 为线性和非线性模型下有无光伏情况时燃气轮机的出力对比情况，从图中可以看出光伏的影响。在22：00 至10：00 期间，由于负荷需求和电价较低，四种场景的燃气轮机均维持在最小的技术出力水平。在一天的另外12 小时，例如在12：00 时，线性模型中有光伏的场景比无光伏的场景功率输出降低约为7.2%，非线性模型中有光伏的场景比无光伏的场景功率输出降低约为6.0%，表明光伏可以有效减少燃气轮机的出力，应对增加的负荷需求，提升系统经济性，且线性模型较非线性模型计算结果偏差不大。

图6 不同场景燃气轮机的机组出力Fig.6 Unit output of gas turbines under different scenarios

图7 为模型线性化前后末端节点33 的电压对比情况。经过运行优化，节点电压水平均维持在0.95 pu 以上，线性化模型得到的电压分布与非线性模型非常相近，误差控制在1%以内，所以对非线性方程的线性化处理是可行的。

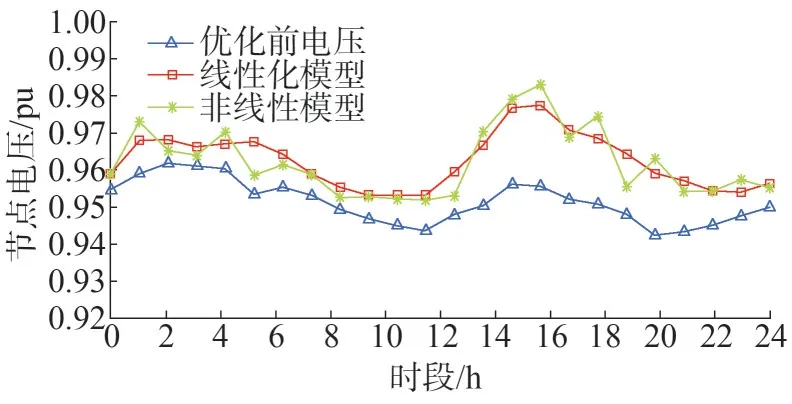
图7 线性化前后33节点的电压Fig.7 Voltage of 33 node system before and after linearization

为分析柔性负荷对配电网运行优化的影响，分别设置10%、20%、30%和50%四种柔性负荷的参与度。图8 给出了不同参与度下日负荷曲线的变化对比情况。由图8 曲线看出，随着各节点柔性负荷占比的逐渐增加，负荷峰谷差减小，负荷曲线逐步趋向于平坦，说明柔性负荷参与配电网运行优化后可以起到削峰填谷的作用，平滑负荷曲线。

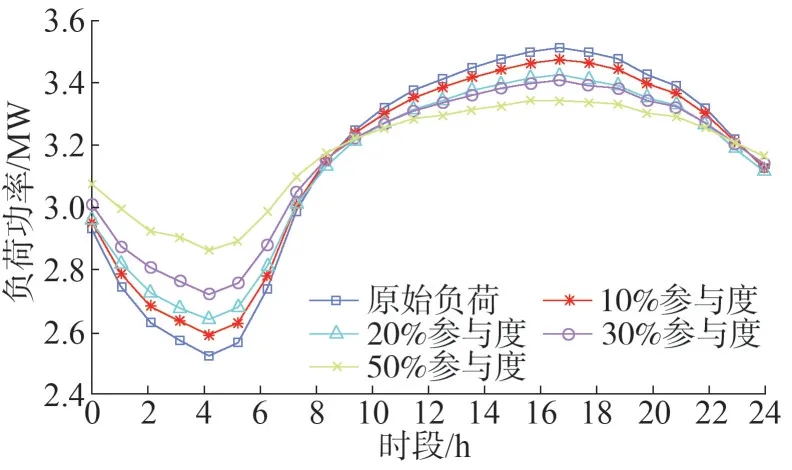
图8 柔性负荷参与后的日负荷曲线图Fig.8 Daily load curve after flexible load participation

为分析柔性负荷对配电网运行优化的影响，表2给出0、10%、20%、30%和50%五种柔性负荷参与度下系统的运行成本和最低节点电压的对比情况。由表2 可知，随着柔性负荷占比的提高，配电网运行成本逐步降低，而最低节点电压则逐步提升，说明柔性负荷可以有效提高系统运行的经济性和节点电压水平。

表2 不同柔性负荷参与度下的运行指标Table 2 Operational indicators under different levels of flexible load participation

3.2 IEEE 69节点配电网

为了进一步验证线性化方法与所提模型的有效性及可行性，进一步采用IEEE 69 节点配电网进行测试分析。IEEE 69 节点配电网的原始参数和负荷分布参考文献［27-28］。在节点8、节点33 和节点61 上分别接有额定容量0.3 MW 的光伏电源，柔性负荷的参数设置同IEEE 33 节点系统。图9 为IEEE 69 节点系统中6 个典型场景的负荷曲线。

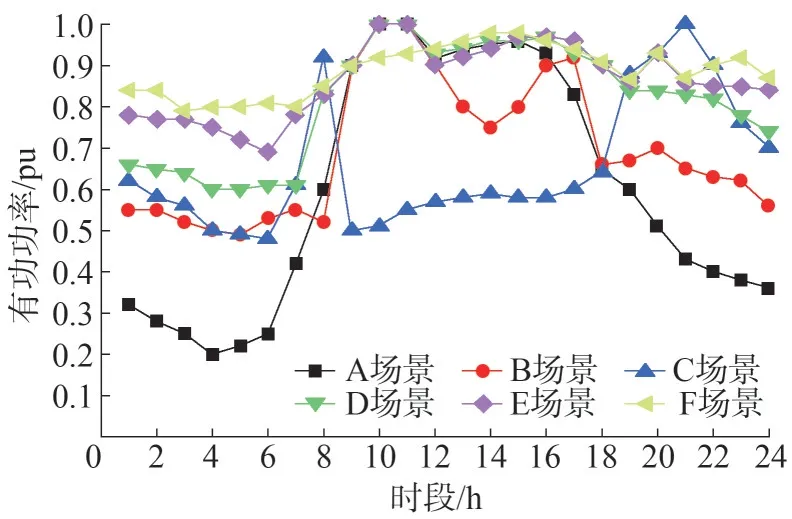
图9 IEEE 69节点系统日负荷曲线Fig.9 Daily load curve in IEEE 69-bus system

为进一步分析线性化处理对模型的影响，对IEEE 69 节点系统进行分析计算。IEEE 69 节点系统的线性模型和非线性模型的计算结果如表3 所示。线性模型和非线性模型的总运行成本分别为19 671.058 美元和20 105.097 美元，由于计算所依据理论公式本身的近似性，或实验条件不能达到理论公式所规定的要求，使各时段的成本误差控制在8%以内，进一步表明所采取的线性化处理手段是有效可行的，计算结果接近于非线性模型。

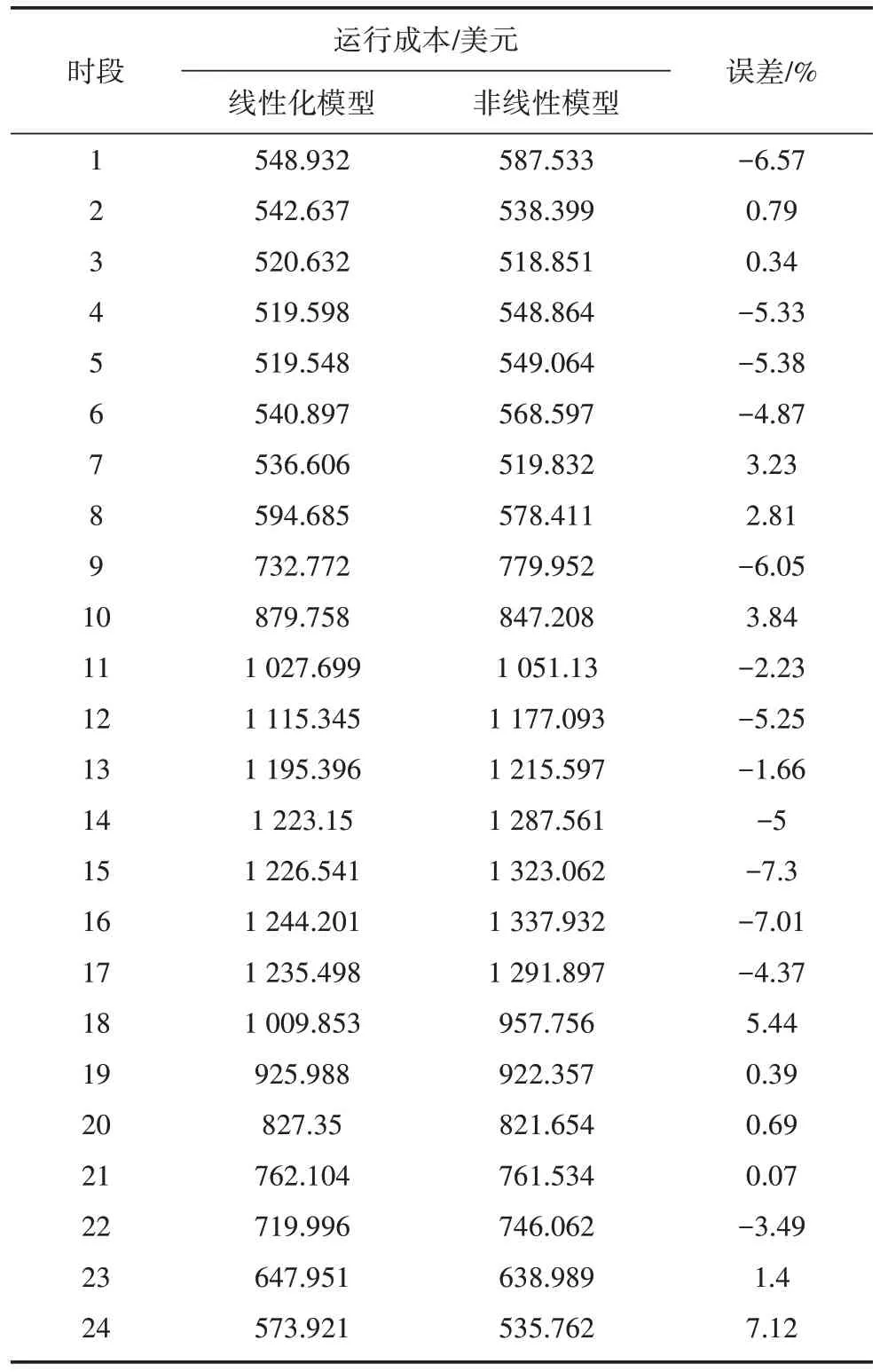
表3 线性化问题的小时成本和总成本计算结果Table 3 Calculation results of hourly and total costs for linearization problems

为分析模型的计算时间，IEEE 33 节点和IEEE 69 节点系统的优化计算时间如表4 所示。IEEE 33节点和IEEE 69 节点系统的非线性模型的计算时间分别为1 216 s 和3 589 s，而线性化模型的计算时间分别为107 s 和268 s，耗时减少90%以上。结果表明，模型线性化后在保持计算精度的同时，显著提高了求解效率，缩短了模型计算时间。