考虑双重柔性的空间机器人动力学建模与仿真

张青云

（天津财经大学珠江学院 数据工程学院，天津 301811）

近年来，空间机器人协同办公在分拣物品、精密仪器组装以及航天领域引起了极大关注，对其机械特性、振动特性及控制策略进行分析已成为空间技术发展的重要领域之一[1-3]。基于高速化和高精度化发展需求，空间机器人各构件逐步轻质化，使得空间机器人柔性特性愈发凸显，为了进一步了解含柔性变形的空间机器人性能，对其进行动力学分析必不可少[4-6]。目前，空间机器人柔性性能分析主要集中在空间串联机械臂和空间双臂机器人[7-8]。但由于其累计误差较大，承载力较小等，应用范围存在一定局限性。因此，采用空间并联机器人进行高速高精度协同办公的领域越来越多，该系统结合了柔性关节间隙及摩擦力小和并联机构刚度大及结构稳定等优点，使其在精密测量、医疗微操作等领域具有巨大作用[9]。虽然空间并联机器人提高了系统自由度和运动精度，但在高速操作下连杆柔性引起的重力变形、刚性连杆和柔性连杆之间的耦合变形以及柔性连杆和柔性铰链之间的耦合变形将影响系统稳定性和轨迹跟踪精度[10-11]。部分学者针对机器人中构件细长比大于20 的构件进行柔性分析，结果表明其产生的弹性变形将引起末端执行机构产生微小位移，降低轨迹跟踪精度；还有些学者研究关节柔性对机器人动力学性能的影响，发现合理利用其动力学模型，可提高机器人被动顺应能力，减少间隙振动，从而提高机器人使用寿命[12-15]。

现阶段，在分析空间并联机器人动力学特性时，一般先研究其中一条运动支链动力学模型，再根据运动支链之间的位姿关系获得其余运动支链动力学方程，将其进行组装即可构成空间并联机器人动力学方程。为了简化分析，大多数运动支链都是平面串联机构，刚度矩阵为常数矩阵，忽略了柔性变形对刚度矩阵的影响[16-18]。为了分析关节柔性、连杆柔性及刚柔耦合特性对空间机器人动力学特性的影响，将3-RRRU 空间并联机器人作为研究对象，考虑在柔性关节和柔性空间连杆双重柔性作用下的机器人动力学特性，并分析不同关节材料对系统固有频率的影响、关节接触力变化特性及柔性变形对末端执行器运动轨迹的影响。

1 物理模型

为实现生产过程中的高速高精度轨迹跟踪控制，通常使用轻型空间并联机器人辅助货物分拣、精密仪器组装等任务。鉴于轻型结构在运动过程中将产生弹性变形，因此，通过对存在关节柔性和连杆柔性的3-RRRU 空间并联机器人进行动力学分析，其结构简图如图1 所示。

图1 3-RRRU 双重柔性空间机器人Fig.1 3-RRRU dual flexible spatial robot

其中，固定平台与机架固定，并通过转动副与3 条运动支链相连。运动支链之间夹角都为120°，且每条运动支链均由3 个连杆（主动杆、中间杆和从动杆）通过转动副连接而成。其中，主动杆和中间杆在绝对坐标系下绕x轴运动，从动杆绕y轴转动。末端执行器则通过虎克铰与从动杆进行连接。

1.1 柔性空间连杆模型

由于从动杆为圆形横截面细长连杆，运动过程中产生的弹性变形不可忽略，因此，采用简支梁模型进行简化，再用有限元法将其离散，并根据浮动坐标系法描述位移场矢量。由于关节柔性也需进行动力学建模，则在从动杆模型中不再引入额外自由度，避免因自由度重复导致模型错误等问题。柔化过程如下：

1）采用SOLODWORKS 软件建立从动杆3D模型，且存为“x_t”格式。

2）将3D 模型导入商品化仿真软件，并添加物理属性，如表1 所示。

3）由于从动杆结构简单，直接采用商品化仿真软件中的柔性模块即可对构件进行柔化处理。

为了突出显示从动杆在刚性条件和柔性条件下的区别，其模型对比如图2 所示。

图2 柔性空间连杆模型Fig.2 Flexible spatial link model

1.2 柔性关节模型

从动杆变形将引起末端执行器产生微小位移，因此，将从动杆与末端执行器之间的虎克铰视作柔性关节将更符合实际。为了研究柔性关节性能，一般将其简化为具有恒定刚度的线性扭转弹簧[19]，并对其连接方法进行如下假设：

1）使用柔性关节作为柔性空间连杆的弹性约束。

2） 将柔性空间连杆和柔性关节简化为具有单向弹性约束的两个柔性构件和一个简支梁的双重柔性模型。

3） 柔性关节与刚性连杆的连接采用刚性约束连接。

由于柔性虎克铰能够提供二维转动，为了简化分析，将其横截面设为圆形。其中，外圈1 和外圈2都由两组“Y”型弹簧片构成，分别沿x、z轴转动[20]。因此，空间机器人转动过程中，虎克铰直线簧片将存在微小弹性转动，曲线簧片存在微小弯曲转角，关节模型如图3 所示。

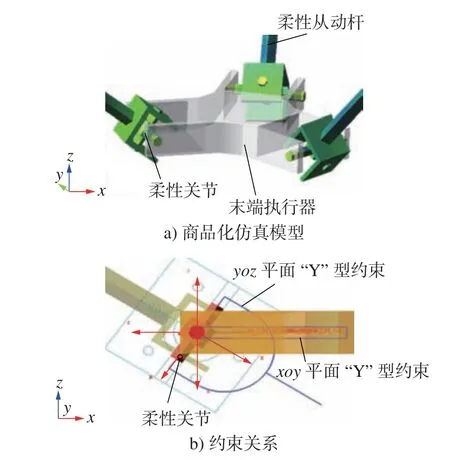
图3 柔性虎克铰模型Fig.3 Flexible hooke hinge model

1.3 双重柔性空间机器人模型

将柔性关节、柔性空间连杆、刚性主动杆和刚性中间杆相连即可获得系统运动支链模型，如图4a）所示。其中，ai-xaiyaizai为主动杆局部坐标系，与全局坐标系3 个坐标轴方向一致；bi-xaiyaizai和ci-xciycizci分别为中间杆和从动杆坐标系。由于全局坐标系下柔性空间连杆转动轴线和刚性连杆转动轴线不一样，使得运动支链为空间机构，增加建模难度，影响系统动力学特性。为显示柔性变形对空间机器人的影响，其与刚性状态下的空间机器人对比图如图4b）所示。

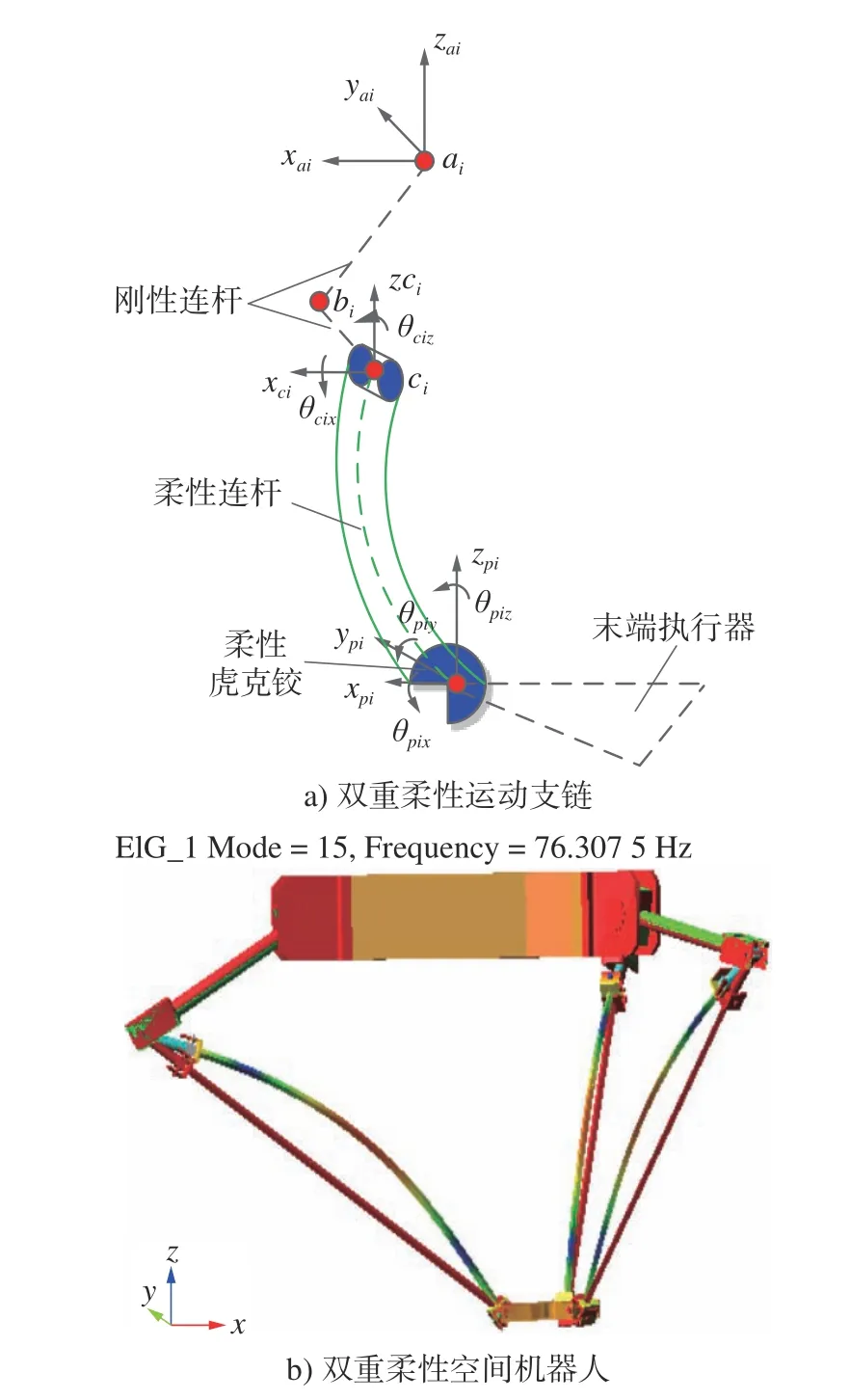
图4 双重柔性空间机器人模型Fig.4 Dual flexible spatial robot model

2 动力学建模

2.1 柔性关节动力学建模

根据图3 可知，柔性关节两端存在微小转角θjoint-j（j=1, 2），根据动能定理即可获得柔性关节动能和势能分别为：

式中：θjoint和Jjoint分别为柔性关节转角矩阵及转动惯量矩阵，θjoint=和Jjoint=；Kjoint为柔性关节扭转刚度，Kjoint=；ωjoint为柔性关节角速度，根据绝对转角与中间变量z的关系即可求出，具体表达式为

将式（1）代入第一类拉格朗日方程即可获得柔性关节动力学方程组为

式中τjoint为柔性关节输出力矩。

为了简化分析，在转动中心绕轴x进行转动时，只计入铰链偏转位移，而忽略刚性区域变形。因此，柔性虎克铰可用平面梁的柔度矩阵来分析，其等效刚度[21]为

式中： δ为转角位移，由直线簧片弯曲转角θjoint-1和曲线簧片变形转角θjoint-2构成。

2.2 柔性空间连杆动力学建模

根据图4 可得柔性空间连杆坐标系简图如图5所示。

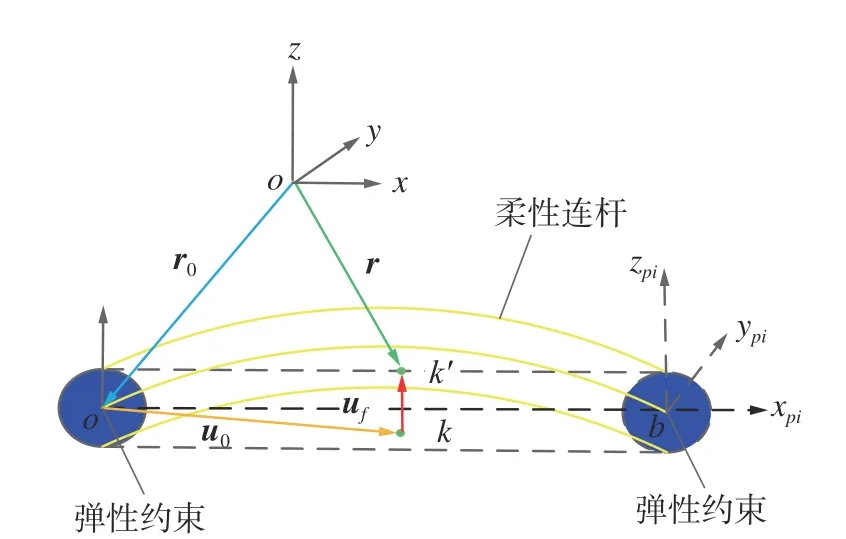
图5 柔性空间连杆坐标系简图Fig.5 Coordinate system of flexible spatial link

在全局坐标系o-xyz下，采用浮动坐标系法即可描述构件上任意一点k的位移场矢量。为了逼近构件变形对系统动态性能的影响，通过有限元法将构件离散为有限维梁单元， 并根据多项式法对梁单元形函数N进行表示，则

式中：梁单元横向位移Nx和Ny用一次插值函数描述，轴向位移Nz用三次插值函数表示。

柔性空间连杆任一点k坐标可表示为

式中：r0为柔性空间连杆坐标系原点在全局坐标下的位移场矢量；T为柔性空间连杆坐标系变换到全局坐标系下的旋转矩阵；u0和uf为柔性空间连杆变形前和变形后的坐标矢量，uf=Nqf，qf为梁单元广义坐标。

根据动能公式可得柔性空间连杆动能[22]为

式中： ρ为柔性空间连杆密度；Jc为转动惯量；lcipi为长度。

柔性空间连杆势能[22]为

式中：A为柔性空间连杆横截面面积；E和G分别为弹性模量和剪切模量；Iyy和Izz分别为横截面对y轴和z轴的惯性矩函数；Ip为横截面对x轴的极惯性矩函数； ψx为柔性空间连杆绕x轴的弹性转角函数。

2.3 刚性连杆动力学建模

根据运动支链坐标系图4a）可知全局坐标系下主动杆和中间杆的位移矢量，再根据动能定理可推导出其动能[22]表达式为：

式中：laibi、lbici、lcipi分别为主动杆、从动杆和柔性空间连杆长度；maibi、mbici、mcipi分别为主动杆、从动杆和柔性连杆质量。

同理，主动杆和中间杆的势能[22]表达式为：

柔性空间连杆的变形运动将引起末端执行器位移和转角产生微小移动。因此，通过协调矩阵[23]描述末端执行器微小位移，具体表达式为：

式中：mp为末端执行器质量；p为末端执行器在全局坐标系下的位移矢量；Jp为协调矩阵；wp为末端执行器绝对角速度。

2.4 双重柔性空间机器人动力学建模

将刚性构件、柔性关节和柔性空间连杆的动能和势能进行组装即可获得运动支链动能和势能，再将其带入第一类拉格朗日方程，可得

式中：M为支链质量矩阵；K为支链刚度矩阵；C为系统约束方程；Q为广义力。

由于运动支链之间的夹角为120°，将运动支链动力学一般方程通过位姿变换即可求出其余两条运动支链动力学方程。再与末端执行器动力学方程进行组装即可获得双重柔性空间机器人动力学方程。

3 仿真校验

为了验证仿真模型图4 正确性，可先对模型约束关系进行验证，其结果如图6 所示。

图6 双重柔性空间机器人商品化仿真模型
Fig.6 Commercialization simulation model for dual flexible spatial robot

由图6 可知：模型自由度与理论计算一致，说明模型约束关系正确。通过商品化仿真软件中GSTIFF 积分器、SI2 积分格式对双重柔性空间机器人动力学进行仿真。其中，空间机器人主要用于装配现场，其构件尺寸符合常规工业机器人需求，具体几何参数如表1 所示。

为验证动力学运动正确性，基于全局坐标系对双重柔性空间机器人z方向施加重力场，并将MATLAB 逆动力学数值运算结果加载到3 个主动构件，使得末端执行器在局部坐标系xoy平面做圆形运动，其空间轨迹对比结果如图7 所示。

图7 末端执行器空间轨迹Fig.7 End effector spatial trajectory

根据图7 可得：在柔性关节和柔性空间连杆变形影响下，末端执行器运动轨迹产生振动。为了更直观看到本文数值模型和商品化软件仿真模型的结果，将运动轨迹分别投影到3 个坐标轴，则其偏差结果如表2 所示。

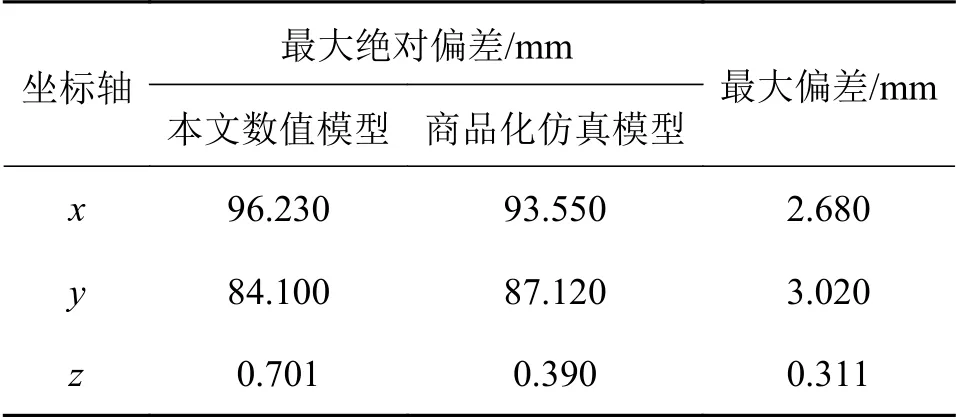
表2 运动轨迹偏差Tab.2 Motion trajectory deviation

根据表2 结果可知：本文数值模型和商品化仿真模型运动趋势基本一致，由于商品化仿真模型及既考虑了关节柔性，又考虑连杆柔性，其在运动过程中会减少间隙对末端轨迹的影响，因此，其数值波动范围小于本文数值模型。其中，z方向的偏差范围为0 ～ 0.311 mm，x方向的偏差范围为0 ～ 2.68 mm，y方向的偏差为0 ～ 3.02 mm。由此可知，商品化仿真模型在一定程度上能反应数值模型特性，通过商品化仿真模型进行动态性能分析以及控制策略研究具有可靠性，且便于模型参数修改，提高分析效率。

3.1 不同关节材料对系统固有频率影响

柔性关节可降低构件之间的摩擦、减少装配间隙，提高设备运动精度等。不同关节材料对系统固有频率影响不同，因此，分别采用铝合金、钢、铜作为柔性关节材料，分析3 个阶次模态固有频率的变化值如表3 所示。

表3 柔性关节材料对系统固有频率的影响Tab.3 The influence of flexible joint materials on the natural frequency of the system

由表3 可知：同一阶次下不同材料对应不同固有频率，其中弹性模量越大、刚性越强，其固有频率越低。图8 为3 组固有频率变形。

图8 固有频率对比图Fig.8 Comparison of natural frequencies

通过分析固有频率变化，可得到系统危险点，再根据危险点与激励源对比即可求出共振点位置，为优化系统性能提供分析基础。综合表3 和图9 可知：随着关节弹性模量增大，构件刚度增强，固有频率随之变大，导致装配间隙减少，冲击力变大。其中，刚性关节引起变形最小，铜次之，铝合金最大。与此同时，柔性连杆中心点和柔性关节连接点变形最大，应对其进行优化，提供系统振动性能。

图9 不同弹性模量下关节接触力Fig.9 Joint contact force under different elastic moduli

3.2 不同关节材料接触力分析

基于柔性从动杆条件下，虎克铰在刚性和柔性情况下的接触力随时间的变化如图9 所示。

由图9 可知：3 条运动支链从动杆柔性状态下的接触力在开始阶段大于刚性状态，但随着时间推移，通过关节柔性变形，将减少关节间隙，其接触力得到部分抵消。因此，处于基本平稳状态下时，柔性关节接触力将小于刚性关节。通过合理选用关节材料，利用柔性变形特性，可减少关节冲击力，提高系统使用寿命。

4 结论

对含柔性连杆和柔性关节的双重柔性空间机器人动力学特性分析可知：

1） 柔性关节和柔性连杆在运动过程中产生的弹性变形对系统末端执行器运动轨迹具有重要影响。因此，建立精确空间机器人动力学模型时，其构件和关节柔性不可忽略。

2） 系统运行过程中，柔性关节与刚性连杆、柔性关节与柔性空间连杆之间的耦合效应十分复杂，考虑高阶模态才能反应耦合效应对系统运动轨迹的影响。

3） 不同材料对柔性变形影响不同，随着其弹性模量增加，刚度增大，装配间隙减少，振动冲击力随之增加，通过合理选择材料可改善系统振动性能，提高系统使用寿命。

4） 商品化仿真模型约束关系及动力学运动性能与本文数值模型相一致，因此，通过商品化仿真模型研究双重柔性空间机器人动力学特性及控制策略具有科学性。