室外换热器可变流路设计及试验分析

陶 骙，邵艳坡，吴 恒，晏 刚，肖芳斌，陈 磊，黎顺全，李健锋

（1.西安交通大学 能源与动力工程学院，西安 710049；2.广东美的制冷设备有限公司，广东佛山 528311）

0 引言

随着人们生活水平的提高，空调器已被广泛应用于家庭、工商业等领域。为了提高空调器能效，需对系统各部件进行优化。换热器优化是空调热泵系统节能提效的关键之一，VOLOSHCHUK等［1］对空调系统进行了㶲分析，结果表明，63%和20%可避免的㶲损失分别发生在蒸发器和冷凝器中。因此要提高空调器系统的性能，有必要提高换热器性能。由于空间与成本的限制，换热器常见的优化形式主要有翅片结构、间距、管径与制冷剂流路等［2-5］。其中制冷剂流路优化易于实施且不需要增加额外成本，是最经济的优化方式［6-7］。

针对制冷剂流路已进行了许多研究，张浩等［8］针对空调室外机的制冷剂从上至下沿程流动时干度逐渐减小的现象，提出了分布式流路，仿真研究发现采用2-3-4 分布式流路比采用流路数目单一的3 流路的额定制热量和低温制热量分别提升8.8% 和5.6%。ISHAQUE 等［9］提出了一种新型优化搜索算法对冷凝器进行优化，优化后的流路使部分负荷下冷凝器换热量提升了6.96%～9.87%。KWAK 等［10］基于热阻平衡法（空气侧与制冷剂侧热阻相等为优化目标）对冷凝器进行设计优化，研究发现在不同负荷下得到的最优流路并不相同，建议采用加权计算的方式得到最优流路。这在一定程度上促进了换热器性能的提升。

然而，现有流路优化研究大多只针对单一的蒸发器或冷凝器进行，实际上，对于具有制热与制冷2 种模式的空调器而言，室外换热器在制冷/制热模式下分别为冷凝器/蒸发器，而换热器作为冷凝器与蒸发器时的最优流路通常并不相同。可变流路技术（制冷与制热模式下换热器均运行在其最优流路）是解决这一矛盾点的关键技术，SIM 等［11］首次在文献中提出了可变流路的概念，目前只有ZHAO 等［12-13］对可变流路的应用进行了详细研究，在容量为1～7 kW 的空调器上取得了较好的效果，为空调换热器改进提供了新思路。

对于可变流路技术而言，确定制冷与制热模式下换热器的最优流路是关键。ZHAO 等［12］根据换热器仿真得到的不同流路的换热量大小来确定制冷与制热模式下的最优流路，实际上，确定换热器最优流路时还应当考虑换热器压降，因为压降变化会对压缩机耗功、制冷剂流量等产生影响，从而对系统性能也产生影响。有学者提出了综合考虑换热量与压降的熵产最小化法［14］与㶲分析法［15］来确定最优流路，但有研究表明这2 种方法也有所缺陷，得到的最优流路并不一定是系统性能最优的流路［16-17］。

综上所述，确定制冷与制热模式下系统性能最优的换热器流路是可变流路技术的关键与难点，为解决上述问题并拓宽可变流路技术的应用范围，本文将一种新的可变流路方式应用于16 kW 多联机空调器，建立了蒸发器/冷凝器仿真模型与整机系统仿真模型，进行耦合计算以直接得到不同流路对系统性能（COP）的影响，以确定冷凝器和蒸发器的优选流路。在此基础上，通过阀件实现了新的可变流路方式，并最终通过试验进行验证，可为相关研究人员提供参考。

1 单体换热器仿真

1.1 换热器仿真模型

采用分布参数法建立换热器仿真模型，为简化仿真模型并提高计算效率，模型中引入以下假设条件：（1）仿真模型中的换热及流动过程均为稳态过程；（2）U 型连接管、分配器及其他连接管路处的热损失忽略不计；（3）换热器管路均为水平布置，故压降模型中忽略重力产生的影响。

采用ε-NTU方法进行单元传热计算：

式中，t1，t2为流体进口与出口温度，℃；qm为流体质量流量，kg/s；c为定压比热容，J/（kg·K）；U为单元总传热系数，W/（m2·K）；A0为单元管外传热面积，m2。

基于管外传热面积的总传热系数U计算式为：

式中，Ar为单元管内传热面积，m2；din，dout分别为管内、外直径，m；λ为铜管导热系数，W/（m·K）；L为单元长度，m；ha，hr分别为空气侧与制冷剂侧传热系数，W/（m2·K）；ηa，ξ分别为翅片效率与析湿系数。

空气侧及制冷剂侧传热系数采用传热关联式计算得到，见表1。

表1 传热关联式Tab.1 Heat transfer correlation

单元压降采用式（5）计算，考虑加速压降ΔPs与摩擦压降ΔPf，忽略重力压降ΔPg：

式中，f为摩擦系数；G为制冷剂质量流速，kg/（m2·s）；ρin，ρout分别为单元内制冷剂进口与出口密度，kg/m3。

摩擦压降ΔPf分为单相流体摩擦压降与两相流体摩擦压降，单相流体的摩擦压降采用式（7）（8）计算［22］：

式中，ρave为单元内制冷剂平均密度，kg/m3；k为粗糙度。

冷凝模式下的两相流体摩擦压降采用式（9）～（11）计算［22］：

式中，fv为单相气体摩擦系数，采用式（8）计算；x为干度；ρv，ρl分别为气相和液相的密度，kg/m3；μv，μl分别为气相与液相的动力黏度，kg/（m·s）。

蒸发模式下的两相摩擦压降采用式（12）～（15）计算［23］：

式中，fl为单相液体摩擦系数，采用式（8）计算。

采用分布参数法对传热及压降进行耦合运算。在换热器仿真计算过程中，为了简化模型常假设换热器各支路流量是均匀分配的［6］，实际上各支路之间具有合并与分离的连接关系，各支路管数目不同会对制冷剂分配产生影响。因此基于压降守恒建立了换热器流量分配模型，换热器仿真模型构建详细过程及计算流程参考文献［24］，该文献中对模型进行单体测试和仿真结果的对比，结果表明冷凝工况能力偏差在±3%以内，蒸发工况能力偏差在±5%以内，计算模型具有一定准确性。

室外换热器规格参数见表2，额定制冷、额定制热、超低温制热工况的仿真输入条件见表3。本文提到的16 kW 多联机，原型机室外机为10进10出+4排过冷段的制冷剂流路，如图1所示。本文主要对室外机的分路数进行设计及研究，以得到制冷与制热模式下换热器的最优分路数目，因此设计流路时只对分路数进行改变，过冷段保持不变。

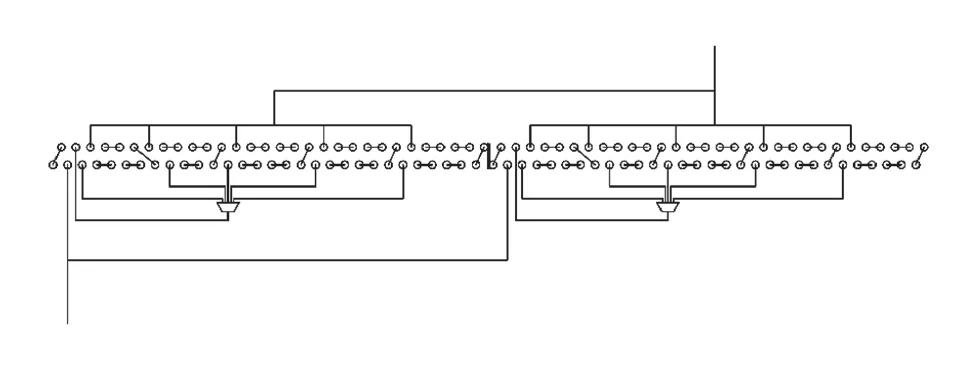
图1 原型机室外机流路Fig.1 Flow path diagram of the prototype outdoor unit

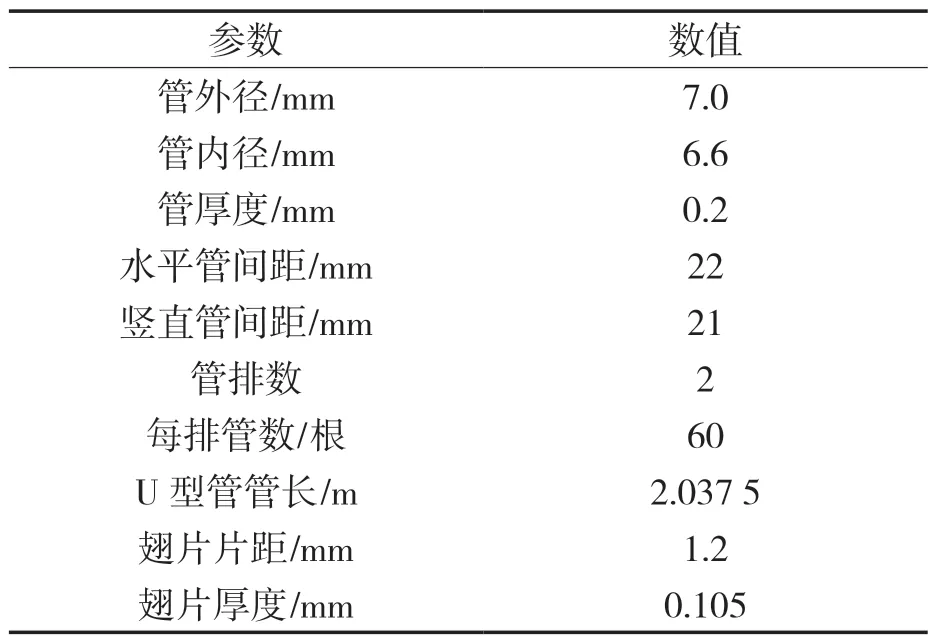
表2 室外换热器规格参数Tab.2 Specification parameters of outdoor heat exchanger

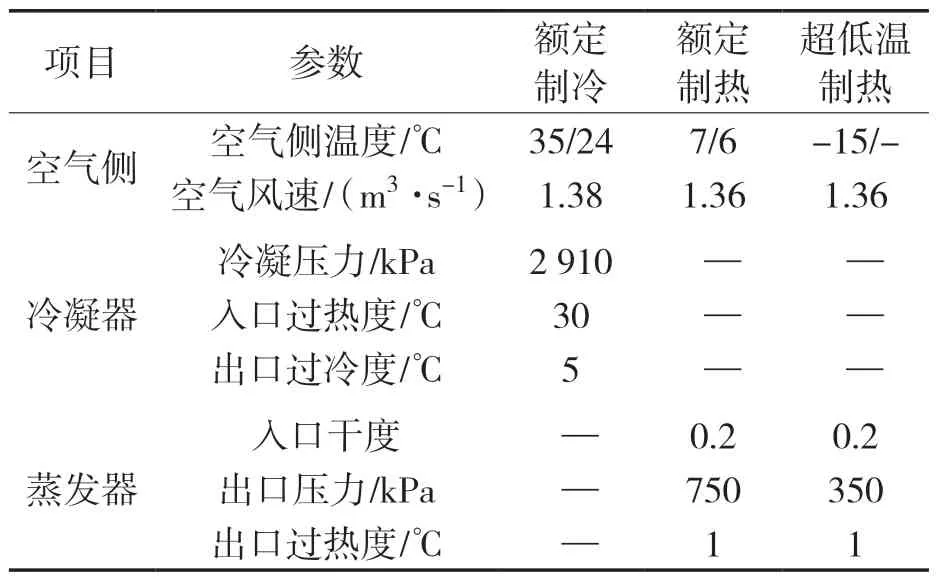
表3 仿真输入条件Tab.3 Simulation input conditions

更改室外换热器分路数时，秉承各支路蛇形管长度均匀分配的原则。这是因为空调室外机通常采用吸风的方式进行换热，换热管路上的空气流速分布相对均匀［25］，此时为了保证换热器各支路换热状态相同，要求各支路蛇形管长度相同。但由于每一路U 型管数必须为整数（1 个U 型管包括2 根换热管），有时会面临各支路管长度无法均匀分配的情况，因此设计时要求各支路U 型管数差异尽量小。以图1 中原型机室外机流路为例，将56 个U 型管分成10 路，为了尽量均匀分配只能采用每路5 个或6 个U 型管的分配方式，经简单计算可知，其中4 条支路每路5 个U 型管，另外6 条支路每路6 个U 型管。

1.2 单体换热器仿真结果讨论

图2，3 分别示出不同工况条件下室外换热器换热量及压降的变化（以原型机室外机换热量仿真结果为基准，即100%）。如图中所示，在额定制冷工况下的换热量随着分路数增大而减小，额定制热及超低温制热工况换热量随着分路数增大呈现先增加、后减小的趋势；各工况压降随着分路数增大均呈现减小趋势。

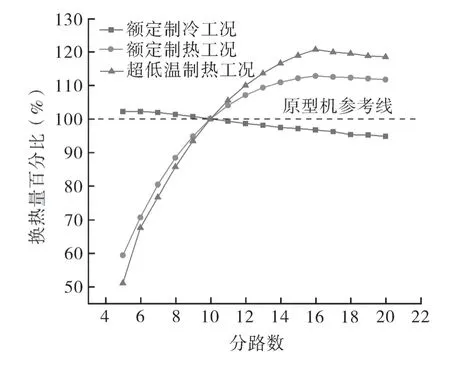
图2 单体换热器中各工况换热量随着分路数变化趋势Fig.2 Variation trend of heat transfer capacity under different operating conditions in a single heat exchanger with the number of paths

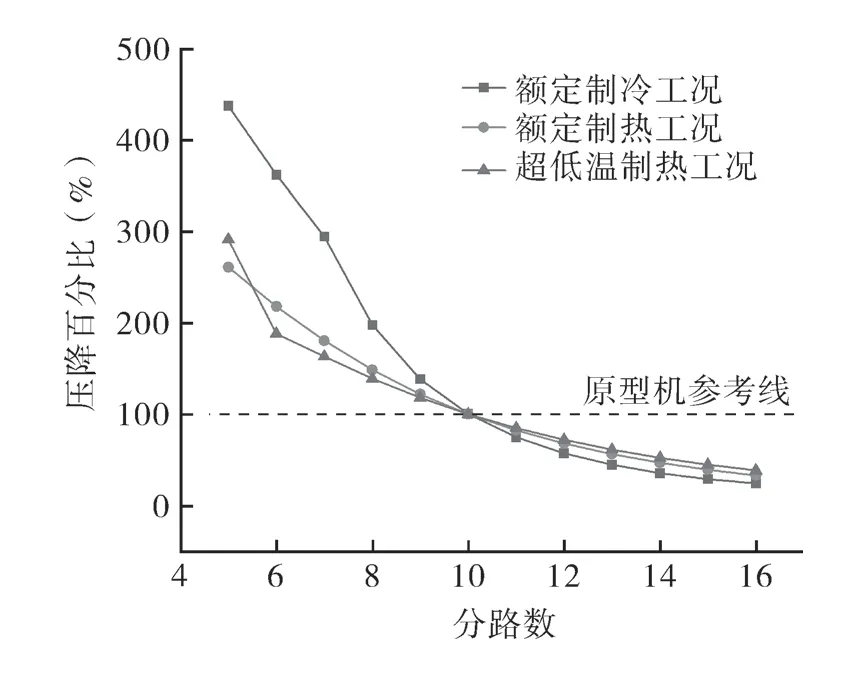
图3 单体换热器中各工况压降随着分路数变化趋势Fig.3 Variation trend of pressure drop under different operating conditions in a single heat exchanger with the number of paths

从图2，3 对比可知，将分路数从原型机的10路减小为5路时，虽然冷凝器换热量上升了2.2%，但冷凝器压降约为原型机的4.3 倍。在室外换热器中，制冷剂的压降增大将会增大系统的高低压压力差值，从而增加压缩机功耗。因此，不能通过单体换热器仿真得到的换热量大小来评判流路优劣。

根据上述分析可知，对换热器进行单体仿真只能定性分析换热量及压降变化趋势，无法确定不同流路在整机系统中的表现情况。因此，本文将换热器仿真耦合入多联机整机系统仿真中，以直接确定不同换热器流路对整机换热量及性能的影响，从而确定制冷与制热模式下换热器的优选流路。

2 整机系统仿真

将室内外换热器、压缩机、节流部件等部件连成系统，进行系统仿真。基于Modelica 语言建立了以R410A 为制冷剂的一拖四多联机空调系统动态仿真模型，将蒸发器和冷凝器仿真模型耦合入系统仿真中，压缩机和电子膨胀阀采用稳态模型，气液分离器采用集中参数动态模型，换热器模型的边界条件根据系统仿真模型计算结果动态变化。微分方程采用向后差分离散数值格式，并用基于Dymola 平台的求解器求解离散后的方程组。制冷剂物性的计算基于NIST 9.0 数据库。系统仿真模型构建详细过程及计算流程可参考文献［26］。

2.1 仿真输入条件

除室外换热器流路外，其他所有设置都一致，系统仿真输入条件见表4。

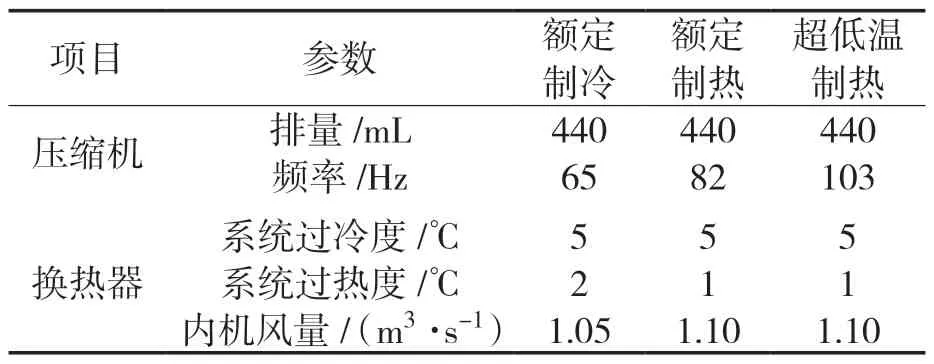
表4 系统仿真输入条件Tab.4 System simulation input conditions

2.2 不同流路下整机换热量对比

基于表3 的条件，对同压缩机频率下不同流路数的整机能力进行仿真计算，得到整机换热量计算结果如图4 所示。在额定制冷工况下，随着分路数增加，整机制冷量减小；在额定制热与超低温制热工况下，随着分路数增大，整机制热量呈现先增加、后减小的趋势。整机换热量变化与单体换热量变化趋势相近，这是室外换热器压降及平均传热系数两方面之间权衡的结果。

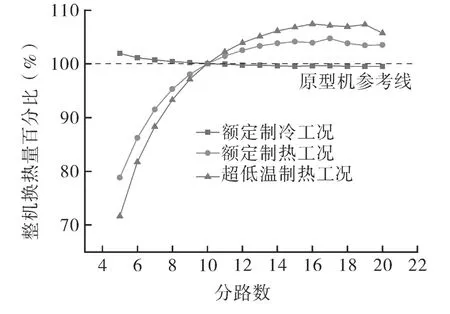
图4 各工况系统换热量随着分路数变化趋势Fig.4 Variation trend of system heat exchange capacity under various working conditions with the number of paths

图5示出不同分路数下换热器压降及平均传热系数变化情况。随着分路数增加，管内平均流速减小从而使得换热器整体压降减小，这对换热量提升是有利的，因为压降减小有助于增大换热器的平均传热温差；另一方面，随着分路数增大，管内平均流速减小，从而导致换热器制冷剂侧的平均传热系数下降，这对换热量提升是有害的。在额定制热与超低温制热工况下室外机为蒸发器，分路数较小时，压降为影响传热的主要因素，增加分路数对换热有利；分路数较大时，传热系数为影响传热的主要因素，增加分路数对换热不利。在额定制冷工况下室外机为冷凝器，对冷凝器而言其本身压降较小，此时传热系数为影响换热量的主要因素，分路数增加导致平均流速减小，从而引起传热系数下降，整机制冷量下降。

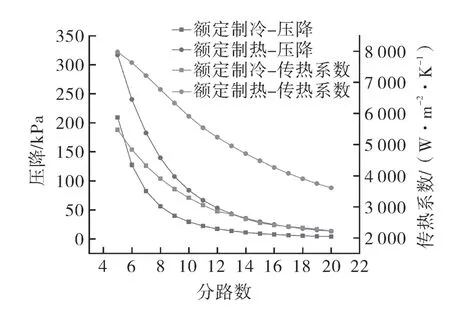
图5 压降及制冷剂侧传热系数随着分路数变化趋势Fig.5 Variation trend of pressure drop and refrigerant-side heat transfer coefficient with number of paths

2.3 不同流路数下整机能效对比

由于测试APF对能力大小有要求，改变流路的同时，通过压缩机频率来保证能力不变，再比较整机能效变化情况才具有实际意义。

基于表3 的条件（为保证能力相同，压缩机频率会变化），对不同流路数的能效进行仿真计算，得到整机能效计算结果如图6 所示。

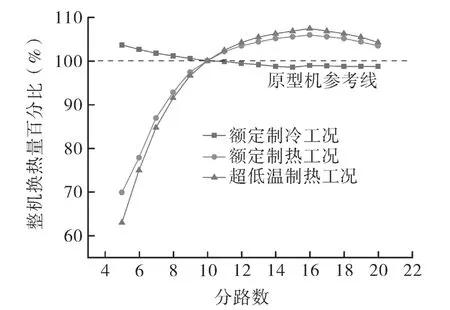
图6 各工况系统能效随分路数变化趋势Fig.6 Variation trend of system performance under various working conditions with the number of paths

在制冷工况下，随着分路数增加，整机能效呈现减小趋势，分路数为5～7 时，制冷能效相较于原型机提升最明显，约为3.6%～1.7%；在额定制热工况下整机能效呈现先增加后减小的趋势，分路数为14～16 时能效提升最明显，约为5.1%～5.9%；在超低温制热工况下整机能效也呈现先增加后减小的趋势，分路数为14～16 时能效提升最明显，约为6.2%～7.4%。将图4 与图6 对比可知，同换热量下整机能效变化趋势与同频率下换热量变化趋势相近，这也是室外换热器压降与平均传热系数之间权衡的结果。此外，可以看到，超低温制热工况整机能效随分路数变化幅度较额定制热工况更大，原因是超低温制热工况制热性能受压降影响更明显，增加分路数、减小压降能取得更好的改善效果，减小分路数造成的恶劣影响也更大。

综合2.2 节与2.3 节，对于额定制冷工况，换热器分为5～7 路时系统能力与能效表现最优；对于额定制热及超低温制热工况，换热器分为14～16 路时系统能力与能效表现最优。制冷与制热模式下优选分路数具有明显差异，常规的换热器只能在2 种模式最优流路数之间选取折中，会导致换热器性能的下降，因此本文提出了一种新的可变流路方法，通过一些阀件使得制冷与制热模式下室外换热器均运行在其优选流路，并通过试验进行对比验证。

3 可变流路设计及试验分析

3.1 可变流路设计

基于前文分析，综合考虑仿真结果及可操作性后确定最终优化方案为：制冷7 路，制热14 路。由于制冷和制热的最优分路数不同，本文提出一种设计方法，通过单向阀和电磁阀来实现制冷与制热模式下室外机流经不同分路数的目的。在制热模式时电磁阀关闭，室外换热器分14 路进行换热；在制冷模式时电磁阀打开，由于单向阀的存在，制冷剂流经7 路换热管路后，通过电磁阀进入另外7 路换热管路进行换热，此时室外换热器整体分7 路进行换热，如图7 所示。

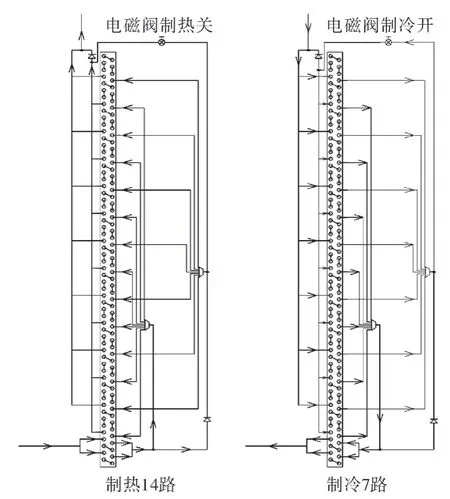
图7 可变流路样机流路Fig.7 The diagram of variable refrigerant flow paths

3.2 试验误差分析

将原型机与所制作可变流路样机放于国家认可的同一10P 焓差室内进行测试对比。试验过程中测量仪器的测试数据具有误差，故常采用不确定度来评估试验值与真实值之间的偏差［27］。直接测量物理量的偏差常采用B 类不确定度表示，B 类不确定度采用下式进行计算：

式中，RS为被测物理量的仪表分度或精度。

计算结果见表5。

表5 直接测量物理量的最大不确定度Tab.5 Maximum uncertainty of direct measurement of physical quantities

间接测量参数换热量Qa与系统性能COP的相对不确定度采用式（17）（18）计算［11］：

式中，ma为空气质量流量，kg/s；Ta，in为空气入口温度，℃；Ta，out为空气出口温度，℃；Cpa为空气定压比热容，J/（kg·K）；Wtotal为输入功率，W。

计算得到Qa及COP的最大相对不确定度分别为1.24%与1.26%。试验主要性能参数的相对不确定度均在3%以下，满足试验精度要求。

3.3 试验数据分析

通过试验测试对比了APF测试中各工况的能效及超低温制热工况的能力与能效。在测试APF时需保证各工况能力满足国标的要求，因此通过调节压缩机频率使得系统能力相当，这样对比系统能效才具有实际意义。在测试超低温制热工况时，保证压缩机运行频率相同。

试验测试结果见表6，7。在APF各测试工况下，可变流路样机能效的试验值较原型机均有提升，APF试验值较原型机可提升约为5.4%，超低温制热工况系统能力与能效分别提升了6.0%与2.8%，可变流路设计具有有效性。在制冷模式下，可变流路样机及原型机的室外机冷凝器分路数分别为7 路与10 路，由前文分析可知冷凝器本身压降较小，其倾向于更少的流路数以提高传热系数，此时采用7 路可有效改善换热器性能，从而提高系统制冷性能。在制热模式下，可变流路样机及原型机的室外机蒸发器分路数分别为10 路与14路，由前文分析可知蒸发器本身压降较大，其倾向于更多的分路数来降低压降，此时采用14 路可有效降低蒸发器压降，改善其性能。

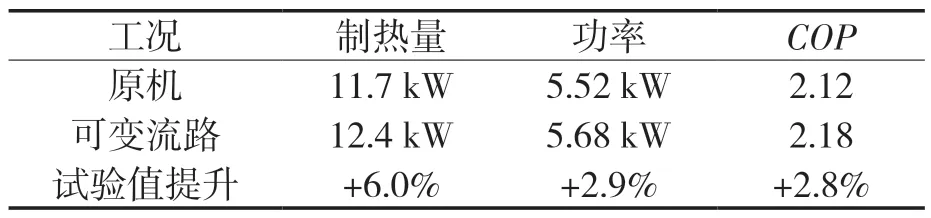
表7 超低温制热工况对比Tab.7 Comparison of ultra-low temperature heating conditions

此外，表6 也列出了原型机与可变流路样机仿真值及试验值的偏差。各工况能效试验值及仿真值偏差在8.4%以内，除最小制热外其他工况能效偏差在3.8%以内，原型机及可变流路样机的APF试验值与仿真值偏差在2.5%以内，这表明系统仿真模型具有较高准确性及可靠性。

4 结论

（1）单体换热器仿真结果表明，不能通过单体换热器仿真得到的换热量大小来评判流路优劣，对单体换热器进行仿真只能定性分析不同流路下换热量及压降的变化情况，无法确定不同流路在整机系统中的表现情况。

（2）系统仿真结果表明，与同能力下的原型机相比，额定制冷工况下流路5～7 路时整机能效表现最优，提升约为3.6%～1.7%；在额定制热工况流路14～16 路时系统能效表现最优，提升约为5.1%～5.9%；在超低温制热工况流路为14～16 路时系统能效表现最优，提升约为6.2%～7.4%。

（3）设计了制冷与制热模式下室外机运行分路数分别为7 路与14 路的可变流路方案，试验测试结果表明各APF测试工况下能效均较原型机有提升，APF提升约为5.4%，超低温制热量和能效分别提升了6.0%和2.8%。此外，各工况能效的试验值及仿真值偏差在8.4%以内，除原型机最小制热外其他工况能效偏差在3.8%以内，原型机及可变流路测试机的APF试验值与仿真值偏差在2.5%以内，这表明系统仿真模型具有较高的准确性与可靠性。