基于物理信息神经网络的激光超声波场研究

颜 鑫,应恺宁,戴鹭楠,谭钧夫,沈中华,倪辰荫*

(1.南京理工大学 电子工程与光电技术学院,南京 210094,中国;2.南京理工大学 理学院,南京 210094,中国;3.南京理工大学 计算机科学与工程学院,南京 210094,中国)

0 引 言

激光技术在检测领域[1]应用十分广泛,其中激光超声[2-4]技术是无损检测[5-8]领域的重要研究工具。激光超声与传统超声[7]相比有许多优点:激光超声不仅能够在固体中产生,同样可以在液体、气体中产生;并且依据材料的不同性质,激光声源能激发出纵波、横波和表面波等多模态波,是一种理想的声源。波场成像[9-13]方法可用于表征和研究各种材料系统中的弹性场相互作用。其中基于激光超声的波场成像方法,即使用扫描激光测振系统[11]来检测由超声激发源产生的材料表面上的运动,通过重复的激发超声,测振系统在不同的检测点能够得到一组离散的时间序列信号(离面位移-时间信号),这些随时间变化的数据显示了超声在材料内部传播的细节。基于激光超声的波场成像技术,利用可视化的超声波场图像对材料性质进行分析,并且有着激光超声无损检测高精度、非接触和无损伤的优点,因此有着重要的意义和应用背景。

近年来,随着深度学习算法的更新迭代和数据的爆炸式增长,深度学习已经在生物医学[14]、自动驾驶[15]、图像识别[16]、自然语言处理[17]等领域取得了突破性进展。传统深度学习算法的任务就是建立输入数据到输出数据直接的映射关系,即提供一个训练集,包括输入和其对应的输出,如果神经网络的输出结果是错的,它将会调整计算,并在训练集上不断重复计算,直至得到期望的结果。为了找出这种映射关系,通常需要数据对网络进行训练。当数据量过少时,模型无法得到准确的结果;而当数据量过于庞大时,又会导致模型的泛化能力过差,模型陷入过拟合。因此最终训练出来的模型好坏与数据息息相关。在许多物理模型之中,训练的数据之中往往暗含着物理定律,但是这些都没有体现在传统的深度学习算法之中。因此,为了规避数据稀疏性的影响,让神经网络也能够利用物理定律,布朗大学RAISSI等人[18-20]提出了一种基于物理信息的神经网络(physical-informed neural networks,PINN),结合了数据驱动和物理模型的优势,能在少量数据下训练出符合物理规律的模型,避免了模型过拟合并提高了其泛化能力;在此基础上,RAISSI教授证明了在构建物理系统的正向问题和反向问题上,可以使用偏微分方程作为先验信息来约束最小化过程,即PINN可以用于解决物理模型的正反问题。在正向问题中,可以得到偏微分方程的近似解;而在反向问题中,可以计算出偏微分方程所涉及的参数甚至是未知的函数。由于可在PINN中引入基于物理规律的表达式,许多学者已经将其在不同的领域进行了应用,例如流体力学[21]、生物医学[22]、材料领域[23]等。PINN在激光超声无损检测领域的应用目前仍处于起步阶段,但是激光超声信号满足波传播的物理定律,因此可以以此建立物理模型。

针对上述问题,本文作者开展了正向重建激光超声波场图像和反向推演波速的研究。首先,基于声波波动方程建立了PINN模型,并使用数值计算实验获得的激光超声信号作为输入数据,对所建模型进行了训练;其次,利用神经网络作为函数逼近器,在数值计算模型的表面波波场数据基础上,正向训练出表面波波场图像,减小了数据稀疏性对于神经网络的影响;最后,利用表面波数据进行PINN参数反演,神经网络自动推演出表面波波速,即建立的PINN模型可以用于反演偏微分方程(波动方程)里面的参数。

1 基于波动方程的PINN基本理论

1.1 PINN基本理论

传统神经网络[24-25]为一个多层的网络结构,分为“输入层”、“隐藏层”和“输出层”,如图1所示。在这3层结构中,“输入层”接收待训练的数据;“隐藏层”可以不止一层,每一层有多个神经元,其接收前一层的数据进行非线性运算,运算的结果为“输出层”的输入;最后“输出层”输出结果。其中“输入层”、“隐藏层”和“输出层”两两连接。

图1 神经网络结构Fig.1 Structure of Neural network

图1中,x1～xn为“输入层”的输入值,输入值在经过神经元后会进行非线性变化,如下式所示:

(1)

式中:σ(·)表示激活函数;j表示该层的神经元的个数;n表示输入的个数;wj表示该层第j个神经元为输入值赋予的权重;xj为第j个神经元的输入,即为上一层的输出值;b表示该隐藏层神经元带有的偏置;Zj为该层的输出值,也是下一层的输入值。

本文中基于波动方程建立PINN模型,与普通的神经网络相比,在激活函数的选择上面需要注意以下几点:首先,由于波动方程涉及到偏微分方程的运算,所以需要激活函数的2阶导数存在、且不为0,例如激活函数ReLU就不能运用;其次,例如sigmoid和tanh等存在2阶导数且不为0的激活函数都可以使用,而在实际训练模型的时候,由于检测到的振动幅度较小,使用sigmoid激活函数容易出现梯度消失的问题,因此实际使用中tanh较好,表达式如下式所示:

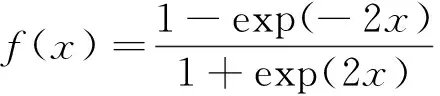
(2)

在神经网络中,“输入层”到“隐藏层”都会进行这种非线性变换,而在“隐藏层”到“输出层”中将进行线性变换,如下式所示:

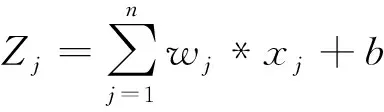
(3)

“隐藏层”到“输出层”进行运算时,如式(3)所示,只进行线性运算。经由神经网络模型计算出来的预测值,将继续作为偏微分方程的输入,计算残差。

PINN将利用控制超声波传播的线性2阶偏微分方程[26-27],如下式所示:

u″=c2Δu,(x∈Ω,t∈[0,T])

(4)

式中:u(t,x)是偏微分方程的解;t是时间;c表示波速;Ω是表示实数集;u″是离面位移u对时间t求2次导数;Δu表示对u进行拉普拉斯运算;T代表求解时间域。网络结构原理如图2所示。

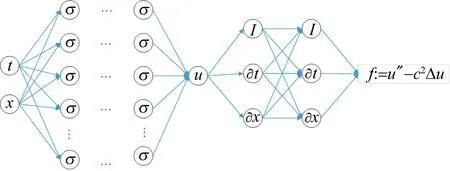
图2 PINN结构图Fig.2 Structure of PINN

图2表示PINN先建立一个神经网络的位移逼近函数u(t,x),之后建立偏微分方程的残差f,f的值越趋近于0表示神经网络的预测值越符合物理模型,表达式为:

f:=u″-c2(x)Δu

(5)

式中:“:=”表示更新参数。定义PINN的损失函数为:

L=λMu+Mf

(6)

式中:λ>0为惩罚项系数,通过改变λ,可以调整神经网络的逼近函数,从而达到帮助神经网络快速收敛的效果;Mu为神经网络预测值up和真实值u的均方根误差;Mf为偏微分方程的残差f的均方根误差,其表达式分别为:

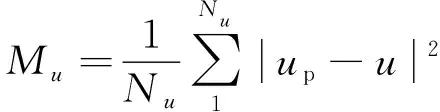
(7)

(8)

式中:Nu表示预测值的总个数;Nf表示偏微分方程采集点的个数。

1.2 优化算法

由第1.1节可知,多层神经网络在训练中需要经过多次迭代计算,每次迭代根据当前神经网络的权重和偏置计算输入数据前向运算的结果,根据建立的损失函数来计算神经网络的输出与目标输出之间的误差,此时需要反向传播计算损失相对于参数的梯度,使用梯度下降算法更新参数以减少下一次迭代的损失。

梯度下降算法更新公式为:

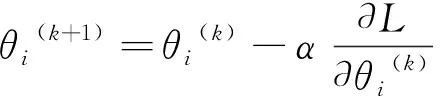
(9)

式中:θ为待更新参数;α为学习率,决定了梯度更新的步长;L为损失误差;∂为偏导数符号;上标k为迭代的次数;由于神经网络之中需要迭代更新的参数往往为多个,下标i对应不同的参数。由式(9)可以看出,如果学习率过小,损失函数的变化速度会很慢;如果学习率过大,可能会使损失函数直接越过全局最优解,陷入局部最优解。本文中采用自适应矩估计(adaptive moment estimation,Adam)优化算法[28],收敛速度比传统的梯度下降算法更快,不易陷入局部最优。

本文中均采用4层神经网络,每层有128个神经元,激活函数为tanh,优化器为Adam。

2 激光超声数值计算模型及参数设置

为利用PINN进行波场成像及参数反演,首先使用仿真软件进行数值计算以获取波场数据。在数值计算模型中,利用固体力学和固体传热两个模块[29],模拟了激光入射在铝材料上导致局部吸收能量形成热弹激光超声这一过程[30-31]。本文中通过固定超声激发点,会在材料表面产生超声信号,而通过移动扫查探测点可以测得不同位置的离面位移信号,即物体表面质点震动离开表面原位的距离,从而进行数值计算实验研究。通过设置不同的激发点位置和探测点扫查范围,得到了两组数据。

数值计算的第1组数据如图3中激发位置与扫查范围1所示。样品材料设置为铝,长度为6.0 mm,厚度为1.0 mm,其中激发点位于上表面中心处,位置设为0点。测量范围在整个上表面[-3.0 mm,3.0 mm]区域,每步扫描步长为50.0 μm,共包含121个扫描点,时间步长数据采集间隔为0.02 μs,101个总时间步长点共2.0 μs。数据以(Nx,Nt)的形式排列,大小为(121×101),其中Nx为x方向的网格点,Nt为总时间步长。B扫图像u(t,x)如图4a所示,其中横坐标表示时间,纵坐标表示探测点的位置,两条直线分别为掠面纵波、表面波。直线的斜率表示为该波的波速。可以发现:在x=0.0 mm处,由激发光辐照产生的热膨胀离面位移远远大于其它探测点的离面位移,由热膨胀引起的离面位移为纳米级,图4a中为一条黄绿色的横线(即图4a中激发点处热膨胀信号),而超声传播过程中的离面位移数量级为0.01 nm,热膨胀信号至少比超声信号引起的离面位移大两个数量级。

图3 数值计算模型(固定激发、多点探测)Fig.3 Numerical calculation setup for fixed generation and multiple point detection

图4 激光超声多模态B扫图像a—探测点包含激发点 b—探测点不包含激发点Fig.4 B-scan image of laser ultrasonic multi-modea—when detection points include the excitation point b—when detection points exclude the excitation point

数值计算的第2组数据如图3中激发位置与扫查范围2所示。样品表面宽度为6.0 mm,深度为1.0 mm,其中激发点位于上表面中心点左侧1.0 mm处。波场成像测量范围在上表面[0.0 mm,3.0 mm]区域,模拟扫描步长100.0 μm(31个扫描点),时间步长数据采集间隔为0.02 μs(101个总时间步长点共2.0 μs)。B扫图如图4b所示,与图4a的区别在于此时的探测点不包含激发点,但都有掠面纵波和表面波,其斜率代表各自的波速。其中热膨胀处的离面位移为纳米级,而由于超声传播特性而引起的离面位移也为纳米级,因此,激发点无法体现出超声传播所引起的离面位移变化。

需要指出的是,激光超声具有多模态激发的特性,针对这一特性,本文作者提出的PINN模型可以加入不同的控制方程表示不同模态的特点。为了研究方便,先从单模态超声传播着手,研究激光超声中波场成像原理。因此,本文中PINN模型只对单个波进行建模分析,由此,作者先对波场数据进行预处理操作。由图4可知,B扫图像包含掠面纵波、表面波等多个超声波模态。从时域信号幅值来看,除激发点外,表面波幅值比其它模态声波大一个数量级,所以选取表面波模态进行分析。取表面波信号最大幅值处为其到达时间,处理后的单模态数据如图5所示。横坐标均为时间,纵坐标均为探测点的位置,直线的斜率为波速。

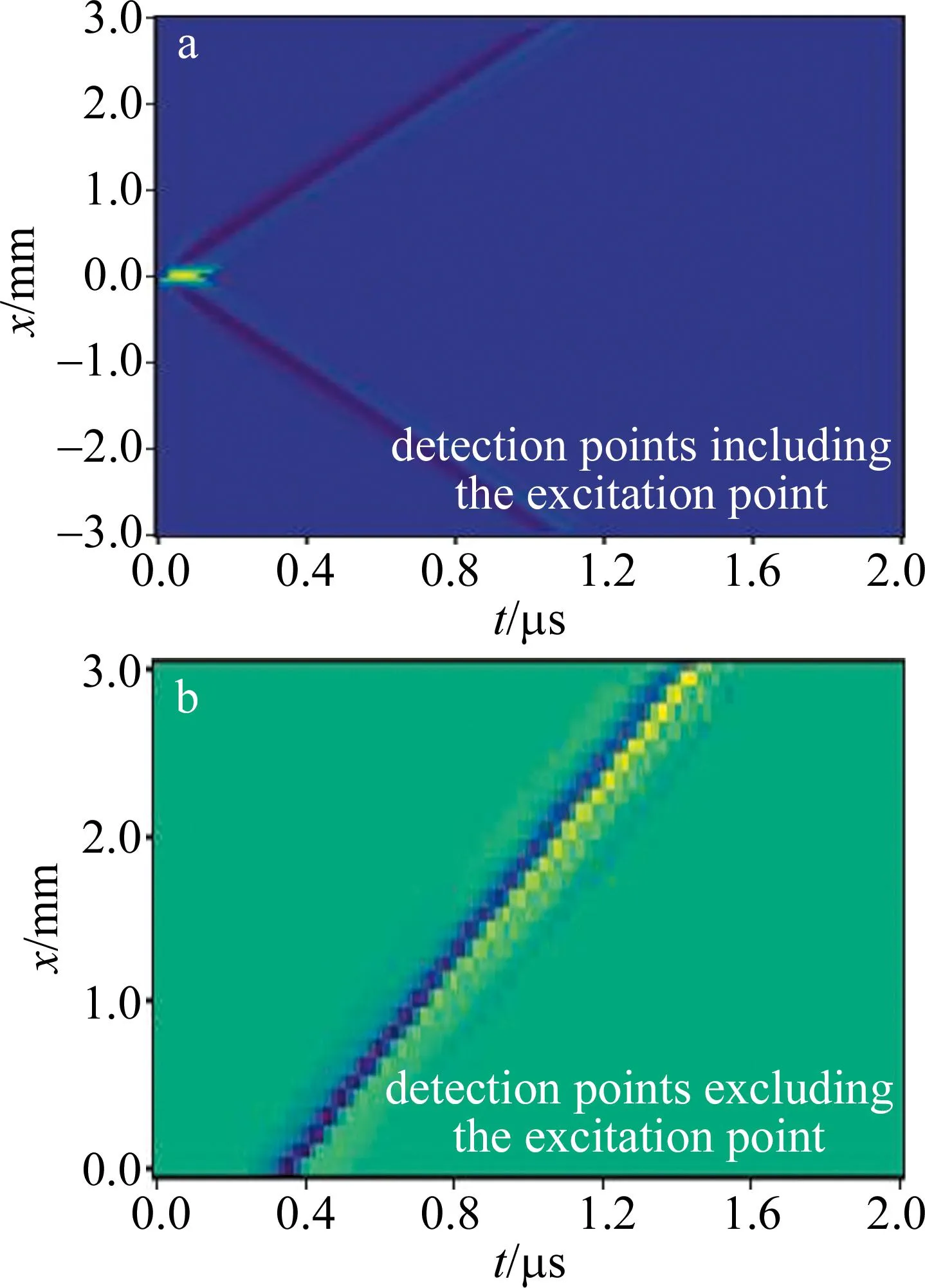
图5 激光超声单模态B扫图像Fig.5 B-scan image of laser ultrasonic single-mode

在训练PINN模型时,为验证PINN模型能用少量数据重建波场的可行性,在均匀采样、扫描距离和总时长均一定的前提下,增大扫描步长和时间步长,再将少量数据输入PINN中进行训练,最后与原始扫描步长和时间步长的波场数据进行对比。

3 结果与讨论

本节中使用数值模型中获得的2组计算数据,对上文建立的基于波动方程的PINN模型进行训练,从而正向得到激光超声单模态(表面波)波场图像的结果,进而反向推演激光超声单模态波场参数。

3.1 单模态激光超声波场的正向计算

为了利用少量的波场u(t,x)数据重建波场图像,首先进行第1组数值计算数据(数据大小为121×101,共12221个数据点)训练PINN模型。图6a为正向PINN模型重建出来的B扫图像,其中横坐标为时间,纵坐标为探测点的位置。从图6a中可明显看出,在x=0.0 mm处的离面位移远远大于其它探测点处的离面位移,这是由于数值模型中激发点的离面位移远远大于其它点,在训练模型过程中被作为了主要特征。

图6 探测点包含激发点时前向PINN训练结果Fig.6 Forward PINN training results when detection points include the excitation point

图6b中给出了PINN模型训练过程中的损失函数的变化过程。图中横坐标表示迭代次数,纵坐标表示损失函数的值。由图6b可知,训练数据包含探测点时,损失函数的值基本平稳无法下降。这是由于x=0.0 mm处的离面位移主要由激发源导致的热膨胀引起,其幅值比其它探测点处获得的离面位移高了一个数量级,因此PINN模型会将x=0.0 mm点的数据作为主要训练特征。而PINN模型是基于波动方程构建残差损失的,x=0.0 mm处的热膨胀引起的离面位移并不能在波动方程中体现,因此与损失函数矛盾且损失函数无法下降。

针对这一问题,使用扫查路径不包含激发点的第2组数值计算数据(大小为31×101,共3131个数据点,扫描步长为100.0 μm,时间步长为0.02 μs)中约10%的数据(大小为16×21,共336个数据点,扫描步长为200.0 μm,时间步长为0.1 μs)训练PINN模型。与上述情况不同,其损失函数可以收敛,下降趋势如图7所示。

图7 探测点不包含激发点时的正向PINN模型损失函数Fig.7 Loss function of forward PINN model when detection points do not contain the excitation point

图7表示第2组数据作为训练数据时,PINN模型训练过程中的损失函数的变化过程。除个别跳变点之外,PINN模型的损失函数逐渐接近零,平稳地趋近于收敛。这表明当探测点不包含激发点时,第1组数据中作为主要干扰信息的热膨胀源不存在,正向PINN模型可以利用波场数据重建波场图像。对于训练出来的PINN模型,图8表现了其重建B扫图像的结果。其中图8a表示PINN模型重建出来的B扫图像,图8b表示PINN模型预测的数据与数值计算数据的相对误差图。由图8b可知,将PINN计算的数据与数值计算数据进行对比,误差主要集中在表面波到达时刻点附近,波场数据u(t,x)的平均误差为0.0123 nm,其误差相比于原始波场数据下降了一个数量级(超声传播过程中引起的离面位移为纳米级)。图8c和图8d为随机选取了x=0.5 mm,x=1.0 mm的时间-位移波形图像。可以看出,PINN拟合的表面波与数值模拟实验的表面波数据的波形基本一致。

图8 探测点不包含激发点时前向PINN训练结果Fig.8 Forward PINN training results when detection points do not contain the excitation point

由上述可知,在训练正向PINN模型时,探测点包含激发点时,由于激发点处产生的大幅度热膨胀,导致待训练数据的内部数据规律与PINN模型内置的波动方程信息不对应。由此可知,训练PINN模型时主要特征需要符合模型中作为判据的物理信息(在本例中,是式(5)的波动方程)。本文中,当与物理规律无关的干扰源高于波场数据引起的离面位移一个数据量级乃至以上时,式(6)中的损失项Mu中激发点的数据将作为主要特征,与损失项Mf中的波动方程相矛盾,PINN模型将不收敛。

3.2 单模态激光超声参数的反向推演

在正向利用PINN模型重建波场图像之后,下面进行单模态激光超声信号参数的反向推演。对于给定的波场u(t,x),目标是识别未知参数波速c。反向PINN模型对于噪声信息有着更好的鲁棒性,因此,即使探测点包含了激发点,也可以反演出波速c。使用第1组数值计算模型的数据中约25%的数据量(大小为61×51,共3111个数据点,扫描步长为100.0 μm,时间步长为0.04 μs)进行训练反向PINN模型。图9a中给出了PINN重建出来的B扫图像,横坐标为时间,纵坐标表示探测点的位置,图中的斜线为表面波到达每个探测点时刻,在x=0.0 mm处为激发点。图9b表示PINN模型预测的波场数据与真实数据的绝对误差分布。由图9b可知,其误差主要也是集中在激发点附近和表面波到达时刻附近,这是由于训练的数据之中包含一部分噪声的干扰,波场数据u(t,x)的平均绝对误差为0.0046 nm,计算误差与原波场数据相比下降了4个数量级。图9c和图9d为随机选取x=-1.5 mm,x=2.5 mm时的时间-位移图像,波形基本一致。

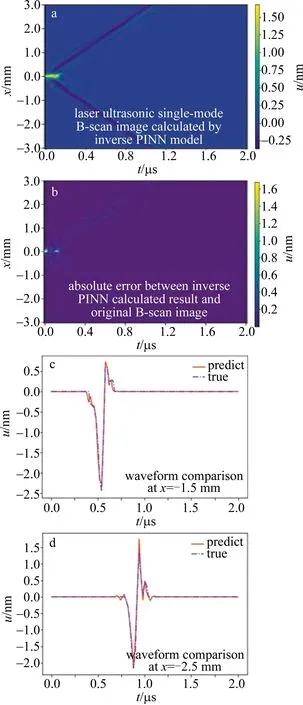
图9 探测点包含激发点时反向PINN训练结果Fig.9 Inverse PINN training results when detection points include the excitation point

表1中给出了反向推演的波速结果。从表中可知,PINN反演出来的波速与真实波速相比,误差为3.28%。

表1 真实波速和PINN反演波速(包含激发点)Table 1 True wave velocity and velocity inversed by PINN (including the excitatiion point)

由于已经证明了反向推演参数对于干扰数据有更好的鲁棒性,接下来讨论小数据训练PINN模型时波场成像质量的问题。利用给定的波场数据u(t,x),在数据中不包含激发点数据的情况下,识别未知参数波速c。本次使用了第2组数值计算模型的数据中约21%的数据量进行训练PINN模型(大小为31×21,共651个数据点,扫描步长为100.0 μm,时间步长为0.1 μs)。图10a为PINN模型重建的B扫图像;图10b表示PINN预测的波场数据与真实数据的绝对误差。平均绝对误差为0.0046 nm,相比于原波场数据,平均绝对误差下降了一个数量级。图10c和图10d为随机选取的x=1.0 mm,x=2.0 mm时的时间-位移波形图像,将PINN预测的数据与真实的数据进行对比,PINN拟合的表面波与真实数据的表面波基本一致。

图10 探测点不包含激发点时反向PINN训练结果Fig.10 Inverse PINN training results when detection points do not contain the excitation point

如表2所示,PINN反演出来表面波波速,与真实表面波波速误差为1.80%。

表2 真实波速和PINN反演波速(不含激发点)Table 2 True wave velocity and velocity inversed by PINN (excluding the excitation point)

经过两组不同的数据训练出来的PINN模型均可以反演出波速,且误差均在5.00%以内。第1组数据其探测点包含了激发点,PINN模型仍可以反演出模型;第2组数据训练出的反向PINN模型的误差比正向PINN模型的误差低了一个数量级,显示出了PINN对噪声的鲁棒性(抗干扰性)很强。这是由于反向训练PINN模型时,波速是未知参数,参与训练时以波动方程为主要特征进行训练,通过调节惩罚项系数λ调节神经网络模型,而在正向训练PINN时,由于激发点处热膨胀导致离面位移比其它探测点高了多个数量级,波动方程的残差损失无法作为主要特征,因此,在正向过程中无法重建包含探测点的波场图像。同时,由于波动方程作为主要特征学习时,神经网络能够减小其它干扰噪声的影响,所以第2组数据的反向成像质量也优于正向过程。

需要指出的是,本文中目前只利用描述激光超声传播的波动方程进行波场重建以及反演内部参数,并依此对单模态超声信号进行分析。在激光超声检测技术中,还可进一步针对激光超声多模态特性,分别对不同模态的激光超声信号建立独立的控制方程来重建不同模态激光超声信号的波场及参数反演。此外,在其它光学研究领域,这一将物理信息嵌入神经网络的方法同样适用于基于麦克斯韦方程物理信息的研究场景,如光电器件仿真领域。这些基于物理信息的神经网络模型可为激光仿真技术的研究提供其它可行思路。

4 结 论

介绍了PINN用于正向求解波动方程和反向推演参数的原理,利用神经网络的逼近理论和自动微分技术,PINN可以帮助人们避免许多传统神经网络会遇到的问题,例如:数据量过于稀少、模型的泛化性不够等;进一步证明了PINN求解波动方程时,在数据量稀疏的情况下完成对波场的正向重建,以及自动反向求解波动方程的波速;最后,将其应用到激光超声领域,实现了对于表面波波场的正向重建和反向波速推演,并将结果与数值计算模型的数据进行对比。研究结果表明:重建的波场数据精确度较高,与原波场数据的绝对误差下降了至少一个数量级;在反向的过程中,PINN模型自动推演表面波波速,无需进行人为分析,且对噪声有着抗干扰性。