平转施工桥梁转体角速度及角加速度合理取值分析

2024-04-03李前名马行川张培辉

铁道建筑 2024年2期

李前名马行川张培辉

1.中铁大桥勘测设计院集团有限公司，武汉 430074； 2.广东揭惠铁路有限责任公司，广州 510630

随着国家的经济发展及“一带一路”倡议的实施，交通互联互通的需求日益增长，我国铁路、公路网络不断完善。大批新建桥梁需跨越既有铁路、公路，当跨越的铁路、公路较宽，且交通繁忙时，预制架设（拼装）、悬臂施工等常规施工方法难以在短时间内完成。转体法施工对既有铁路、公路交通的影响最小，具有明显的经济效益与社会效益，得到了广泛应用，这也使得国内桥梁水平转体技术进入了快速发展阶段。按照铁路部门的相关要求，上跨客运铁路的桥梁一般采用转体法施工，且桥梁转体需在铁路天窗点内进行。

目前，国内尚没有专门的关于水平转体桥梁设计与施工的国家或行业标准，一些地方标准［1］或行业标准［2-5］的部分章节涉及到转体施工相关内容。现有标准中，对转体角速度的限值均在0.01 ～ 0.02 rad/min。部分标准还增加了转体悬臂端线速度的限值，在1.5 ～ 2.0 m/min。由此换算得到当转体悬臂长度在75 m以下时，不控制线速度；当转体长度大于75 m时，转体角速度须减小，以满足悬臂端线速度的要求。

一般情况下，跨线桥的交叉角度不小于60°，水平转体角度多在60°～ 90°；特殊情况下，如小角度方向有障碍物，或者曲线桥等，需要采用大角度转体。山西平城街西延段跨铁路桥曲线半径60 m，转体角度达148°，分两个天窗点进行施工，在试转6°的基础上，两个天窗点内分别转体80°、62°；上海漕宝快速路嘉闵立交跨高铁主桥顺时针转体110°；广西南宁市亭洪路延长线上跨铁路立交桥左幅转体120°、右幅转体110°。

铁路天窗点时长多为90 ～ 120 min，且一般要留出20 min作为封闭线路、接触网停电及恢复、消点等工作时间，因此实际转体有效时间在70 ～ 100 min。当转体角度为120°时，若以0.02 rad/min匀速转动需105 min，一个天窗点内无法完成。同一座桥分两次转体，加大了安全风险，增加了直接和间接成本。然而，一些工程实际采用的转体角速度超过了0.02 rad/min的限值，也并未出现任何问题。国内部分学者从转体角速度和角加速度对结构的影响方面进行了分析研究，但尚未进行系统性的归纳并提出合理建议值。

本文通过分析水平转体角速度和角加速度对桥梁结构的影响效应，以及施工、监测条件对转速和角加速度的控制因素等，并对现有研究成果进行归纳总结，结合模型试验数据，提出合理的转体角速度和角加速度限值。在保证结构安全的前提下，节约转体时间、提高施工效率，并为后续相关标准的制定提供参考。

1 转体角速度和角加速度对桥梁结构的影响

1.1 转体角速度

从力学原理上分析，匀速转动时主梁的截面拉应力本质上由离心力（F）引起，即

式中：m为转动体的质量；ω为转体角速度；r为转体力矩与转体中心的距离。

假定转动体为等截面梁，对式（1）积分可得由离心力产生的主梁悬臂根部截面应力（σ1)为

式中：ρ为梁的体积密度；l为转体梁的梁端至转动中心的纵向水平距离，即悬臂长度。

根据式（2）可对根部截面的拉应力进行粗略估算，混凝土梁ρ取2 650 kg/m3，ω应换算为国际量纲rad/s。

匀速转动时根部截面估算拉应力见表1。可知，匀速转动产生的离心力引起的截面拉应力较小，悬臂长度80 m，且转速达到2.0 rad/min时，最大应力仅为9 422 Pa。

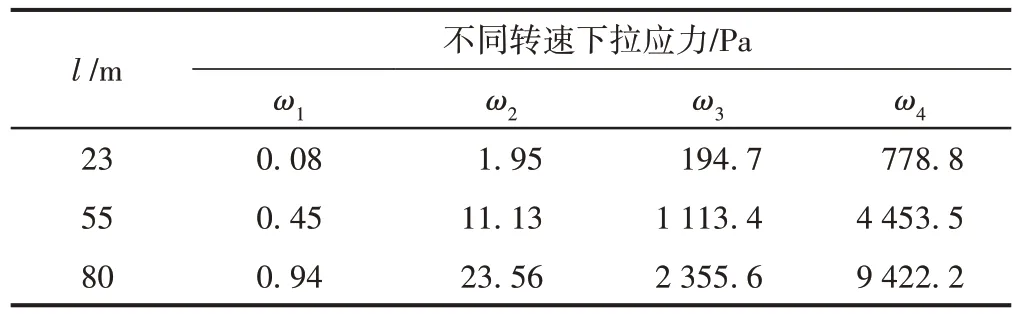
表1 匀速转动时根部截面估算拉应力

文献［6-9］通过建立有限元数值模型的方式，分析了理想状态下平转速度对结构的影响。理想状态包括以下假定：①上下转盘接触表面光滑，曲面椭圆度圆顺，材料属性不发生改变，即转动过程中不发生颠簸；②不考虑转体过程中风荷载的影响，也不考虑温度变化对球铰内材料收缩膨胀的影响，以及对主梁变形的影响；③平衡转体，只发生绕球铰中心的转动。其中，文献［6］、文献［7］分别以重庆万家沟大桥2 × 55 m预应力混凝土T构桥和郑徐客专跨符夹铁路（32 + 48 +32）m连续梁桥为例，计算了转速为0.02 ～ 2.00 rad/min时主梁结构的应力，发现主梁截面拉应力随着转速的提高而明显增大，但数值较小，当转速为2.0 rad/min时，两个主梁最大拉应力分别为7.00、0.97 kPa。

文献［6-9］的数值分析结果表明：匀速转动过程中，主梁应力分布表现为从悬臂根部到梁端逐渐减小的趋势，悬臂根部的拉应力最大，且最大应力大致与转速的平方成正比。有限元分析结果与本文式（2）是吻合的。

实际上，受转体过程中不可预见因素的影响，转体结构在平转时会伴随有整体的竖向摆动，转速增加，结构效应可能会放大。文献［10］以长安高速公路微子立交桥（72 + 120 + 72）m连续梁为例，引入振动激励荷载，采用有限元数值模拟方法分析了转体角速度、环境风速、墩高等参数对桥梁平转稳定性的影响。研究结果表明桥梁平转过程中的稳定性不仅与转速和环境风速有关，还受转体结构的自振特性影响。随着平转速度的增加，结构竖向自振周期与荷载周期越来越接近，当平转速度较快时，结构表现出明显的共振现象。

襄北编组站大桥为（200 + 294）+（226 + 200）m双独塔转体斜拉桥，单个桥塔转体质量3.2万吨，转体梁长72 m（主跨） + 52 m（边跨），转体塔高100 m（地面以上），采用中心球铰 + 周边环道支撑的多点支撑转体系统，齿轮齿条驱动［11］。为指导实桥转体施工，按1∶10比例在桥址处修建了转体试验模型。模型采用钢结构制作，试验测试了转速分别为0.02、0.03、0.04、0.06 rad/min时，分析主梁应力、承力支腿竖向应力及梁体倾角等从起始位置到转体结束的变化情况，见图1。其中，最大转角为1.54 rad（88°），支腿初始应力为4.5 MPa。

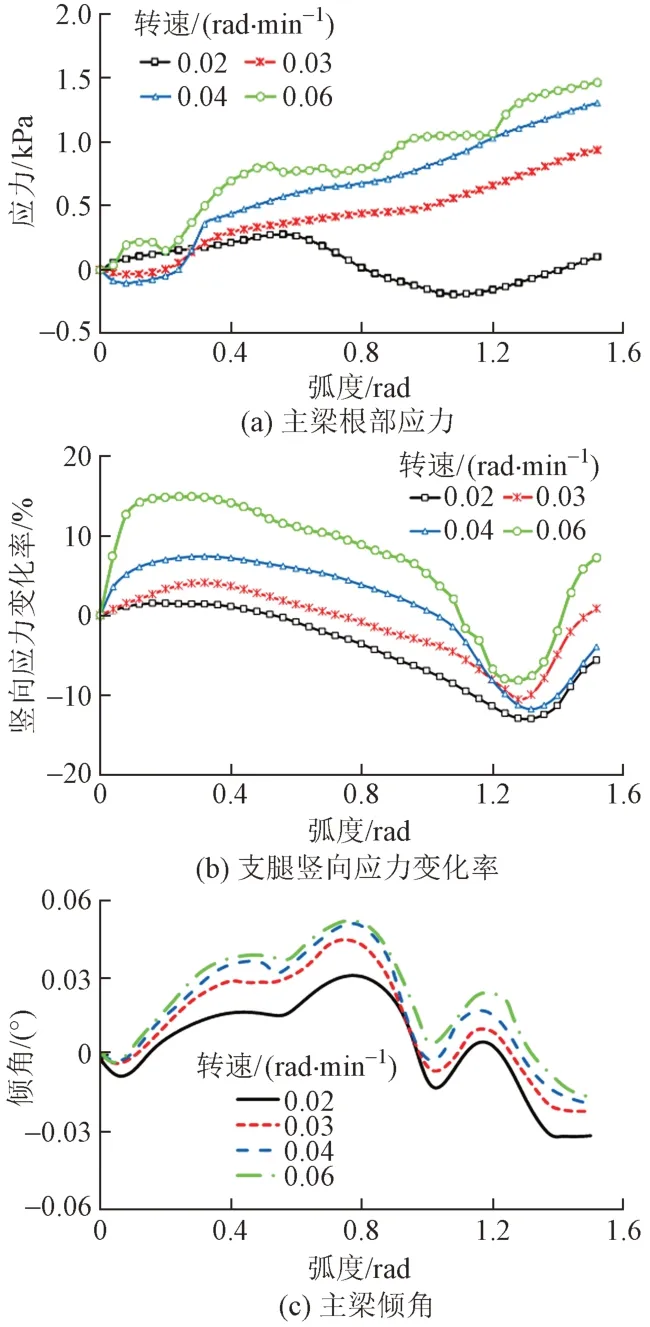
图1 试验模型结构效应与转速关系曲线

由图1可知，主梁根部应力、支腿反力、倾角均随转速的增大而增大，当转速达到0.06 rad/min时，主梁应力和支腿应力的时程曲线起伏相对较大，说明转体平稳性变差。

襄北编组站大桥实桥转体过程中，最大转速达到了0.04 rad/min，转体状态平稳，结构应力、变形等各项监测指标正常。

1.2 转体角加速度

加速转动产生的主梁截面最大拉应力与角加速度近似成正比。理论依据为牛顿第二定律，即

式中：α为转动体的角加速度。

假定主梁为等截面，利用理论力学和微积分方法推导出主梁在转动惯性力产生的弯矩作用下，任一截面的正应力（σ2）为

式中：̇为主梁单位长度的质量，也称线密度；x为计算截面至悬臂根部截面的纵向距离；y为应力计算点至截面中心的横向距离，前进一侧为负、另一侧为正；Iz为计算截面绕z轴的惯性矩。

由式（4）可知，主梁根部截面翼缘板处应力最大，且转动方向前进一侧受压，另一侧受拉。

文献［8］采用有限元模型计算了实例工程在6种角加速度（取值范围0.028 × 10-3～ 0.250 × 10-3rad/s2）作用下主梁的应力分布情况。研究发现箱梁不同部位的受力大小不同，悬臂端受力小，主梁根部受力大，且主梁截面应力呈S形分布，截面横向一侧受拉，另一侧受压。这与式（4）相吻合。

转动角速度和角速度产生的应力应满足

式中：[σ]为材料容许拉应力，C50混凝土抗拉强度设计值为1.89 MPa，可以偏于安全地不考虑预应力效应，令[σ] = 1.89 MPa。

文献［7］中实例工程计算得到的角加速度限值为1.12 × 10-2rad/s2，文献［9］中实例工程计算得到的角加速度限值为8.22 × 10-2rad/s2。文献［6-9，12］中实例工程实际采用的角加速度控制值分别为7.36 ×10-3、1.2 × 10-3、0.028 × 10-3、3 × 10-3rad/s2。按转体角速度0.02 rad/min、角加速度1.0 × 10-3rad/s2计算，从启动至达到匀速状态仅需要0.33 s。文献［8］工程实例采用的加速度对应时间为12 s，结合工程实际，该加速度取值较为合理，且由加速度产生的结构附加应力也较小。

此外，墩顶转体由扭矩产生的梁底与转动系统接触面处的局部应力，以及墩底转体由扭矩产生的墩身应力也是控制转体加速度限值的因素。

2 转体角速度对施工控制的影响

采用千斤顶张拉钢绞线牵引驱动时，转体角速度为

式中：V1为千斤顶张拉钢绞线的速度；D为上转盘的直径。

V1由千斤顶设备参数决定，其计算式［13］为

式中：Q为千斤顶泵头流量，一般为0 ～ 36 L/min；n1为牵引千斤顶的台数，一般为2台；A为千斤顶伸缸面积。

文献［13］的实例工程为（50 + 85 + 50） m预应力混凝土连续梁，转体长度2 × 40.75 m，转体质量10 000 t，千斤顶采用QDCLT2000-300型，A=0.081 996 m2，D= 8.7 m。Q取最大值36 L/min时，计算得到ω= 0.054 rad/min。说明转体角速度是受设备能力限制的，提高转体角速度需要增大设备的功率参数。

转动体到达设计位置之前千斤顶停止牵引，转动体在惯性作用下会继续转动，此时，上、下球铰间的摩阻力会迫使转动体逐渐停下来。因此，需要计算惯性制动时间，以便确定何时停止牵引，防止转体“过头”。

转动体梁端以V2的速度转动时，假定其质量均匀分布，动能（W）为

式中：V2=ωl；T动为转动牵引力，即克服球铰摩阻力所需牵引力，T动= 4μGR1/（3D），μ为动摩擦因数，G为转体质量，R1为球铰的平面投影半径；Δα为惯性制动所需要的转角位移，Δα= 1/2ωΔt，Δt为制动时间。

将式（8）简化，可得

式中：g为重力加速度。

由式（9）可以看出：依靠球铰自身摩阻力进行制动的时间与转速、悬臂长度、球铰的动摩擦因数和球铰平面投影半径相关。当l= 80 m，G= 10 000 t时，R1取1.5 m，μ可偏于保守取0.01，代入式（9）计算得到ω为0.02 rad /min时，Δt为0.06 min；若ω提高至2.0 rad/min，则Δt需要6.0 min。由此可见，制动时间占总转体时间的比例较小，不是转体角速度限值的控制因素。

需要指出的是，采用多点支撑转体、电机驱动时，由于电机可以提供反向驱动力［14］，则制动时间只与角加速度控制值相关。

3 转体角速度和角加速度的合理取值

转体桥主梁悬臂根部截面的附加应力和转体墩墩身附加应力与转体角速度、悬臂长度及墩梁截面尺寸相关，但匀速转动引起的截面应力实际数值较小，转速在1.0 rad/min以下时，其效应基本可以忽略不计。转速越大，转体过程中的振动越明显，稳定性也越差。转速在0.06 rad/min以下时，梁体振幅及转体稳定性可控。

转体角速度受设备能力的限制，一般不超过0.06 rad/min。利用上下球铰间的摩阻力进行平缓制动时，转速越大，制动时间越长，转体角速度在0.1 rad/min以下时，制动时间一般不超过20 s。

干线铁路垂直天窗点的时长一般在120 min以下，当转角为90°、转速为0.01 rad/min时，需要157 min，在一个天窗点内无法完成转体。转体角度一般不大于120°，铁路天窗点多在90 ～ 120 min，转体有效时长在70 ～ 100 min。为保证一次转体到位，则角速度下限值宜为0.021 ～ 0.030 rad/min。

相比而言，转体加速度对主梁根部及主墩底截面附加应力的影响更大，通过理论及数值分析，转体角加速度允许值数量级为10-2rad/s2。为便于监测，并将加速度对结构的影响控制在较小的范围，建议按10 ～15 s的启动、制动加速时间来确定角加速度，将角加速度控制在2.2 × 10-5～ 4.2 × 10-5rad/s2是较为合理的。此时，由转体加速度产生的附加应力基本可以忽略。

转体角加速度产生的附加弯矩及应力与转体悬臂长度的三次方成比，受滑道及球铰内部不平顺等因素的影响，实际启动后也无法保证绝对匀速转动，振动激励产生的加速度随时可能出现，且较难控制。因此，结合主梁悬臂长度选择合理的转体角速度：悬臂较小时，选择较大的转速；悬臂较大时，选择相对小的转速。

根据理论分析和工程实践，建议转体角速度最大值取0.05 rad/min，对应的悬臂长度为40 m；转体角速度最小值取0.025 rad/min，对应的悬臂长度为80 m及以上；结构效应与转体角速度及悬臂长度的平方均成比，悬臂长度在40 ～ 80 m时，转体角速度的上限值可内插取值。

据统计，跨线转体桥一次跨越2股或1股铁路的情况占70%，悬臂长度为40 ～ 70 m，由此计算得到的平转角速度在0.03 ～ 0.04 rad/min，平转120°所需时长约为52 ～ 70 min，可在一次天窗点内完成转体。

对于转体悬臂长度大于120 m的大型转体桥梁，转体角速度、加速度、振动激励等对结构的影响均明显增大。为了确保安全，建议施工阶段结构检算时考虑相关附加应力的作用，特别要控制振动引起的加速度［15］。