轨道几何状态检测异常数据实时智能识别

程朝阳 王昊 侯智雄 李颖 杨劲松 韩志 郝晋斐

中国铁道科学研究院集团有限公司 基础设施检测研究所， 北京 100081

轨道几何状态检测是及时掌握轨道几何形位、指导铁路局现场工务养护、保证铁路安全运行的重要保障。轨道检查车［1］被世界各国广泛用于检测轨道几何形位与标准值的差异，包括高低、轨向、曲率、轨距、水平、三角坑等轨道几何参数。

雨雪、大雾、草害、电子干扰等外界因素，以及数据远距离传输、设备标定误差、惯性组件自身漂移等内部因素，使得轨道几何检测系统产生异常检测数据。异常数据会产生无效的单点大值超限，同时影响200 m区段的轨道质量指数统计［2］。因此，须要进行异常检测数据识别，剔除无效单点大值超限，提高现场检测效率，减少异常数据对轨道质量指数的影响。

轨道几何状态检测数据为时序数据。关于时序数据的异常识别，相关学者已开展大量研究，主要内容集中于信号的特征构造和选用以及信号分类模型的设计。文献［3］通过小波包分形理论对传感器的输出信号进行故障特征提取，再利用支持向量机进行信号分类。文献［4］提出了一种轻量级卷积神经网络构建方法，将深度学习算法与迁移学习方法相结合，解决了领域间分布差异的问题。文献［5］提出了一种面向无标签数据的无监督、参数自适应化的故障诊断算法（Sm-DLLOF-AFCM），可以对没有任何先验信息的样本集自适应地完成故障诊断。文献［6］充分利用深度学习的深层次自动挖掘信号特征信息的能力，结合高效分类器，在区分度高的特征下实现信号的自动化特征提取和高精确度检测。文献［7］直接利用带通滤波后的时域心音信号进行心音分类，使用滑动窗将信号分割成一定长度的信号子模块，利用一维卷积神经网络进行分类。

轨道几何状态检测异常数据样本较少，构建标注数据集需要耗费大量时间精力，且神经网络分类器的设计训练及实际性能受参数影响较大，难以部署在目前算力较低的工控机上。因此，本文基于文献［8］的特征提取方法，提出一种能够进行多维特征提取的支持向量机智能分类方法。该方法模型训练时无需进行样本标注，训练集均为正常样本数据。通过对算法进行性能优化，降低算法对硬件性能的依赖，同时对算法完成结构性封装，形成模块化算法库，使之易于部署。最后，基于激光摄像组件的现场实测数据，对该智能分类方法进行验证。

1 异常数据实时智能识别算法

轨道几何状态检测异常数据实时智能识别算法分为训练阶段和在线检测阶段，流程见图1。

图1 异常数据实时智能识别算法流程

训练阶段：收集轨道几何检测系统各传感器正常状态下的时序数据，组成训练集，然后对训练集进行数据预处理操作，提取趋势项［9］；对消除趋势项后的训练集进行高维特征提取，用于训练单分类支持向量机分类器，构建异常检测模型。

在线检测阶段：对轨道几何检测系统各传感器时序数据进行数据预处理及特征提取，基于训练阶段构建的异常检测模型进行时序数据分类，将时序数据分为正常、异常两类，完成检测数据智能识别。

1.1 数据预处理

数据预处理阶段的任务是完成趋势项提取，常见的方法包括移动平均法、高通滤波法等。本文采用Hodrick-Prescott（HP）过滤器［10］，将时序序列分为趋势和周期性分量，完成趋势项提取，如图2所示。传感器原始数据采用HP过滤器消除趋势项后，可以去除基线移动，在特征提取中减小基线幅值对数据时域、频域、能量域等特征的影响，提高智能识别的准确性。

图2 数据趋势项提取

1.2 特征提取

轨道几何状态检测数据为一维时序数据，在进行训练单分类器模型时，须进行多维特征提取。为了提高模型的鲁棒性，提取了空间域、归一化振幅、频域、频谱比值、能量域、高阶统计六个大域特征，共计20个小域特征，见图3。

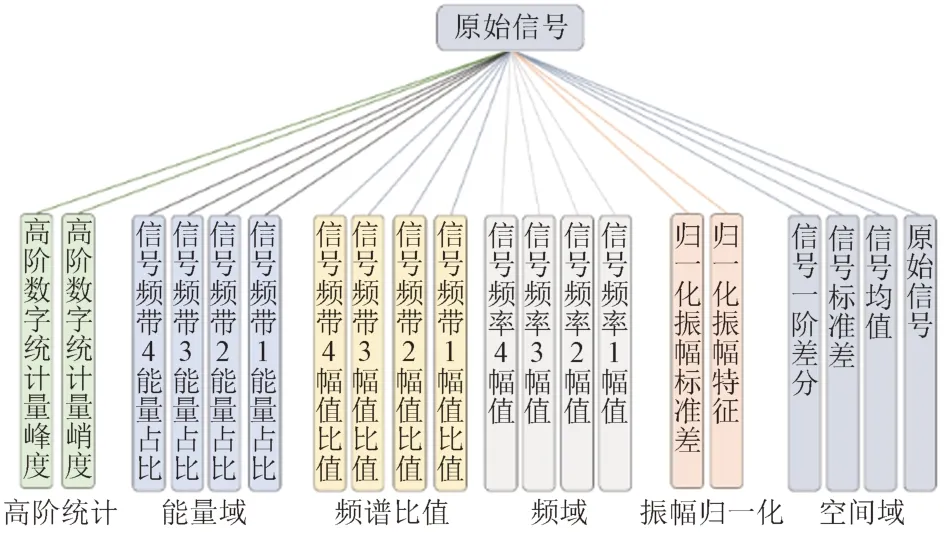
图3 数据特征

轨道几何状态数据的空间采样距离为0.25 m，以20个点即空间长度为5 m的特征队列对一维传感器数据进行步长为1的滑窗截取，然后对滑窗内的数据进行特征提取。

1.2.1 空间域特征

计算特征队列滑动窗口内的绝对值、一阶差分、二阶差分作为空间域特征，见图4。

图4 空间域特征

1.2.2 归一化振幅特征

传感器信号的异常与幅值有较强的相关性，从一维信号中提取幅值特征是合理的。同时，为了提高幅值特征的泛化性，消除传感器之间的系统差异，归一化振幅特征中不考虑绝对振幅，仅提取状态间振幅的相对比值，见图5。

图5 归一化振幅特征

采用传感器幅值之间的比值（Adiv），同时考虑幅值比值序列的一阶差分（Adivfd），构成归一化振幅特征。表达式为

式中：Ap为传感器幅值，p表示传感器空间采样幅值的索引；Amax为传感器幅值最大值，一般采用统计学意义上的最大值。

1.2.3 频域及频谱比值特征

传感器的信号异常与信号频率以及不同频段的信号分布相关。为减小直接分割数据等价近矩形窗产生的影响，减小频谱泄露，将原数据通过汉明窗，并对分帧加窗后的时域离散信号进行Welch法［11］自功率谱估计，得到自功率谱［P(f)］，见图6。

图6 频域及频谱比值特征

选取P(f)的中心频率作为第一频率特征f1，平均频率作为第二频率特征f2，频率均方根作为第三频率特征f3，频率方差作为第四频率特征f4，表达式分别为

1.2.4 能量域特征

能量域特征是滑窗内数据的带通滤波后的信号与原信号的能量比值。令初始值为0，增量带宽1 Hz，考虑4个频带，分别为（0，1］、（1，2］、（2，3］、（3，4］ Hz。依据采样定理，传感器的空间频率不会高于4 Hz，因此采用五阶巴特沃斯滤波器（filter）设计4个带通滤波器，第k个滤波器的输出是yk，表达式为

式中：bk、ak为巴特沃斯滤波器的系数向量；x为滑窗内原信号。

1.2.5 高阶统计特征

在概率论和统计学中，偏度是对实值随机数概率分布不对称性的度量，是三阶统计量；峰度是对实值随机数概率分布尾度的度量，为四阶统计量。选用偏度（K3）和峰度（K4）作为传感器数据的高阶统计特征，表达式分别为

式中：X为滑窗内空间采样数据；μ为滑窗内空间采样数据的均值；σ为滑窗内空间采样数据的标准差。

特征提取是异常识别模型的输入，所构成的数据集决定了分类模型的训练结果。本文将空间域特征、归一化振幅特征、频域及频谱比值特征、能量域特征、高阶统计特征作为识别模型的输入。高维特征在幅值范围上存在较大差距，容易影响后期模型训练，因此，将各个维度的数值均归一化到0 ～ 1。将归一化后的数据输入智能识别模型，训练拟合智能识别模型。

1.3 构建智能识别模型

传感器异常识别问题可以抽象为单分类问题。单分类问题的目的并不是将不同类别的数据区分开来，而是对某个类别的数据形成一个描述。可以理解为样本空间中的一个区域，当维度较高时为超球面。某个样本落在超球体外，则认为该样本不属于这个类别。单分类方法常用于类别极度不平衡的分类任务中，符合轨道几何检测系统异常样本较少的特性。

首先构建目标函数。假设有m个样本点，分别为x1，x2，…，xm，假设样本点分布在一个球心为A，半径为R的超球体中，那么样本xi满足

引入松弛变量（ξ），ξi≥0，允许部分样本不在这个球中，那么

目标是最小球的半径和松弛变量的值，因此目标函数（g）的表达式为

式中：C为惩罚参数。

使用拉格朗日乘数法，可将原问题表述为L(R，A，ξ，α，γ)，αi、γi为拉格朗日乘子，将αi看作xi的权重，αi≥0，γi≥0。

对参数R、A、ξ求偏导，得

化简可得

则将原问题中求L(R，A，ξ，α，γ)的最小值转化为求其对偶问题θ(αi，γi)的最大值，即

使用SMO（Sequential Minmal Optimization）算法求解上述凸优化问题，同时依据可以求取超球体的中心，R为球心和支持向量积之间的距离，zTz为样本点距超球体球心的距离。由此可得，样本是否为异常点的判别函数表达式为

单分类支持向量机的实质是通过正常数据集训练出一个超球体模型，预测的数据位于超球体中即为正常数据，否则为异常数据。单分类支持向量机是一个无监督算法，训练集数据仅需正常数据，规避了异常样本数据样本数量少的问题。

2 试验验证

以某地铁实际检测数据为例，基于左单边位移、右单边位移数据，对智能识别模型进行在线检测。单边位移异常识别效果见图7。进行数值试验时，以传感器单点异常值检测为例，基于传感器工作状态具有时间持续性的特点，对传感器区段异常采用单点异常值统计的方式进行检测。

图7 单边位移异常识别效果

根据试验结果可知，本文提出的轨道几何状态检测异常数据实时智能识别算法的识别效果较为理想，准确性较高，鲁棒性高。结合轨道几何实际工况的判别条件，可基于该算法实现轨道几何检测系统的传感器异常识别。

3 结论

轨道几何状态检测异常数据实时智能识别是检测系统智能化的前提，同时也是应对大交路（长时间）检测、无人等特殊情况在线检测以及实现自动化防错漏的重要手段。本文提出的异常数据智能识别算法准确率较高，可满足实际运用需求，提高现场检测人员的工作效率。该异常数据智能识别算法采用了轻量化设计，可快速部署，对硬件资源依赖性较低，可满足轨道几何检测系统传感器异常数据实时检测要求。