基于最优控制理论的国产光抽运小铯钟频率控制算法*

宋会杰 董绍武3)† 王翔 姜萌 章宇 郭栋 张继海

1) (中国科学院国家授时中心,时间频率基准实验室,西安 710600)

2) (时间基准及应用重点实验室(中国科学院),西安 710600)

3) (中国科学院大学天文与空间科学学院,北京 100049)

4) (西安工程大学电子信息学院,西安 710048)

5) (西安科技大学机械工程学院,西安 710054)

原子钟频率控制是时间保持工作中的关键技术.当前守时工作中的频率控制主要针对国外微波钟采用开环控制算法,但由于国产光抽运小铯钟(下称国产钟)的工作原理和性能不同于国外同类型原子钟,因此该算法不能很好适应国产钟.为了提升我国标准时间的自主性和安全性,本文基于国产钟的噪声特性,在最优控制理论的框架下研究了线性二次高斯控制算法,该算法属于闭环控制算法,从同步时间、频率控制准确度和频率控制稳定度方面研究国产钟性能,最后分析了不同控制间隔对国产钟性能的影响.结果表明随着二次损失函数中约束矩阵 WR 的增大,同步时间延长,控制准确度降低,控制短期稳定度提高.WR 相同情况下,随着控制间隔的增大,同步时间延长,控制准确度降低,控制短期稳定度提高,对于 WR=1 时,控制间隔为1 h的同步时间为5 小时,控制准确度为1.83 ns,1 h 的Allan 偏差为1.81×10–13;控制间隔为8 h 的同步时间为28 h,控制准确度为4.48 ns,1 h 的Allan 偏差为1.48×10–13.控制国产光抽运小铯钟的中长期稳定度都得到提高.

1 引言

稳定的系统时间在全球卫星导航系统(GNSS)、智能电网、电信、金融和科学实验等多个应用中具有重要意义[1–3].一个国家的法定时间通常是由实验室生成的协调世界时(UTC)的实时本地物理实现,物理实现是将本地原子钟信号控制到UTC.此外,世界各地守时实验室都将本地时间尺度控制到协调世界时(UTC)[4–6].频率控制可以利用精确的时间传递方法进行远程时钟的同步,比如基于卫星双向时间传递、全球定位系统的时间传递和基于光纤时间传递[7].

原子钟的输出频率用于产生时间标准,但是原子钟输出频率的准确度和稳定度通常不能满足时间标准的性能,需要对原子钟频率进行控制.时间保持工作中,频率控制也称为频率驾驭、频率修正等,通过将单台原子钟的频率控制到时间尺度实现守时.时间尺度是根据原子时算法计算的多台原子钟测量数据的加权平均,时间尺度的产生过程包括数据异常检测、钟差预报、权重计算,同时还要考虑时间尺度的稳健性.文献[8–10]研究了原子钟数据异常的不同检测方法.文献[11–13]研究了原子钟钟差数据的预报算法和权重算法.文献[14,15]研究了原子钟噪声变化时改进的Kalman 滤波时间尺度算法.时间尺度应用中,为给时间尺度提供物理上可实现的输出,原子钟需要控制到时间尺度.因此原子钟的频率控制是时间保持工作中非常重要的一项研究工作.频率控制算法是影响产生实时时间尺度稳定性和准确性的重要因素.

当前,频率控制研究的原子钟类型主要是微波钟,比如铯原子钟5071A、氢原子钟VCH1003M等国外原子钟,频率控制算法为基于信号的开环控制算法,即经典控制算法.比如UTC 生成中使用的控制算法[16,17].经典控制算法通过原子钟与时间尺度的相位偏差估计控制量,通常用于补偿频率偏差,必要时还用于补偿原子钟的确定性频率漂移.目前国内原子钟的研制和研究也取得了重大进展[18–20],国产钟已用于时间保持工作,但由于国产钟的工作原理、材料、制造工艺与国外原子钟不同,导致噪声特性存在一定差异,经典的控制算法不能很好适应国产钟.本文研究的国产光抽运小铯钟工艺较美国磁选态小铯钟显著简化,其优点是原子利用率高,理论性能远高于磁选态小铯钟.然而,光抽运小铯钟因引入了激光而受到光频移影响,长期频率稳定度还有待提升.目前,探索抑制和评估光频移的新方法是光抽运小铯钟技术的重要研究方向.在这种情况下,本文提出了一种可有效提升光抽运小铯钟中长期频率稳定度的方法,并进行实验验证.

基于国产光抽运小铯钟(下称国产钟)的性能特点,研究基于国产钟的控制算法,解决我国标准时间自主产生和时间基准保持的核心技术是当前面临的迫切问题.文中结合国产钟的噪声特性,建立控制模型,采用平滑控制尽量降低对国产钟短期稳定度的影响.线性二次高斯(LQG)控制是最优控制理论框架下的一种算法,可用于原子钟的平滑控制.任何控制系统都需要处理一定数量的不确定性,包括测量噪声、过程模型误差等.线性二次高斯控制(LQG)算法用于设计不确定物理过程的最优控制系统.该算法的一个重要特点是: 只要系统参数具有可观测性和可控性,就能保证控制系统的稳定性.由于原子钟数据包括测量噪声和原子钟模型噪声,需要同时考虑最优估计和最优控制.在这种情况下,LQG 算法可将最优控制问题和最优估计问题分开来处理,根据控制理论中的分离定理,可以在设计控制器时直接利用系统状态变量.而在研究原子钟状态变量的最优估计时,则可假定控制量是已知的确定性函数.最后将控制量中原子钟的状态变量用其估计值代替,就得到随机线性系统的最优控制.LQG 控制算法结合了卡尔曼滤波来估计时间和频率误差,这些误差被用作计算驾驭量.LQG 控制是Kalman 滤波器(即线性二次估计器)和线性二次调节器(LQR)的组合.Kalman 滤波可以从时间尺度和国产钟的噪声参数的先验信息中求得最优状态估计.这些噪声参数信息可以从频率稳定度图中提取.与Kalman 滤波相反,LQR不使用关于信号统计特性的信息,在LQR 中,二次损失函数使得相位和频率平方误差和控制量的和最小.LQR 通过最小化二次损失函数来计算控制量.二次损失函数中,约束矩阵影响控制性能.本文研究线性二次高斯算法控制国产钟,根据不同的约束矩阵和控制间隔,分析了控制国产钟的同步时间,控制准确度和控制稳定度,为实现国产化守时提供了理论基础和技术支撑.

本文结构如下: 第2 节在控制理论下建立国产钟的控制模型,第3 节控制测试部分,结合国产钟的实测数据,验证控制性能,第4 节给出结论.

2 国产钟的频率控制建模

原子钟的频率控制过程,需要描述系统的输入、状态和输出之间的关系.这些关系通常以微分方程的形式给出.原子钟频率控制是指在给定输出的情况下计算输入量,使系统的状态满足一定的要求.首先最基本要求是控制信号与参考信号同步,其次还要考虑驾控制信号的其他性能,主要包括准确度和稳定度性能.下面建立国产钟的状态模型:

2.1 国产钟的状态模型

对于自由运行国产钟的两状态模型可由下式给出[21,22]:

状 态变量x1(t),x2(t)分别表示相位 偏差和 频率偏差.随机过程w1(t)和w2(t) 是均值为零,自相关函数为独立高斯白噪声,k=1,2和δ(t) 表示Dirac delta 函数.根据原子钟的噪声特点,随机过程w1(t)和w2(t) 可表示不同类型的噪声过程,通常情况下w1(t) 表示调频白噪声,w2(t) 表示调频随机游走噪声.但是当原子钟也表现调频闪变噪声情况下,w1(t) 需要同时考虑调频白噪声和调频闪变噪声.

对自由运行国产钟的模型进行离散化,假设采样间隔为τ0,x[k] 表示kτ0时刻原子钟的状体向量.(1)式对应的原子钟的离散状态模型为

分量w1[k]和w2[k] 仍然是零均值高斯随机过程,当噪声过程为调频白噪声和调频随机游走噪声时,协方差矩阵表示为

当噪声过程为调频白噪声、调频闪变噪声和调频随机游走噪声时,协方差矩阵表示为

(5)式和(6)式中,h0,h-1和h-2分别表示调频白噪声幂律谱系数,调频闪变噪声幂律谱系数和调频随机游走噪声幂律谱系数,可以通过Allan 方差估计.τ0表示相邻k时刻和k+1 时刻的时间间隔.

2.2 两个自由运行原子钟的钟差模型

假设两台自由运行的原子钟,钟a 和钟b,相互独立.钟a 为参考钟,钟b 为控制原子钟.钟a 和钟b 的离散状态变量分别为xa[k]和xb[k] .假 设z[k] 是离散时间输出,也就是两台时钟之间测量的相位差:

其中e[k] 是一个随机过程,表示测量噪声,假定是均值为零,方差为的白噪声.

控制原子钟与参考原子钟的状态向量差表示为

对应的离散状态模型为

这里wz[k] 是高斯白噪声,具有零均值和协方差阵为

其中Σa和Σb是影响钟a 和钟b 的噪声协方差矩阵,由(5)式或(6)式给出.

2.3 国产钟控制系统方程及控制算法

线性二次高斯理论下,国产钟控制系统的状态方程能够表示为状态向量和控制向量的线性函数:

测量方程表示为

其中,xz,u[k] 向量中的第1 个分量表示控制国产钟与参考原子钟的相位偏差,第2 个分量表示控制国产钟与参考原子钟的频率偏差.控制量的转移矩阵为

Kalman 滤波状态估计通过下式计算:

其中Kg[k] 是Kalman 增益阵,通过极小化均方误差阵得到.均方误差阵由下式给出:

Kalman 增益计算可表示为

P-[k]R[k]

其中 表示预测误差协方差阵,表示测量协方差阵.

线性状态方程(15)是包含高阶项的状态建模方程的近似.为了给出线性近似的有效性,控制量是通过极小化二次损失函数

得到.(22)式中,求和的第1 部分是对控制国产钟状态向量的约束,第2 部分是对控制量的约束.矩阵WQ和WR是相应的约束矩阵,影响控制的强度.对于给定的损失函数,控制量通过下式给出:

基于(23)式计算的控制量在(22)式条件下是最优的,并且当 (WQΦτ0) 是可观测的,对 (Φτ0Γk) 是可控的,Kalman 滤波系统是稳定的.

3 测试结果及分析

研究目标是基于国产钟实现纸面时间尺度,然而,为了降低对控制结果影响因素的数量,控制算法将国产钟控制到参考原子钟.下文首先根据稳定度指标(Allan 偏差)分析国产钟稳定度情况和噪声特性,并与国外铯原子钟5071A(简称5071A)进行比较.然后基于线性二次高斯控制算法研究国产钟性能,最后研究不同控制间隔对国产钟性能的影响.

3.1 国产钟的噪声分析

根据Allan 偏差分析国产钟的噪声特性,首先利用氢原子钟组建立参考时间尺度,然后利用建立的时间尺度测量国产钟、5071A 和单台氢原子钟的稳定度,最后比较分析国产钟与5071A 的噪声情况.分析周期内,氢原子钟的稳定度高于国产钟和5071A.由多台氢原子钟建立的时间尺度的稳定度能够比单台氢原子钟的稳定度提升倍,也就是时间尺度的Allan 偏差是单台氢原子钟的N表示氢原子钟的数量[23].选取国家授时中心时间频率基准实验室的氢原子钟,编号为VCH067,VCH112,H336,VCH116,H297,H340,VCH119,H339,H341,VCH085,VCH104,随机选取数据时间 段2023 年2 月3 日0时至2023 年8 月25 日1 时,MJD 为59978—60181.04,数据采样间隔为1 h.每台氢原子钟扣除一个常数速率,通过取平均权算法计算时间尺度.选取国外铯原子钟5071A,编号为Cs3102,Cs2962,Cs3437,国产光抽运小铯钟,编号为Cs3050,Cs2025.数据时间段与上述对应,采样间隔为1 h.铯原子钟同样扣除一个常数速率,然后参考到氢原子钟组产生的时间尺度,得到铯原子与时间尺度的相位差.

计算铯原子钟相对于时间尺度的Allan 偏差,如图1 所示,图中还包括由氢原子钟,编号为H117,相对于时间尺度的Allan 偏差.结果显示,国产钟1 d 内的稳定度与5071A 相当,主要表现为调频白噪声.取样间隔大于1 d,国产钟的稳定度相比于5071A 的稳定度降低.5071A 的噪声主要表现为调频白噪声和调频随机游走噪声,国产钟的噪声主要表现为调频白噪声、调频闪变噪声和调频随机游走噪声.因此国产钟状态模型中的噪声协方差矩阵需根据(6)式计算.图1 显示,相应取样间隔内氢原子钟H117 的稳定度优于铯钟的稳定度,并且氢原子钟长期表现出明显的漂移.

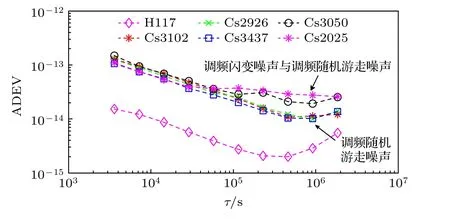
图1 铯原子钟与氢原子钟的Allan 偏差曲线Fig.1.Allan deviation curves of cesium atomic clock and hydrogen atomic clock.

3.2 线性二次高斯控制应用于国产钟的控制

线性二次高斯控制应用于国产钟的频率控制,控制模型考虑了国产钟的噪声类型,将国产钟的相位和频率控制到参考钟.图2 表示国产钟的控制结构图,系统的状态是控制国产钟的相位和频率,控制量u(t) 输入到相位微调仪,相位微调仪通过输入的控制量连续的改正国产钟的相位.自由运行的国产钟与参考氢原子钟的相位偏差测量值为z(t),控制国产钟与参考氢原子钟的相位偏差测量值为zu(t),通过控制算法极小化zu(t) .

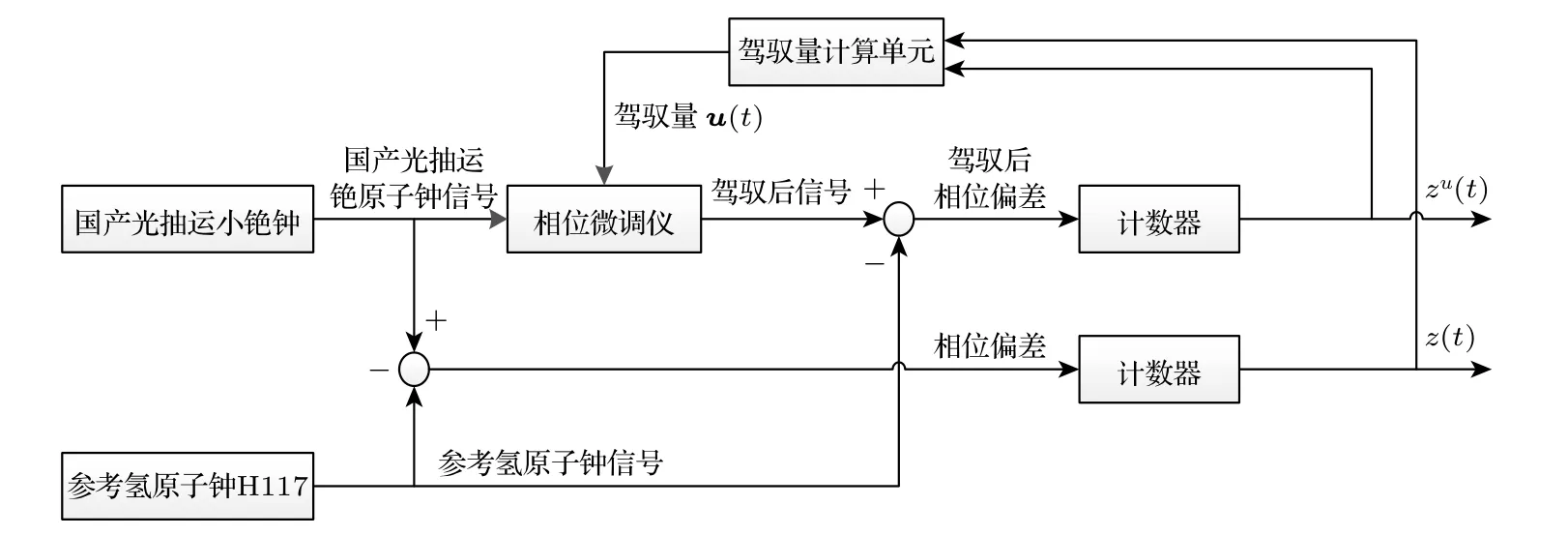
图2 国产钟的控制结构图Fig.2.Control structure diagram of domestic clock.

国产钟的实际测量钟差数据用于控制研究,测量国产钟Cs3050 与H117 的相位偏差.线性二次高斯控制方法控制国产钟到氢原子钟H117.建立国产钟控制系统的状态方程和测量方程,如(15)式和(16)式所示.状态方程中的向量包含控制的相位偏差状态和频率偏差状态,如(17)式所示.状态方程中的噪声协方差矩阵中的幂律谱系数基于Allan 方差计算.调频白噪声、调频闪变噪声和调频随机游走噪声的Allan 方差与相应的幂律谱系数的关系为

其中τ表示Allan 方差对应的平滑时间.

基于线性二次高斯控制方法控制国产钟,通过控制时钟的同步时间,控制准确度(时间偏差)和控制稳定度(Allan 偏差)的性能指标进行评估.Allan 偏差是原子钟稳定性的最常见定义,并且,基于Allan 方差可以比较不同情况下的控制结果.根据约束矩阵WQ和WR的选择,研究下面4 种情况的控制性能.

对于情况1—情况4,约束矩阵WQ不变,WR降低,算法中数据测量间隔为1 h,控制间隔也为1 h.国产钟的同步时间,控制准确度和稳定度如图3所示.

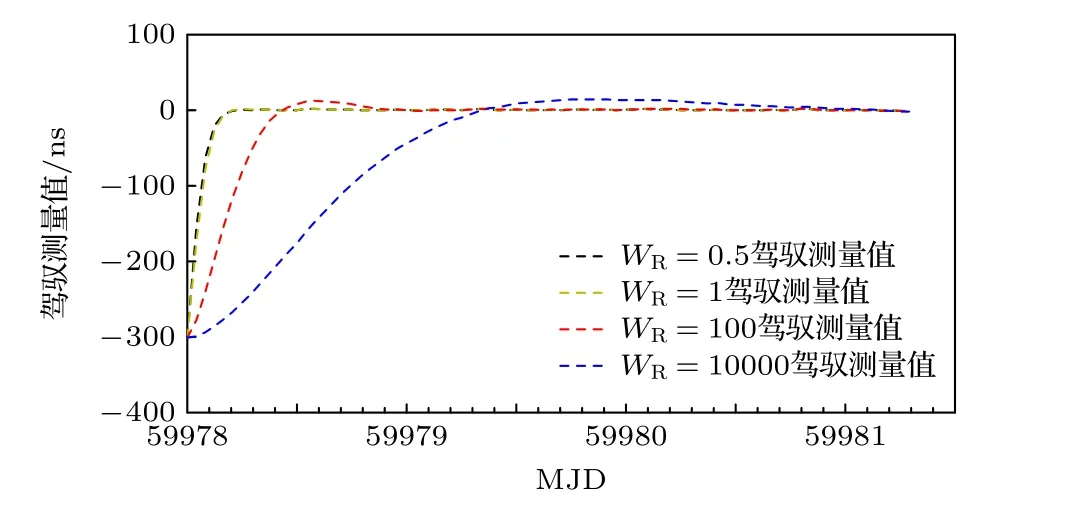
图3 不同 WR 值的控制同步时间比较Fig.3.Comparison of control synchronization time with different WR values.

图3 表示基于上述4 种情况,控制国产钟相对于参考H117 的时间偏差测量值.约束矩阵WR=104时,控制测量值需要较长时间达到0 值附近,WR=1/2 时,控制测量值需要较短的时间达到0 值附近.随着WR的降低,控制测量值到达0 值附近的时间越短.控制测量值到达0 值附近表示控制国产钟与参考原子钟同步.图4 表示控制国产钟与参考H117 同步后的时间偏差测量值.为了做图清晰,WR=1 的控制测量值加入5 ns 的常数值,WR=102的控制测量值加入10 ns 的常数值,WR=104的控制测量值加入18 ns 的常数值.从图4 可以得出,随着WR的增大,控制测量值波动变大,WR=104时控制 测量值 波动最大,WR=1/2 时控制 测量值波动最小.计算控制测量值的3 倍标准差(3σ)评估控制国产钟的准确度,在正态分布中,大约99.73%的数据位于平均值加减3 倍标准差的范围内.计算结果如表1所示,WR=104时的 3σ为6.26ns,WR=1/2 时的 3σ为1.76 ns.

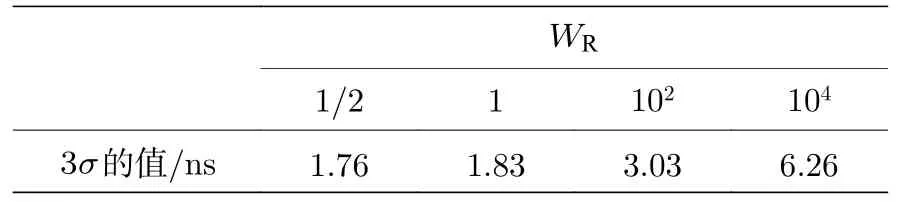
表1 同步后不同 WR 值的3 倍标准差(3σ)Table 1.Three times standard deviation of different WR values after synchronization.

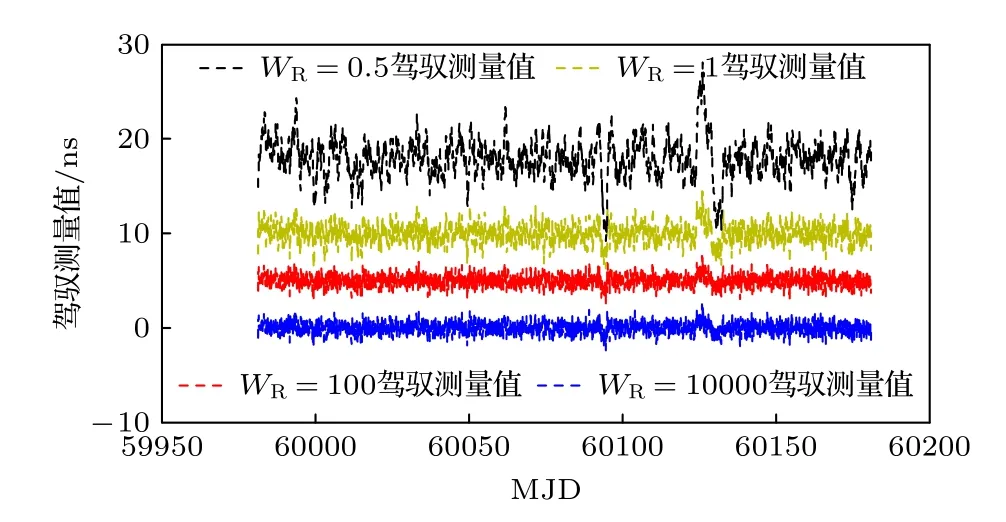
图4 同步后不同 WR 值的控制测量值Fig.4.Control measurements of different WR values after synchronization.

图5 表示基于不同WR值的控制国产钟的稳定度,稳定度的计算参考为时间尺度.图中还表示了自由运行国产钟Cs3050 的稳定度和参考氢原子钟H117 的稳定度.WR=1/2 时和WR=1 时,控制国产钟的短期稳定度(取样间隔为1 h 和2 h)略差于自由运行国产钟的稳定度.取样间隔大于2 h,控制国产钟的稳定度优于自由运行国产钟的稳定度,并且长期稳定度与参考氢原子钟H117 相符.对于WR=102,控制国产钟取 样间隔为1 h和2 h 的稳定度与自由运行小铯钟的稳定度相当,取样间隔为4 h 的稳定度略差于自由运行国产钟,取样时间大于4 h 的稳定度优于自由运行国产钟的稳定度.并且4 h 后的稳定度差于WR=1/2 时和WR=1 时的情况,最后与参考氢原子钟H117的稳定度相符.对于WR=104时,取样间隔为1—32 h 控制国产钟的稳定度与自由运行国产钟的稳定度相当;大于32 h,稳定度优于自由运行国产钟的稳定度,最终接近参考氢原子钟H117 的稳定度.

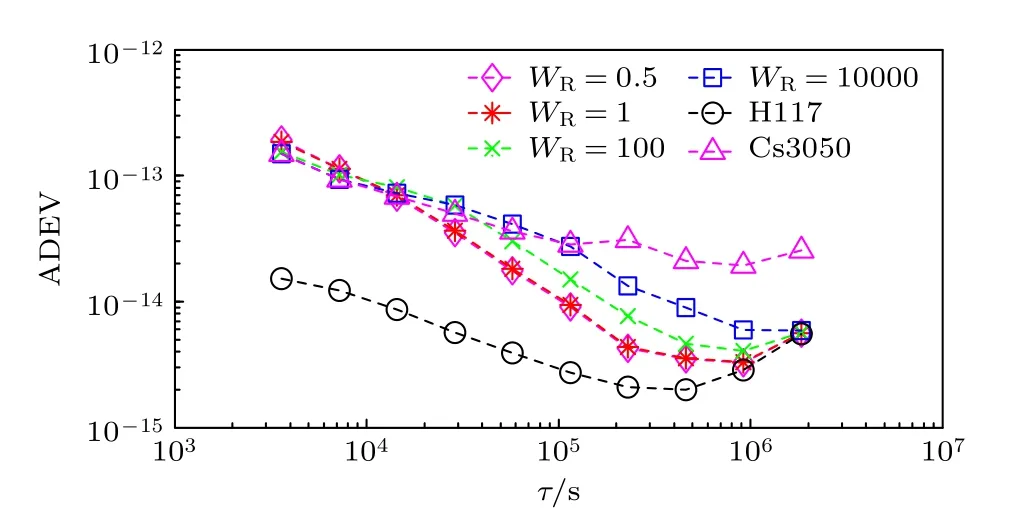
图5 约束矩阵 WR 取不同值时的控制国产钟的稳定度Fig.5.Stability of the controlled domestic clock with different values of the constrained matrix WR .

图6 表示基于不同WR值的控制国产钟相对于参考氢原子钟H117 的稳定度.图中还包括自由运行国产钟的稳定度、参考氢原子钟的稳定度.根据频率标准同步的定义,只要两个频率标准同步,它们之间的相位差就不再发生变化.基于两个频率标准相位差的稳定性分析,相位差的稳定性主要受调相白噪声的影响,这导致在Allan 偏差对数图中斜率为–1,在大范围的平均时间内出现该特性表明控制成功.图6 表明,对于不同WR值,控制国产钟相对于参考氢原子钟H117 的稳定度Allan 偏差图在大范围的平均时间内的斜率近似为–1,对于上述不同WR值,国产钟都能成功地控制到参考钟.并且WR值越小,Allan 偏差图斜率为–1 时的平均时间越小,斜率为–1 的平均时间的范围越大,也就是同步时间越短.图6 表明WR=1/2 时的同步时间最短,WR=104时的同步时间最长.

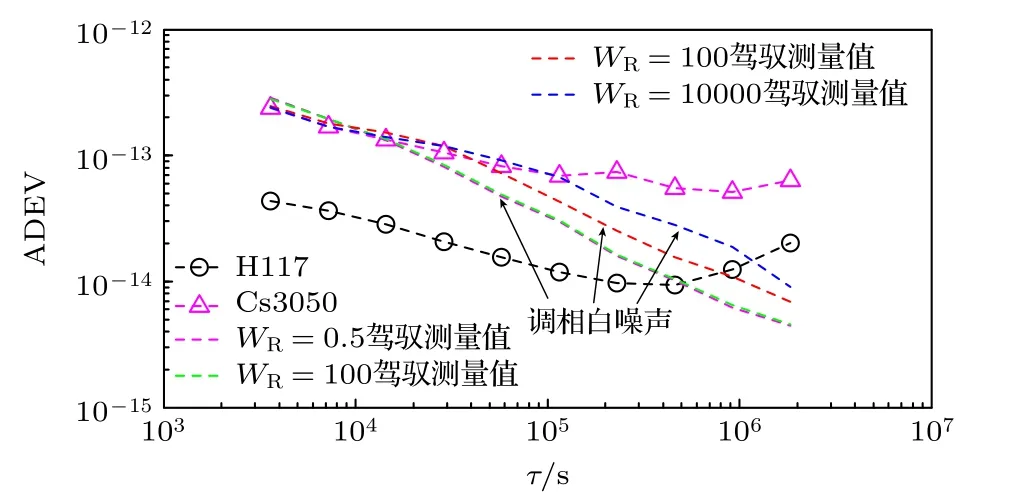
图6 约束矩阵 WR 取不同值时控制测量值的稳定度Fig.6.Stability of control measurement with different values of the constrained matrix WR .

约束矩阵WQ和WR是用来设置控制国产钟状态向量xz,u[k] 和控制向量u[k] 从0 变化时的相对惩罚.一般来说,WQ值不变,WR值增大,对系统的惩罚变大,控制量取到较小的值,系统将状态向量缓慢地控制到0 值附近.系统的同步时间较长,控制原子钟的短期稳定度不受影响,但是控制原子钟的准确度降低.WR值减小,对控制系统的惩罚变小,控制量取到较大的值,系统的状态向量将快速地控制到0 值附近.系统的同步时间较短,控制原子钟的短期稳定度受影响,但是控制原子钟的准确度提高.

3.3 不同控制间隔的国产钟的性能分析

控制间隔也是影响原子钟性能的重要因素.研究不同控制间隔对国产钟的同步时间、控制准确度和稳定度的影响,并给出具体分析.随机选取控制间隔为1,2,4,8 h.约束矩阵随机选取为情况3,即下面具体从同步时间、控制准确度和稳定度方面进行分析.图7 表示不同控制间隔下国产钟的同步时间,可以得出,控制间隔为1 h,同步时间约为5 h.控制间隔为2 h,同步时间约为10 h.控制间隔为4 h,同步时间约为20 h.控制间隔为8 h,同步时间约为28 h.随着控制间隔的增大,同步时间延长.图8 表示同步后不同控制间隔的时间偏差的测量值.为了做图清晰,如前面所述,对测量值加入固定的常数值.可以得出随着控制间隔的增大,控制测量值的随机波动增大,准确度降低.计算控制测量值的3 倍标准差(3σ)评估不同控制间隔下国产钟的准确度,计算结果如表2 所列,控制间隔为1 h,测量值的 3σ为1.83 ns.控制间隔为8 h,测量值的 3σ为4.48 ns.随着控制间隔的增大,准确度降低.

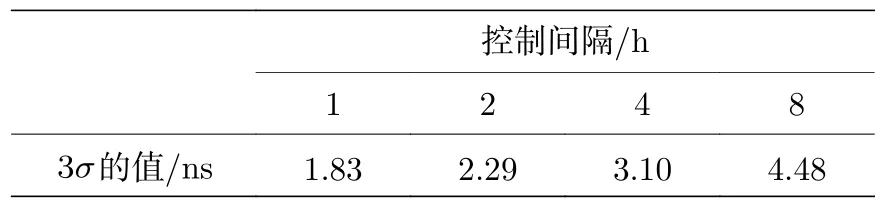
表2 同步后不同控制间隔测量值的3 倍标准差(3σ)Table 2.Three times standard deviation of different control intervals after synchronization.

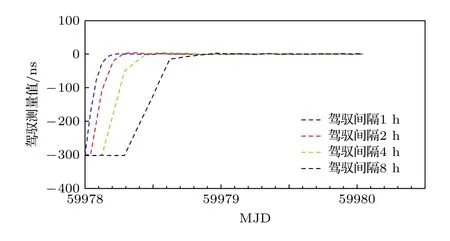
图7 不同控制间隔的同步时间比较Fig.7.Comparison of synchronization time with different control interval.

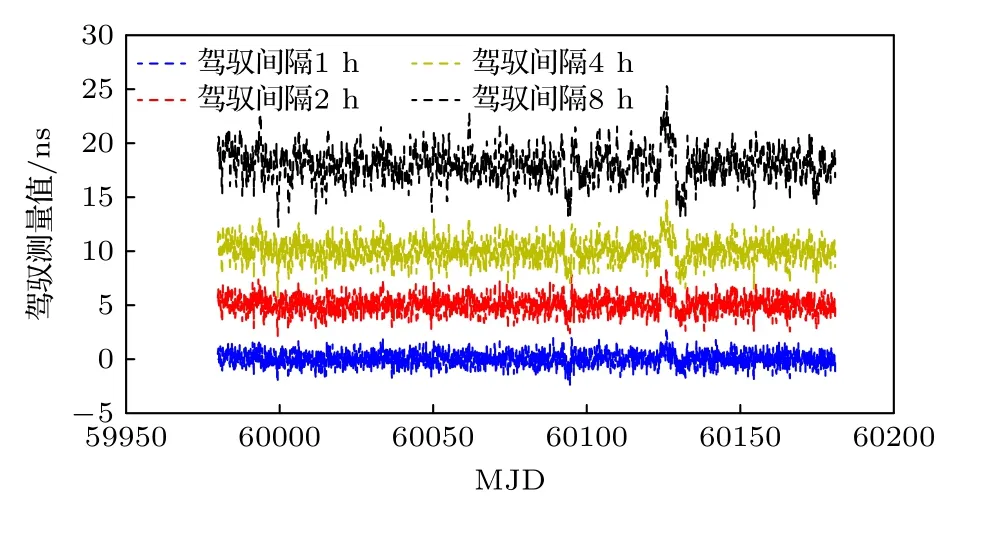
图8 同步后不同控制间隔的测量值Fig.8.Measurements at different control intervals after synchronization.

图9 表示不同控制间隔的国产钟的稳定度,图中还表示了自由运行国产钟Cs3050 的稳定度和参考氢原子钟H117 的稳定度.控制间隔为1 h,国产钟控制平均时间为1 h 的Allan 偏差为1.81×10–13,自由运行国产钟的Allan 偏差为1.48×10–13,说明控制算法使得平均时间为1 h 的稳定度降低,其余平均时间的稳定度得到改善,最后控制国产钟的稳定度服从参考氢原子钟H117 的稳定度.控制间隔为2 h,控制国产钟平均时间为2 h 的Allan 偏差为9.86×10–14,自由运行国产钟的Allan 偏差为9.36×10–14,控制算法对平均时间为2 h 的稳定度影响不大.随着平均时间的延长,控制国产钟的稳定度得到提高,直到稳定度与参考氢原子钟相同.控制间隔为4 h,控制国产钟平均时间为4 h 的Allan 偏差为8.37×10–14,自由运行国产钟的Allan偏差为6.85×10–14,平均时间为1 h 和2 h 的Allan偏差与相应平均时间的自由运行国产钟的Allan基本相同.控制间隔为4 h 主要降低了平均时间为4 h 的国产钟的稳定度,随着平均时间的延长,控制国产钟的稳定度提高,最后与参考钟保持一致.控制间隔为8 h,控制国产钟平均时间为8 h的Allan 偏差为7.55×10–14,自由运行国产钟的Allan 偏差为5.00×10–14,平均时间为1,2,4 h 的Allan 偏差与相应时间的自由运行国产钟的Allan基本相同.控制间隔为8 h 主要降低了平均时间为8 h 的国产钟的稳定度,对于平均时间大于8 h,控制国产钟的稳定度改善,最后达到参考氢原子钟的稳定度.

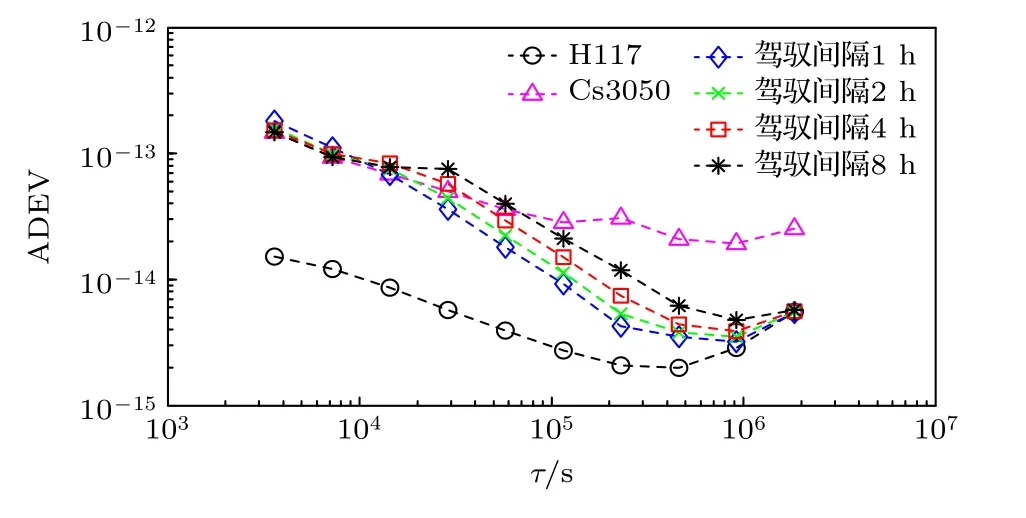
图9 基于不同控制间隔的国产钟的稳定度Fig.9.Stability of the domestic clock based on different control intervals.

图10 表示基于不同控制间隔的国产钟相对于参考氢原子钟H117 的稳定度.图中包括自由运行国产钟的稳定度和参考氢原子钟的稳定度.可以得出,对于不同控制间隔的测量值计算Allan 偏差,较大的平均时间斜率为–1,稳定性主要受调相白噪声的影响,说明不同控制间隔的国产钟都能与参考氢原子钟H117 同步.然而,随着控制间隔的增大,两个时钟之间同步的平均时间出现得较晚,也就是将国产钟控制到参考需要更长的时间.

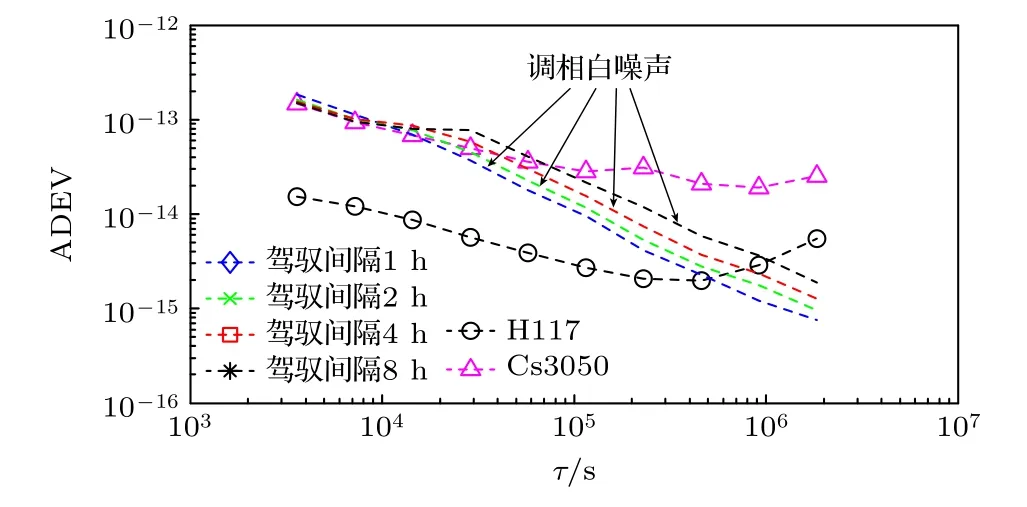
图10 基于不同控制间隔的控制测量值的稳定度Fig.10.Stability of control measurements based on different control intervals.

通过上述分析,当平均时间小于控制间隔时,即τ<τc时(其中τ表示平均时间,τc表示控制间隔),控制国产钟的稳定性受控制过程影响较小,与自由运行国产钟的稳定性相当.在τ=τc时,控制时钟的稳定性较差.当平均时间大于控制间隔时,即τ>τc时,控制国产钟的稳定性就会偏离其自由运行状态.在控制间隔附近,控制国产钟的稳定性收敛到参考氢原子钟之前,通常可以观察到稳定性的波动.然后经过一些平均时间,两个信号的稳定性在Allan 偏差中对齐.

3.4 控制国产钟的长期频率稳定度和漂移率的分析

下面验证本文算法对于国产钟长期频率稳定度和频率漂移的影响,根据3.1 节的氢原子钟测量数据计算时间尺度,选取数据时间段2023 年2 月3日0 时至2023 年11 月30 日23 时,MJD 为59978—60278.96,数据采样间隔为1 h.根据国际权度局(BIPM)每月公布的原子钟速率公报扣除相应的原子钟的速率,结合原子钟每月速率的变化取权重计算时间尺度,测量国产钟Cs3050 与时间尺度的相位偏差.线性二次高斯算法控制国产钟到时间尺度,约束矩阵随机选取为情况3,即WR=1 .根据BIPM 发布的快速协调世界时(UTCr)分别评估控制Cs3050 和自由运行Cs3050 的性能,UTCr 数据为协调世界时每天0 时的测量相位偏差.分别抽取控制国产钟的测量数据和自由运行的国产钟测量数据与UTCr 测量时刻相对应,通过做差得到UTCr 与控制国产钟的相位偏差,UTCr 与自由运行的国产钟的相位偏差,测量间隔为1 d.控制结果如图11 所示,控制国产钟与UTCr 保持在5 ns 以内.长期稳定度如图12 和表3 所示,对于取样间隔为10,20,30,40 d,控制国产钟的Allan偏差明显小于自由运行国产钟的Allan 偏差,说明控制国产钟的稳定度提高,本文算法有效提高了国产钟的长期稳定度.

表3 自由运行Cs3050 与驾驭后Cs3050 相对于UTCr 的频率稳定度Table 3.Frequency stability of free running Cs3050 and controlled Cs3050 relative to UTCr.

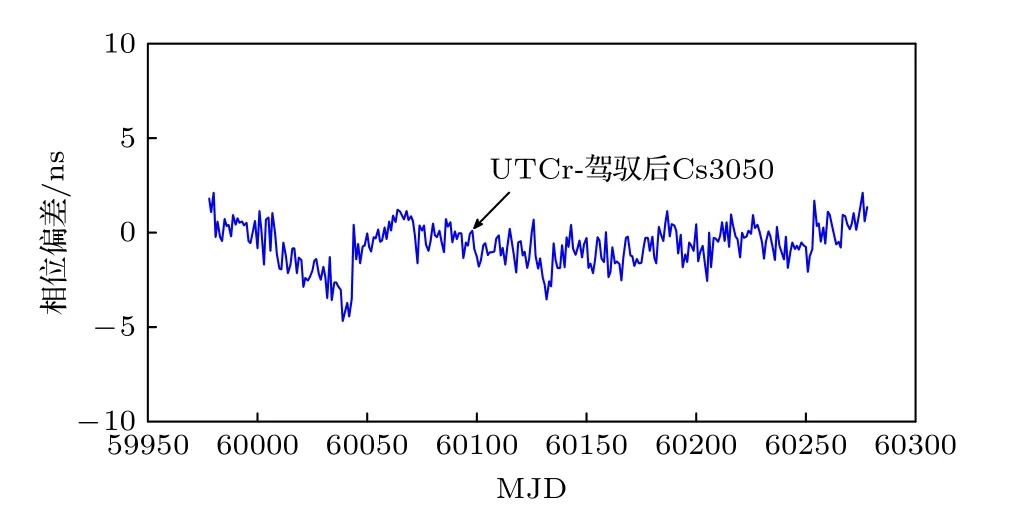
图11 控制后Cs3050 与UTCr 的相位偏差Fig.11.Phase deviation of the controlled Cs3050 from the UTCr.

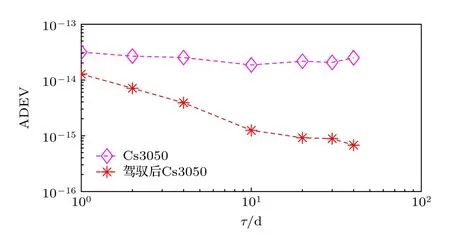
图12 自由运行Cs3050 与驾驭后Cs3050 相对于UTCr 的频率稳定度Fig.12.Frequency stability of free running Cs3050 and controlled Cs3050 relatived to UTCr.

估计控制国产钟的频率漂移,分别以UTCr 为参考估计控制国产钟的频率漂移和自由运行的国产钟的频率漂移.计算周期为30 d,所研究数据共分10 个周期,通过对每个周期相位偏差数据做二次线性拟合估计频率漂移,估计结果如表4 和表5所列.表4 表示自由运行国产钟的频率漂移,表5表示控制国产钟的频率漂移.比较表4 与表5,控制国产钟的频率漂移相对于自由运行国产钟明显降低,说明本文算法有效降低了国产钟的频率漂移.

表4 自由运行 Cs3050 相对于UTCr 的频率漂移Table 4.Frequency drift of free-running Cs3050 with respect to UTCr.

表5 控制Cs3050 相对于UTCr 的频率漂移Table 5.Frequency drift of controlled Cs3050 relative to UTCr.

4 结论

基于噪声类型,研究了国产光抽运小铯钟的控制模型.利用线性二次高斯控制理论,研究了不同约束矩阵条件下的国产光抽运小铯钟的同步时间,控制准确度和稳定度.当二次损失函数中控制量约束矩阵选取较小时,控制国产钟同步需要的时间短,控制国产钟的准确度高,但是短期稳定度较差.当二次损失函数中控制量约束矩阵选取较大时,控制国产钟同步需要的时间较长,控制国产钟的准确度降低,但是短期稳定度高,与自由运行国产光抽运小铯钟的短期稳定度相当.因此结合文中的研究结果,选取适合的约束矩阵以满足实验室需求的守时指标,比如同步时间、控制准确度和稳定度.

基于国产光抽运小铯钟的控制模型,研究了不同控制间隔的钟的性能.对于不同的控制间隔,本文给出了国产光抽运小铯钟的同步时间,控制准确度和稳定度.对于较小的控制间隔,需要的同步时间较短,控制准确度高,但是短期稳定度降低.对于较大的控制间隔,需要的同步时间较长,控制准确度降低,但短期稳定度高.根据实测数据,给定控制间隔范围内,控制准确度优于5 ns.控制后的中长期稳定度得到改善.

根据实测数据,基于最优控制理论的国产光抽运小铯钟频率控制算法的研究结果,当约束矩阵控制间隔为2 h,控制准确度为2.29 ns,短期稳定度接近自由运行国产光抽运小铯钟,中长期稳定度得到明显提高,能够较好地满足各项守时指标.