基于构网型储能的风电场-弱电网次同步振荡抑制方法

伍双喜,王晰,刘洋,Jan Shair,向丽玲,谢小荣

(1. 广东电网有限责任公司电力调度控制中心,广州市 510600;2. 新型电力系统运行与控制全国重点实验室(清华大学电机系),北京市100084)

0 引 言

伴随电力系统的“双高”特征日益显著,以风电、光伏为代表的变流器接口发电(converter interfaced generation, CIG)在电源结构中占据的比例逐渐提升,深刻地改变了电力系统的物理特性和稳定机理。风、光等资源本身的波动性和间歇性、高比例电力电子装备引发的多时间尺度动态等特点,使得电力系统面临多种新型稳定性问题,如“类机电”低频振荡、宽频电磁振荡、新能源机组的大扰动稳定性等[1]。其中,宽频振荡及其包含的次同步振荡(subsynchronous oscillations, SSO)即是一例典型问题。SSO常由CIG控制环节和交直流电网间的动态相互作用引起,可使系统电压/电流出现数Hz至两倍工频范围的非特征分量。不利条件下,次同步分量会持续增长乃至超过工频分量,导致新能源机组损坏、脱网甚至全局性安全问题;相关事故已在国内外被多次发现和报道[2-3]。

目前抑制次同步振荡的方法大致分源侧和网侧两个角度。在电源侧,通常对机侧或(和)网侧变流器的控制策略做针对性的改进——多为附加次同步阻尼控制器(subsynchronous damping controllers, SDC)或优化变流器控制环节的部分参数[4]。由于电源侧的控制通常可重塑机组在次/超同步频率范围的幅频相频特性,因而也被称为阻抗重塑控制[5]。但实际风电场中机组数量众多、位置分散、型号各异,逐一修改或调整其控制模块将带来繁重的工作量,可行性较差。在电网侧,依据振荡发生的不同场景,陆续有学者挖掘了柔性交流输电系统(flexible AC transmission system,FACTS)控制器[6]、柔直换流器[7-8]等装置的潜力,将静止无功补偿器(static var compensator, SVC)[9]、统一潮流控制器(unified power flow controller, UPFC)[10-11]、静止同步补偿器(static synchronous compensator, STATCOM)[12-13]等设备安装在风电场并网点处,实现次同步振荡的主动阻尼控制。

近年来,电池储能系统(battery energy storage system, BESS)因其在“双高”电力系统中的关键作用广受关注。BESS提供的服务包括负荷调节、调峰、调频、应急供电等,也可作为电网侧主动阻尼控制的方法之一。文献[14]指出,通过储能实现有功功率的灵活调节,能有效防治跨区输电中的低频振荡问题。类似地,亦有研究证实BESS能降低风电场并网的电磁暂态过程引发SSO的风险:文献[15]使用添加有源阻尼控制的储能变流器,抑制了风机和电网的次同步相互作用;文献[16]通过BESS在次同步频率范围内增加了双馈风机-串补网络的虚拟阻抗;文献[17]通过优化构网型储能的控制结构参数,实现了一定干扰度范围内的频率稳定和同步稳定。

本文使用附加次同步阻尼控制的构网型电池储能系统(grid forming-battery energy storage system, GFM-BESS)抑制直驱风电场并入弱电网引发的SSO。本文的主要贡献包括以下三点:

1)提出了一种更加简单实用的对现有构网型储能变流器控制策略的修正:将2个次同步阻尼控制器作为附加回路,并联连接到GFM-BESS的电流控制内环。

2)比较了三种SDC的阻尼性能和BESS容量对SDC阻尼效果的影响。

3)通过电磁暂态仿真验证了这一控制策略的可行性。

本文第1节介绍了所构建的直驱风机-电池储能系统概况;第2节详细讨论了使用基于构网型控制策略的SDC抑制SSO的方法;第3节展示仿真结果和对应分析;第4节总结归纳全文。

1 风电场-BESS接入交流电网模型

1.1 系统概况

考虑在风电场配套安装电池储能的情景,所构造的系统模型如图1所示,装机容量200 MW的直驱风电场和10 MW的BESS升压后共同接入230 kV交流母线。BESS在平滑风电出力波动的同时,可参与调频、黑启动等辅助服务。系统参数见表1。

表1 系统参数

图1 直驱风电场-BESS接入弱交流电网系统示意图

风电场并入的交流电网强度较低时,会存在次同步振荡的风险。阻抗分析是识别系统中存在振荡模式的常用方法。在图1所示系统中,电网、传输线和变压器的阻抗参数一般可作为给定值获取,故而能计算出它们确切的阻抗矩阵解析式ZT1(s)、ZT2(s)与Zg(s)。而风机和BESS的控制结构常为“黑/灰箱”,阻抗参数难以直接获取。本文参考文献[18]提出的基于实测的阻抗模型辨识方法,通过注入不同频率的小扰动信号,经过各离散点数据的整理和拟合,求得风电场和BESS的频率耦合阻抗模型ZWF(s)、ZBS(s)。另外,综合考虑风电和BESS并网前的滤波、升压等环节,需对ZWF(s)、ZBS(s)作适当修正(修正后的阻抗矩阵用ZWF-r(s)、ZBS-r(s)表示);二者与交流电网的阻抗相加,得到全系统的聚合阻抗矩阵ZΣ(s)。

ZΣ(s)=ZWF-r(s)+ZBS-r(s)+Zg(s)

(1)

通过分析ZΣ(s)矩阵元素,可证明存在相互耦合的次/超同步振荡模式。

采用短路比(short-circuit ratio, SCR)衡量电网强度,并模拟了仿真系统中次同步振荡发生的过程。根据定义,计算得到图1所示系统的短路比σ:

(2)

式中:U2为并网点连接的交流母线电压;Xg为并网点处的网络等效电抗;SW、SB分别表示风电场内的直驱风机容量与安装的储能电池容量。

由于电网电压U2和装机容量SW、SB均为常数,因而仿真时只需改变交流电网的等效电抗Xg,即可改变短路比,实现电网不同强度的模拟。SCR的初始值设定为4;在4 s时降低至临界短路比以下的1.91以引发次同步振荡。从时域、频域的电流波形(图2、图3)可看出,t=4 s后振荡开始产生,且振幅逐渐增加使变流器的控制环节进入饱和;电流中同时存在相耦合的次/超同步分量,频率为45/55 Hz。

图2 发生不稳定SSO后,风电场和BESS的电流、有功功率波形图

图3 电流经FFT变换后的频谱分析图

1.2 BESS的结构与控制

电池储能系统主要由电池组、直流/直流(DC/DC)变换器,直流/交流(DC/AC)变流器三部分组成。其中DC/DC变换器的基本拓扑常使用双向Buck-Boost电路,采用恒定直流母线电压或恒定直流功率控制策略;DC/AC变流器使用三相全桥电路,含有功功率、无功功率、直流侧电压等控制环节。储能系统的主电路基本结构如图4所示。

图4 储能系统的主电路结构示意图

由于电池组和DC/DC变换器中电能形式均为直流,在次同步振荡的分析中不起作用,因而可以将二者合并简化为一恒压源(假设直流电压控制能保证DC/DC始终输出稳定的电压)。

BESS中DC/AC变流器的控制方式可以选择跟网型(grid-following, GFL)或构网型(grid-forming, GFM);前者需锁相环测量并网点的相位信息以实现同步;后者则仿照了发电机的功率同步原理,具体实现方法包括下垂控制、虚拟同步机控制、匹配控制、虚拟振荡器控制等。在弱交流电网、孤岛供电等场景下,GFM模式的适用性更强[19]。在本文搭建的构网型电池储能系统中,变流器采用虚拟同步机(virtual synchronous machine, VSM)策略,整体结构如图5所示[20]。VSM由有功-频率控制(原动机控制)、无功-电压控制(励磁控制)、虚拟导纳控制、电流内环控制四部分组成。构网型储能变流器控制参数取值如表2所示。

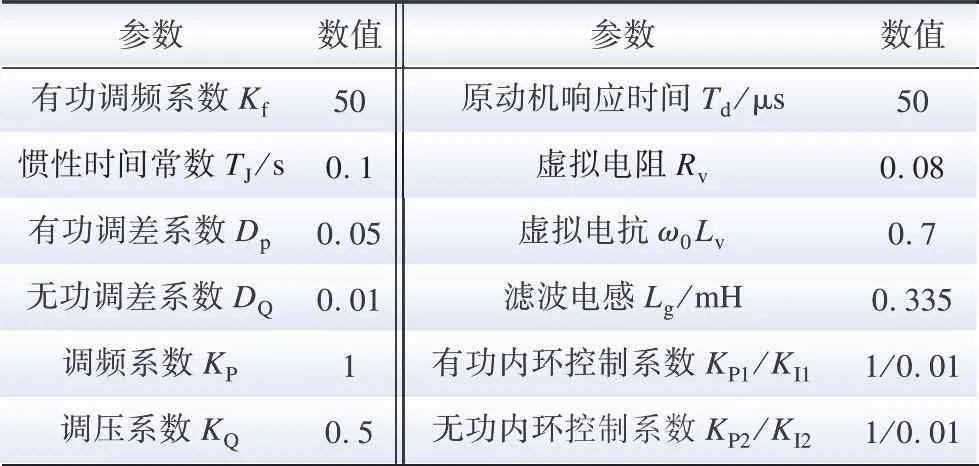
表2 构网型储能变流器控制参数

图5 构网型控制策略的基本结构

在VSM策略中,虚拟导纳控制相当于在逆变器的输出端口串接一个等效阻抗。其中的电抗分量解耦变流器的有功、无功控制回路,抑制高次谐波;电阻分量可调整变流器的阻尼和动态特性,也能减小短路时的冲击电流。电流内环控制的作用包括提高整体响应速度、过流保护、改善逆变器输出电能的质量等;并且相较于响应稍慢的外环(有功、无功)控制,电流环的存在能够保证合理的控制速度[21]。

2 SDC的设计与分析

2.1 设计原理

并网条件下,构网型BESS具有更小的振荡风险;对两种模式变流器的阻抗分析表明,跟网型变流器在次/超同步频段相对更易表现为负电阻特性和容性效应,小扰动稳定性能与构网型变流器相比稍差。这一自身禀赋的优势,使GFM-BESS能够高效减少其电力电子接口与风电场、交流电网相互作用引发振荡的潜在风险。

尽管如此,GFM-BESS仍需添加相应的阻尼控制模块,以求在自身稳定性较高的基础上进一步提升振荡阻尼能力,保障并网系统的稳定性。如前文所述,这一功能常通过在变流器控制部分添加SDC实现。此外,由于系统内的超同步振荡分量是受次同步分量耦合而出现,因此只需对45 Hz的次同步振荡模态进行抑制,即可达到预期效果。

SDC可采用多种控制结构,如并联比例-微分控制器、串/并联陷波滤波器[22]、具有控制增益的超前-滞后控制器[23],或者更复杂的比例谐振控制[24]、滑模控制[25]、H∞控制[26]等。本文考虑SDC的3种可行的设计:基于低通滤波器(low pass filter-SDC, LPF-SDC)、基于陷波滤波器(notch filter-SDC, NF-SDC)和基于移相环节(phase shift-SDC, PS-SDC)。三者的传递函数为:

(3)

(4)

(5)

式中:式(3)表示以ωl为中心频率的二阶低通滤波器;式(4)表示以ωn为陷波频率的二阶陷波滤波器的中心频率,同时附加有一定的相移;式(5)表示超前(滞后)时间常数分别为T1(T2)的移相滤波器;ζ是滤波器的阻尼系数;Kg是控制器增益。

三种SDC的控制流程框图如图6所示。

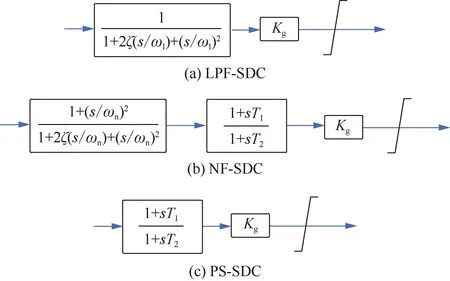
图6 SDC的三种结构

对于以上三种次同步阻尼控制器,LPF-SDC可以去除低于某一特定频率值的振荡成分;NF-SDC旨在直接消除系统内的目标振荡频率,常用于处理高频振荡问题。而PS-SDC通过滞后-超前环节改变系统相位,可被视为虚拟阻抗;当虚拟阻抗能够在次同步频率下提供正的等效电阻,即能实现对SSO的抑制。PS-SDC带来的相移由时间常数T1、T2和控制阶数所决定。一般而言,因为其自身结构难以去除振荡中的高频成分,基于移相器的次同步阻尼控制更适合解决频率稍低的振荡问题。

2.2 SDC的参数取值与添加位置

参数取值方面,LPF-SDC与NF-SDC的阻尼系数ζ均取0.707。低通滤波器的中心频率ωl设置为2倍工频(100 Hz)以滤除高频噪声;陷波频率ωn设置在与SSO频率互补的位置(工频减去振荡频率)。为简便起见,本文假定ωn为一固定值,使陷波频率和SSO频率始终能够匹配。但实际中有关振荡参数往往难以提前获知,需要在线测量或估计;这种情形下应当配置自适应频率变化的控制器[27],无需在工况变化后重新调整和选择滤波器参数。下面以PS-SDC为例,简单阐述自适应振荡频率的次同步阻尼控制器参数整定流程。

本文2.1节中已介绍过PS-SDC的基本原理。对于采用移相环节结构的控制器,核心在于保持符合要求的总相移大小以使次同步频率下的等效阻尼为正。在信号从输入到输出的全部流程中,用于提取振荡信号的滤波器(位于图6描述的SDC之前,滤除噪声等无关分量)也会引起一定的相位延迟。因此,系统的相移总共由两部分组成:

φreq=φtotal=∠HPS-SDC(s)+φfil

(6)

s=j2πfsub

(7)

式中:φreq代表系统所需的相移(同时也是系统总的相位偏移值φtotal);φfil代表滤波器引入的相移;fsub代表发生次同步振荡的频率。

简便起见,令式(5)表示的移相控制器的传递函数中Kg= 1,T2= -T1=T,则通过计算可以得到:

(8)

为确保PS-SDC始终起到正阻尼的作用,系统总相位变化需保留一定的裕度。如φreq设置为80°,以避免总相移超出90°的情形下控制器反而在次同步频段呈现负电阻特性,促进振荡的发生和增长。

添加位置方面,SDC安装在GFM控制环节的部位将决定BESS对次同步振荡的整体抑制性能。如本文1.2节所述,控制外环的响应速度较慢而内环响应速度更快,因而在电流控制环中添加阻尼控制器的效果通常较好。文献[22]以双馈风电机组源、网两侧的变流器(采用跟网型控制)为研究对象,比较了在变流器电流控制环的不同位置添加次同步陷波器的阻尼性能。

本文将SDC和电流控制环内的滞后校正环节相并联,如图7所示。SDC的输入来自VSM的d、q轴输出电流;输出与计算得到的d、q轴参考电压相加,经PWM调制生成逆变电路的控制脉冲序列。

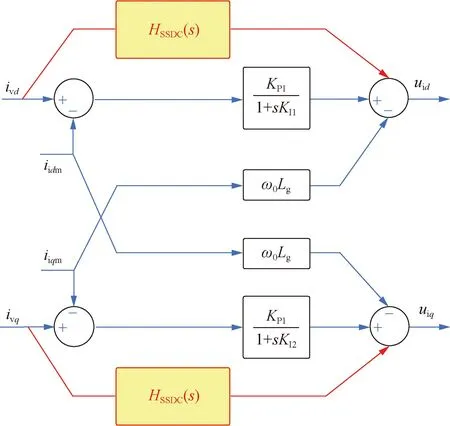
图7 电流控制环嵌入SDC的示意图

3 仿真结果分析

3.1 电磁暂态仿真结果

按照本文第2节提出的3类SDC设计结构,在Matlab/Simulink中搭建对应的控制模块并进行仿真。图8—10分别展示了在构网型储能变流器的控制环节增加LPF-SDC、NF-SDC、PS-SDC后,并网公共连接点处线电流和有功功率的波形。

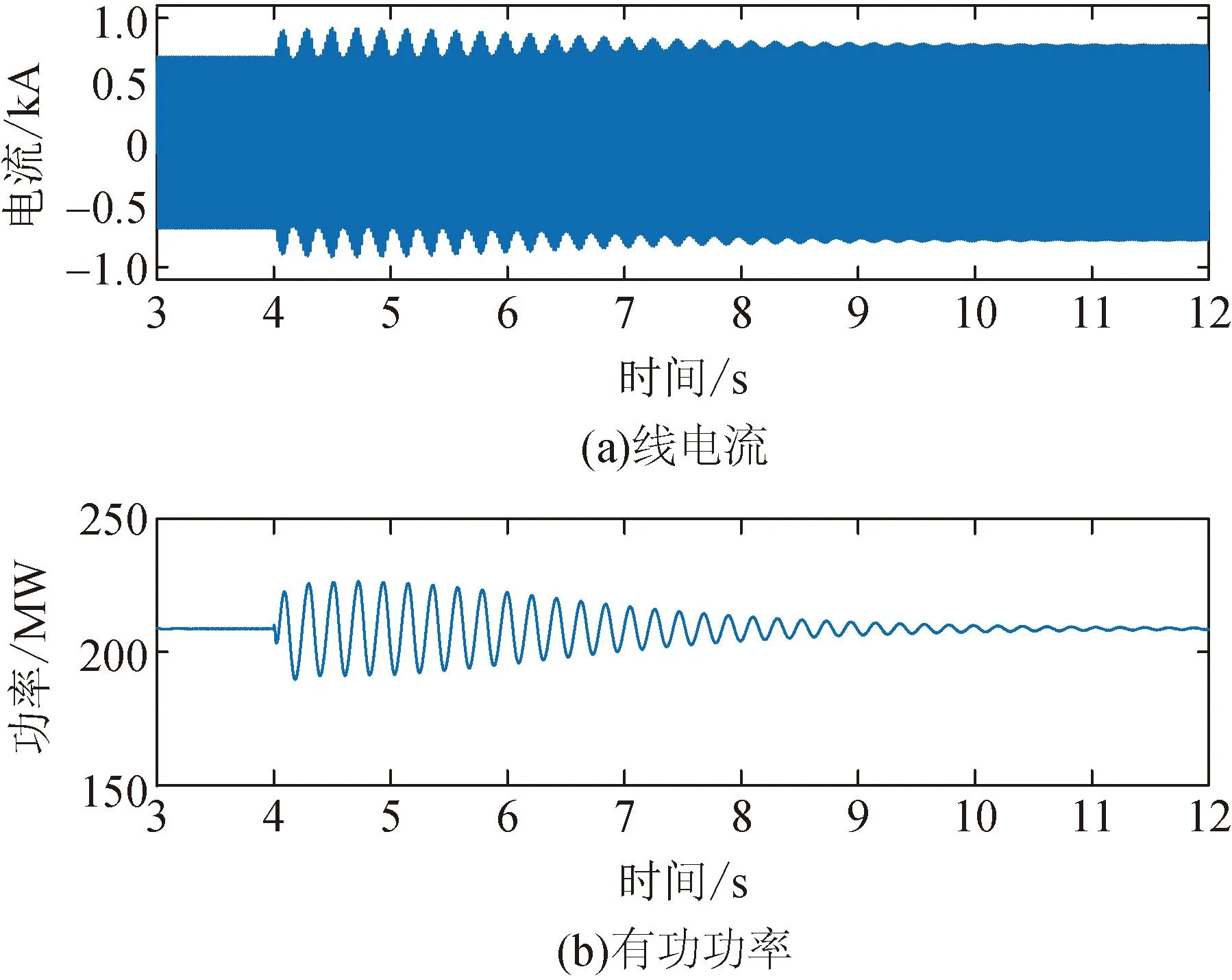
图8 GFM-BESS中添加LPF-SDC后的线电流和有功功率波形

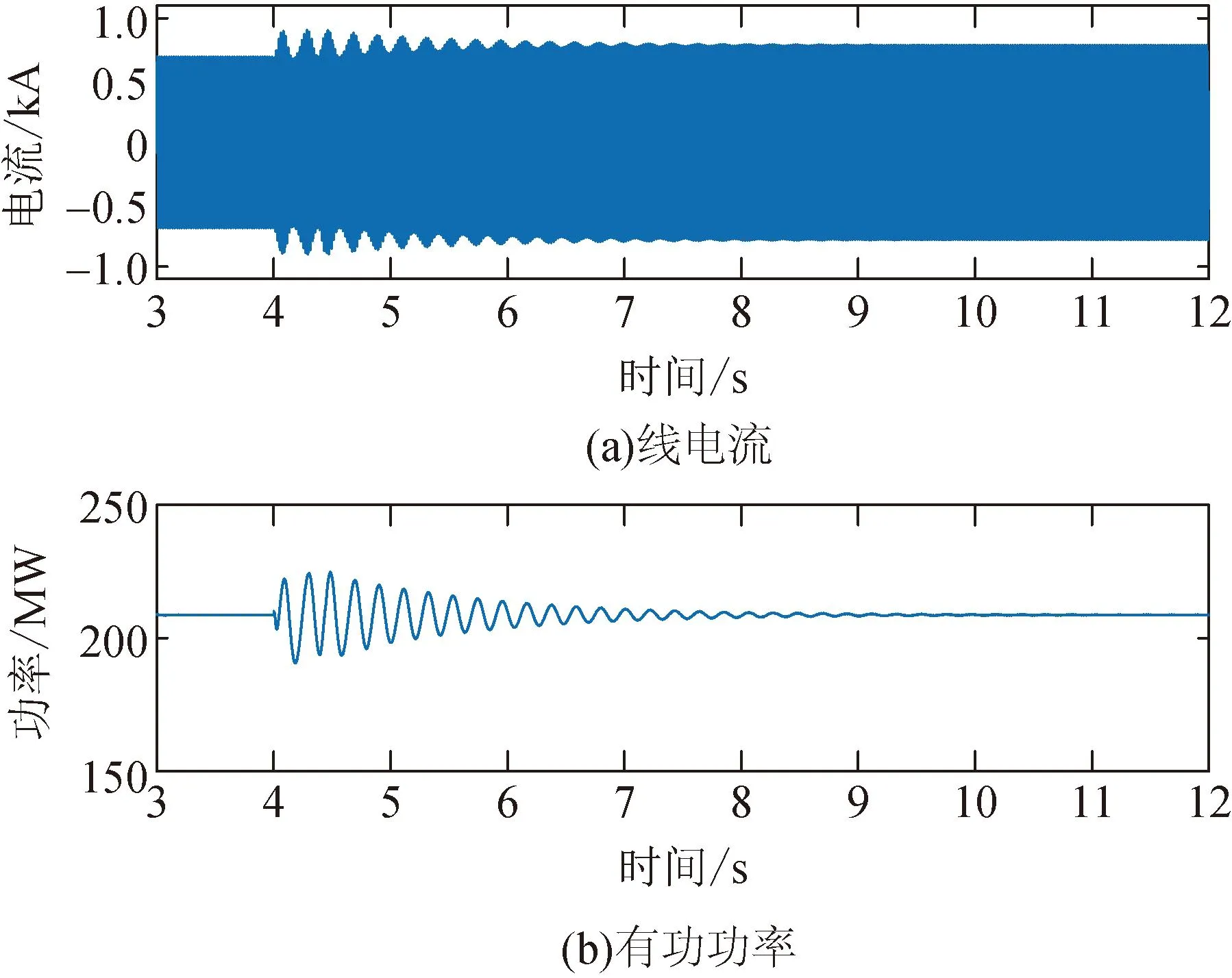
图9 GFM-BESS中添加NF-SDC后的线电流和有功功率波形

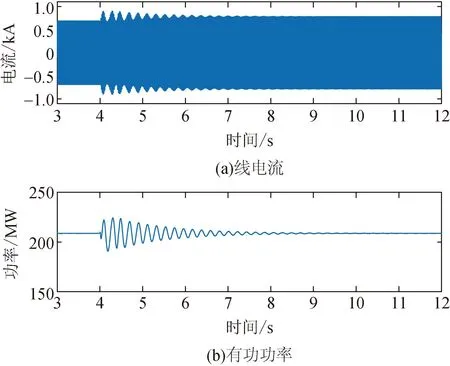
图10 GFM-BESS中添加PS-SDC后的线电流和有功功率波形

从仿真结果中不难发现,本文所设计的3种次同步阻尼控制器均可达成有效抑制SSO、维持系统安全稳定的预期效果。在振荡发生后的5～7 s内,45 Hz/55 Hz非工频分量基本衰减完毕。同时,图11展示了添加PS-SDC后电流控制环的输入-输出情况:d、q轴的电流曲线均显示,PS-SDC能够实现输出与输入物理量间的90°相移。

图11 PS-SDC实现输出与输入电流间的90°相移

图12则更细致地比较了不采取任何措施和分别投运三种阻尼控制器后的有功功率变化曲线。对三种SDC的比较表明,所采用的仿真工况下,PS-SDC和NF-SDC抑制次同步振荡的效果大致相近,且投运后的振荡幅值、衰减速度等指标均优于LPF-SDC。因此,在本文构建的直驱风电场-弱交流电网系统中,基于陷波器和基于移相器的SDC是抑制振荡的更优选择。但值得注意的是,本例的对比结果并不能够代表SDC选型的普遍规律:如前所述,不同种类的SDC存在适配场景上的差异,如NF-SDC更多用于治理高频振荡而PS-SDC偏向于低频,实际工程中的控制器选型必须结合现实情境与振荡特点。

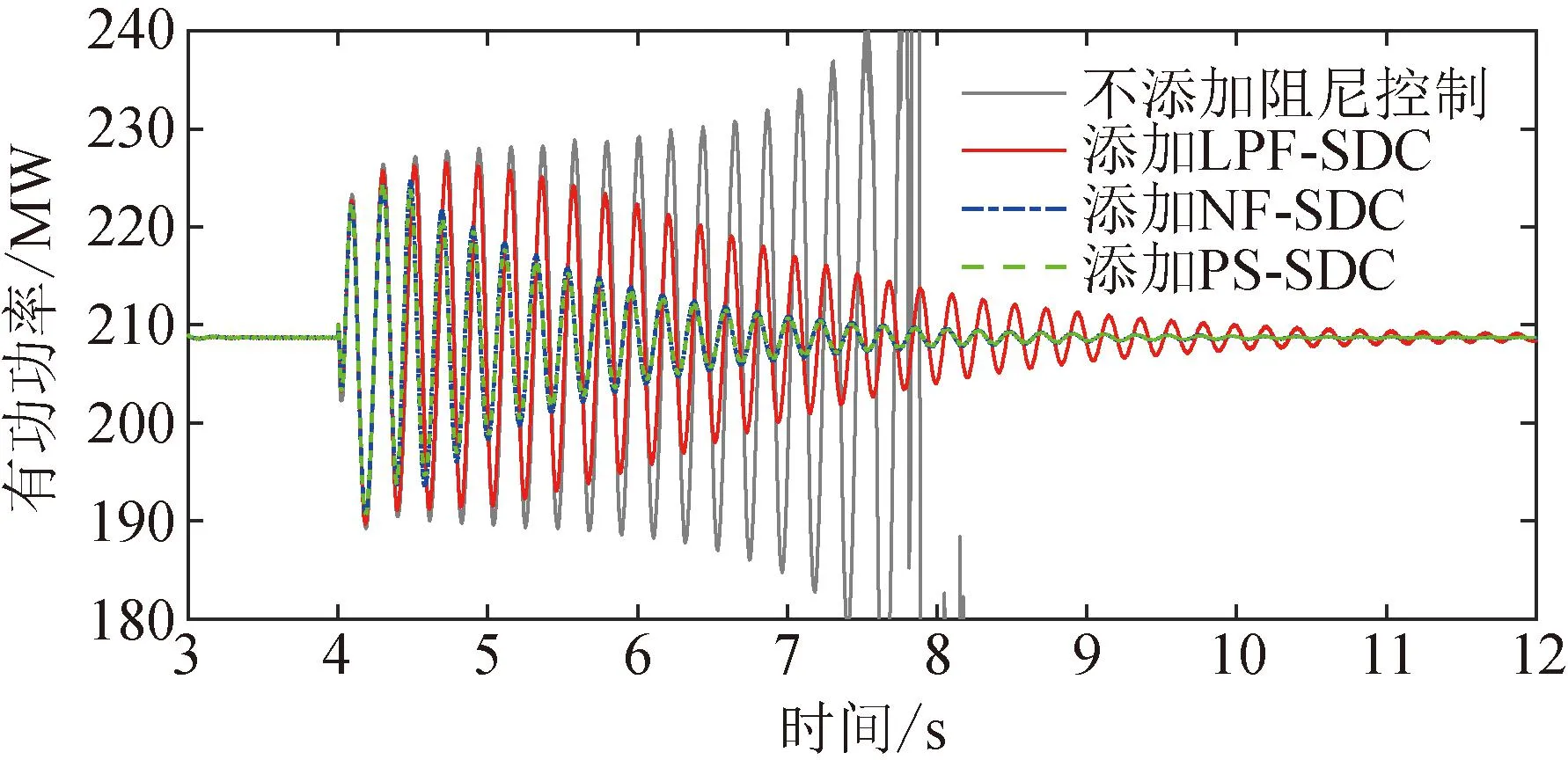
图12 三种SDC阻尼效果的展示与对比

3.2 BESS容量对阻尼效果的影响

针对配备电池储能系统应对SSO风险的方法,已有文献指出储能系统的容量会和风电场的接入容量一样影响对不稳定振荡模式的阻尼效果[28];因而,风电场配套BESS容量也需经过合理的优化设计。

在本文所研究的风电场-BESS系统中,BESS容量为风电装机容量的5%(10 MW)。该设置是综合考虑风电场的多种运行工况,按振荡风险最严重的额定工况(即所有机组全部投运,出力达到额定值)通过分析选取的。该工况下功率最大、电网相对强度最低,振荡风险最严重[29];该最严重情况下GFM-BESS能有效发挥振荡抑制作用,自然可以应对其他危险性相对轻的情形。

图13以NF-SDC为例,展示了不同储能容量下的仿真波形。结果表明,若储能容量小于10 MW,则其提供阻尼的作用将受到削弱。当BESS容量为风电场装机的4%(8 MW)时,振荡衰减系数仅为0.470,系统需10 s以上才能结束过渡过程回到稳态,时间相较5%的情形大大延长。而在容量减小至3%(6 MW)时,GFM-BESS已经不足以有效地抑制振荡,SSO仍呈现发散趋势。根据工程需求和所建系统的实际情况,我们期望GFM-BESS能于10 s内完成SSO的高效抑制,而8 MW的容量取值并不能满足这一预期。可见,5%(10 MW)基本是使系统符合上述SSO治理要求的最小值;只有5%及以上的BESS容量方可使系统阻尼达到预期目标,进而实现次同步振荡的快速抑制。

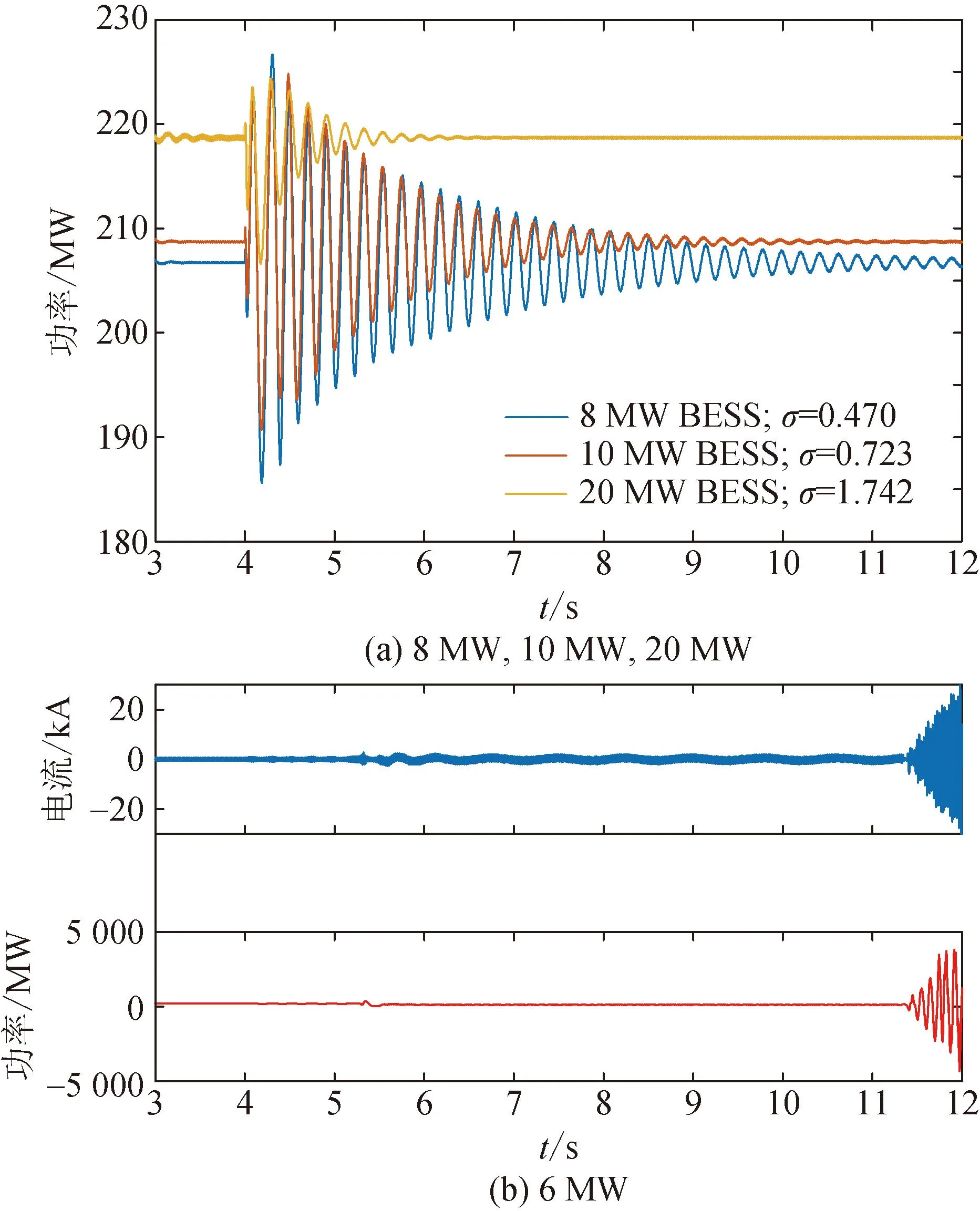
图13 不同BESS容量对SSO抑制效果的影响

相应地,若适当增加储能容量(如增至风电场容量的10%),则阻尼效果将更为显著。当然,也不可为片面追求绝对的安全稳定而盲目配置远大于实际需求的储能设施,造成利用率低下和设备冗余;BESS容量的选择需要对新能源机组出力、当地负荷水平、稳定运行要求、投资和运维的经济性等多元因素进行综合权衡与研判。

通过比较不同出力工况下振荡发生后的有功功率曲线,也可以验证5%储能容量配置的有效性。图14展示了风电出力为额定值的20%、60%、80%和100%的情形下振荡发生前后的功率变化情况。除20%工况下的功率波动本身即处在稳定模态之外,在其余3种工况中BESS均起到了理想的SSO抑制作用。

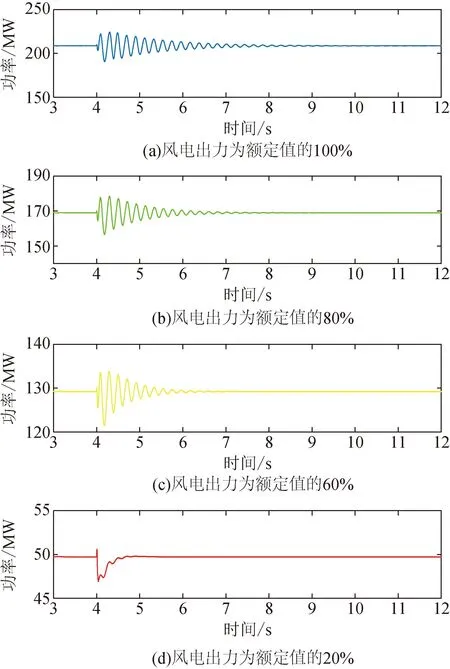
图14 不同工况下GFM-BESS对SSO的抑制效果

4 结 论

本文采用构网型控制的电池储能系统抑制直驱风机和弱交流电网相互作用引发的次同步振荡,为“双高”电力系统中高比例电力电子变流器设备带来的宽频振荡风险提供了一种经济高效的防范措施。主要结论如下:

1)在GFM-BESS变流器的电流控制环中添加SDC,可在次同步频率范围内提供正阻尼,实现对次同步振荡的有效防治。

2)SDC结构的选择上,采用二阶陷波滤波器并结合移相环节的NF-SDC和基于移相器的PS-SDC在所构建的系统条件下具备更优越的性能。

3)通常5%的BESS容量即能为SSO抑制提供足够的阻尼;适度提高BESS的容量可增强对SSO的抑制效果。

在本文内容的基础上,未来可针对风电场引发宽频振荡的自适应抑制、储能变流器容量规模的定量优化、储能装置多元功能的协同控制等更深层的问题展开研究。