基于线性自抗扰控制的双馈风机次同步振荡抑制研究

程启明,周伟成,程尹曼,张磊

(1.上海电力大学自动化工程学院,上海市 200090;2.国网上海市电力公司市北供电分公司,上海市 200041)

0 引 言

风电装机和并网容量不断增大,同时我国风能集中区域与电力负荷集中区域相距较远,为提高线路的传输能力,电力系统通常在输电线路上加入串联补偿设备[1]。而双馈风力发电机(doubly-fed induction generator,DFIG)通过串补线路传输功率时不容忽略的问题就是次同步振荡(sub-synchronous oscillation,SSO)[2]。

2000年以来SSO引发的电网事故在逐渐增多,2009年美国德州发生大量风电机组脱网及crowbar损坏的SSO事故[3];2012年底我国华北一集群风电场机组网侧电流中含有6～8 Hz次同步频率分量,导致部分风机脱网[4]。经研究表明,DFIG风力发电中的此类问题主要由风电控制器与外部串补的线路耦合引起,即次同步控制相互作用(sub-synchronous control interaction,SSCI)。不同于火电厂SSO问题,其与轴系模态无关,发散速度更快,危害更严重[5-7]。SSCI的振荡频率具有时变特性,其不仅与电力系统线路结构和风机控制器有关,也随风电场的运行状态进行波动[8]。

风电系统SSO问题相较于传统火力发电,其振荡机理和抑制措施都处于探索阶段。文献[9]表明风电系统次同步稳定性与风速成正比,与转子侧变流器(rotor-side converter,RSC)中电流环比例系数和线路串补度成反比。目前主要的抑制策略主要有两大类:一是电网侧附加灵活交流输电系统(flexible alternating current transmission system,FACTS)装置。文献[10]设计并验证了一台次同步抑制设备;文献[11]使用电力系统稳定器(power system stabilizer,PSS)和静止无功补偿器(static var compensator,SVC)联合作用来抑制次同步主谐振点的振荡;文献[12]使用统一潮流控制器(unified power flow controller,UPFC)来增强系统对次同步阻尼效果。但这类方法加设额外硬件装置使得控制复杂度和成本上升。二是风机侧优化变换器结构、优化控制方法或调整控制参数。文献[13-14]提出附加阻尼控制方法(supplementary sub-synchronous damping controller,SSDC)利用基于次同步电流的变化控制信号,修正对应的输出电压。但是SSCI谐振频率具有时变性,工况改变时其中移项环节以及滤波参数不再适用。文献[15]表明选择合适的控制参数可有效抑制SSO发生,但是改变变流器的参数可能影响其原有的控制性能,比如减小转子侧内环比例系数会导致控制器的电流跟踪效果下降。文献[16-20]将传统比例积分控制更换为部分反馈线性化控制器、滑模控制、H∞等先进的非线性控制器,其需要风机的精确建模,且计算复杂、参数整定困难,工程难以实践。

自抗扰控制(active disturbance rejection control,ADRC)是韩京清教授提出继承传统PID控制技术优点同时不依赖于被控过程模型的控制方法。其主要功能组成为:使输入平滑的跟踪微分器(tracking differentiator,TD)、估计补偿内外总扰动的扩张状态观测器(extended state observer,ESO)、非线性状态误差反馈(nonlinear state error feedback,NLSEF)和扰动估计补偿。对于系统运行工况多变情况,ADRC参数有着很强的鲁棒性。

同理对于随机性强的风电系统,ADRC对其时变的SSCI依然适用。而在次同步频率下,控制环节会通过转子侧换流器向系统的电气谐振提供额外的负阻尼,其中影响转子等效阻抗比重最大的是其有功内环PI的电流跟踪比例系数KP。可以通过ADRC阻断RSC与串补线路之间耦合作用来抑制SSCI。但是ADRC中NLSEF和ESO环节以非线性函数呈现,使得实际工程中难以对ADRC参数整定和性能分析。

文献[21]提出线性化、带宽化的线性ADRC(linear ADRC, LADRC),其参数整定简单、具有明确物理含义,同时保留了对复杂非线性不确定系统的良好控制能力[22-24]。因此,本文以ADRC为基础,引入基于双馈风机模型线性ADRC控制理念,设计一种不影响DFIG正常运行稳定又能针对SSCI时变谐振频率特性的控制器。基于上述情况,本文建立DFIG经串补线路接入无穷大系统的数学模型,在此基础上研究DFIG系统SSCI问题的机理。提出使用线性ADRC取代传统内环PI控制,来抑制转子侧SSCI扰动的策略,其中通过扩张状态观测器实时估计次同步振荡分量,并通过线性状态误差反馈(linear state error feedback,LSEF)和扰动估计进行补偿。在Matlab/Simulink平台上搭建DFIG风电场经串补线路外送功率的模型来研究SSCI抑制策略,通过与PI控制的抑制效果对比,验证该控制策略在稳态和暂态拥有良好的控制性能;通过与附加阻尼控制对比,验证线性ADRC可以在多工况下抑制次同步振荡;最后与非线性ADRC对比,验证其参数整定的简便性。最后在RT-LAB半物理实验平台对上述控制策略进行进一步验证。

1 DFIG建模与SSCI机理

1.1 DFIG数学模型

DFIG风力发电系统的主体是风机、齿轮、DFIG、背靠背变流器。考虑转子侧网侧变换器间通过直流母线和大电容而解耦,故可实现分别单独控制。网侧变流器(grid-side converter,GSC)的作用是保证输入电流波形正弦性,维持直流母线电压稳定;RSC主要给DFIG转子绕组提供交流励磁,并对定子输出有功和无功解耦控制[25]。

在理想条件下,即气隙磁场按照正弦规律分布、忽视漏饱和、三相绕组对称,实际电机绕组可等效成图1所示的三相双馈异步风力发电机物理模型。

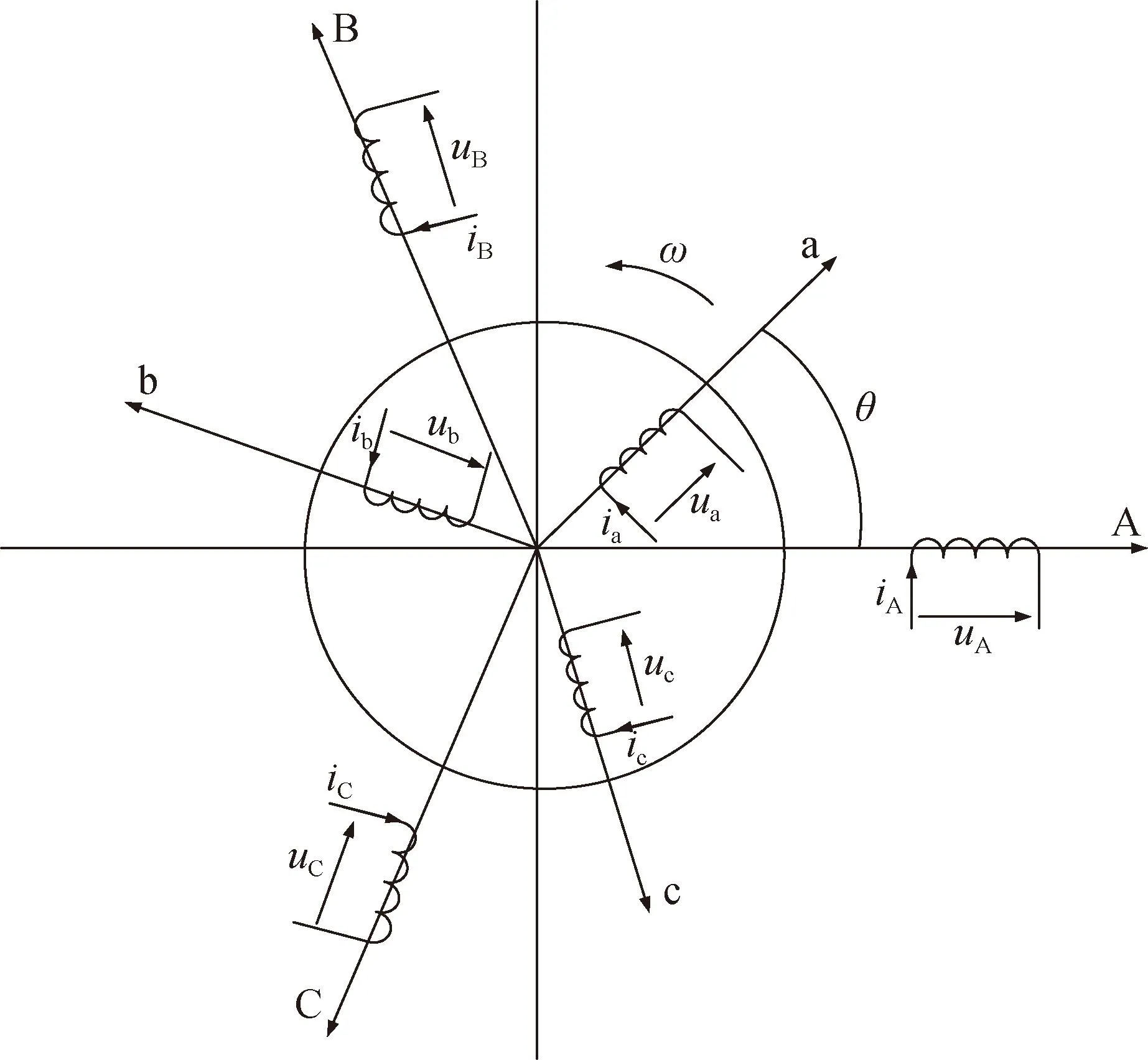
图1 三相异步风力发电机物理模型

通过Clark和Park变换将DFIG的三相静止模型转换至两相旋转坐标dq下,简化为直流形式[26]。

磁链方程为:

(1)

式中:ψsd、ψsq分别为定子磁链的d、q轴分量;ψrd、ψrq分别为转子磁链的d、q轴分量;isd、isq分别为定子电流d、q分量;ird、irq分别为转子电流d、q分量;Lr、Ls分别为转子、定子绕组自感;Lm为定转子绕组互感。其中Lr=Lm+Lrl、Ls=Lm+Lsl,Lrl和Lsl分别为转子、定子漏感。

功率方程为:

(2)

式中:Ps、Qs分别为定子侧输出有功、无功功率;Pr、Qr分别为转子侧输出有功、无功功率;usd、usq分别为定子电压的d、q轴分量;urd、urq分别为转子电压的d、q轴分量。

1.2 转子侧数学模型

在忽略定子电阻Rs时,DFIG的有功无功功率可以近似解耦。本文RSC采用定子电压定向矢量控制,分别通过转子电流的d、q轴分量来控制输出有功功率和无功功率。

对DFIG的有功功率进行控制来满足风电场跟踪最大风能的运行要求;对其无功功率进行控制以实现可控的功率因数来柔性并网。

当RSC通过定子电压定向矢量控制时,转子侧闭环控制器可以表示为[27]:

(3)

式中:Us为定子电压矢量的幅值;Rr、Lr分别为转子的电阻、电感;ωs=ω1-ωr为转差电角速度,其中ω1为电网电压角速度,ωr为转子空间角速度;σ为漏磁系数。

1.3 SSCI机理

DFIG的次同步控制相互作用是由风电机组控制器与线路串补电容耦合引起。SSCI机理示意如图2所示。与传统次同步振荡不同,SSCI与发电机轴系无关[28],且发散速度更快。其次同步振荡频率与输电线路的串补度、并网风机台数、变流器控制参数(主要为RSC内环增益)有关[29-31],因此对控制策略要求更严格。

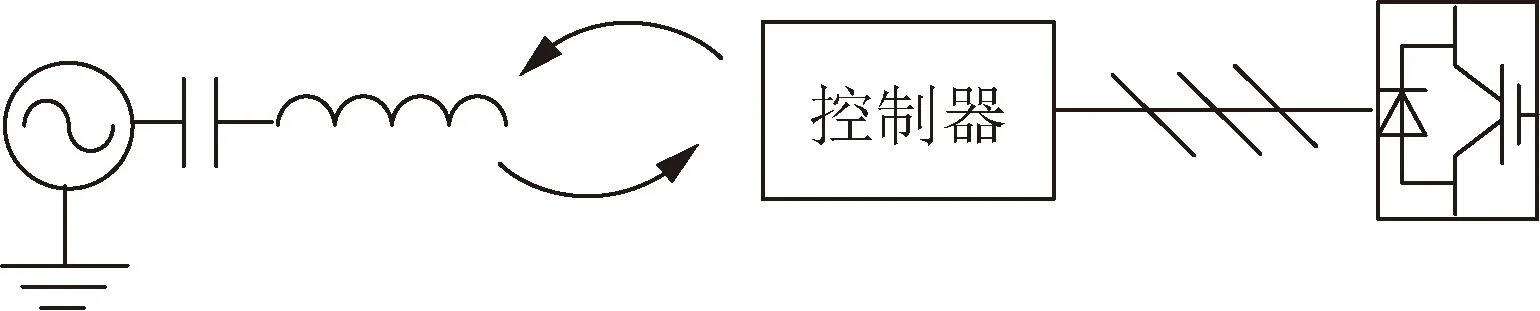
图2 SSCI产生原理框图

双馈风电场SSCI机理如下:在投入串补的输电线路发生小扰动时,转子绕组通过电磁耦合感应到串补线路中的次同步电流分量,便在转子绕组上也出现次同步谐振电流,而RSC在畸变的反馈值作用下通过内环控制输出一个转子次同步电压,进而产生新次同步电流分量,此谐振电流与原次同步扰动叠加,最终使风电机组输出功率呈现振荡发散。

DFIG的自然谐振频率ωer可以表示为:

(4)

式中:XC、XL分别为系统的容抗、感抗;XDFIG为DFIG的等效电抗。同时定义输电线路的串补度K为:

K=XC/XL

(5)

2 基于线性ADRC的抑制策略

对于振荡频率时变SSCI,使用线性ADRC跟踪估计实时系统的总扰动来对SSCI量补偿进而阻断风机控制器与串补之间的耦合作用。此策略无需额外的装置,且利用带宽概念确定的控制器参数鲁棒性较强,整定简单,适用于实际工程。

RSC相对于GSC可以独立解耦控制,本文采用线性ADRC替换RSC传统双环PI的有功内环环节。实际应用中,线性ADRC为了对系统的扰动及噪声进行补偿,选取比控制系统高一阶,故构造3阶线性扩张状态观测器(linear ESO,LESO)和比例与2阶微分反馈控制律,实时补偿次同步扰动量。其中n阶系统线性ADRC的结构框图如图3所示。

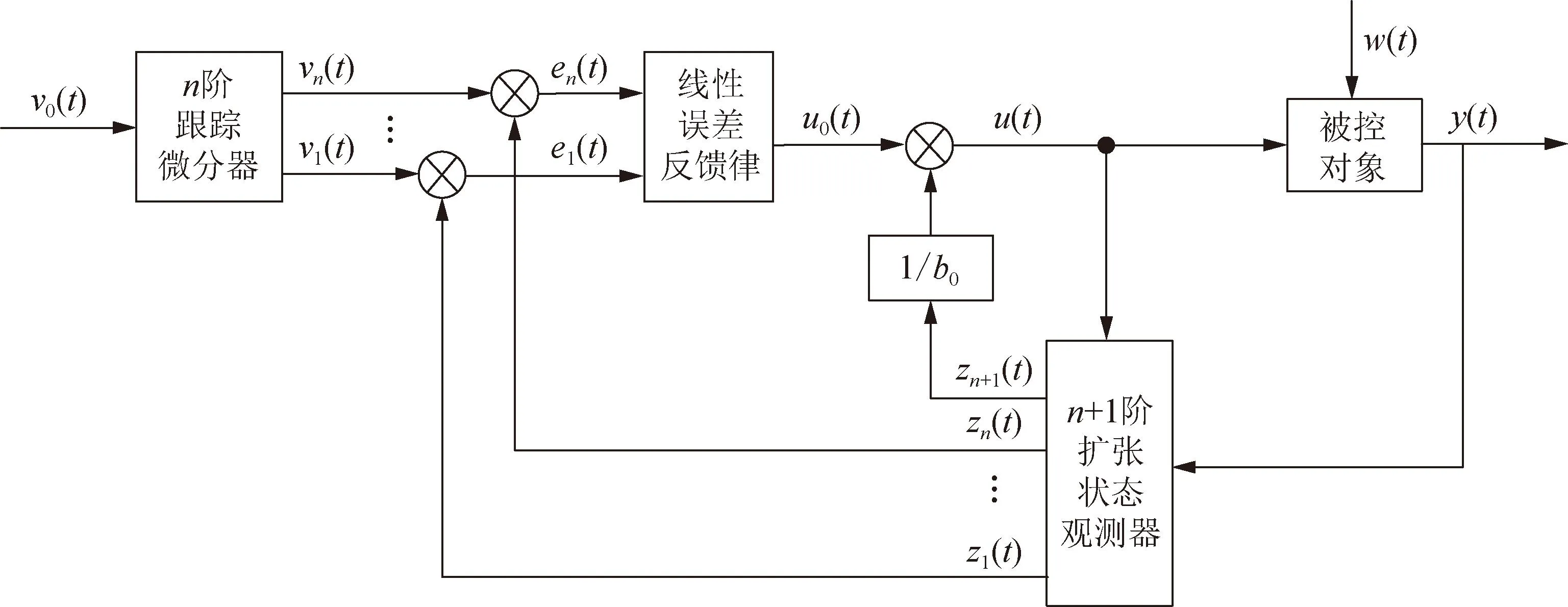
图3 n阶线性ADRC结构框图

2.1 跟踪微分器设计

跟踪微分器的作用是提供2个信号:目标点的过渡信号和其微分信号。过渡信号可以理解为惯性环节,缓慢地向目标点生成一条曲线,向目标点靠近而不阶跃,不超调。

本文使用线性跟踪微分器(linear TD,LTD)来解决“快速性”与“超调”的矛盾。LTD的原理可根据2阶系统的闭环传递函数得到:

(6)

式中:ξ为阻尼比;ωn为无阻尼自然振荡角频率。

当ξ=1时,系统处于临界阻尼状态,会是较为理想的TD。此时可以通过调节参数ωn来调节系统的收敛速度,以更快达到设定值。

由式(6)可以得到对2阶系统LTD的微分方程为:

(7)

令ytd=x1td,utd=vtd,其中x1td为TD的当前状态,vtd为目标状态。则有:

(8)

式中:x1td为过渡曲线,一直跟踪输出vtd;x2td为过渡曲线的微分。

2.2 扩张状态观测器设计

根据式(3)中对于控制输出有功的转子电流d轴方程,等式两边求导升阶,化为:

(9)

整理可得:

(10)

将式(10)中影响被控输出的耦合项和不确定因素用f表示,得到2阶控制对象:

(11)

系统的状态空间可以表示为:

(12)

式中:x=[x1,x2,x3]T为系统的状态向量;x3为总扰动f,并令其导为h(x,w);w为系统的外部扰动;urd为线性ADRC输出给转子侧的控制输入信号;ird为系统输出,也为LESO的输入,控制使其快速跟踪给定参考值irdref。若将新变量也引入到状态变量中,那么可以构成高一阶的状态观测器。

由线性系统式(12)设计线性扩张状态观测器,以实时估计与在线补偿DFIG系统的总扰动:

(13)

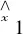
(14)

根据双馈风机系统式(11),n取2。为了确保系统稳定又可以提供良好过渡过程,可以将3阶LESO的特征方程配置为如下形式:

(15)

可以看出观测器n+1个增益系数l简化为观测器的带宽ω0这一个系数,而且通常ω0有较好的鲁棒性和适应性,较大的适应范围使其调试方便。

2.3 扰动估计补偿

根据LESO对系统内外部总扰动的估计,利用扰动反馈量动态补偿次同步扰动量,形成最终的控制量urd来抑制双馈风机SSCI。

LESO可实时观测出系统总扰动时有:

(16)

将最终系统的控制量urd设计为:

(17)

式中:u0为虚拟控制量;b0取为式(11)中控制器增益真值。

2.4 状态误差反馈设计

恰当的线性状态误差反馈可以提高系统抗扰能力,增加稳定性。将式(17)代入式(11)的2阶状态方程中,在b0≈b条件下化为如下新串联积分型系统:

y(2)(t)=bu0(t)

(18)

新系统式(18)中电压虚拟控制量u0基于如下比例与高阶微分反馈控制律:

(19)

式中:k1,…,kn为控制器增益参数。且有:

(20)

2.5 非线性ADRC设计

构建非线性ADRC控制器与本文方法对比[33],其中线性ADRC中的LESO替换为式(21)、(22)中非线性ESO:

(21)

式中:h为积分步长;β01和β02为可调的观测器增益系数;b1为非线性状态观测器补偿因子;z1为跟踪输出y的状态估计量;z2为系统总和扰动的估计量;fal(e,α,δ)为非线性幂次函数。

(22)

式中:α为幂参数,可取为0.5;δ为线性段区间的长度可取其为采样步长;sgn(e)为符号函数。

使用最速反馈函数fhan构建如下非线性状态误差反馈:

(23)

式中:e1为误差;c为阻尼因子;r为速度因子;h1为滤波因子。

fhan函数可以表示为:

(24)

式中:d、d0为fhan函数线性段范围调整参数;y、a、a0为fhan函数内部变量。

2.6 2种ADRC设计对比

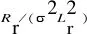
综上所述,基于线性ADRC的SSCI抑制策略系统结构框图如图4所示。

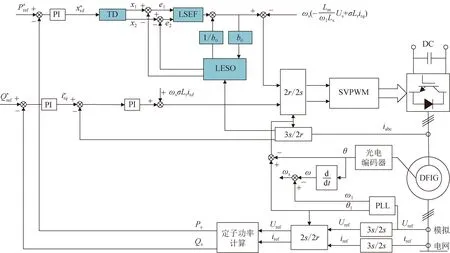
图4 基于线性ADRC的SSCI抑制策略系统结构框图

2.7 双馈风机的线性ADRC控制结构

在RSC通过定子电压定向矢量控制时,根据式(3)转子侧闭环控制器可知,通过控制转子电压的d、q轴分量来调节转子电流d、q分量ird、irq进而稳定DFIG的输出功率。因此本文的双馈风机线性ADRC控制原理可以概括为:转子侧外环比较风机输出有功无功的参考值与实际值之后通过PI控制输出一个转子电流的d、q参考作为内环输入,再分别通过控制转子电压d、q轴分量,实现双馈风机有功和无功功率的解耦控制。其中图4蓝色部分为替代传统PI内环的线性ADRC控制,TD对转子电流d轴分量ird安排过渡过程,避免启动时系统输出超调过大,并且获得其微分信号,将目标误差与微分误差输入LESO;LESO作为ADRC的核心,根据输入、输出数据来观测系统的各个状态总扰动;LSEF通过设计的比例与高阶微分反馈控制律有效抑制扰动,增强系统的稳定性;最后由式(17)对反馈控制量安排补偿过程,使次同步扰动量被动态补偿,抑制SSCI,并形成最终的控制量urd。

3 仿真分析

为验证线性ADRC在不影响DFIG稳态和暂态控制性能的基础上对SSCI的抑制能力,本文在Matlab/Simulink平台上搭建了图5所示的DFIG经串补线路输送功率的等值模型。图5中,100台额定容量为1.5 MW、额定电压为0.69 kV的风机经过两级升压,最后经默认串补度为40%的线路并入220 kV远距离输电。采用单台风机等值整个风电场会引入一定误差,但是风电场参数变化对次同步振荡的影响规律与多台风机等值是一致的;所以双馈风电场多台连接同一母线的相同型号风机在相同工况下运行可以等价为一个大容量单机模型[34]。DFIG、变压器及串补线路的参数如表1所示。

表1 DFIG及线路参数

图5 DFIG经串补线路输电等效模型

3.1 线性ADRC的稳态、不平衡运行性能

3.1.1 稳态运行

先与PI控制比较,来验证线性ADRC不影响DFIG的稳态运行能力。在不投入线路串补电容的情况下进行仿真,设置风电场风速在1 s时由初始7 m/s突变为9 m/s,线性ADRC控制下风机输出有功与传统双环PI对比,如图6所示。

图6 风速变化风机输出有功功率响应

由图6可见,随风速的增加,DFIG输出的有功功率跟踪风速而增加并快速达到新稳态。与PI控制相比,ADRC超调量更小,这是因为PI控制在初始状态时,直接采取误差反馈来消除误差,使初始控制量太大而出现超调的现象;本文线性ADRC中2阶跟踪微分器通过过渡曲线及其微分加入惯性和阻尼来解决超调量和快速性的矛盾。若追求更快的调节速度,可以选择使用2阶非线性跟踪微分器。因此,转子侧内环采用线性ADRC在DFIG稳态运行时具有良好的控制能力。

3.1.2 不平衡电网下运行能力

风力发电必须保证风机在电网故障引起的电压下降期间保持在线。在风速9 m/s且不投入线路串补电容的情况下进行仿真;引入不平衡电压,工况设置a相电压发生10%的不平衡跌落。在此工况下,验证线性ADRC策略下风机的平稳运行能力。图7给出了不平衡跌落下功率相应曲线。

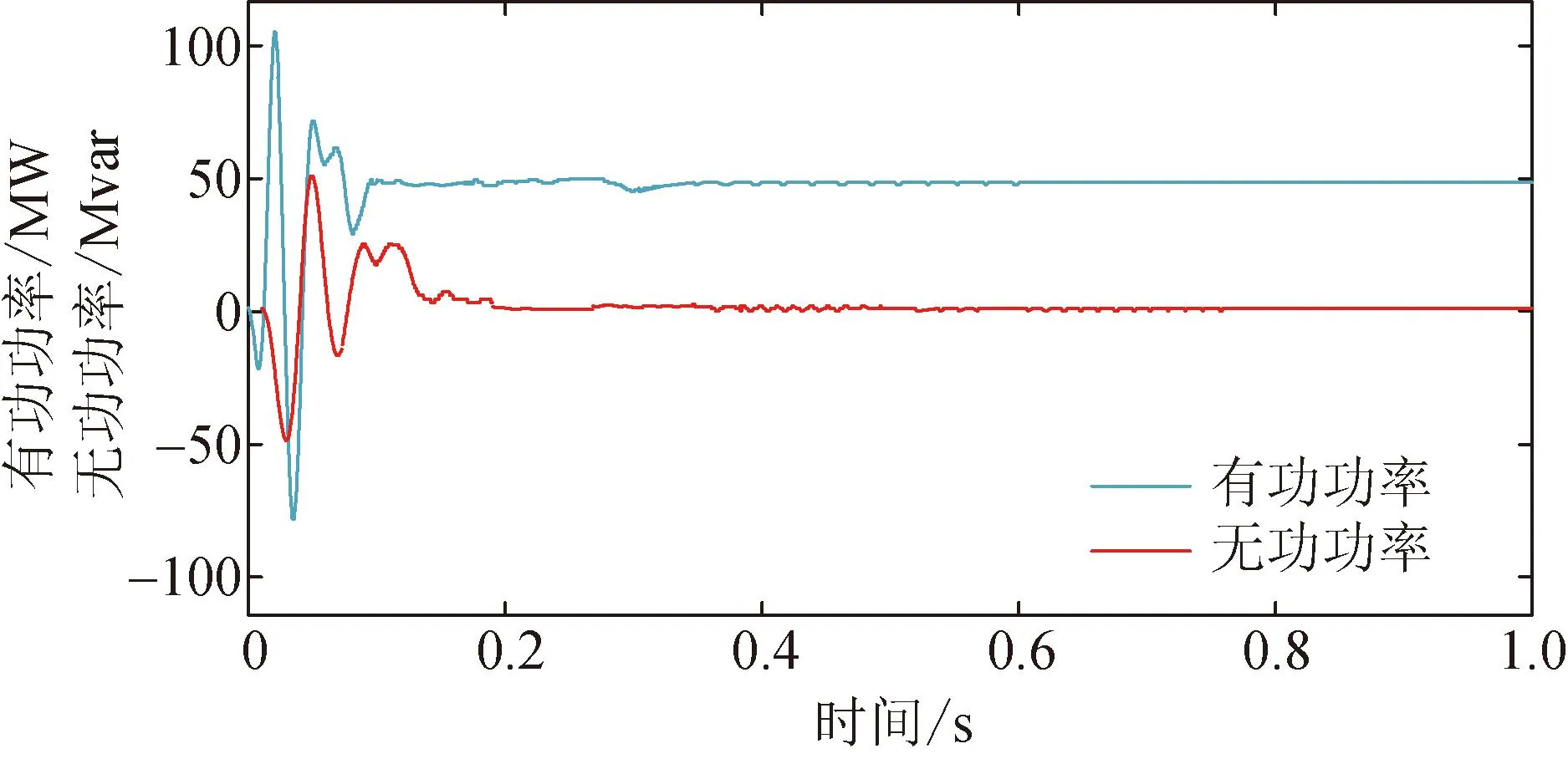
图7 不平衡电网电压下输出功率

由图7可见,不平衡电网电压下线性ADRC控制策略可以使风机输出有功功率和无功功率快速平滑过渡到给定值,减小电网电压不平衡对DFIG运行所造成的扰动。在风电场其他扰动下,线性ADRC也可以稳定运行。因此该策略不影响系统运行性能。

3.2 线性ADRC的SSCI抑制能力

3.2.1 与PI的运行性能对比

投入线路串补装置来检验线性ADRC对SSCI实时估计和反馈补偿的有效性。根据不同控制策略的输出功率响应来对比系统抗扰运行能力。

当风电场风速稳定在9 m/s,风机并网台数为100台时,初始串补度为10%,在传统双环PI策略下整定参数,系统稳定运行输出功率恒定后,在0.5 s时系统提高线路串补度为40%,在1.4 s时RSC内环调整为线性ADRC,仿真结果如图8、9所示。其中:图8为双环PI控制与线性ADRC控制策略对SSCI的抑制性能对比;图9为线性ADRC投入时输电线路电流变化图。

图8 PI与线性ADRC策略的SSCI抑制性能

图9 线路的a相电流

由图8、9可见,系统SSCI的稳定性与线路串补度成反比。在较小串补度情况下,即使维持传统PI控制,整个DFIG远距离输电系统对于次同步分量可以保持正阻尼而维持正常运行;而随着串补度提升,在不采取额外针对抑制措施时,风机输出有功功率将叠加发散,同时线路出现对应的次同步电流分量,此时系统对次同步分量呈现整体负阻尼特性。1.4 s投入线性ADRC,对SSCI实现快速有效抑制,消除了电流中次同步分量,稳定了风机输出功率,即验证了其能实时估计SSCI谐振分量,通过补偿来消除RSC控制器与串补之间感应叠加作用。

3.2.2 串补度改变时与SSDC的运行性能对比

双馈风力发电机向电网输送功率时一大特性就是时变性,其运行工况并不是稳定在某一串补度,由式(4)可知,输电线路串补电容变化时,双馈风机自然谐振频率fer也会相应变化,其中次同步功率振荡频率表现为f1-fer,本文搭建系统中f1为50 Hz。随线路串补度上升,系统自然振荡频率上升,有功振荡频率下降,同时振荡幅值与发散速度增加。

在实际工程中常在双馈风机的变流器中附加次同步阻尼控制器来应对SSCI风险,其中根据SSDC的输入控制信号不同分为常见的3种[35]:一是线路补偿电容电压有效值VC作输入控制信号并输出到GSC中;二是转子转速作为输入信号,对2阶带通滤波器提取的次同步分量幅值相位补偿后嵌入RSC的d轴和q轴的输出电压回路中;三是将转子电流的d、q轴分量ird和irq作为输入控制信号,通过2阶带通滤波器选出其中次同步分量,再通过PI对其幅值相位补偿后输出嵌入RSC中。

第3种SSDC的故障抑制能力更强同时输入信号采集相对简单[35],故而仿真将转子电流为输入量的SSDC(为行文方便,后文SSDC皆指此种)与线性ADRC在控制性能和参数鲁棒性的维度进行对比。

考虑SSCI一般发生于风电场输出功率较小工况,故设定风电场风速稳定在9 m/s;风机并网台数为100台,线路串补度默认初始为40%,在此运行工况下整定SSDC参数,使SSDC达到最佳SSCI抑制效果。SSDC与线性ADRC在1 s前控制均达到稳定运行状态。此时在1.2 s改变220 kV线路串补度,以比较不同控制方法对变化工况的鲁棒性。

当1.2 s时串补度提升到50%时,输出有功功率响应特性如图10所示。由图10可见,输电线路串补度为50%时,采取SSDC和线性ADRC均能抑制SSCI,其中SSDC需要0.5 s才能基本抑制次同步分量,振荡抑制缓慢,阻尼效果欠佳;而线性ADRC调节时间为0.2 s,可以快速稳定输出有功。

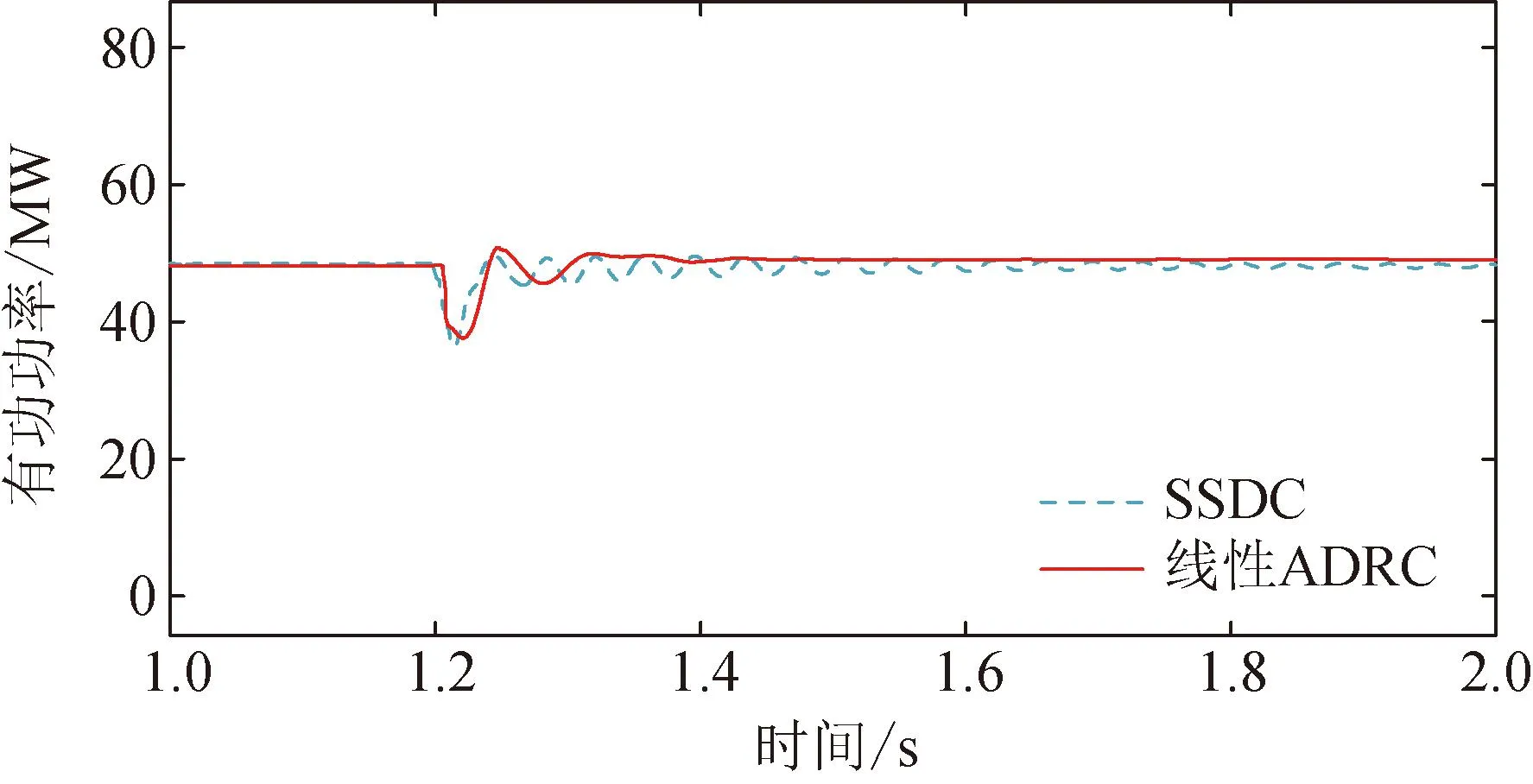
图10 50%串补度输出功率响应对比

当1.2 s时串补度提升到60%时,输出有功功率响应特性如图11所示。由图11可见,输电线路串补度60%时,次同步工况变化(次同步频率、幅值),之前整定的SSDC参数已经不再适用,SSDC策略下的风机系统阻尼减小,系统开始振荡,体现为输出功率波形产生次同步畸变。而线性ADRC在参数不变的情况下对该串补度次同步分量依然有良好的抑制。

图11 60%串补度输出功率响应对比

考虑严重SSCI发生工况,当1.2 s时串补度提升到80%时,输出有功功率响应特性如图12所示。

图12 80%串补度输出功率响应对比

串补度增加到80%时,谐振频率变为33.3 Hz。振荡频率与40%串补度时发生较大偏移,原SSDC不足以抑制SSCI现象,风机输出有功强烈振荡发散。在改变串补度工况下,220 kV线路参数设置及相应振荡频率特性见表2。由表2可知,线性ADRC对振荡频率变化具有良好的抗干扰能力,串补度不同的各种工况下均能保证良好的次同步抑制能力。

表2 不同串补度下有功振荡频率

3.2.3 风速改变时与SSDC的运行性能对比

3.2.1节自然谐振频率的改变对SSDC的控制效果有较大影响。故而本节控制考虑振荡频率偏移不大的工况,在3种不同风速下对比SSDC与线性ADRC策略。

本节线路串补度固定接入为40%,在初始电风速稳定在9 m/s的工况下整定SSDC参数,使之达到最佳SSCI抑制效果。SSDC与线性ADRC在1 s前控制均达到稳定运行状态。在1.2 s依次降低风速来比较2种控制方法对风速变化的鲁棒性。

当1.2 s时风速降低为8 m/s时,输出有功功率响应特性如图13所示。

图13 风速8 m/s时输出功率响应对比

由图13可见,风速由9 m/s降低到8 m/s时,SSDC与线性ADRC均能对SSCI取得有效抑制效果,使风机转到一个输出功率减少的新稳态,而线性ADRC调节时间更短,超调量更小。

当1.2 s时风速降低为7 m/s时,输出有功功率响应特性如图14所示。

图14 风速7 m/s时输出功率响应对比

由图14可见,风速由9 m/s降低到7 m/s时,随着风速的减小,风电场输出功率减小。此时SSDC无法达到最优抑制效果,对振荡抑制缓慢,且相对稳定后输出有功振荡的幅值增大;而线性ADRC无需重新整定参数,依旧能对SSCI取得良好抑制效果。

当1.2 s时风速降低为6 m/s时,输出有功功率响应特性如图15所示。SSDC此时系统阻尼过小,系统功率振荡发散,SSDC必须重新整定参数。而线性ADRC无需改变参数,依然对不同风速下的SSCI能有效抑制,保证风机系统稳定运行。在改变风速工况下,220 kV线路参数设置及相应振荡频率特性见表3。

表3 不同风速下有功振荡频率

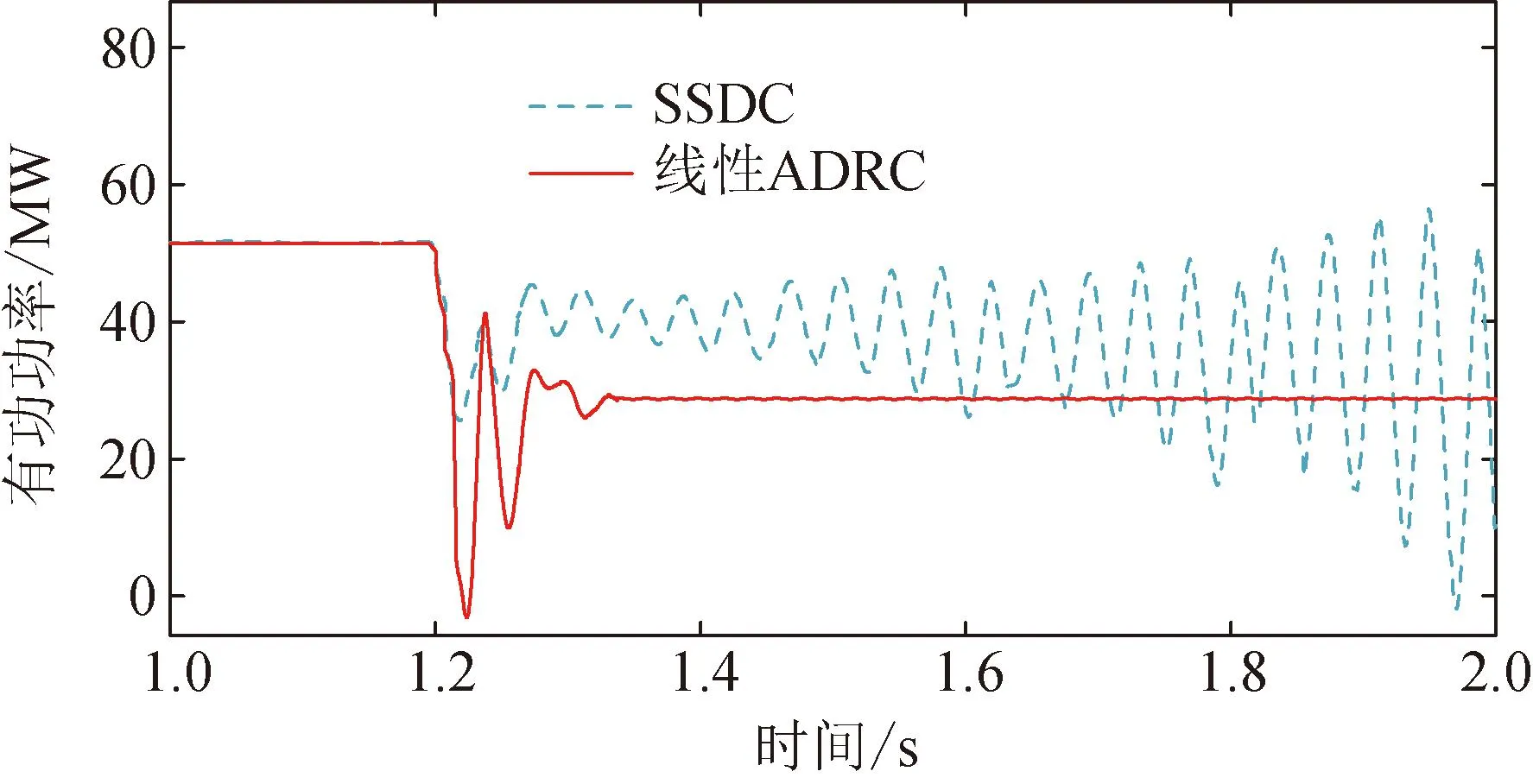
图15 风速6 m/s时输出功率响应对比

3.2.4 与非线性ADRC的运行性能对比

考虑对控制器抑制能力要求最高的工况,设定风电场运行风速为9 m/s,串补度40%,稳定后在1.2 s切换为低风速6 m/s,线路串补度80%,在此运行工况下对比非线性ADRC与线性ADRC的运行性能。其中非线性ADRC策略中幂参数α取0.5;δ取采样步长h;控制器增益β01和β02分别取h、h/6。仿真结果如图16所示。

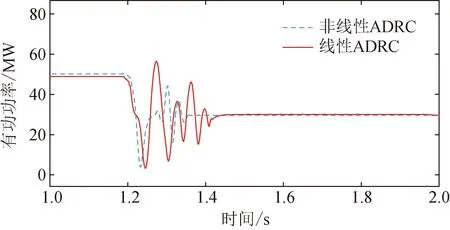
图16 线性ADRC与非线性ADRC输出功率响应对比

由图16可见,2种ADRC均能在较短时间内在恶劣工况下有效抑制SSCI。线性ADRC的输出功率曲线超调量和调节时间略大于非线性ADRC,这是由于非线性扩张状态观测器和误差反馈组合控制器这2个主要环节是以非线性函数形式呈现的,而这2个部分对误差的实时估计反馈更加精准;考虑实际工程非线性ADRC理论分析困难、整定参数较多且计算复杂,往往不能达到最优控制状态,此控制速度精度优势会被抵消。而与其相比,线性ADRC在拥有相近稳定控制能力的情况下极大简化控制器模型,使参数整定过程简化。

4 实验验证

为了验证本文设计的基于线性ADRC的次同步抑制策略的动态性能和鲁棒性,通过图17所示RT-LAB半物理平台进行实验。

图17 基于RT-LAB的DFIG半物理实验平台

图17中,RT-LAB实验平台上实时运行的仿真模型已经由第3节Matlab/Simulink建立,其中含有双馈风力发电机、网侧变换器和转子侧变换器及含串联补偿电容的输电线路等,在进行转子侧单独实验时,背靠背变换器中直流母线等效为一个恒定直流电压源。而dSPACE部分对实际受控信号进行数据采样,根据各变换器的控制和调制策略输出控制序列。dSPACE实时系统拥有实时性强、可靠性高、扩充性好等优点。其中dSPACE原理为:DS1103是一种适用于逆变器控制的控制器板,可实现硬件与Matlab/Simulink仿真环境之间的连接,实现算法、编译算法并转换成C语言代码,然后加载到实时dSPACE处理器上;DS1103ADC和DS1103DAC模块负责对风机并网电压、电网电流等实际系统连续的模拟量和时间、幅值离散的数字量之间进行转换;再由DS1103SLDSP生成脉冲宽度调制(pulse width modulation,PWM)信号以实现调制。RT-LAB驱动系统将DFIG并网模型加载到所需的I/O接口的实时仿真平台上。

首先验证搭建模型和实验方法的正确性,在3.1.1节不投入串补电容的稳态工况下进行实验。比较本文线性ADRC策略下风机的启动与风速变化功率追踪效果,结果如图18所示。

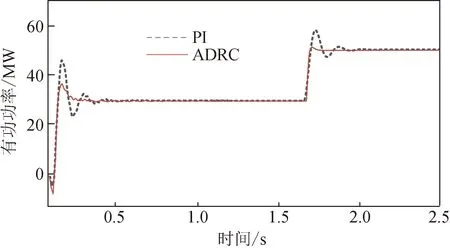
图18 风速变化输出功率对比

由图18可见,线性ADRC控制策略可以达到预期目标,且对比PI而言超调量更小、更快稳定到目标功率。

考虑串补度变化的工况进行实验,在3.2.2节系统参数的情况下,设定默认风速为9 m/s,线路串补度10%,等系统运行稳定后在1.2 s时串补度突变为60%,引起23.7 Hz的次同步振荡问题。PI、SSDC与线性ADRC的控制效果对比如图19所示。

图19 串补度变化时输出功率对比

由图19可见,在线路投入高串补时PI控制输出有功迅速振荡发散,即导致了60%串补度下的次同步振荡。SSDC与线性ADRC均可在一定程度上抑制该变化的次同步工况,但是SSDC已无法达到最优抑制效果,对振荡的抑制较慢;而线性ADRC的抑制效果没有受到影响。

最后验证3.2.3节风速变化线性ADRC策略下输出功率响应,接入40%线路串补度,待系统稳定后,依次将风速由9 m/s降低为8、7、6 m/s。其实验结果如图20所示。

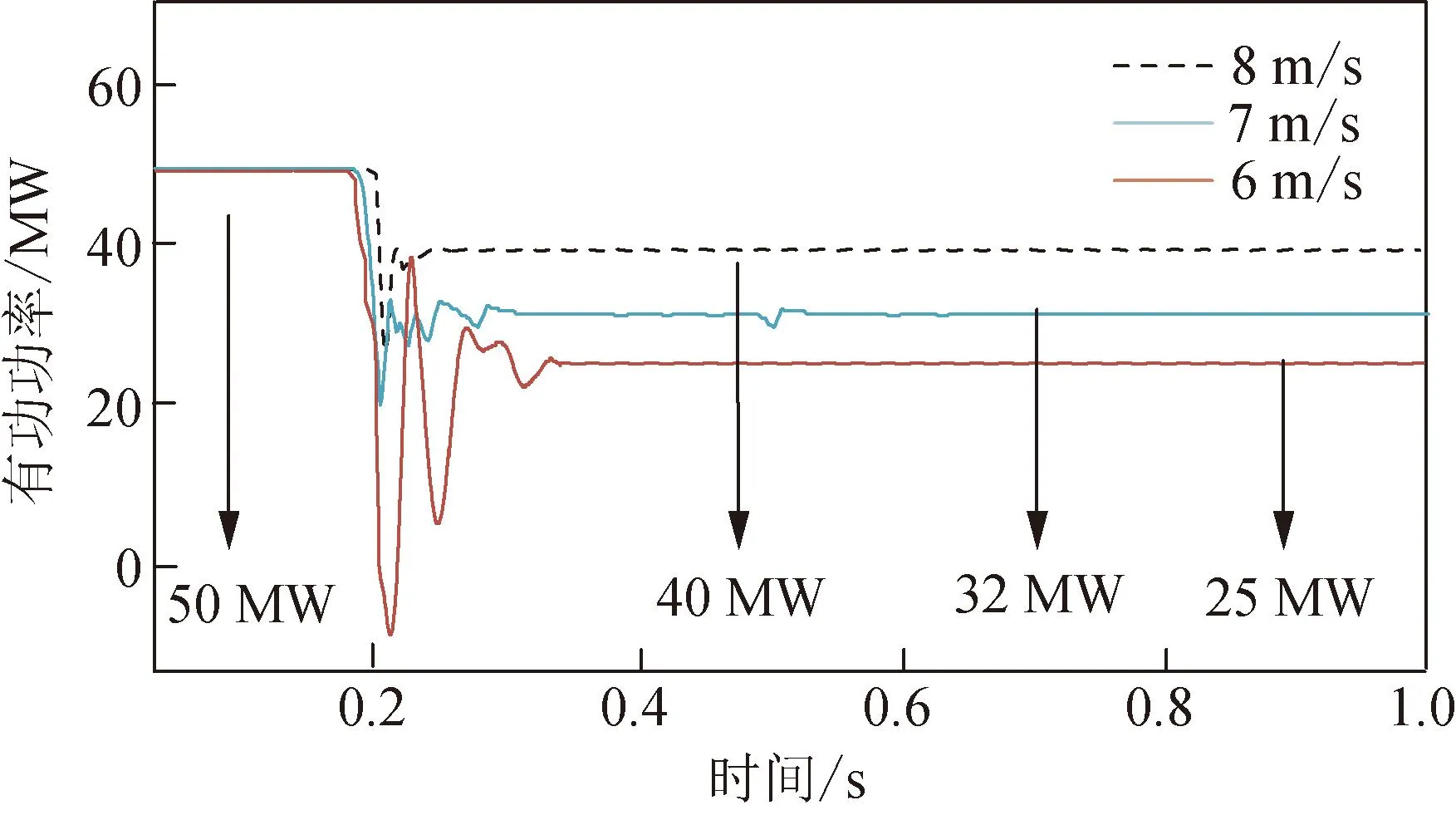
图20 降低风速时输出功率响应

由图20可见,线性ADRC对不同风速下SSDC均能有效抑制,增强了系统鲁棒性;风速突变下输出功率能迅速过渡到新稳态,增强了系统稳定性。

综上,本节RT-LAB实验平台上半物理仿真实验结果与第3节的基于Simulink软件仿真结果完全一致,也即DFIG转子侧线性ADRC策略对工况时变的次同步抑制有着良好性能。

5 结 论

本文针对DFIG串补线路的次同步控制相互作用问题,提出了一种基于线性自抗扰控制的双馈风力发电机转子侧换流器抑制策略,通过阻断串补线路次同步分量和RSC控制器的相互作用来实现多运行工况下的SSCI抑制。并基于实际工程模型,在Matlab/Simulink和RT-LAB实验平台上验证了该抑制策略的有效性,所得结论如下:

1)稳态和不平衡电网电压下,线性ADRC有良好运行特性,即不影响DFIG暂态稳态运行能力。

2)对于变化振荡频率的SSCI问题,线性ADRC相比附加次同步阻尼控制策略,对系统参数变化的抗干扰能力更强,不同工况下都有很好的适应性。

3)不同于非线性ADRC,线性ADRC的参数整定简单,大范围内都有良好抑制效果,具有较强的鲁棒性。