一种基于修正电压的新型暂态量保护原理

薛士敏,李翔宇,陈文杰,张君婷,张皓明,阴文湘

(天津大学电气自动化与信息工程学院,天津市 300072)

0 引 言

基于模块化多电平换流器(modular multilevel converter,MMC)的柔性直流输电技术在电能质量、功率控制、供电可靠性等方面具有明显优势,成为构建新型电力系统的重要技术之一,同时也为高电压等级、大容量的柔性直流输电系统的发展奠定了基础,具有广泛的应用前景[1-8]。然而,如果直流线路发生故障,由于柔性直流输电系统的弱阻尼、低惯性的特性,故障电流上升速度快,幅值大,所以通常要求保护在极短时间内识别故障,以免引起不必要的停运及扩大停电范围[9-10]。因此,研究能够快速识别故障的线路保护对于柔性直流系统来说十分必要。

柔性直流系统线路保护可分为单端量保护和双端量保护。单端量保护依据选取的故障信息类型,可分为频域单端量保护和时域单端量保护。频域单端量保护通过提取电气量的频域特征进行故障识别,一般存在原理复杂、计算量大、保护整定值难以选择等问题[11-14]。时域单端量保护具有方法简单、动作速度快的优点,可满足柔性直流系统对保护速动性的严苛要求[15],具有较好的应用前景。

时域单端量保护主要通过检测电压、电流突变量等数值特征或故障行波的波形特征来构成故障识别判据[16-23],现有直流工程以行波保护和微分欠压保护作为主保护,存在耐过渡电阻能力较差的问题,无法满足柔性直流系统对保护灵敏性的要求[24-25]。针对直流线路行波保护灵敏性较差的问题,文献[20-23]分别提取表征故障首行波波头陡度的波形特征,由于过渡电阻对波形的变化影响较小,所以具有较好的耐受过渡电阻能力,但雷击干扰下,可能发生误动。文献[26]利用故障电压幅值判据与极值时间判据相配合构造行波保护方法,但整定值裕度较低,部分故障情况下可能误动。文献[27]构造了不同采样周期下的时域暂态电压比判据,文献[28]基于电压反射行波二阶差分构造保护方案,两者都削弱了高阻对保护的影响,但时间窗均超过了3 ms[29]。文献[30]综合低压判据、电压变化率判据和方向性过流判据识别故障,但仍然存在耐过渡电阻能力差的问题。文献[31]提出一种基于电流量的幅值及变化率的保护原理,可靠性好,但耐受过渡电阻的能力较差,且不能实现故障的选极。总之,单端量保护的综合性能还尚未完全达到柔性直流系统的要求。

相较于单端量保护,双端量保护具有可靠性高、耐过渡电阻能力较强等优点[32-38],但受限于通信传输速率与通信距离,只能在有限的传输距离内满足速动性要求,所以通常作为后备保护使用。其中,方向纵联保护仅需传递具有方向标识的逻辑量,通信压力较小且通信方式相对灵活[24]。

针对传统单端量保护在柔性直流系统中的不足,本文提出一种基于修正电压的新型暂态量保护原理。首先分析故障后柔性直流系统的暂态过程,通过解析区内、外故障下直流线路的暂态特征,提出一种电压修正算法,基于修正电压的积聚量有效区分了区内与正向区外故障,并利用新的方向元件构成纵联方向后备保护,解决了单端量保护在高阻故障下灵敏度较低的问题。最后基于PSCAD/EMTDC仿真平台搭建四端柔性直流系统模型并仿真验证所提保护方案的性能。

1 柔性直流输电系统典型拓扑结构

图1为四端柔性直流系统示意图,其中,MMC子模块采用半桥子模块,直流线路的接线方式为对称双极结构。图中:L12—L43表示各线路的限流电抗器,P12—P43表示各线路两端的继电保护装置,Pm为母线侧的保护装置,f1—f10表示不同的故障位置,其中,f1、f2、f3分别位于直流输电线路首端、中点、末端,f8、f9、f10分别位于输电线路距离P143 km、30 km、150 km处,f4、f5分别位于MMC4侧、MMC1侧母线处,f6、f7分别位于Line34、Line12中点。

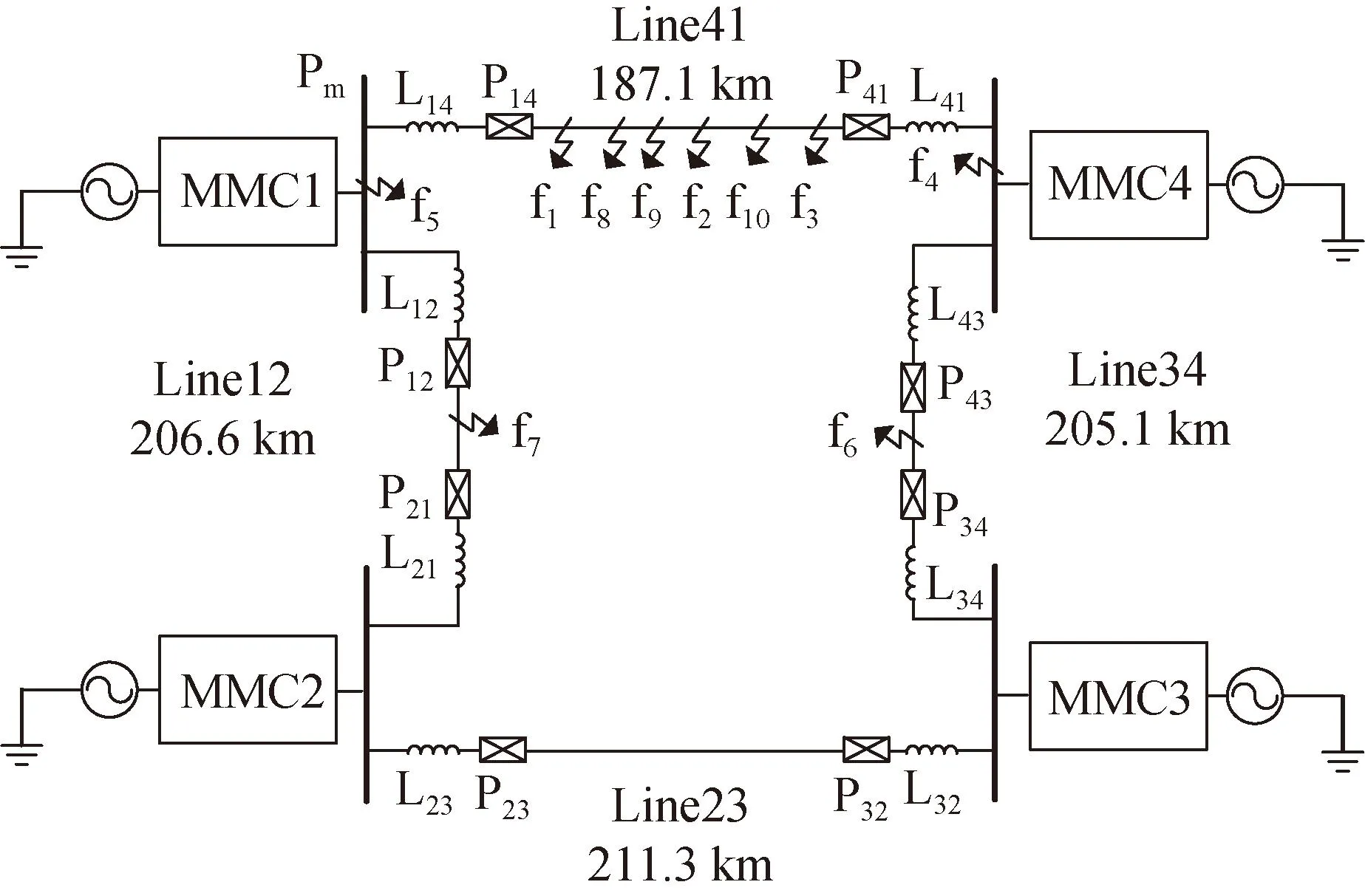
图1 四端柔性直流输电系统

2 故障行波特征分析

由于柔性直流线路中极分量存在耦合,故常采用解耦后的模量进行暂态分析,且与0模波相比,1模行波色散程度小,稳定程度更高,因此本文采用1模行波作为分析对象。常用的解耦公式为:

(1)

式中:Fp、Fn分别是正负极电气量;F1、F0分别表示1模分量、0模分量。

2.1 区内故障分析

线路Line41区内发生正极接地故障时,根据叠加定理,故障后的网络可视为正常网络与故障分量网络的叠加。因为系统的故障特性主要由行波故障分量决定,而故障行波只存在于故障分量网络中,所以仅对故障分量网络进行分析,如图2所示,图中Cm、Lm为MMC等效电容和电感,在未经特殊说明的情况下该图及后续提到的所有电压和电流均默认为故障分量。ΔUdc为故障前线路对地电压,于是故障点1模初始行波表达式如式(2)所示[39]。

(2)

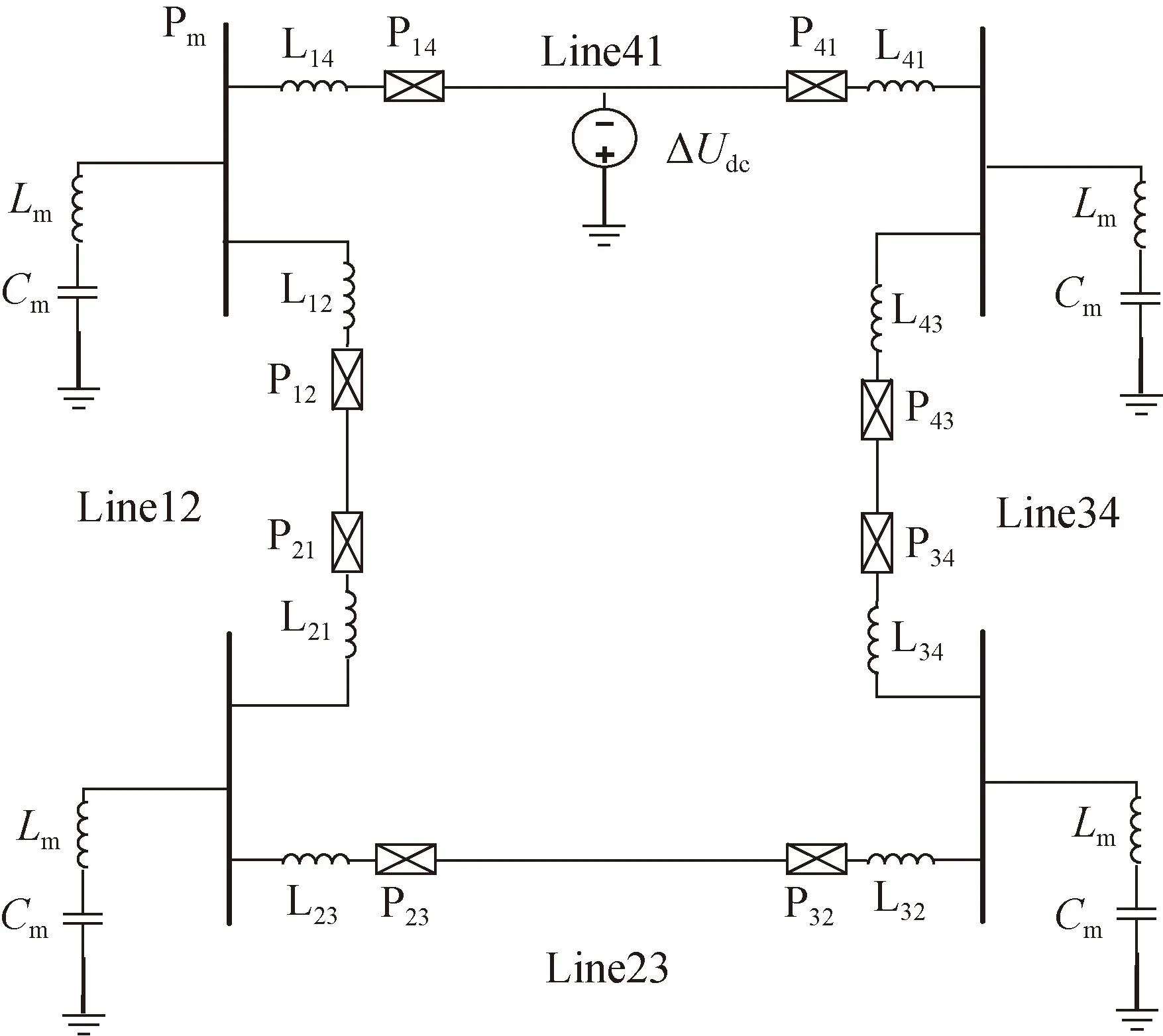
图2 区内故障故障分量网络等值电路

式中:ZC1、ZC0表示故障线路特征阻抗的1、0模分量;Rg为故障点的过渡电阻。

初始行波抵达MMC时将发生折反射,以P14为例,在背侧线路反射波回到MMC1前,初始行波在P14处的1模彼得逊法等效电路,如图3所示。图中所有阻抗和暂态量均为其1模分量,其中,Δu′f为初始行波抵达MMC1边界的入射波,其满足Δu′f=AlΔUf,Al、ΔUf、i14、i12、im、Z41、Z12和L41、L12分别表示线路的衰减系数、故障点处的暂态激励、P14处测量的故障电流、折射到线路Line12和MMC1上的电流、线路Line41和Line12的特征阻抗和限流电感。

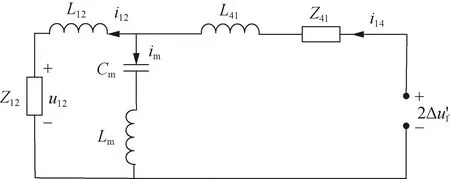
图3 区内故障时初始行波的1模彼得逊等值电路

根据图3列写复频域方程组为:

(3)

式中:ΔU′f、I14、I12、Im分别为图3中Δu′f、i14、i12、im的复频域表达形式;Z∑m=sLm+1/(sCm)。

得到复频域的通解为:

(4)

进一步求得各电压的1模分量为:

(5)

解得P14处电压和电流的1模分量为:

(6)

式中:Z∑1=sL12+Z12;Z∑4=sL41+Z41。

2.2 正向区外故障分析

当图1中MMC4母线f4处发生经过渡电阻Rg的正极接地故障时,初始行波在P14的1模彼得逊等效电路图如图4所示。

图4 区外故障时初始行波的1模彼得逊等值电路

Δu′f的复频域形式如式(7)所示[40]:

(7)

式中:A41(s)为线路对初始行波的衰减系数。

线路Line41发生正向区外和区内短路故障时,P14处的1模彼得逊等值电路基本相同,只有入射波ΔU′f不同,故将式(7)中的入射波ΔU′f代入到式(6)中,即可得到正向区外故障下的电压u14和电流i14的复频域表达式。在上述各表达式中代入相关参数,再利用拉普拉斯反变换,即可得到时域表达式。

图5为区内末端f3处和MMC4母线f4处分别发生正极接地短路故障时,P14处故障电压、电流1模分量的理论计算波形、仿真波形。可见故障初期,仿真波形与理论计算波形变化趋势基本保持一致。由图5可知,由于区外故障时线路两侧边界电感对电压行波产生明显的阻碍作用,极大限制了电压的峰值,同时也减少了电压的变化率,所以区内故障下的电压幅值和变化率明显大于区外故障下的;而在故障初期的1.2 ms内,区内、外故障下的电流幅值和变化率相差不大[10]。总之,在故障发生后的短时间内,边界电感对故障电压影响程度相比于对故障电流的影响程度更大,因此利用电压信号可以更加灵敏地反映故障特征。对图5中的电压、电流1模分量的变化量进行积分,在1.2 ms内,区内故障的电压变化量积分值比区外故障下的多87.03%;区内故障的电流变化量积分值比区外故障下的多42.73%。该结果与上述理论分析基本一致,进一步证实了在边界电抗器装在线路两侧的柔性直流系统中,更适合利用电压判别区内、外故障。

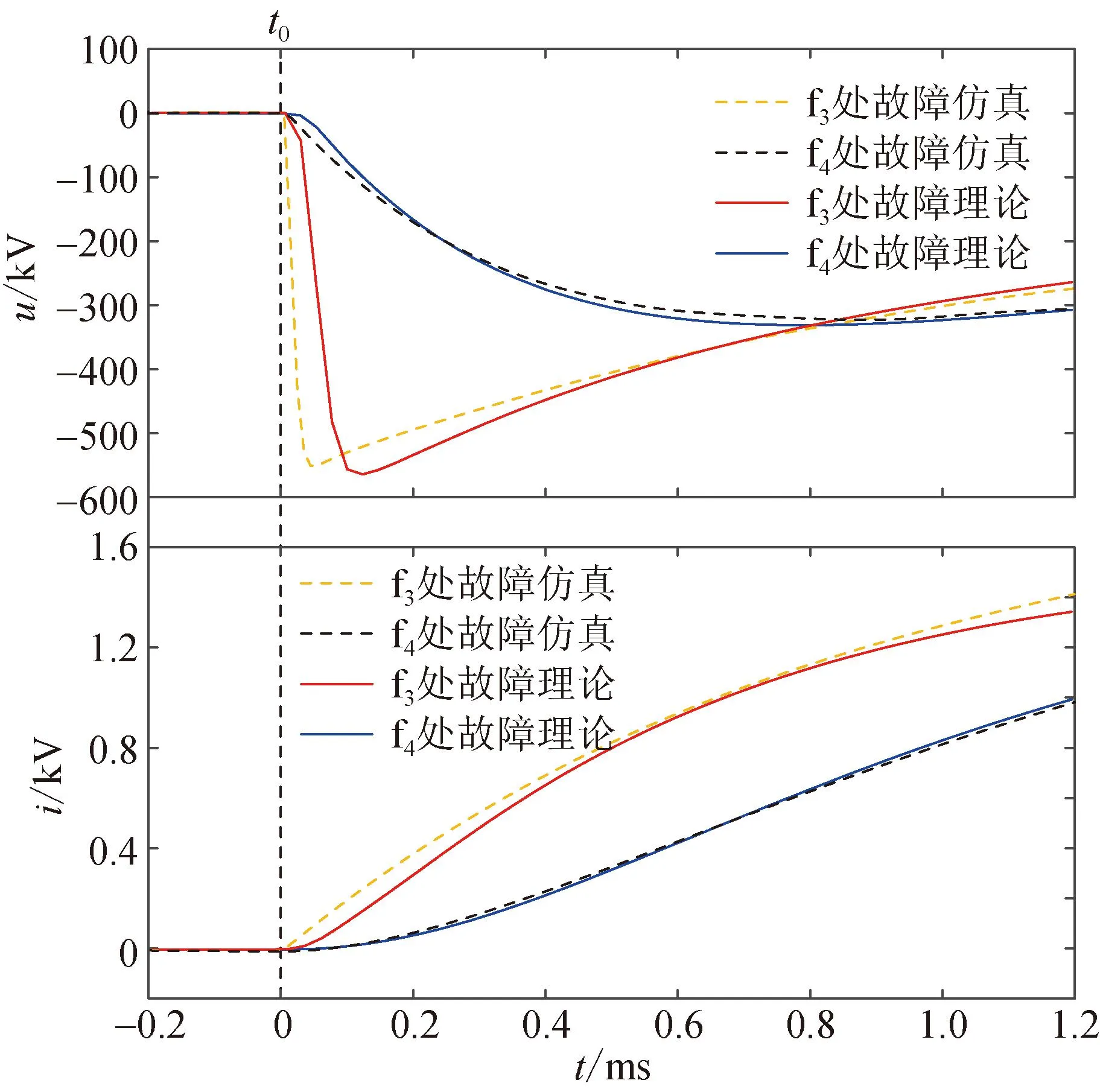
图5 区内、外故障下电压、电流的波形图

3 故障识别方法及判据

3.1 电压修正算法

图6为区内末端f3处和MMC4母线f4处分别发生正极接地短路故障时,P14处故障电压1模分量的仿真波形。其中,a为初始行波抵达P14处电压开始变化的起点,b、b′和c、c′点分别为区内和区外故障下的电压的第一个极值点和二次行波返回导致电压再次突变的起点。分析可得,区内故障时,电压在a—b段急剧下降,并在t1时刻降到极值点;区外故障时,由于边界电抗器的阻碍作用,电压在a—b′段的下降较慢,在t2时刻达到极值点。初始行波运动到MMC1后对限流电抗器和换流器充电,所以从极值点到t3这段时间内电压呈对数规律回升[9],且区内故障的电压变化率大于区外故障。所以在故障初期的t1—t3内,较难从电压幅值的角度区分区内、外故障,而t3后反射波的到来使得区内、外故障下的故障电压变化趋势发生改变,更难从电压幅值的角度进行区分,其实质是由于电压增减变化的双重性和时间上的不确定性造成的。因此,如果假设电压只朝一个方向变化,就可以增大区内、外故障下的电压差异,从而使故障识别和定位变得更容易。

图6 区内、外故障时电压故障分量的仿真波形图

为实现上述假设(本方案假设电压只朝负方向变化),对采集到的电压数据进行修正,当电压变化率为负时,电压遵从原变化趋势,不进行修正;当电压变化率为正时,先将电压变化量取反,然后加在前一时刻电压值上,从而得到当前时刻的修正电压值。具体的处理算法如式(8)所示。

(8)

式中:Δu(i)=u(i+1)-u(i);u(i)为采集的原始电压数据;uxz(i)为修正电压。

图7为区内末端f3处和MMC4出口f4处发生故障时P14处的修正电压波形图。图8为Line41上的不同位置发生正极接地故障的修正电压波形图。区内其他位置与MMC4母线f4处的故障的修正电压具有更大的差距。修正电压综合利用了故障后的电压幅值和电压变化率特征,使得区内、外故障间的差异更明显,因此,利用修正电压的幅值可以更灵敏准确地区分故障。

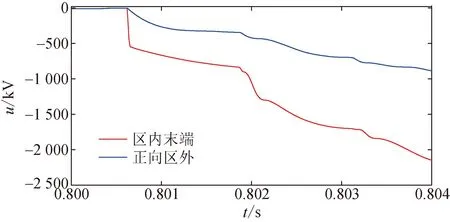
图7 区内、外故障时修正电压的波形对比图

图8 区内不同故障位置与区外修正电压波形图

3.2 启动判据及故障选极判据

正常运行时,直流电压基本不变;故障后,电压波动剧烈。所以,可以以电压幅值和电压变化率的组合判据作为保护的启动判据,如式(9)所示,判据经或门输出,既保证可靠启动,又避免频繁的故障检测。

(9)

式中:up、un分别表示正、负极电压故障分量;K1set与K2set为整定阈值。选取K1set=500 kV/ms,K2set=30 kV。当连续三个采样点均满足启动判据,保护才启动。

本保护采用正、负极故障电压累加值之比来实现故障选极,定义比例系数K3如下:

(10)

式中:K3set为大于1的常数,按照躲过区内末端发生接地故障时的K3最小值进行整定,并留有一定的裕度,最终根据仿真取得较为可靠的大小,选取K3set=2。

3.3 故障识别判据

由3.1节的分析可知,利用修正电压可以较灵敏地对故障进行区分,且通过积分可以进一步扩大故障间的特征差距,有利于准确识别故障。定义故障识别判据,如式(11)所示。

(11)

式中:W1是数据窗长T内修正电压uxz绝对值的累加和;N1为T内的采样点数。为防止保护误动,本判据连续动作5次,保护才动作。当W1大于等于整定阈值W1set,表明发生区内故障。

在线路上发生区内故障时,初始行波穿过MMC边界,进入背侧线路的折射波经过背侧线路另一侧的MMC反射回到保护安装处后,在一定程度上削弱了修正电压的故障特征。为了保证保护的高灵敏度,判据的数据窗应躲过初始行波在本侧线路对端产生的反射波或在背侧线路产生反射波到达保护安装处的最短时间,因此数据窗口T应满足以下条件:

T≤min{2l/v,2lijxl/v}

(12)

式中:l为故障线路长度;lijxl为保护Pij相邻线路的长度;v为线模波速度,一般取2.95×108m/s。以Line41为例进行说明,在综合考虑保护的可靠性和速动性的前提下,最终选取数据窗长T=0.5 ms。

3.4 方向判据

为了防止基于电压的单端量保护出现在反向区外的近端发生故障时可能会误动的情况,提出一种新的方向元件,以准确识别反向区外故障。图9为线路Line41中点f2处发生金属性短路故障时,保护P14、保护P12、母线保护Pm处的1模故障电压u14、u12、um的故障初期理论波形。在行波到达MMC1边界后,由于限流电抗器L14的分压,保护P14处的电压u14的幅值大于母线侧电压um的幅值;而当折射波进入相邻线路Line12后,限流电抗器L12将吸收部分能量,大大降低了P12处的电压u12的幅值和陡度,于是数毫秒内非故障线路Line12上P12处的电压幅值小于母线处um的电压幅值。

图9 Line41上f2处故障u14、um及u12的计算波形图

图10为线路Line41的中点发生正极接地故障保护P12、P14及母线保护Pm安装处的故障电压和修正电压波形对比图。

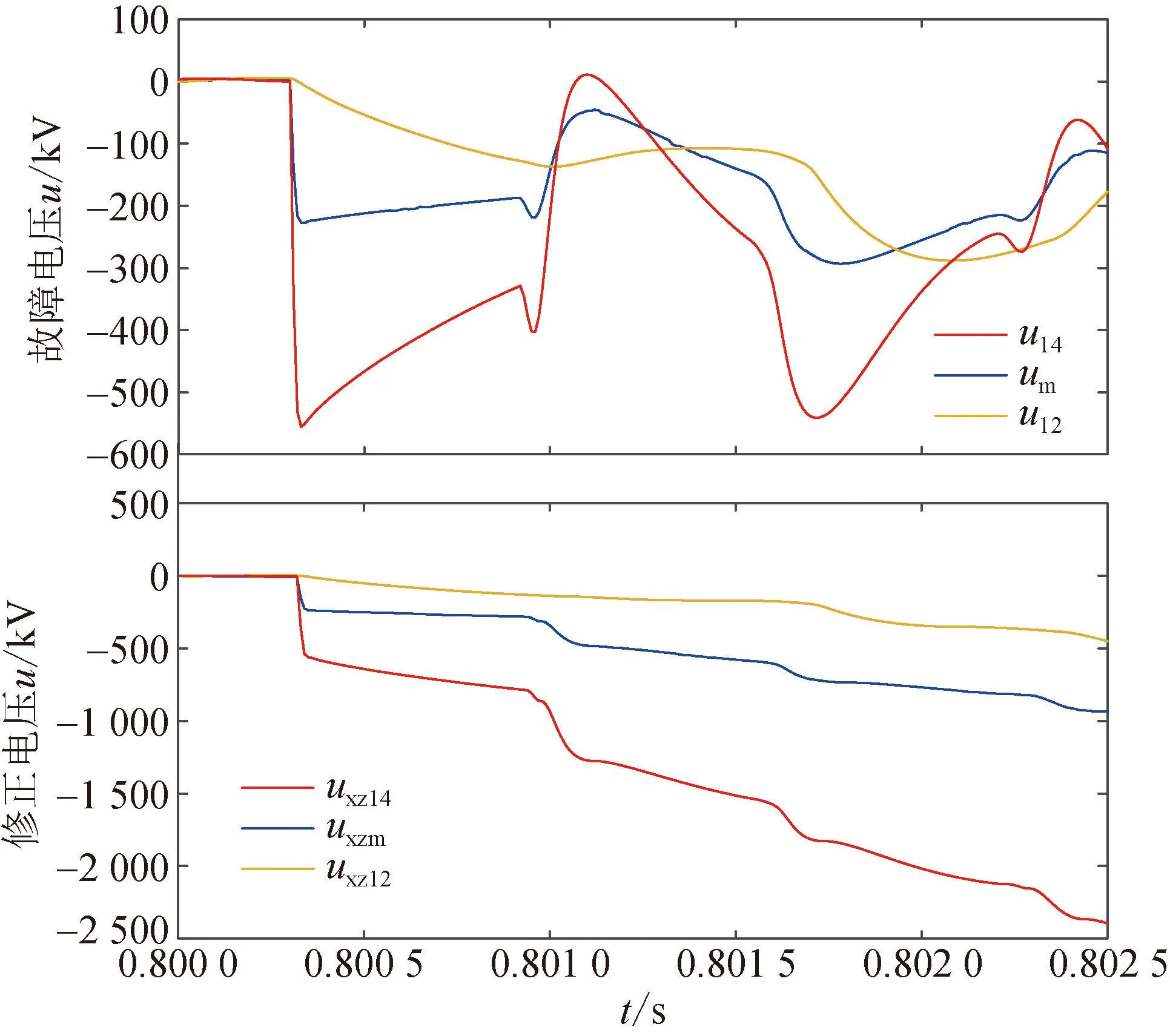
图10 Line41上f2处故障P12、P14及Pm处的故障电压、修正电压波形图

由图10可知,该故障对于P14是正向故障,线路侧修正电压uxz14大于母线侧修正电压uxzm;该故障对于P12是反向故障,母线侧修正电压uxzm大于线路侧修正电压uxz12。根据正、反向故障下方向特征这一质的差别,定义一种新的方向元件:

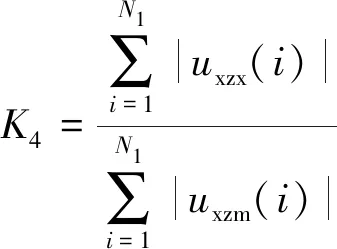
(13)

式中:uxzx(i)、uxzm(i)分别为限流电抗器的线路侧、母线侧修正电压;K4>1为正向故障,K4<1为反向故障。

故障选择判据的整定阈值要尽可能躲开区外故障,由于方向元件的作用,保护只需准确区分区内与正向区外故障即可。因此大大降低了单端量保护的整定难度,并相对提高了故障识别元件的灵敏度。

3.5 雷击闭锁判据

雷击输电线路的概率比较高,为避免保护在雷击干扰下误动,必须设计雷击闭锁判据。自然界中的雷电流多为负极性脉冲波,利用如式(14)所示的1.2/50 μs负极性双指数雷电流模型模拟雷电干扰[41]。其标准雷电波一般如图11所示,其中,T1=1.2 μs为(视在)波前时间,T2=50 μs为(视在)半峰值时间。

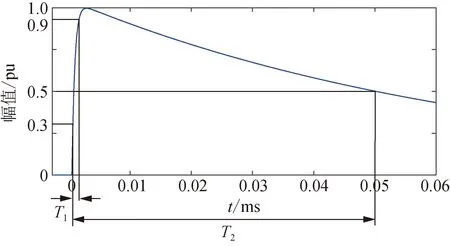
图11 标准雷电流的波形图

i(t)=ΛI0(e-αt-e-βt)

(14)

式中:I0为雷电流幅值;Λ、α与β为雷电流波的形状参数。

雷击干扰下,电压故障分量迅速衰减,通常在极短时间内(100 μs)就已经衰减得很小,所以在较长时间窗长T3内电压故障分量的平均值很小(此窗长仍取0.5 ms);而短路下故障电压的波动较大,衰减较慢,所以在T3内的平均值较大。据此,在一定时窗内,定义故障电压1模分量的衰减系数K5,如式(15)所示。

(15)

式中:u1(i)为保护安装处故障电压1模分量;N2为防雷判据时间窗长T3内的采样点数。

设计雷击闭锁判据为:

(16)

式中:K5set为雷击闭锁判据的整定阈值,应躲过常见雷击干扰下的最小K5,通过大量仿真,最终选取K5set=0.55。当K5大于等于整定阈值时,表明发生雷击干扰,闭锁保护。

3.6 后备保护原理

利用3.4节的方向元件提出一种纵联方向后备保护,以可靠识别区内高阻故障。由前文可知,当K4大于1时,表明正方向发生故障,定义方向信息H为:

(17)

式中:W′1set为后备保护的整定阈值,应躲过正常运行情况下线路上可能出现的最大W1,通过大量仿真并留有一定的裕度,最终选择W′1set=2 000 kV。

假设线路两端的测量点分别为m和k,下式为后备保护的故障选择判据。

(18)

式中:Hm、Hk分别表示m、k点的方向信息。

考虑到通信需要时间,且故障位置的变化会影响故障行波传播到线路两端的时间,所以后备保护的动作时限tact为:

tact=lc/vs+ll/vw+tDW+tx

(19)

式中:lc、ll分别为通信信道长度和传输线路长度;vw、vs分别为1模行波和信号的传播速度;tDW、tx分别为保护所需数据窗和光电转换、测量延时等所需时间总和。

以最长线路l23(211.3 km)为例计算后备保护动作时间,假设通信信道长度为1.5倍线路长度,tx设为0.1 ms,vw取295 km/ms,vs取200 km/ms[42],故障行波传到对端用时约0.72 ms,信号传输用时约1.58 ms,tDW为0.5 ms,共用时2.9 ms,仍小于3 ms。

3.7 保护流程

根据3.2—3.6节的分析,可绘制保护流程图,如图12所示。保护启动后,利用滤波算法处理故障信号,并进行极模变换。然后,判断是否发生雷击,若未发生雷击,则根据式(13)判断故障可能发生的方向,若判定为正方向故障,接着利用式(11)计算故障识别判据,若判定为区内故障,则利用式(10)进行故障选极;否则,认定为区外故障,主保护不动作,并等待后备保护的判别结果,若判断故障发生于区内时,接着进行故障选极。最后,根据选极判据结果选择正确的故障极,实现保护正确出口,切除故障。

图12 保护流程图

4 仿真验证

为验证本文所提出新型保护原理的可行性,在PSCAD/EMTDC仿真平台上搭建四端双极对称柔性直流系统模型,其系统拓扑及线路长度如图1所示,表1为直流系统的主要参数,其中换流器的子模块拓扑为半桥式结构。以线路Line41上的保护P14为例,研究不同位置发生故障时本保护原理的动作性能,故障位置如图1所示。本方案的采样频率为100 kHz,本方案W1set应躲过正向区外故障时的最大W1max,通过仿真得到正向区外短路故障时出现的W1max=0.965×104kV,并保留一定的裕度,最终设置整定阈值W1set=1.150×104kV。

表1 各MMC的主要参数

4.1 区内故障验证

表2为在线路Line41的不同位置发生经不同过渡电阻的正极接地短路故障的仿真结果,故障时刻均为0.8 s。由表2可得,区内金属性短路故障时的W1均远大于W1set,说明了本保护可以正确识别区内故障。区内故障时,主保护判据在距MMC1 3 km以上的线路能够耐受300 Ω的过渡电阻。方向元件在不同位置发生经600 Ω过渡电阻正极接地短路故障时均能正确动作,因此基于其构成的后备保护可以准确地识别区内故障。

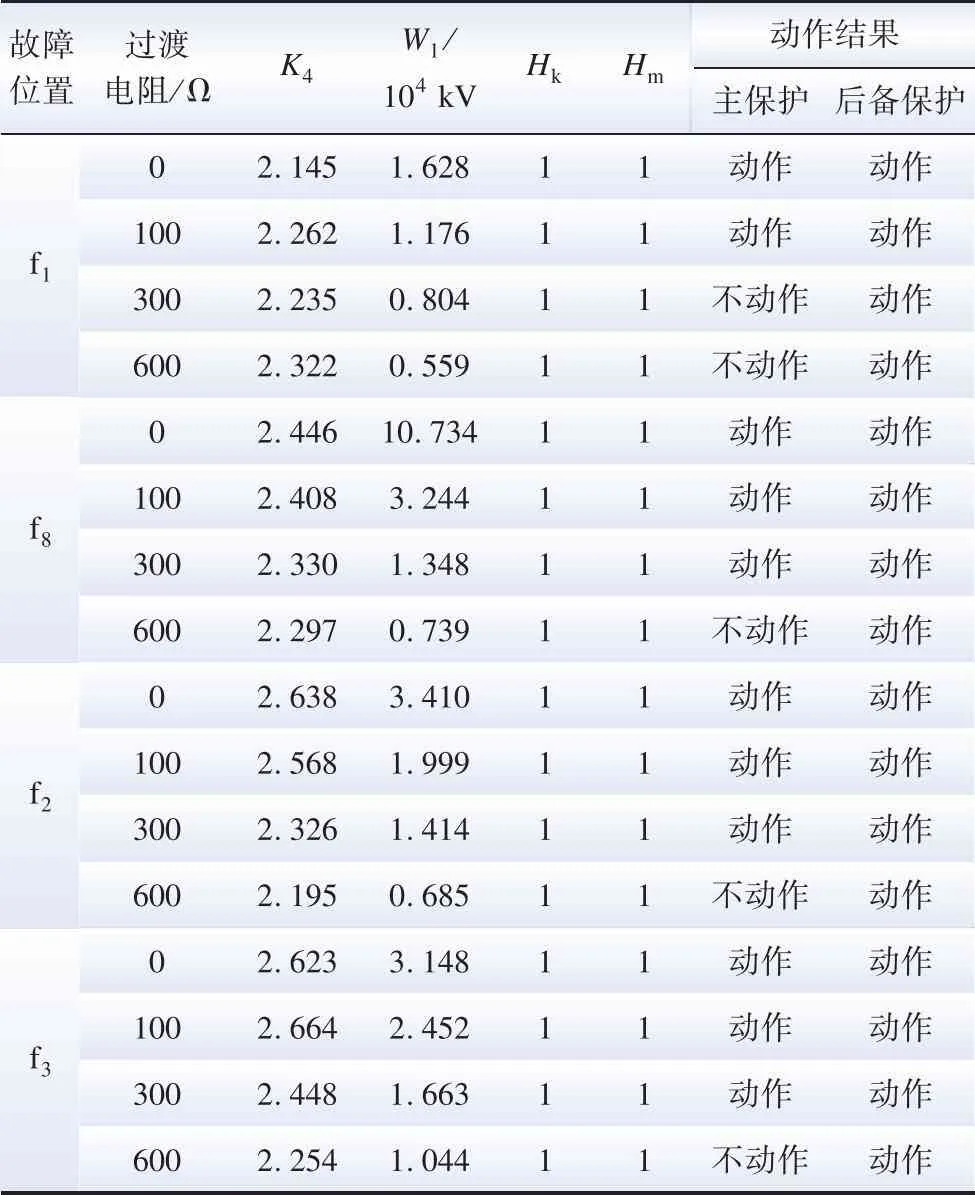
表2 区内不同故障位置下各保护判据的动作结果

短路故障发生在保护安装处的近端时,行波的折反射几乎不发生在故障点与线路边界之间,导致保护安装处的电压变化率偏低,进而大大降低了主保护判据的灵敏度,主保护甚至存在拒动的情况,在高阻接地故障的场景下主保护拒动的情况尤为严重。虽然主保护在近端高阻故障下拒动,但后备保护不受故障位置和过渡电阻的影响,均能正确动作,所以在双重保护的共同作用下,本方案仍能准确、可靠地识别故障。

表3为在直流输电线路Line41的不同位置发生正极、负极和极间故障的选极判据的动作结果。从表中可以看出:正极故障时,K3远大于2;负极故障时,K3远小于0.5;极间短路故障时,K3接近于1,证明了本方案选极判据的正确性。

表3 不同故障类型下选极判据的动作结果

4.2 区外故障验证

表4为不同位置的区外金属性短路故障下各保护判据的动作结果。由表可得,反向区外故障时,K4<1,保护元件不动作;正向区外故障时,K4>1,但W1小于整定阈值,判别为正向区外故障,保护元件不动作,本方案可以准确区分区内故障和区外故障。

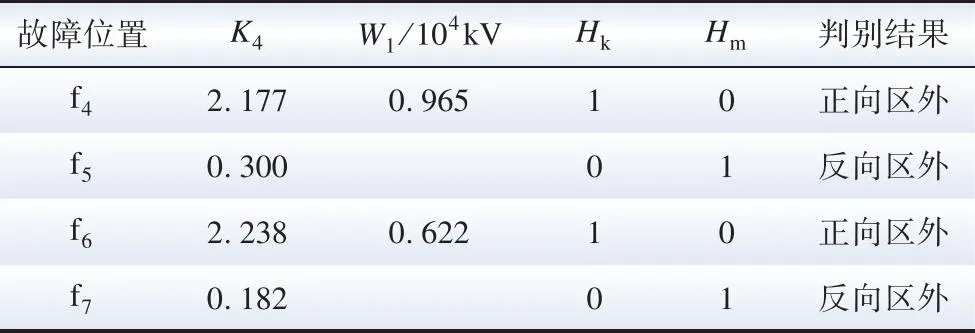
表4 不同区外故障下各保护判据的动作结果

4.3 雷击干扰验证

表5为在线路Line41上不同位置施加雷击干扰与短路故障时保护P14闭锁情况。

表5 雷击干扰与短路故障下防雷判据的判别结果

表6为在线路Line41中点施加雷电流为10 kA的不同雷电波的雷击干扰下的雷击判据的结果。由表5、表6可得,故障时,K5均小于0.55;而雷击干扰时,K5均大于0.55,故本文所提雷击闭锁判据能够准确识别雷击干扰和短路,本保护方案不会因雷击干扰而误动作。

表6 不同雷击电流波形下的防雷判据的判别结果

4.4 噪声干扰验证

小波滤波等算法具有较高的精度,能较好地剔除干扰信号。利用滤波算法对故障信号进行滤波,得到纯粹的故障波形再进行故障识别,可以减小噪声干扰对本保护方案的影响。本方案采用小波算法进行滤波,图13为电压信号滤波前后的对比图。由图可得,滤波后的电压波形与原始波形高度一致,大大降低了噪声干扰引起保护误动的可能性。

图13 电压信号滤波前后的效果对比图

表7为将信噪比为20 dB的高斯白噪声添加在不同位置短路故障下的电压信号中,经小波滤波算法滤波后,本保护方案各种判据的动作结果。由表可知,在较大的噪声干扰下,本方案仍能正确识别故障,具有较好的鲁棒性。

表7 噪声干扰下保护判据的动作结果

5 结 论

本文分析了区内末端与正向区外故障的特征差异,设计了电压修正算法,提出了一种基于修正电压的新型暂态量保护原理作为主保护,并基于线路两端的方向信息形成后备保护,形成了一套完整的主、后备保护方案。本保护方案具有一定的抗干扰能力和耐受过渡电阻的能力,且不依赖于成本较高且误差较大的行波波头捕捉。此外,由于本方案仅对电压信号进行简单运算,计算量小,因此大大降低了对数据采样和数据处理的硬件要求,符合工程实际应用的要求。