Hossfeld 模型在矿区地表动态沉降预测应用的可行性分析

赵 月，王志伟，张国建，王 翔，丁文壮

（山东建筑大学测绘地理信息学院，山东 济南 250101）

0 引言

地下煤矿开采活动打破开采工作面原有应力平衡，导致岩体发生移动变形，极易诱发地质灾害问题，威胁人民生命财产安全[1-2]。因此，研究矿区地表沉降规律对评估该地区潜在地质灾害风险至关重要。为准确评估煤矿开采对地表沉降的影响程度，需要先在工作面上建立地表动态沉降预测模型，获取模型未知参数，进而分析地表任意点、任意时刻的沉降变化[3]。时间模型是目前应用较为广泛的矿区地表动态沉降规律研究方法之一[4-7]。

矿区动态沉降过程一般分为三个阶段：初始期、主要期和残余期，沉降曲线形状呈“S 型”增长[8]。因此，为描述矿区沉降过程多采用“S 型”时间模型，如Knothe 函数[9]、Logistic 模型[10]和Usher 模型[11]等。然而，典型的时间模型中，由于自身特性的原因，导致其形状曲线不经过坐标原点（即：当t=0 时，沉降量、速度和加速度不全为0）[12]，这一点不能完全符合煤矿开采沉降特征。通常，针对这一问题，可以通过修正时间零点提高预测精度，但这种修正方式具有一定的经验性。目前，用来开展林木生长规律研究的Hossfeld 模型[12-13]，从模型形态上来看也属于“S 型”曲线，且函数经过坐标原点，符合矿区沉降特征，可以尝试用来进行矿区地表动态沉降规律研究。乔思宇等[12]基于AIC 准则评价Hossfeld 模型，分析该模型在煤矿区地表动态沉降预测中的可靠度。除此以外，在以往的研究中，学者们利用水准数据对矿区进行单点地表动态沉降预测，这种少量水准数据具有偶然性，无法证明模型适用于矿区全盆地任意点，针对这一问题，杨泽发等[14]基于InSAR 时序沉降，利用Logistic 模型分析矿区全盆地沉降时空演化规律，充分发挥InSAR 技术高分辨覆盖率特点，探索Logistic模型参数分布规律。

本文针对典型时间模型存在时间零点问题，采用Hossfeld 模型，分别利用菏泽某矿区水准监测数据和门克庆某矿区D-InSAR 累积沉降量数据，通过与两种典型时间模型（Usher 模型和Knothe 模型）进行对比，分析采用Hossfeld 模型进行矿区单点和任意点地表动态沉降预测的可行性分析。一方面，在基于水准监测数据分析时间零点对典型时间模型影响的基础上，采用均方根误差（Root Mean Square Error，RMSE）和平均绝对误差（Mean Absolute Error，MAE）对三种时间模型单点沉降预测精度进行评价，探讨不同模型单点预测的适用性；另一方面，基于DInSAR 累积沉降量数据，根据D-InSAR 获取高分辨沉降监测结果的优势，研究Usher 模型、Knothe 模型和Hossfeld 模型参数相关性，探讨利用少量点实现全盆地任意点沉降预测的可行性，并在此基础上，采用RMSE、MAE、Bland-Altman 图分别对三种时间模型全盆地任意点地表动态沉降预测精度进行评价，对比验证了不同模型在矿区全盆地任意点动态沉降预计中的适用性和可行性。

1 原理与方法

1.1 矿区开采沉陷规律

由煤矿开采引起的矿区地表动态沉降是一个复杂的过程，大致可以分为三个阶段：初始沉降期、主要沉降期和残余沉降期，如图1 所示。①初始沉降期：随着地下煤炭资源开采地表上覆地某一点会发生位置变化，此时t=0、v=0、ɑ=0、w=0，当地下开采影响该点时，t＞0，该点逐渐产生沉降，沉降量逐渐增大，速度和加速度也逐渐增加，此阶段沉降量较小；②主要沉降期：沉降量随着时间的推移迅速增大，速度随时间增大至峰值然后减小，加速度也随时间增大到极值然后减小至相对应的负值，此阶段地表沉降达到充分采动状态或超充分采动状态，沉降范围达到最大；③残余沉降期：速度逐渐减小至0，加速度也逐渐由负值减小至0，沉降量缓慢增加直至达到极限值趋于稳定，此阶段持续时间最长。由图1（a）可知，沉降量满足“S”型曲线，但曲线为非对称性线形，曲线前端短、后端长，且单调递增。除此之外，由于矿区不同地质采矿条件，使煤矿开采过程存在差异，曲线表现为近“S”型，可通过调整参数改变曲线的陡峭程度[3]。

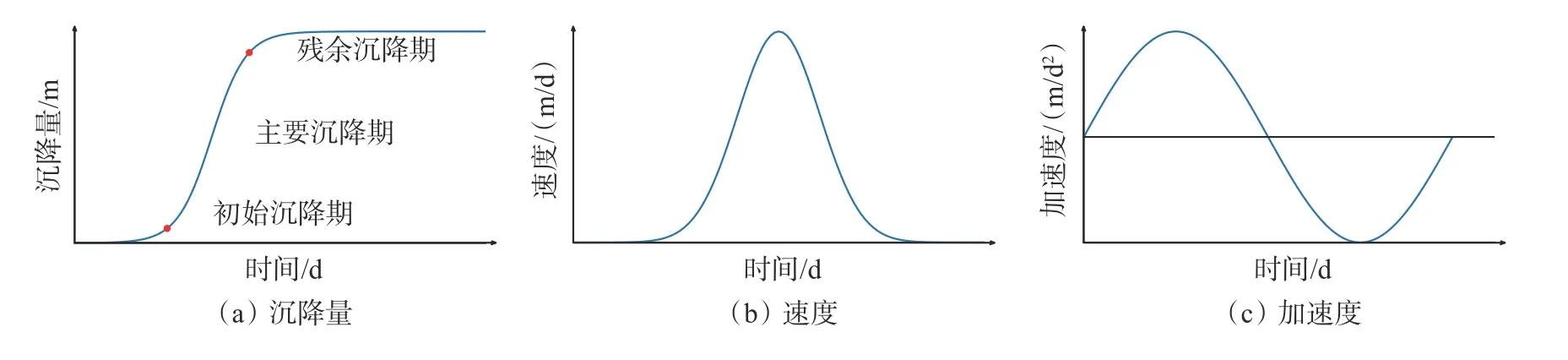
图1 矿区某点沉降过程Fig.1 Subsidence process at a point in the mine

1.2 典型时间模型

作为典型“S”时间模型，Usher 模型和Knothe 模型均可以通过参数调节曲线形状，具有较强的适应性[15-16]。然而，它们都存在t=0 时，沉降量、速度和加速度不全为0 的情况，不符合矿区沉降初始规律。为此，本文根据这两个模型的沉降量表达式推导其对应的速度表达式和加速度表达式，并计算t=0 时，沉降量、速度和加速度特征，结果见表1。Usher 模型中，wm为最大下沉量；ɑ、b、c为沉降参数。当t=0 时，w≠0，v≠0，a≠0，不符合沉降初期规律。Knothe模型中，当t=0 时，w（t）=0，v（t）≠0，a（t）≠0，不满足沉降初期，沉降量、速度和加速度都为0 的规律。

表1 Usher 模型和Knothe 模型沉降特征Table 1 Subsidence characteristics of Usher model and Knothe model

1.3 Hossfeld 模型

Hossfeld 模型是一种常用的理论生长模型[12-13]，可表示为式（1）。

式中：w（t）为t时刻的下沉量；wm为最大下沉量；ɑ和b为沉降参数。对式（1）进行一阶求导可得速度公式，二阶求导可得加速度公式，其表达式分别为式（2）和式（3）。

由式（1）～式（3）可知，当t=0 时，w（t）=0，v（t）=0，a（t）=0 ；当t=+∞ 时，w（t）=wm，v（t）=0，a（t）=0。进一步分析发现，参数ɑ代表时间的幂次方对沉降量的影响程度，当ɑ＞1 时，时间的影响更加显著，w对t的响应会更快；当0＜ɑ＜1 时，时间的影响较小，w对t的响应会相对缓慢；参数b作为一个常数项，代表了时间对沉降量的影响程度，其会对公式中的分母部分进行调节，从而影响w的数值，但当参数b=0 时，w与wm相等，这表示wm是唯一影响w的变量；参数wm为最大沉降量。

为进一步探究Hossfeld 模型中不同参数对沉降量曲线的影响，模拟不同参数取值下沉降结果曲线，如图2 所示，其中，在图2（a）中，ɑ分别为2.6、2.8、3.0、3.2 和3.4，wm=1 000 mm，b=1 000；在图2（b）中，b分别为50、500、1 000、2 500 和5 000，wm=1 000 mm，ɑ=3。从图2 中可以看出，参数ɑ越大，到达最大沉降量的时间越短，曲线弯曲程度越大，也更加陡峭；参数b越大，到达最大沉降量时间越长，曲线弯曲程度越小，也更加平缓。综上所述，从模拟的曲线来看，Hossfeld 模型符合矿区沉降曲线前端短后端长且单调递增的特征；且Hossfeld 模型未知参数的大小对曲线拟合程度有较大影响，需要选择合适的参数才能准确拟合矿区开采沉降过程。

图2 Hossfeld 模型沉降参数对曲线的影响Fig.2 Influence of parameters on the subsidence curves for the Hossfeld model

2 联合水准数据的矿区开采单点动态沉降预测

2.1 研究区概况

选取菏泽某矿为研究区（图3）。图3 中部圆圈标记部分为自南向北的走向线水准点，共86 个。水准数据时间跨度为2016 年12 月2 日—2018 年2 月27 日，时间周期最短间隔7 d，最长间隔43 d，总共观测18 次。

图3 研究区概况Fig.3 Overview of the study area

2.2 时间零点对典型时间模型沉降预测精度影响

为了说明时间零点对典型时间模型沉降预测精度影响，本文以实测水准数据为数据源，以Usher 模型和Knothe 模型为例，分别开展修正时间零点和未修正时间零点实验，其中，修正时间零点阈值为2 cm。选取研究区范围内任意一点的水准观测沉降值，采用遗传算法（Genetic Algorithm，GA）[17]对上述两种模型未知参数进行反演，根据反演出的参数构建Knothe 模型和Usher 模型并进行沉降值预测，预测结果如图4 所示。由图4 可知，由于零点的设置不同，导致样本点的拟合度存在差异，较多水准数据偏离拟合曲线，修正时间零点的模型明显优于未修正时间零点的模型。

图4 Knothe 模型和Usher 模型和预测结果拟合度对比Fig.4 Comparison of the fitting for the predictions of the Knothe model and the Usher model

本文以RMSE 和MAE 为评价指标，分别统计分析全部样本点所有预测值与实测值差值。考虑到选用的水准数据累计沉降量部分已达2 000 mm，而对于沉降量级较大区域，预测值与实测值之间的差异通常较大，因此，选择100 mm 为评价指标阈值，结果见表2。由表2 可知，在Usher 模型沉降预测结果中，在＜100 mm 范围的RMSE 和MAE，未修正时间零点的Usher 模型精度低于修正时间零点的Usher 模型，经过修正时间零点后的模型精度分别提高2.33%和3.49%。在Knothe 模型沉降预测结果中，经过修正时间零点的模型精度分别提高4.63%和3.49%。综上所述，对于Usher 模型和Knothe 模型而言，设置合适的时间零点会提高预测精度。然而，在面对不同地质条件的矿区时，单纯从模型公式出发，很难给出统一的标准来修正时间零点。因此，对于时间零点的修正问题，经验性因素起着至关重要的作用。

表2 修正和未修正时间零点模型预测值与水准数据实测结果对比Table 2 Comparison of predictions of corrected and uncorrected time-zero model and results of leveling data 单位：%

2.3 不同时间模型沉降预测精度对比

为了弥补典型时间模型需要修正时间零点这一缺陷，采用无需修正时间零点的Hossfeld 模型。同样以2.2 部分水准数据为数据源，采用GA 进行未知参数反演，根据反演参数构建Hossfeld 模型，并进行沉降值预测。通过RMSE 和MAE 这两个评价指标探究基于Hossfeld 模型对矿区开采沉降预测结果精度，结果见表3。由表3 可知，采用Hossfeld 模型进行沉降预测结果的绝大部分样本点误差较小。对比表2来看，在＜100 mm 的范围内的RMSE，Hossfeld 模型沉降预测精度比经过修正时间零点的Usher 模型沉降预测精度降低1.16%，比未经过修正时间零点的沉降预测精度提高1.17%，比经过修正时间零点和未经过修正时间零点的Knothe 模型沉降预测精度分别提高25.28%和30.24%，说明Hossfeld 模型预测精度略低于修正时间零点的Usher 模型，高于未修正时间零点的Usher 模型，远远高于修正时间零点和未修正时间零点的Knothe 模型；在＜100 mm 的范围内的MAE，Hossfeld 模型沉降预测精度比经过修正时间零点和未经过修正时间零点的Usher 模型的沉降预测精度分别提高3.49%和6.98%，比经过修正时间零点和未经过修正时间零点的Knothe 模型的沉降预测精度分别提高33.72%和37.21%，说明Hossfeld 模型沉降预测精度均高于Usher 模型和Knothe 模型。

表3 Hossfeld 模型预测值与水准数据实测结果对比Table 3 Comparison of predictions of Hossfeld model and results of leveling data 单位：%

此外，从上述的原理与方法中，可知Usher 模型需要反演四个未知参数，而Hossfeld 模型只需要反演三个未知参数，降低了模型的复杂度；Knothe 模型虽然只有两个未知参数，模型复杂度降低，但是模型精度有所降低。因此，相较于Usher 模型和Knothe 模型，Hossfeld 模型无论是在精度还是模型复杂度上，都具有一定优势。

3 联合D-InSAR 的矿区全盆地开采任意点动态沉降预测

3.1 D-InSAR 累积沉降监测

选取内蒙古自治区门克庆某煤矿为研究区（图5），图5 图中长方形框为Sentinel-1A 数据覆盖范围。选取的SAR 影像时间跨度为2017 年10 月2 日—2018 年5 月30 日，具体参数见表4。该地区地处干旱与半干旱过渡地带，土地沙漠化和水土流失较为严重，植被覆盖率较低，因此，Sentinel-1A 数据受空间失相干影响较小[18]。利用D-InSAR 技术对11 景覆盖研究区的影像进行两两差分干涉处理，其中，两两干涉处理的干涉对，主影像为前一个时间的影像。基于轨道信息对影像先进行粗配准，再基于频谱差异法精配准，通过不断迭代，直到达到0.001 像素[19]。通过多视处理消除由单个像元散射的雷达回波信号相干叠加导致强度信息的大量噪声[20]，并采用自适应滤波方法[21]进一步消除噪声影响。采用最小费用流法[22]对消除噪声后的缠绕相位进行相位解缠，并将解缠后的相位转换为雷达视线方向的沉降量，最后通过地理编码得到地图坐标系下的沉降量。数据处理过程中，采用在美国国家航空航天局（National Aeronautics and Space Administration，NASA）获得的30 m 分辨率的SRTM DEM 数据来消除地形相位的影响[23]，通过欧州航天局（European Space Agency，ESA）提供的POD 精密轨道数据（Precise Orbit Ephemerides）来消除轨道误差带来的误差[24]。

表4 影像参数Table 4 Parameters of the SAR imaging

图5 研究区概况Fig.5 Overview of the study areas

图6 为矿区2017 年10 月2 日—2018 年5 月30日部分累积沉降结果。随着地下煤炭不断开采，地面沉降的量级和影响范围都不断扩大，造成如图6所示的沉降盆地中心出现空白区域，一方面是因为矿区大沉降梯度的特点，导致矿区中心地表沉降超过Sentinel-1A 影像可监测的沉降范围[25]；另一方面，SAR 影像的波长与分辨率决定了可监测最大沉降梯度，而本文选择的Sentinel-1A 影像波长本身较短，且为去除斑点噪声，对影像进行多视处理，导致像元分辨率降低，进一步限制可监测最大沉降梯度的范围[26]。为了验证D-InSAR 技术监测结果的可靠性，收集了图6（c）中黑点所示的水准监测数据，其中，走向线自东向西为MA1 号水准点～MA38 号水准点，共38 个，倾向线自北向南为MD1 号水准点～MD18 号水准点，共18 个。除空白区域外，共有14 个水准点与DInSAR 监测结果位置相重合。图7 为水准数据沉降量与D-InSAR 累积沉降量的差值对比图。由图7 可知，在MA 线上水准点与D-InSAR 结果在边缘处有八个点重合，最大差值不超过23 mm；在MD 线上有六个点重合，其中，有三个点在边缘处，最大差值不超过38 mm，还有三个点在中心位置重合，最大差值不超过280 mm。由此可见，矿区边缘处差值较小，D-InSAR 精度较为可靠，而矿区中心位置差值较大，已超出D-InSAR 沉降监测范围，结果不可靠。后续时间模型参数求解过程中以沉降边缘区域数据为主。

图6 部分D-InSAR 累积沉降结果Fig.6 Partial cumulative subsidence results from D-InSAR

图7 水准数据沉降量与D-InSAR 累积沉降量的差值对比Fig.7 Difference between the subsidence from leveling data and D-InSAR

3.2 矿区全盆地任意点预测过程分析

为利用少量地表点的监测数据实现矿区全盆地任意点沉降预测，需要探究时间模型未知参数内在规律，本文选用相关系数作为评判标准，取值范围为-1 到1，当接近1 时，表示存在强正相关关系；当接近-1 时，表示存在强负相关关系；当接近0 时，则表示两个变量之间几乎没有线性关系。通过对上述三种时间模型的全部模型参数进行统计，在Usher 模型中，将未知参数ɑ作为自变量，参数b作为因变量，获取的相关系数为4.21×10-3；将未知参数ɑ作为自变，参数c作为因变量，获取的相关系数为7.64×10-3；将未知参数b作为自变量，参数c作为因变量，获取的相关系数为0.425，相关性低。在Hossfeld 模型中将参数ɑ作为自变量，b参数作为因变量，ɑ的取值范围从0.730 到3.650，b的取值范围从0.210 到1 000，获取的相关系数为0.796。在Knothe 模型中，将参数ɑ作为自变量，b参数作为因变量，ɑ的取值范围从106.650 到652.268，b的取值范围从4.99×10-3到0.005，获取的相关系数为-0.158。三种模型中，Hossfeld 模型未知参数相关系数最高，更有可能用少量地表点的监测数据实现任意点的动态预计。

将D-InSAR 技术获取的矿区累积沉降量作为数据源，利用GA 分别建立修正时间零点的Usher 模型和Knothe 模型，其中，时间零点阈值为3 cm，以及无需修正时间的Hossfeld 模型。选择2018 年5 月30 日预测的所有样本点统计Bland-Altman 图，结果如图8所示。由图8 可知，绝大部分样本点都位于上下限内，部分点出现偏离（图8 中椭圆圈出部分），主要原因为GA 算法反演参数时过早收敛，陷入局部最优解，导致预测值存在偏差。总体而言，Hossfeld 模型上下限范围明显小于Usher 模型和Knothe 模型，说明预测得到结果差别较小，表示预测结果一致性越高。

图8 Bland-Altman 图Fig.8 Results of the Bland-Altman

表5～表7 分别给出了Usher 模型、Knothe 模型和Hossfeld 模型预测沉降量与D-InSAR 累积沉降量的RMSE 和MAE 分布情况，Usher 模型和Hossfeld 模型的预测样本点精度较高，而Knothe 模型的预测样本点精度相对较差。综合分析发现，在＜20 mm 范围内，Hossfeld 模型较Usher 模型和Knothe 模型在RMSE 和MAE 比例中分别提升2.55%、2.55%、88.99%和75.12%。

表5 Usher 模型沉降预测结果与D-InSAR 沉降结果对比Table 5 Comparison of Usher model subsidence prediction results and D-InSAR subsidence results

表6 Knothe 模型沉降预测结果与D-InSAR 沉降结果对比Table 6 Comparison of Knothe model subsidence prediction results and D-InSAR subsidence results

表7 Hossfeld 模型沉降预测结果与D-InSAR 沉降结果对比Table 7 Comparison of Hossfeld model subsidence prediction results and D-InSAR subsidence results

综上所述，Knothe 模型在描述矿区全盆地沉降方面的精度较低，而Usher 模型和Hossfeld 模型的预测精度相对较高。进一步对比发现，相比于Usher 模型，Hossfeld 模型预测矿区沉降结果精度略高。

4 结论

本文针对Usher 模型和Knothe 模型存在时间零点问题，采用Hosfeld 模型，基于水准数据和D-InSAR数据，构建时间模型，探讨不同模型在矿区开采沉降过程中预测精度，得出结论如下所述。

1）通过水准数据验证，相较于未修正时间零点的Usher 模型和Knothe 模型，在＜100 mm 范围内Hossfeld 模型的RMSE 和MAE 有所提高；对于修正时间零点的Usher 模型和Knothe 模型，在＜100 mm 范围内Hossfeld 模型的RMSE 和MAE 高于Knothe 模型，与Usher 模型相当。

2）通过D-InSAR 技术获取大量地表累积沉降量数据，来统计 矿区Hossfeld 模型、Usher 模型和Knothe 模型任意点未知参数并分析未知参数相关性，Hossfeld 模型相干性最高；通过RMSE、RMAE 和Bland-Altman 图三种评价指标发现，Hossfeld 模型预测矿区任意点动态沉降在精度方面具有优势。

3）相较于Usher 模型，Hossfeld 模型少了一个未知参数，降低了模型复杂性的同时可以获取相当的预测精度；相较于Knothe 模型，Hossfeld 模型多了一个未知参数，但可以提升预测精度。