木勺生产线机械臂的动静特性及结构优化
2024-04-02翟庆磊曹文豪张庆功王锦添
赵 辉 翟庆磊 曹文豪 张庆功 王锦添 李 明
(东北林业大学机电工程学院,黑龙江 哈尔滨 150040)
随着2023 年《商务领域经营者使用、报告一次性塑料制品管理办法》的颁布,国家对于塑料制品的限制越来越严,同时鼓励餐饮行业使用木制品餐具代替一次性塑料制品,木制品餐具企业的订单数量不断增加。然而,目前中小型企业木勺生产线仍采用人工上下料的方式,工人劳动强度大,且工作效率较低。此外,由于木质餐具需要在高温下冲压制作,这使得人工上下料的作业方式非常危险。作为自动化设备,龙门式机械臂被广泛用于工厂车间,代替人工完成重复、枯燥且频繁的工作[1-4]。
本文拟根据工厂实际使用的冲压机(图1),以现有的龙门式机械臂为基础(图2),通过对其结构进行改进,设计可用于木勺生产线的机械臂。为确保机械臂顺利实现上下料功能,要求其在上下料过程中左右晃动幅度保持在2 mm以内。鉴于此,本文使用建模软件对初步设计的生产线机械臂进行三维建模处理,并运用建模软件与有限元分析软件的协同仿真技术对机械臂进行静态性能分析,确定其最不稳定的工况,并选取此工况进行动态性能分析,运用灵敏度分析机械臂的设计变量,筛选对其动静性能影响较大的设计变量。采用拉丁超立方抽样对选取的设计变量进行采样,分别运用Kriging模型与NPR模型构建近似模型,并采用MOGA法(多目标遗传算法)对设计的目标函数进行求解,实现对生产线机械臂的优化。

图1 冲压机结构Fig.1 Stamping machine structure

图2 生产线机械臂结构Fig.2 Structure of the robotic arm on the production line
1 静态分析
为节约计算的时间,忽略生产线机械臂模型中的倒角、螺纹等不重要细节,同时忽略对生产线机械臂动静性能影响不大,且不在本研究结构范围内的驱动电机、真空吸盘等部件[5-10]。简化后的生产线机械臂结构如图3 所示。
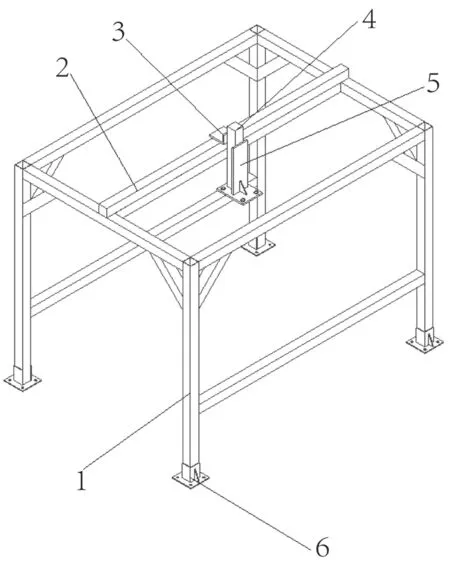
图3 生产线机械臂简化结构Fig.3 Simplified structure of the production line robotic arm
龙门架采用的材料为6061 铝合金,地脚采用的材料为HT200 灰铸铁,L型板与T型板采用的材料为1Cr13 不锈钢,水平与竖直移动机构采用的为45 号钢。材料的具体参数如表1 所示。

表1 材料具体参数Tab.1 Material specific parameters
根据生产线机械臂结构的对称性,可对其工况进行适当简化[3],可分为四种极限工况:
1)工况一:竖直移动机构处于水平移动机构边缘,且自身处于极限上工况;
2)工况二:竖直移动机构处于水平移动机构边缘,且自身处于极限下工况;
3)工况三:竖直移动机构处于水平移动机构中心,且自身处于极限上工况;
4)工况四:竖直移动机构处于水平移动机构中心,且自身处于极限下工况。
生产线机械臂在进行上下料作业时,所受到的外部载荷主要来源于木勺毛坯与真空吸盘,真空吸盘吸满木勺毛坯时的质量为11 kg。进行网格划分,同时以Force方式在T型板对应位置添加所受的力,并且在龙门架地脚位置添加对应的固定支撑。各个极限工况对应的应力如表2 所示。

表2 各个极限工况对应的应力Tab.2 Corresponding stresses for each extreme working condition
由表2 可知,当竖直移动机构处于水平移动机构中心,且自身处于极限上工况时,其应力值最大,此时的等效应力图与总变形图分别如图4 和图5 所示。

图4 等效应力图Fig.4 Equivalent stress diagram

图5 总变形图Fig.5 Overall deformation diagram
由图4 和图5 可知,生产线机械臂极限工况下最大应力发生在L型板底部,数值为1.938 8 MPa,最大变形发生在T型板,数值为0.043 3 mm。在提升安全系数的情况下,生产线机械臂需要满足的刚度与强度分别如下:
式中:fmax为生产线机械臂可以承受的最大静变形量,mm;[f]为所选材料的许用挠度,mm;L为T型板的长度,数值为196 mm。
式中:σmax为生产线机械臂在受到约束情况时的最大等效应力,MPa;[σ]为L型板所选材料1Cr13 不锈钢的屈服强度,数值为245 MPa;1.5 为所选的安全系数。
根据公式(1)和(2)可知,生产线机械臂在极限工况下仍然符合使用的要求,且安全余量很大。同时,该工况为理论上的最危险工况,其余工况的最大应力值与最大变形均小于该工况。因此,选取该工况下的模型进行下一步的动态分析研究。
2 动态分析
2.1 模态分析
为避免初步设计的生产线机械臂在上下料过程中出现共振问题,拟采用模态分析法[11-14]。
在有限元分析软件中,对简化后的生产线机械臂进行网格划分,同时,在龙门架地脚位置添加对应的固定支撑[15-16],将分析设置中的最大模态阶数调整成为10阶[17],求解后得出的前10阶固有频率如表3所示。
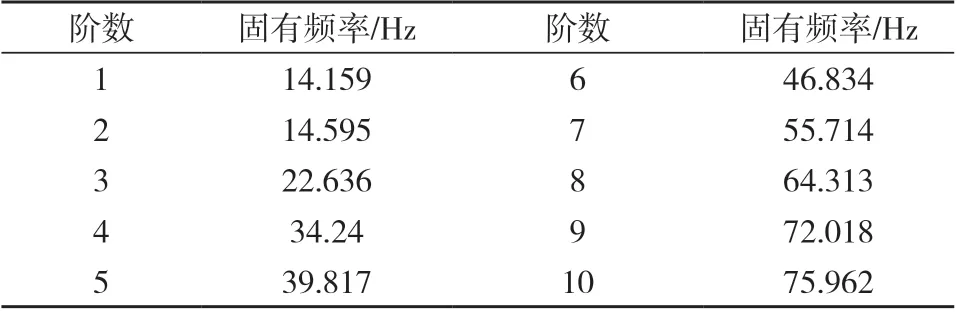
表3 前10 阶固有频率Tab.3 First 10 natural frequencies
在振动过程中,由于外力变化速度太快,模型来不及变形或者变形速度达不到外力变化的速度,导致在固有频率较低时模型变形程度较大。因此,本文选取前6阶模态进行重点研究[18]。
2.2 谐响应分析
为了更加精确地分析在施加外部载荷后,生产线机械臂的振动情况,需要对生产线机械臂进行谐响应分析[18]。
设置谐响应分析的最大频率为45 Hz,并且以Force方式在T型板对应位置添加所受的外部载荷[18]。图6为T型板在Y方向的振幅频率响应曲线。

图6 T型板在Y方向的振幅频率响应曲线Fig.6 Amplitude frequency response curve of T-shaped plate in the Y direction
从图6可知,在1~45 Hz频率的影响下,生产线机械臂的T型板在Y方向的位移最大为4.155 5 mm,对应的频率为34.244 Hz。然而,生产线机械臂在上下料过程中所允许出现的最大位移为2 mm,因此需要进行优化设计。
3 灵敏度分析与优化
为实现对生产线机械臂的优化,选择生产线机械臂的立柱、横梁、纵轴、L型板以及T型板进行研究。同一结构的参数分布如图7 所示,立柱、横梁与纵轴对应的厚度参数位置如图8 所示,L型板和T型板的参数位置分别如图9 和10 所示。

图7 同一结构的参数分布Fig.7 Parameter distribution of the same structure

图8 立柱、横梁与纵轴对应的参数分布Fig.8 Parameter distribution corresponding to columns,beams, and longitudinal axis

图9 L型板的参数分布Fig.9 Parameter distribution of L-shaped plate
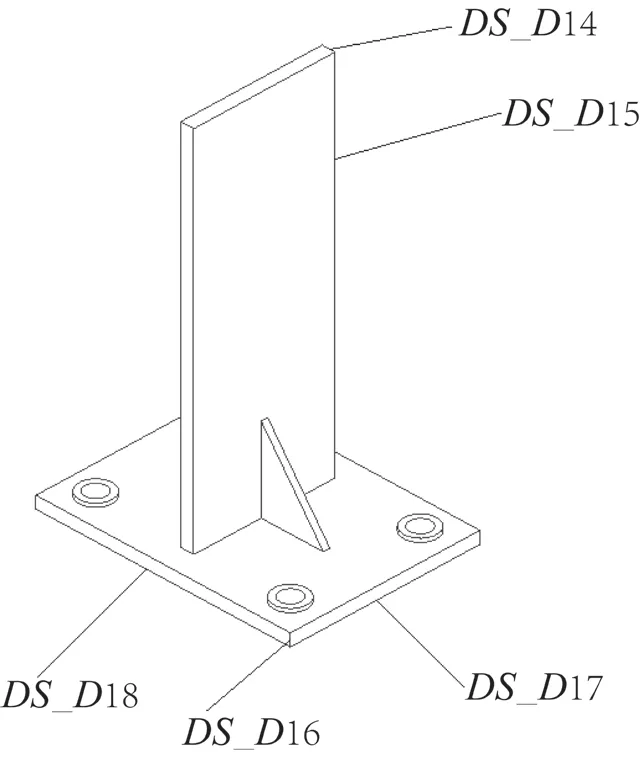
图10 T型板的参数分布Fig.10 Parameter distribution of T-shaped plate
利用有限元分析软件的Parameters Correlation模块,对各个初始设计变量进行计算,得出各个初始设计变量对于第四阶固有频率P19、生产线机械臂质量P20 以及Y方向最大振幅P39 的灵敏度,分别如表4、5、6 所示。

表4 变量对第四阶固有频率的灵敏度Tab.4 Sensitivity of variables to the fourth order natural frequency

表5 变量对质量的灵敏度Tab.5 Sensitivity of variables to mass

表6 变量对Y方向最大振幅的灵敏度Tab.6 Sensitivity of variables to the maximum amplitude in the Y direction
当第四阶固有频率与初始设计变量成正比时,灵敏度为正值;当第四阶固有频率与初始设计变量成反比时,灵敏度为负值。质量、Y方向最大振幅与初始设计变量的关系亦是如此。因此,为了尽可能优化生产线机械臂的性能,同时提高优化效率,选取灵敏度绝对值较大的初始设计变量进行优化[19-21]。
最终,选取DS_D1、DS_D2、DS_D3、DS_D4、DS_D5、DS_D6、DS_D7、DS_D8、DS_D9、DS_D10、DS_D11、DS_D13、DS_D14、DS_D16、DS_D17、DS_D18作为优化的对象。
在对生产线机械臂进行优化时,为确保样本分布均匀,并快速实现收敛,本文运用多维分层的拉丁超立方抽样,具体抽选样本点的过程如图11 所示。

图11 拉丁超立方抽样过程Fig.11 Latin hypercube sampling process
选取生产线机械臂设计变量作为输入,以第四阶固有频率、质量以及Y方向最大振幅作为输出,选取样本数量为140,随机生成器种子数量为10,通过求解,获得抽取的样本以及对应的输出。
4 建立近似模型
在实际计算过程中,使用生产线机械臂直接进行有限元优化不仅需要反复调用模型,效率低,而且容易出现错误。因此,为节约计算时间,提高优化效率,采用近似模型代替有限元分析。
考虑到生产线机械臂存在明显的非线性,运用Kriging模型以及NPR模型进行有限元分析。Kriging模型存在明显的平滑效应,可以为生产线机械臂进行无偏差预测[22],其表达式为:
式中:GKriging(D)为是近似模型;gT(D)为全局模拟的多项式计算函数;β为回归系数;Z(D)为是局部偏差。
NPR模型在使用时,不需要提前规定模型的形式,可以得到较宽的非线性预测,而且在进行总体估计过程中,不依赖分布形式,具有偏差小、置信区间精确等特点[23],其表达式为:
式中:Y为输出值;Pi为固定设计点;i为抽取样本的点数,i=1,…,m;m为总样本的点数;f(Di)是关于优化设计变量的均值函数;σ(Di)为关于优化设计变量的方差函数;εi为随机误差;Di是第i个设计变量。
将拉丁超立方抽样得到的样本数据分别运用Kriging模型和NPR模型构建生产线机械臂的近似模型。由于输入数据及输出数据较多,本文仅对比Kriging模型和NPR模型中的两组,其响应面如图12、13、14、15 所示。

图12 运用Kriging模型D1、D9、第四阶固有频率的响应面Fig.12 Response surface of Kriging model D1, D9, and fourth order natural frequencies
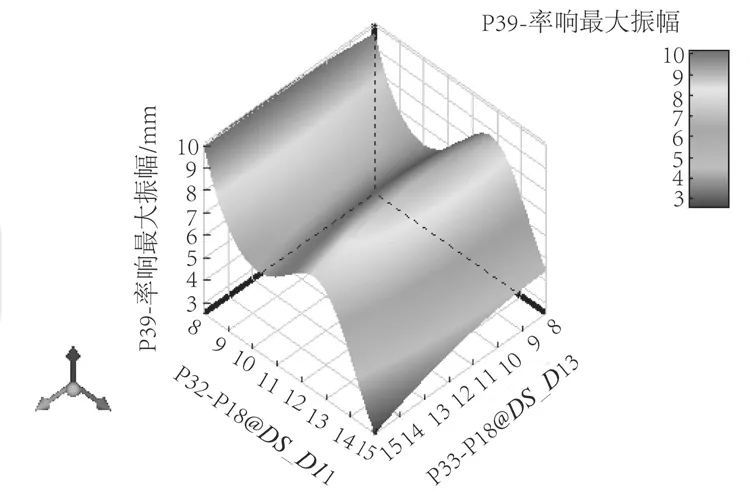
图13 运用Kriging模型D11、D13、最大振幅的响应面Fig.13 Response surface of maximum amplitude using Kriging models D11, D13

图14 运用NPR模型D1、D9、第四阶固有频率的响应面Fig.14 Response surface of NPR model D1, D9, and fourth order natural frequencies

图15 运用NPR模型D11、D13、最大振幅的响应面Fig.15 Response surface using NPR models D11, D13,and maximum amplitude
从图12~15 中可以看出,运用Kriging模型与NPR模型构建的生产线机械臂的近似模型具有一定区别,运用NPR模型构建的近似模型的响应面相对比较光滑,运用Kriging模型构建的近似模型的响应面边缘相对比较明显,可为生产线机械臂做出较好的预测。
为进一步检验运用Kriging模型与NPR模型构建的生产线机械臂近似模型能否反映实际模型,需要对其进行详细评估,评估参数包括测定系数、均方根误差、相对最大绝对误差等。测定系数表示符号为R2,最佳值为1;均方根误差表示符号为RMSE,最佳值为0;相对最大绝对误差表示符号为RMAE,最佳值为0。测定系数、均方根误差以及相对最大绝对误差计算公式如下:
式中:yi为第i个测试点的仿真值;为第i个测试点的近似值;为测试点仿真值的平均值;m为总样本的点数;k为测试的点数;S为标准差。
通过计算,Kriging模型与NPR模型构建的生产线机械臂近似模型的测定系数、均方根误差、相对最大绝对误差如表7 所示。
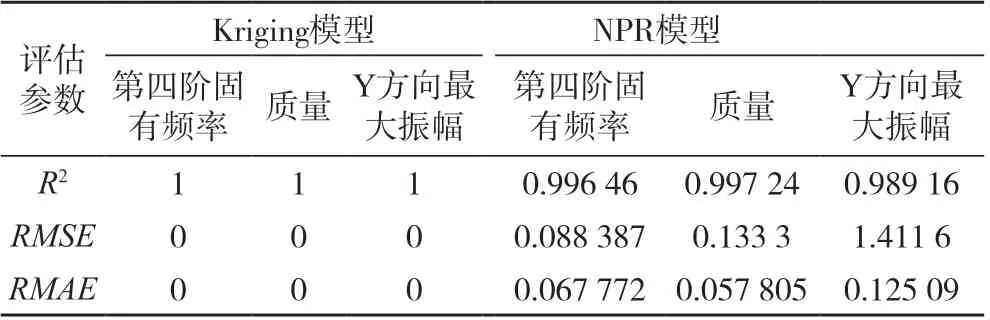
表7 Kriging模型与NPR模型对比Tab.7 Comparison between Kriging model and NPR model
由表7 可知,Kriging模型拟合精度高于NPR模型,尤其是NPR模型Y方向最大振幅的均方根误差偏离最佳值较远。因此,选择Kriging模型构建的近似模型。
5 结构优化
为方便分析,需要提前构建生产线机械臂设计变量与响应值之间的数学模型。将生产线机械臂设计变量作为变量,将生产线机械臂的第四阶固有频率P19以及质量P20作为约束,将Y方向最大振幅P39最小作为目标[24-29],构建好的数学模型为:
式中:Di为设计变量,Da为设计变量下限,Db为设计变量上限。
运用MOGA法进行求解优化,设置最初生成10 000个样本,每次迭代生成3 200个样本,并在最多20次迭代中找到3个候选样本,通过求解筛选出3个候选点,如表8所示。候选点1的优先级高于候选点2与候选点3,因此选取候选点1进行后续优化[30-34]。
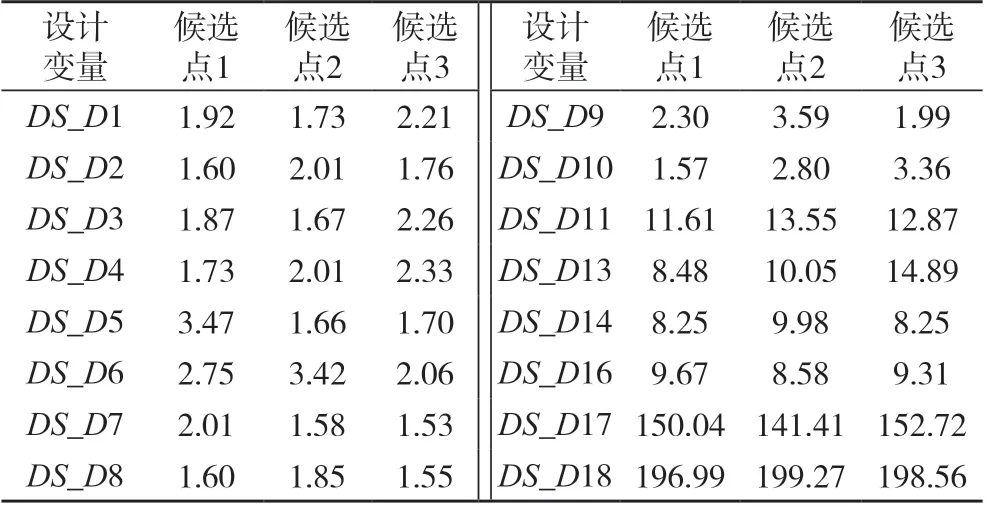
表8 候选点数值表Tab.8 Table of candidate point values
根据得到的候选点1,综合考虑生产线机械臂设计变量与响应值之间的关系,按照灵敏度正负关系,进行人工调整,最终得出满意的数值。生产线机械臂经过调整后的尺寸如表9所示。

表9 调整后的尺寸Tab.9 Adjusted dimensions
按照人工调整得到的数据,重新对生产线机械臂进行建模,并对其进行静态和动态性能分析,优化后的数据如表10所示。
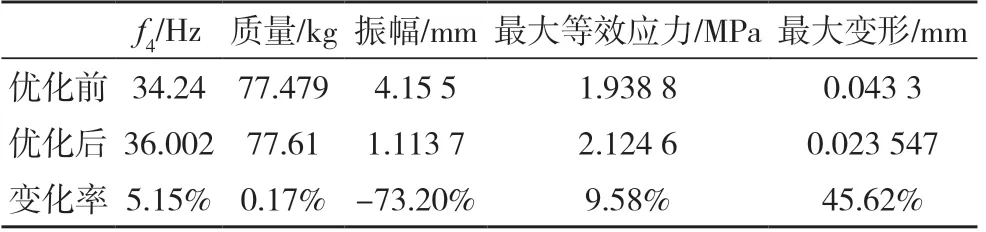
表10 调整后的模型参数Tab.10 Adjusted model parameters
将优化后生产线机械臂的动静性能与优化前生产线机械臂的动静性能进行对比,可以发现,优化后生产线机械臂的最大等效应力为2.124 6 MPa,低于其在受到约束情况时的最大等效应力163.33 MPa,满足静强度要求;最大变形为0.023 547 mm,低于生产线机械臂可以承受的最大静变形量0.194 mm,满足静刚度要求。此外,优化后生产线机械臂的第四阶模态固有频率提升了5.15%,并且T型板在Y方向的振幅降低了73.20%,满足生产线机械臂上下料过程中左右晃动幅度小于等于2 mm的要求。同时,优化后生产线机械臂的质量也没有显著增加。
6 结论
本文运用建模软件与有限元分析软件的协同仿真技术,研究了生产线机械臂的动静性能,通过Parameters Correlation模块分析生产线机械臂设计变量对整体质量、第四阶模态固有频率及Y方向最大振幅的灵敏度,筛选出对生产线机械臂影响较为明显的设计变量。
运用拉丁超立方抽样法得到筛选出的设计变量及对应输出的样本,通过Kriging模型与NPR模型分别构建生产线机械臂的近似模型,通过分析响应面及拟合精度得出,Kriging模型构建的近似模型优于NPR模型构建的近似模型。运用Kriging模型构建的近似模型对设计变量进行了优化,并对优化后的数据进行人工调整,再次建模并进行静态和动态性能分析,结果表明,优化后的生产线机械臂性能显著提高,且其晃动的幅度也满足上下料精度要求。
