基于IE及整数规划理论的家具生产线平衡优化
2024-04-02张仲凤张继娟
王 辉 张 蕾 张仲凤 张继娟
(1.中南林业科技大学,湖南 长沙 410004;2.国家林业和草原局绿色家具工程技术研究中心,湖南 长沙 410004;3.湖南省绿色家居工程技术研究中心,湖南长沙 410004;4.东阳市家具研究院,浙江 东阳 322100)
在全球化和信息技术迅速发展的背景下,制造企业间的竞争日益激烈,如何优化生产线已成为当前研究的热点[1–7]。自流水线生产诞生以来,国内外学者对生产线平衡问题开展了大量研究,并逐渐形成了以工业工程为基础的理论框架[8-10]。随着计算机技术的不断进步,智能优化算法、仿真软件等现代技术与传统IE方法相结合的方式不断出现,为现代生产线的平衡优化提供了新的研究方向[11-15]。
目前有关生产线平衡的研究多以制造业为主体,主要从理论构建和实际应用两方面进行探讨。相关研究情况如下:
1)采用单一方法优化生产线(定量或定性)。钱筱楠等[16-17]使用过价值流图法对板式定制家具生产过程进行优化。柴富容等[18]利用Witness对凸轮轴生产线进行仿真优化,大大降低了在制品数。赵晏林[19]采用启发式算法对家具生产线平衡进行优化求解。陈莎等[20-21]采用过遗传算法对生产线平衡进行改善。
2)多种方法组合优化生产线(定量+定性)。郭洪飞等[22]采用价值流图法优化焊装生产线,并利用Flexsim对改善效果仿真分析与评价。郭继东等[23-26]采用工业工程、数学模型法、仿真模拟法等方法的综合运用来优化生产线。总体来看,采用定性分析有主观意识过强的问题,而定量分析则可能缺乏数据的支持,多种方法优化生产线的效果更为显著。
基于此,本文以湖南某一定制家具企业为例,针对其木门扇生产线采用定性和定量相结合的方法进行优化,从而提高企业生产线平衡率和生产效率,达到降本增效的目的。
1 家具企业车间现状
1.1 企业简介
S企业是一家集设计研发、生产、销售于一体的实木定制家具企业,其生产模式主要是按订单生产。该企业由于生产设备老旧、工位划分不合理等原因,导致车间存在制品堆积、生产线不平衡等问题,生产能力难以满足订单需求。因此,需要对其现有生产线进行优化升级。
1.2 车间现状分析
以该企业产量最大的平板镶嵌门生产车间为例,其中门扇生产主要分为门芯板和门框两部分,整个生产过程共有16个工位(即16道工序)。木门扇生产线各工位对应作业元素及标准时间如表1所示。
1.3 生产线平衡分析
生产线平衡是一种通过分析生产线上各工序的负荷,调整各工序之间的负荷分布,使各个工序的产能实现平衡的技术手段[27]。依据上述测定数据,将门扇生产线各个工位的标准时间绘制成柱状图,如图1所示。其中,工位9是严重制约门扇生产线平衡的瓶颈工位。生产线的平衡指标计算如下:

图1 生产线各个工序作业时间分布Fig.1 Distribution of operation time for each process of the production line
生产线平衡率:
生产线平衡损失率:
生产线平滑指数:
式中:CT为生产线节拍,min;n为工序的数量,个;T总为作业总时间,min;Ti为第i个工序的作业时间,min。
由计算结果可知,S企业门扇生产线的平衡率不到60%,表明该生产线存在明显的不平衡现象,需要针对瓶颈采取措施来优化生产流程。
以S企业门扇车间生产流程为依据,建立仿真模型。由于车间工人采取单双休制,每天工作8 h,因此设定模拟一个月的车间生产过程,运行结束后的状态如图2所示。
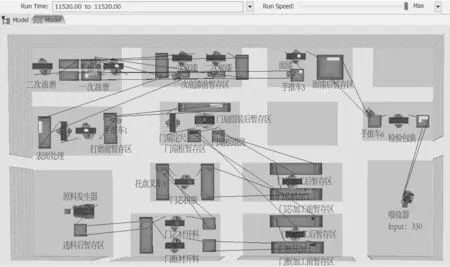
图2 门扇生产线模型运行结束状态图Fig.2 Door leaf production line model end of operation state diagram
2 基于IE方法的门扇生产线平衡优化
2.1 瓶颈工序改善
根据实地调研可知,该企业在整个实木门扇生产过程中,没有充分利用自身操作人员多能工的优势。因此,为有效提高整体的生产效率,拟重新规划工序的个人分工。根据门扇加工工艺及作业元素划分,绘制出木磨瓶颈工位的流程程序,如图3所示。根据木磨作业流程程序图,运用“5W1H”技术对木磨工位作业流程进行分析,如表2所示。

图3 木磨作业流程程序图(改善前)Fig.3 Wood milling work flow program diagram(before improvement)

表2 木磨瓶颈工位“5W1H”分析表Tab.2 Analysis table of "5W1H" of wood mill bottleneck station
在上述分析的基础上,运用“ECRS”原则对木磨工位进行重新合并和重排,简化加工步骤。改进后门扇木磨流程程序图如图4所示,其中所涉及的内容如下:

图4 木磨作业流程程序图(改善后)Fig.4 Wood milling work flow diagram (after improvement)
1)简化原则:作业人员操作不规范,门扇连接处打磨困难,故在门扇装配前对门芯板以及门扇框周边进行打磨,降低后续砂纸打磨难度。
2)合并原则:电动打磨机、气动打磨机、腻子粉等摆放位置分散,作业人员需多次寻找工具,故整理工作台后,将打磨工具放置到固定位置,方便作业人员一次性寻找。
3)重排原则:门扇搬运至木磨区后,先检查门扇表面,后放置在工作台上,以免门扇检查不合格,后续返工增加搬运。
4)取消原则:加强批灰用料规范及操作,操作员批灰完成后,门扇另一面已自动晾干,无需等待即可进行后续打磨。
相比于调整前木磨作业流程程序,删减了批灰晾干等待的过程,且整个加工次数减少到4次,搬运次数减少到3次,所用工时减少了5.36 min。另外,门扇组装工序调整后增加了一定的打磨作业,因此所用工时由14.06 min增加到15.06 min。
根据表3可知,改善后的木磨作业时间为24.5 min。然而,在整个生产线中,木磨工序仍旧是限制整体生产能力的瓶颈工序。因此,在改善木磨作业流程的基础上,增添一个相同的木磨工位。经过这一改进后,木磨工序不再是生产线的瓶颈,而工序4门芯拼板却成为新瓶颈。

表3 木磨作业优化前后对比Tab.3 Comparison before and after optimization of wood grinding operations
2.2 人机操作优化
门芯拼板划分为门芯材拼板和拼板后压刨两个作业元素,其中前者的好坏决定了后续压刨作业的难易程度。因此,门芯材拼板作业的优化是当前需要解决的关键问题。首先,了解门芯拼板作业的相关工作步骤,绘制出拼板作业人机分析图(图5)。然后,运用ECRS原则,在机器开始板材胶拼期间,通过对下一块门芯材进行组胚划线定宽、涂胶、检查平整度等操作,提高设备利用率至52.89%。最后,整理出改善后的人机作业分析图(图6)。
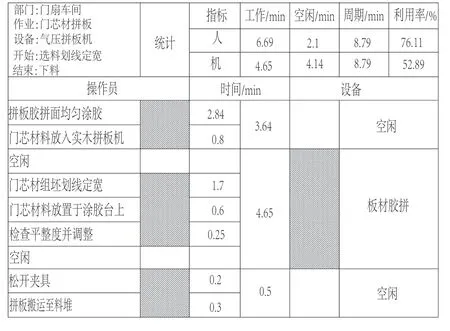
图6 拼板作业人机分析图(改善后)Fig.6 Puzzle operation man-machine analysis diagram(after improvement)
2.3 加工设备升级
在实木门的生产过程中,榫槽加工是一个非常关键的环节,其质量和精度对后续工序和最终产品的质量水平具有决定性的影响。S企业门扇框机加工使用的MX5117B立式铣床易产生噪音,且需要技术水平高的操作人员。实木门梃机能自动实现刀具更换,并通过智能控制系统自我调整和优化,有效提高了加工效率,实现了更加快速、精准和高效的加工效果。设备升级所更换的实木门梃机型号及参数如表4所示。

表4 实木门梃机型号及设备参数Tab.4 Solid wood door machine model and equipment parameters
根据考察得知,该款设备8 h大约能生产门扇框60套左右。应用于门扇生产线时,计算得出单件门扇框钻孔、立铣开槽加工时间约为8 min。
2.4 改善效果分析
基于以上IE方法对产线的局部改善,多个工序的作业元素划分情况以及作业时间发生改变,经重新测定计算得出情况如表5所示。从数据中可以看出,生产线平衡率从51.04%增加到71.41%,平滑指数也从15.65降低到6.51。此时,工序4门芯拼板再次成为整条产线的瓶颈,IE改善陷入了不断循环的困境。
3 基于0~1 整数规划的门扇生产线平衡优化
3.1 作业元素优先关系的确定
根据前文的作业元素重新划分以及增添的工位,绘制出门扇生产线作业优先关系图,如图7所示。其中,圈内数字表示作业编号、圈外数字表示作业加工时间、箭头表示作业的先后顺序。

图7 JZ-002 门扇装配网络图Fig.7 JZ-002 door leaf assembly network diagram
3.2 构建0~1 整数规划模型
为了更清晰地描述和解决生产线平衡优化问题,在建立0~1整数规划数学模型前需要定义以下符号及变量:
3.2.1 相关符号及含义
模型中的符号及含义如表6所示。

表6 模型中的符号及含义Tab.6 Conformity and conformance meaning in the model
3.2.2 决策变量
相应的0~1整数规划模型的具体约束条件如下:
1)门扇生产线上的每个作业元素必须分配到相应的工序上,且不能重复分配;
2)在门扇生产线中,如果作业元素S被分配到工序K上,则其紧前作业元素i只能被分配到1至K工序中;
3)门扇生产线中,各工序作业时间之和必须小于生产节拍。
建立的0~1整数规划模型如下:
目标函数:
约束条件:
3.3 LINGO软件求解
Lingo软件主要用于解决线性、非线性以及整数规划等各类运筹学问题,具有速度快、易于分析和求解大规模问题的最优解等优点[28–30]。在Lingo软件中输入相应的
表5 IE方法改善前后效果对比
Tab.5 Comparison of effects before and after IE
method improvement程序语言并运行,得到数学模型的求解报告,如图8所示。

图8 第Ⅱ类平衡问题的模型求解报告图Fig.8 Model solution report diagram for type II equilibrium problems
由图8可知,当工序数为16时,生产线最小生产节拍为18.64 min。整理各个作业元素被分配到工序的情况,如表7所示。
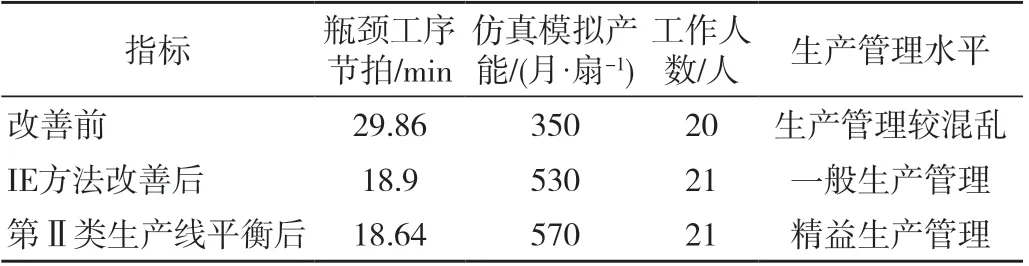
表8 其他指标对比Tab.8 Comparison of other indicators
4 门扇生产线优化效果分析与评价
4.1 基于Flexsim的仿真验证
为验证Lingo软件的求解结果,重新建立平衡优化后的仿真模型。根据表7中的数据设置Flexsim模型的相关参数,并按工艺流程对实体进行逻辑连接。建立并运行优化后的Flexsim仿真模型如图9所示。
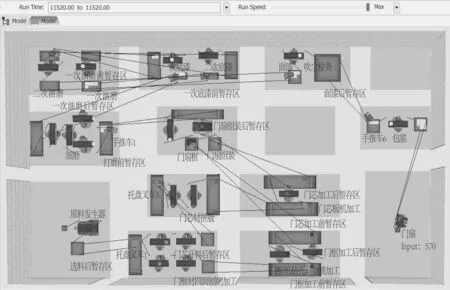
图9 平衡优化后的仿真模型Fig.9 Balanced and optimized simulation model
4.2 评价指标对比验证
由前文可知,通过IE方法对实木门扇生产线进行局部改善后,生产线平衡率虽有一定的提升,但改善效果仍达不到预期目标。因此,运用Lingo软件进行建模求解,以达到对整条生产线进行综合优化的目的。生产线平衡指标对比情况如图10 所示。

图10 生产线平衡指标对比图Fig.10 Comparison chart of production line balance indicators
对比生产线平衡前与平衡后的各类指标可以发现,生产线平衡率提高至84.73%,生产线平衡指数下降至3.35,仿真模拟产能由350 扇/月提升至570 扇/月,验证了优化方案的有效性。由于门扇车间的员工都能熟练掌握各种生产设备以及相关木工加工技术,因此作业元素再分配并不会对整体生产线的平稳运行造成太大的影响。
5 结论
为解决门扇生产线不平衡问题,本文提出了IE方法与整数规划理论相结合的生产线平衡优化方案。在改善局部工序以及升级门扇加工设备的基础上,应用整数规划理论对生产线作业元素进行重组,实现了生产线平衡的再优化,并通过对比生产线平衡指标和Flexsim仿真模拟,进一步验证了该方案的有效性。结果表明,基于IE和0~1整数规划数学模型能够很好地解决家具生产线问题,可为实木定制家具生产线优化与生产线平衡率提升提供参考和新思路。
