舰用雷达阵面在不同冲击环境下的响应分析

周世新,杨 斌

(南京电子技术研究所, 江苏 南京 210039)

0 引 言

舰用设备的抗冲击性能是舰船生命力和战斗力重要保证,为了提高舰用设备的抗冲击能力,分析设备在不同冲击环境下的响应十分必要。现阶段相关研究人员通过动力设计分析方法( DDAM) 或时域动态分析方法开展了舰用设备的抗冲击响应分析和抗冲击设计等研究[1-2],作为舰用设备重要组成的电子设备的研究内容主要集中在冲击载荷作用下响应的数值仿真分析[3-5],却缺少关于不同冲击环境下舰用电子设备的相应分析。

本文进行研究的基础方法是相关专家和学者已经完成的关于舰用电子设备冲击响应的方法,在不同的冲击环境下来分析舰用雷达阵面的响应,并进行数值仿真,探究冲击谱参数的变化对舰用电子设备响应的影响。

1 舰用电子设备抗冲击要求

舰用电子设备的抗冲击性能是舰用电子设备环境适应性的重要指标,在抗冲击设计当中,设备承受冲击强度的定义方法与标准是最关键的内容,与我国相比,西方海军强国的舰船设备抗冲击标准就是建立在大量的实船爆炸试验的基础上。现阶段,我国就是参照美国的相关标准来制定我国现有标准的,GJB150.18和GJB1060.1-91均属于这种情况,美国设备也作为仿制对象影响了我国轻型及中型等冲击机发展[6]。

国军标GJB50.18中冲击试验的冲击输入量值无量化概念,只规定轻型设备(200 kg以下)沿设备三根主轴方向按三种固定锤高,总共进行9次冲击;中型设备(2.7 t ,1t=1 000 kg)以下分三组不同锤高和砧板行程,每组分别为水平和倾斜安装,进行6次冲击;重量级设备(2.7 t～13.4 t)经受5次水下爆炸冲击,TNT当量为27kg(距离为18m、12m、9m、7.5m、6 m), 按照工况进行试验,若设备不发生损坏则考核合格。

德国BV043 /85 抗冲击标准详细给出了全船共三类安装区域的冲击谱(表1)[6],适合于产品设计阶段的仿真分析。

表1 BV043/85规范中的冲击谱Tab. 1 Shock spectrum in BV043/85 specifications

注:Ⅰ类安装区域指船壳基座和主甲板以下隔舱壁;Ⅱ类安装区域指下甲板和主甲板隔壁;Ⅲ类安装区域指上层建筑。

2 理论计算分析

在结构力学当中,作为基础激励系统的凝聚思想可以用有限个自由度来取代多个自由度系统[7]。舰用雷达阵面由不同的子阵组成[8],如图1所示,主要由子阵和阵面骨架等组成,各子阵之间相互独立,各自安装在阵面骨架上,可以通过图2来表示天线阵面。舰用设备主要受到垂向的冲击载荷,各子阵通过阵面骨架受到冲击载荷作用,因此在已有研究成果[9-10]的基础上,通过单自由度系统来简化每个子结构,完成基础激励的多自由度系统数学模型建立。如图2所示,通过对冲击谱量值的变化求解各个子结构的响应来分析不同冲击环境对舰用雷达阵面冲击响应的影响。

图1 舰用雷达阵面模型Fig.1 Rigid mounted antenna array model of ship-borne radar

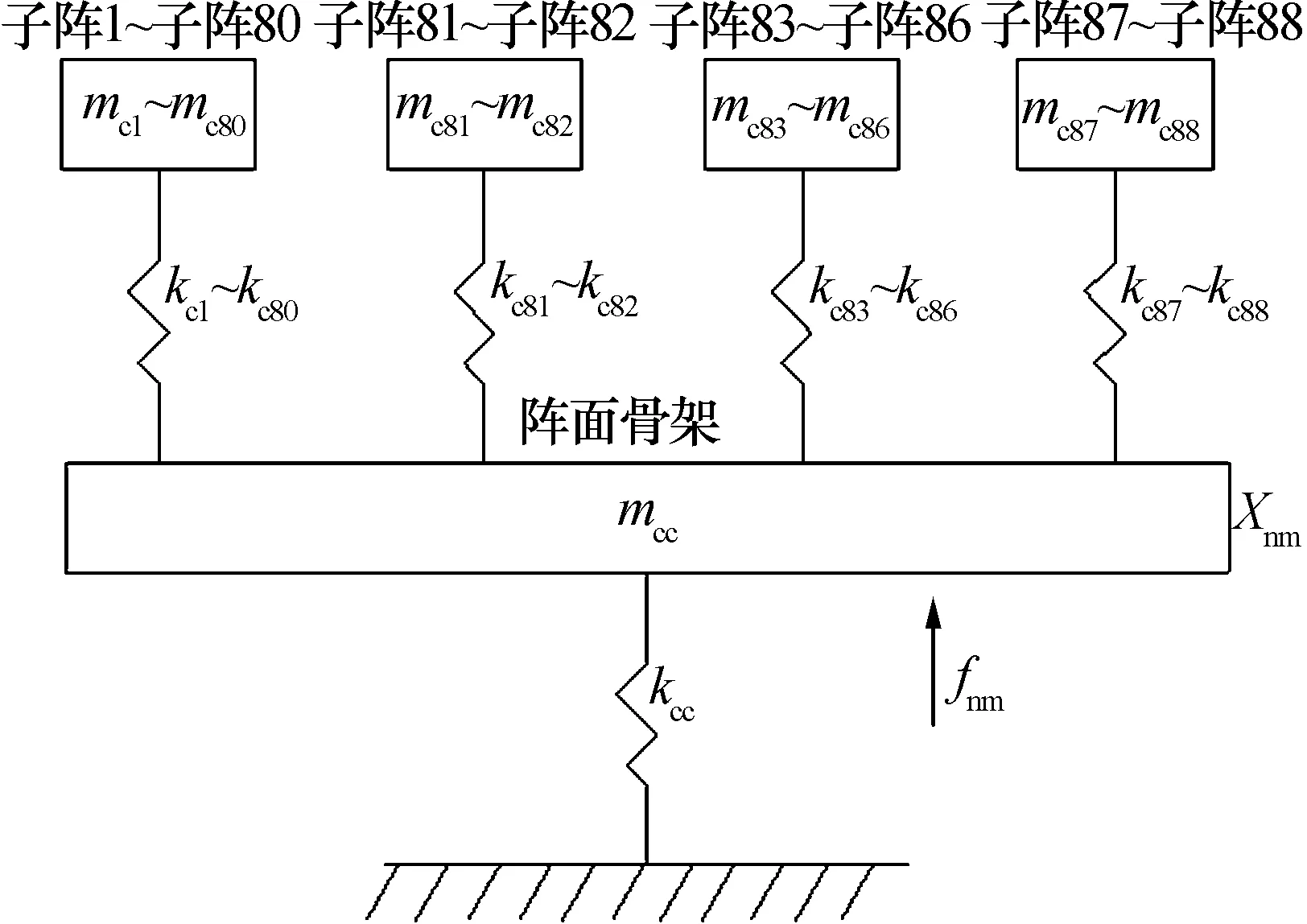
图2 基础激励多自由度系统Fig.2 Basic incentive multi-degree-of-freedom system

某舰用雷达阵面的89个自由度系统由阵面骨架和88个子阵组成,子模型的质量与子结构的重量保持一致,子模型的弹簧刚度系数可通过子结构自由态下的一阶固有频率进行确定,相应的模型数据及参数也能够通过计算完成,如表2 所示。图2 中各子模型的质量与弹簧刚度系数也是由此得到的。在不同的激励力的作用下,能够解出如图2所示的多自由度系统的值,也就能够通过模拟分析来判断舰用雷达阵面的响应。

表2 舰用雷达阵面有限元模型各模型参数Tab.2 Finite element model parameters of ship radar array

频域表示的冲击输入冲击谱(表1)可按德国BV043/85 规范提供的方法转换为时域表示的冲击谱,如图3所示,以下是各参数计算公式。

图3 时域冲击谱Fig.3 Time-domain shock spectrum

(1)

式中:A0代表表1中的等加速度谱值;D0代表表1中的等位移谱值;V0代表表1中的等速度谱值;a1为转换后的正向时域加速度峰值;a2为转换后的反向时域加速度峰值;t2为对应转换后的正向加速度峰值发生时刻;t3为转换后加速度为0并由正转负的发生时刻;t4为对应转换后的反向加速度峰值发生时刻;t5为转换后的时域加速度波形结束时刻。

图3中实线(─)代表BV043/85 抗冲击标准中规定的Ⅲ类安装区域冲击谱,虚线(┅)表示Ⅲ类安装区域冲击谱的谱加速度由100 g增加为170 g其余不变的加速度时间历程,点虚线(…)表示Ⅲ类安装区域冲击谱的谱速度由5 m/s增加为6 m/s 其余不变的加速度时间历程,点划线(-·-·-·)表示Ⅲ类安装区域冲击谱的谱位移由5.2 cm减少为4.2 cm 其余不变的加速度时间历程。如图3所示,改变谱加速度主要改变时域双三角波的正波幅值,改变谱速度和谱位移主要改变时域双三角波的负波幅值和冲击脉宽。

利用时域表示的冲击谱来表示频域表示的冲击谱后,表示方法见以下分段函数。

(2)

式(2) 表示加速度是非简谐的激振力,由于傅里叶级数是将时域数据分解为无穷多个离散的谐波,用傅里叶级数来表示式(2),表示n个简谐激振力之和,谐波频率为ωn,n为谐波次数。在[0,t5]中的a(t)作为一个函数是有定义的,为了满足狄利克雷条件进行偶延拓或奇延拓,a(t)就可展开为傅里叶级数的和函数,表示为

(3)

式中:τ=t5;a0为0时刻的加速度值。

(4)

当t=0 时,由式(2) 得a(0)=0,用复数形式来表示加速度可以使运算更加简便,用复数的实部来表示式(3)为

(5)

用a(n,t)=Re(aneinω0t)来表示频率为nω0的简谐激励当中傅里叶级数第n项,x(n,t)=Re(aneinω0t)用来表示位移x,对不同激励频率nω0计算得到的结构位移响应进行求和,得到动力响应,即

(6)

采用结构动力学问题求解方法来解决结构位移x的相关问题,对边界模态进行虚拟约束[11],将舰用雷达阵面骨架及阵面内部结构分布定义为选定边界及非选定边界,两者的自由度的集合分别定义为m集、s集,以下矩阵表示s=88,m=1的89个自由度系统。

(7)

式中:M为系统的质量矩阵,K为系统的刚度矩阵。

根据边界和内部自由度的定义,设备系统的运动方程可写为

(8)

式中:x为位移矩阵;f为外力向量矩阵;下标n为谐波次数;下标m为选定边界自由度;下标s为非选定边界自由度。

Λb表示虚拟约束边界的特征值是通过式(8) 的质量和刚度矩阵求解得到,特征向量Φb的求解方法相同。虚拟约束界面模态的正交关系为

(9)

对于简谐激励f=f0eiωt,位移幅值Xn的控制方程为

(10)

令λ=ω2,可得

(Kss-λMss)Xns+(Ksm-λMsm)Xnm=fns

(11)

因而,S集位移幅值Xns和整体位移幅值Xn都可以借助m集位移幅值表示如下

Xn=TcXnm

(12)

其中

Tc=Φc0+λHbμb

可得

Xb=Φc0Xnm+φbqnb

(13)

由于作用于系统内部自由度的作用力等于零,即fns等于0,则可得

(14)

只考虑阵面骨架的加速度输入,则fnm=mcca,可得

(15)

则最终可求得整个系统的位移幅值如下所示

(16)

最后求出与各个激励力频率nω0对应的舰用雷达阵面整体响应Xn,通过式( 6) 得到舰用雷达阵面总的动力响应。

按照本文中的方法,计算得到图3实线所示的冲击谱、只增加加速度值的虚线所示的冲击谱、只增加速度值的点虚线所示的冲击谱、只增加(减少)位移值的点划线所示的冲击谱分别作用下,阵面各子结构的位移响应幅值,见表3。

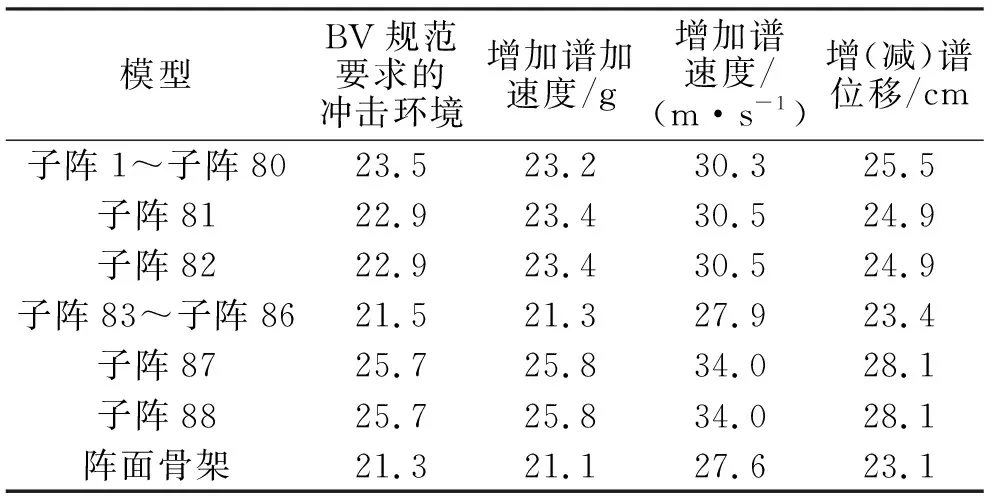
表3 不同冲击环境下雷达阵面位移响应幅值Tab.3 Radar array displacement response amplitude under different impact environments mm

根据表3 的数据显示,结合图4的位移响应时间历程曲线能够得到以下结论:各子结构的响应几乎没有随着高频段的谱加速度在冲击谱中的大幅增加而发生变化。中频段的谱速度和低频段的谱位移分别稍微变化(谱速度由5 m/s增加至6 m/s,增加20%,谱位移由5.2 cm减少至4.2cm,减少19%),各子结构的位移响应幅值就有较大变化(增幅分别为32.3%,9.3%),两者对系统的响应影响较大。

图4 不同冲击环境下雷达阵面位移响应时间历程曲线Fig.4 Time history curve of radar array displacement response under different impact environments

3 冲击响应仿真分析

以某舰用雷达阵面为分析模型,如图1。用频域表示的BV043/85抗冲击标准规定的Ⅲ类安装区域的冲击环境进行仿真计算,如图5中的实线所示,并在此基础上改变冲击谱中的加速度、速度、位移,分析设备的响应受到谱参数变化的影响程度。

图5 不同冲击环境的冲击谱Fig.5 Impact spectra of different impact environments

将BV043/85规范要求的冲击谱(如图5的实线(─)所示)作用于阵面的骨架,采用Ansys仿真软件得到阵面的Mises 应力云图,如图6所示。为了能够对阵面响应在不同冲击谱下的变化情况进行分析,以BV043规范为标准对冲击谱进行调整,冲击谱中高频段的谱加速度由100 g增加为170 g(增加70%),其余不变,如图5中的虚线(┅)所示,这两种冲击谱作用下的最大应力分别为99 MPa 和101 MPa,相差2%,因此谱加速度的变化对阵面响应影响可以忽略不计。

图6 BV要求冲击环境下的舰用雷达阵面响应Fig.6 Shipboard radar response under impact environment required by BV

改变谱参数,结合BV/85 规范要求对谱速度、谱位移进行调整。将BV043/85 规范要求的冲击谱的谱速度由5 m/s增加至6 m/s(增加20%),如图5的点虚线( … );谱位移由5.2 cm减少至4.2cm(减少19%),如图5的点划线(-·-·-· ),对阵面骨架分别加载不同的冲击环境,计算得到最大应力分别为127 MPa 和106 MPa,如表4所示。与谱加速度增加的情况相比,冲击谱中低频段的谱位移和中频段的谱速度对阵面的响应有较大影响。

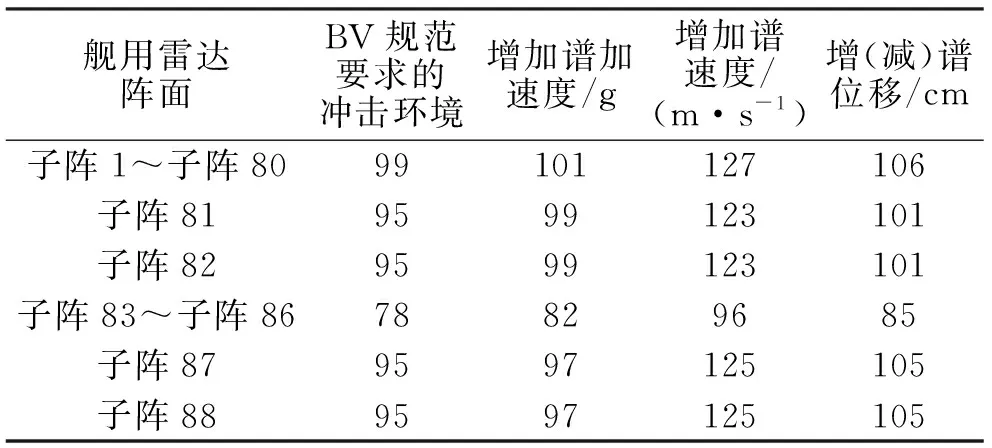
表4 不同冲击环境下的仿真结果对比(最大miss应力/MPa)Tab.4 Comparison of simulation results under different impact enviroments(Maximum Miss stress/Mpa)

数值仿真与理论计算得到的现象是一致的,也验证了本文理论计算模型分析不同冲击环境下舰用雷达阵面响应的正确性。

4 结束语

本文通过理论计算和仿真分析的方法求解舰用雷达阵面在不同冲击环境下的响应,提出了在不同冲击环境下,舰用雷达阵面冲击响应规律,根据结果显示:舰用雷达阵面响应受冲击谱中的谱位移、谱速度变化的影响较大,而对谱加速度大幅变化不敏感。本文方法可指导雷达抗冲击设计和评估。与此同时,针对谱位移减少,而时域双三角波中负波幅值反而增大的内在机理还需进一步研究。