基于极大似然的联合多传感器配准与融合

2024-04-01周学平谢依妨

现代雷达 2024年1期

周学平,谢依妨

(1. 中国电子科技集团公司第二十八研究所, 江苏南京 210007)(2. 广西贵港市港北区科技局, 广西贵港 537100)

0 引言

在多传感器多目标跟踪系统中,融合中心利用信息融合技术处理来自各传感器的量测数据,具有降低虚警率、增大数据覆盖面、提高目标跟踪能力以及增强系统故障容错性与鲁棒性等优点[1]。传感器配准和传感器数据融合是多传感器多目标跟踪系统中两个重要内容,传感器配准是为了消除传感器的系统偏差,从而提高系统对目标的跟踪精度[2],传感器数据融合指利用多个传感器数据集合中所包含的有用信息对估计目标的状态进行最佳估计[3]。多传感器融合的精度一定程度上与传感器固有系统误差相关,因此,对多传感器配准与融合进行联合研究具有迫切的工程需求以及重要的现实意义。

目前,传感器配准方法主要包括序贯处理方法和批处理方法。序贯处理方法主要是基于卡尔曼滤波、扩展卡尔曼滤波、无味滤波等实时估计方法[4-7],其将系统偏差作为待估计的状态量进行滤波估计求解,其计算量较小,可以进行实时计算,但不一定可以快速收敛。批处理配准方法主要包括实施质量控制法(RTQC)、最小二乘法(LS)、广义最小二乘法[2](GLS)、极大似然法[8-9](ML)以及精确极大似然法[10](EML)等,该类算法通过对一时间段内的数据进行集中处理,求取本段时间内传感器偏差的最优估计,其计算量随着数据的增长而变大。

多传感器融合分为集中式融合和分布式融合,本文研究的是集中式融合,其方法通常可分为并行滤波和序贯滤波,但此类方法通常是在传感器无系统偏差条件下进行的,传感器存在系统偏差时,其融合精度通常较差。

因此,当在多传感器带系统偏差的场景下进行融合处理时,需要联合进行多传感器配准和融合。本文通过引入基于量测函数的极大似然法,进行公式推导,同时对多传感器偏差和融合进行估计。仿真结果验证了该算法的有效性,并且具有较高的估计精度。

1 系统模型

考虑二维坐标下N个传感器对M个目标进行融合跟踪的场景,每个传感器的位置假设已知,带偏差量测模型为

zi(k)=h(xi(k))+η+w(k),i=1,2,…,M

(1)

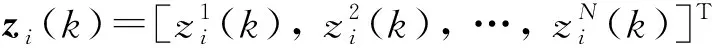
2 理论推导

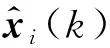
(2)

假设各传感器之间的量测噪声相互独立,为表示方便,在k时刻对于目标i,可得似然函数为

(3)

(4)

(5)

其中

Hi=[xhj(x)T]T=

(6)

式中:Hi为hi(·)在x处的雅可比矩阵。此时似然函数(3)在目标状态空间下近似为

(7)

使用矩阵运算公式

xTAx-2xTB+BTA-1B=(x-A-1B)A(x-A-1B)

(8)

式中:A为对称矩阵;x和B均为一般矩阵。利用上述公式 ,式(7)可重写为

(9)

其中

(10)

式(9)中的第二项可重写为

(11)

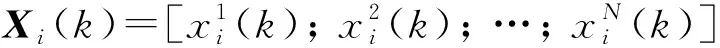
(12)

式中:block-diag表示为括号内各方块矩阵组成的块对角矩阵;[·]nm表示N×N矩阵中的子矩阵[11],其中n,m=1,2,…,N。

(13)

式中:K=1/|2πφi|1/2是归一化常量。

(14)

式中:上标-L表示矩阵Hj的左逆。对于多传感器系统,有

(15)

式(15)可写为更简洁的方程为

(16)

其中

(17)

(18)

在M个目标在采样时刻的所有量测下,系统偏差的最大似然估计为

(19)

通过式(8)、式(13)、式(16)和式(19),可得

(20)

通过矩阵运算式(9),式(20)可重写为

(21)

其中

具体的诉讼程序与普通民事诉讼相同，此处不再赘述。但需要提示的是，具体管辖法院可以参照《最高人民法院关于专利侵权纠纷案件地域管辖问题的通知》以及地方关于专利侵权管辖的具体规定确定。

(22)

3 算法流程

步骤1 在初始采样时刻k+1,初始化传感器系统偏差估计值η0为零。

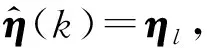
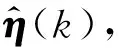
算法流程如图1所示。

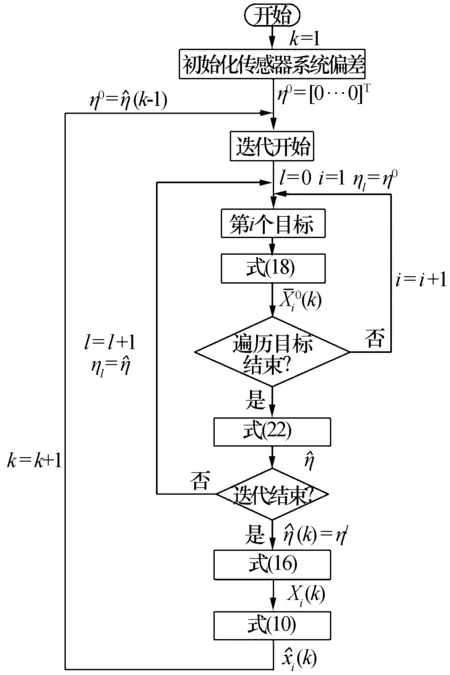
图1 算法流程Fig.1 Algorithm flow

4 仿真分析

在二维平面下,三个雷达对50个目标进行探测,三个雷达的坐标分别为雷达1位置ζ1=(0,0),雷达2位置ζ2=(0,100 km),雷达ζ3=(100 km, 0),雷达1系统偏差为Δρ1=400 m,Δθ1=-0.5°,雷达2系统偏差为Δρ2=500m,Δθ2=0.4°,雷达3系统偏差为Δρ3=-300 m,Δθ3=0.5°,量测噪声标准差均为σr=50m,σθ=0.05°。目标初始位置在[0, 200 km]×[0, 200 km]的区域范围内均匀分布且存在多种运动模型,雷达的采样周期为1 s,进行100次采样,仿真场景如图2所示。

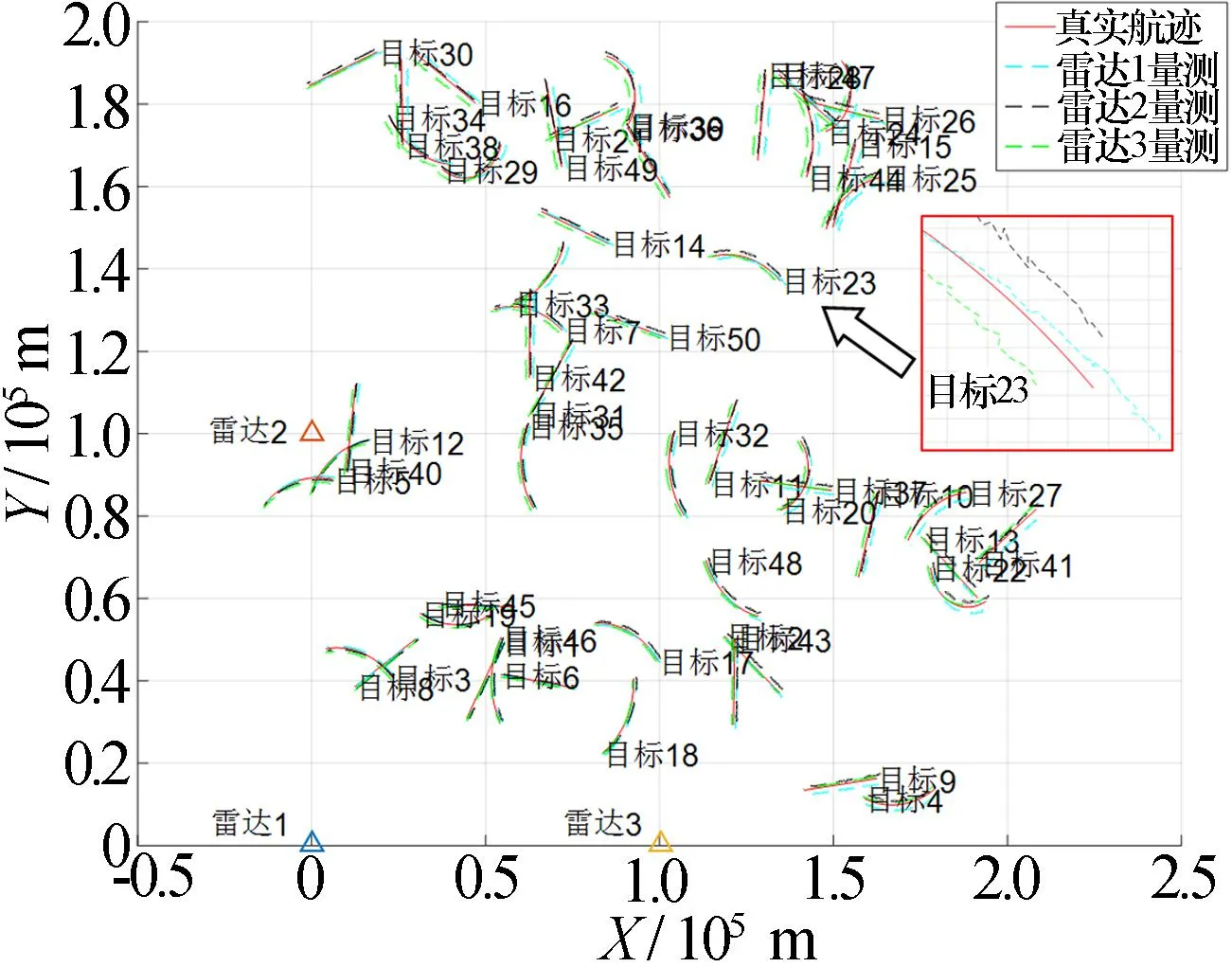
图2 仿真场景Fig.2 Simulation scene

图3、图4为雷达系统偏差真值与估计值对比图,图5、图6为配准前后距离量测和角度量测与真值对比图。从图3和图4可以看出,随着采样时间的进行,雷达系统误差估计值迅速向真值收敛。从图5和图6可以看出,配准后的量测值与真值几乎一致,体现了本文算法对雷达的系统误差估计具有快速的收敛性和较高的估计精度。

图3 距离偏差真值与估计值对比Fig.3 Comparison between true value and estimated value of distance devation

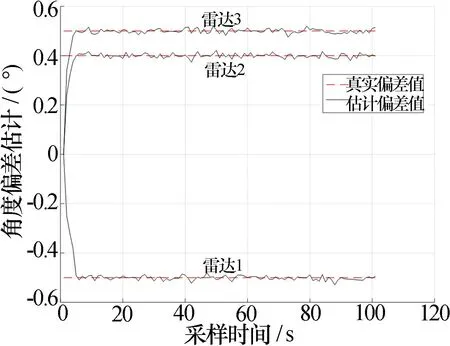
图4 角度偏差真值与估计值对比Fig.4 Comparison between ture value and extimated value of angular deviation

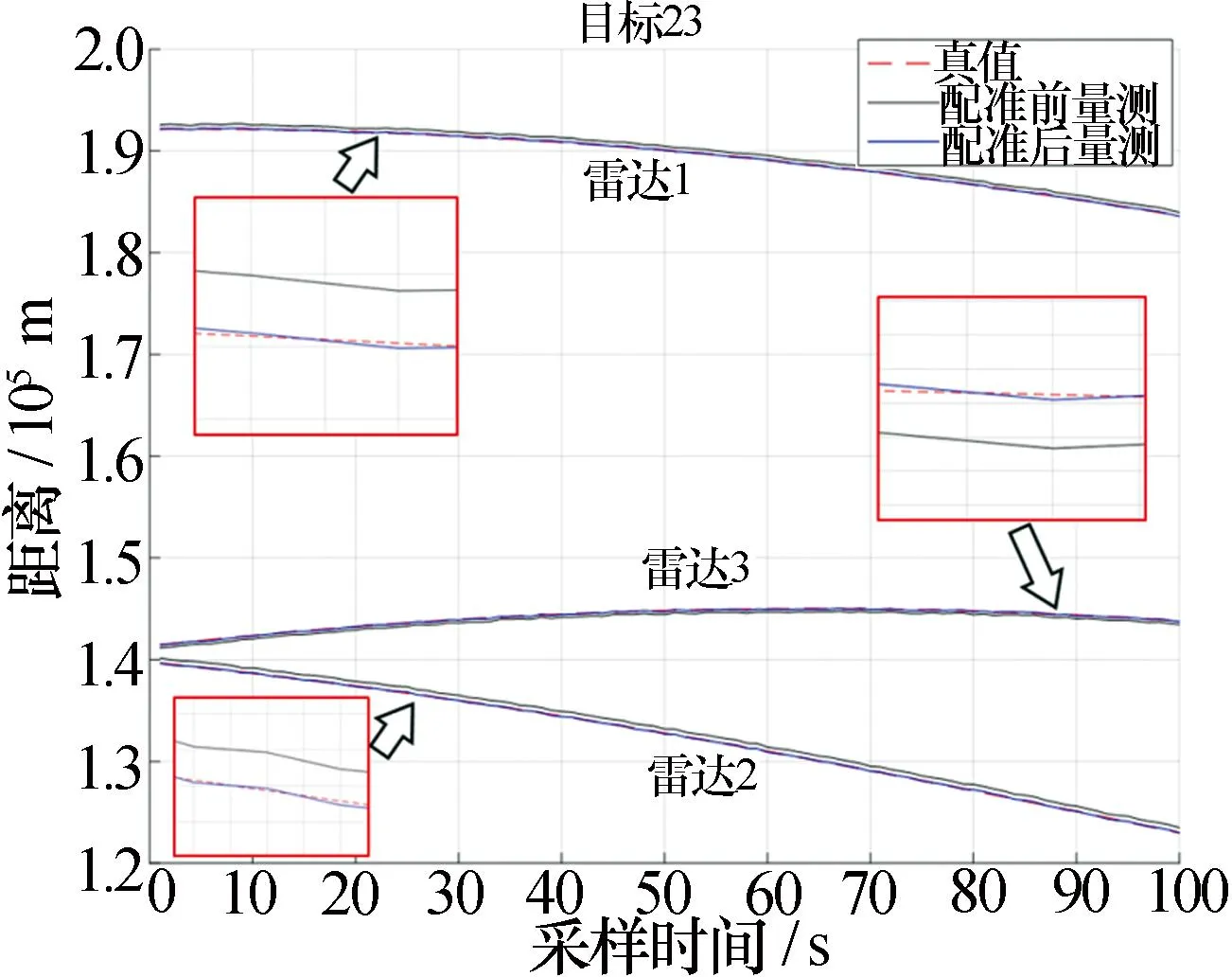
图5 配准前后距离与真值对比Fig.5 Comparison of distance to ture value before and after registration

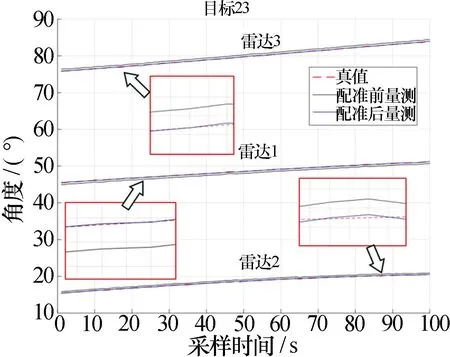
图6 配准前后角度与真值对比Fig.6 Comparison of angular to true value before and after registration

选取某一目标进行分析,图7为雷达原始量测、目标航迹真值和融合航迹的对比图,图8为各雷达原始量测误差与融合航迹误差的对比图,表1雷达原始量测误差值与融合航迹误差值的统计数据。从图表中可以看出,进行误差配准与融合后,目标位置误差从量测的千米量级下降到融合后的十米量级,大大提升了对目标的跟踪精度,表明了本文算法的有效性。