基于压缩感知的被动雷达导引头信源数估计方法
2024-04-01李槟槟时满红赵宏涛
王 资,李槟槟,时满红,赵宏涛,江 平
(空军预警学院, 湖北 武汉 430019)
0 引 言
被动雷达导引头搭载于反辐射导弹或反辐射无人机上,以雷达辐射的电磁波为制导信息,导引载体命中目标雷达。随着雷达反摧毁技术的发展,在雷达附近设置有源诱饵,利用传统被动雷达导引头采用比幅法或相位干涉仪法只能对单个目标进行测向和跟踪,且分辨角较大的缺陷,诱偏反辐射武器,使其失效[1]。因此,被动雷达导引头需要对多个目标进行分辨与测向,可采用阵列超分辨测向技术——空间谱估计测向[2]。但经典的空间谱超分辨算法,需要多快拍采样积累数据量使协方差矩阵满足统计特性,而被动雷达导引头所处的高机动平台,对测向实时性要求高,多快拍累积不现实[3]。另一方面,为更好地保护雷达,诱饵和雷达信号采用相参技术,但时序设置不一致且不规律,形成了不完全重合信号[4],若多快拍采样极易导致采样区间内信号非平稳,致使测向困难。因此,单快拍测向很有必要。
目前,单快拍测向方法的研究主要集中在空间平滑类算法[5]、伪协方差矩阵重构算法[6]、压缩感知算法[7]等。这些算法均假设信源数已知,而实际中,信源数往往未知,若信源数估计不准,测向算法会失效。
因此,准确估计信源数是测向的前提。关于信源数的估计,早期的方法是求出接收数据协方差矩阵的特征值,通过假设检验估算出信号子空间对应的较大特征值的个数,但“较大”的判断带有很强的主观性。经典的方法是基于信息论准则,如AIC准则[8]、最小描述长度(MDL)准则[9]等估计特征值个数,避免了假设检验的弊端;盖氏圆(GDE)方法[10]则依据盖氏圆盘定理将信号盖氏圆和噪声盖氏圆分离开,无需知道具体特征值数值就能估计信源数,可适用于色噪声环境。但这些方法都是基于子空间,需要多快拍采样,在单快拍的情况下估计性能大幅下降甚至失效。
针对单快拍估计的技术难题,可以借鉴近年来在图像处理领域提出的压缩感知理论[11],其能利用少量的压缩测量数据进行信号的重构,具备单快拍采样的潜力。文献[12]中,建立了压缩感知与阵列信号处理的联系。基于此,一些学者研究了在压缩感知理论框架下的信源数估计问题。文献[13]基于压缩感知稀疏重构的正交匹配跟踪算法,提出了一种变步长搜索的信源数估计方法,运算量较小,实时性较高,但在单快拍下性能欠佳。文献[14]基于压缩感知稀疏重构的基追踪算法,提出了l1稀疏正则化的估计算法,能在少快拍下精确估计信源数,但采用凸优化求解,运算量较大,实时性难以保证。文献[15]基于压缩感知稀疏重构的稀疏度自适应匹配追踪算法进行改进,设置迭代终止条件,但残差阈值的设定存在主观性。
为解决上述问题,本文结合被动雷达导引头的测向任务及对抗场景,研究基于压缩感知的单快拍信源数估计方法。将子空间类算法与压缩感知算法相结合,提出了一种改进的正交匹配跟踪算法,推导残差的变化规律,并构造目标函数估计信源数。本文方法在单快拍、少阵元、相干信号的条件下具有良好的性能。
1 阵列测向模型
考虑到被动雷达导引头对目标雷达进行定位,需要方位、俯仰二维测向,可采用图1所示的十字型阵列天线。该阵列位于X-Y平面,由分别位于X轴和Y轴的均匀线阵垂直交叉构成。位于X轴的阵元个数为M1+M2+1,位于Y轴的阵元个数为N1+N2+1。第j个信源Sj入射到天线阵的方位角为θj、俯仰角为φj。其中,方位角表示入射信号在X-Z平面的投影与X轴的夹角,俯仰角表示入射信号与X-Z平面的夹角。
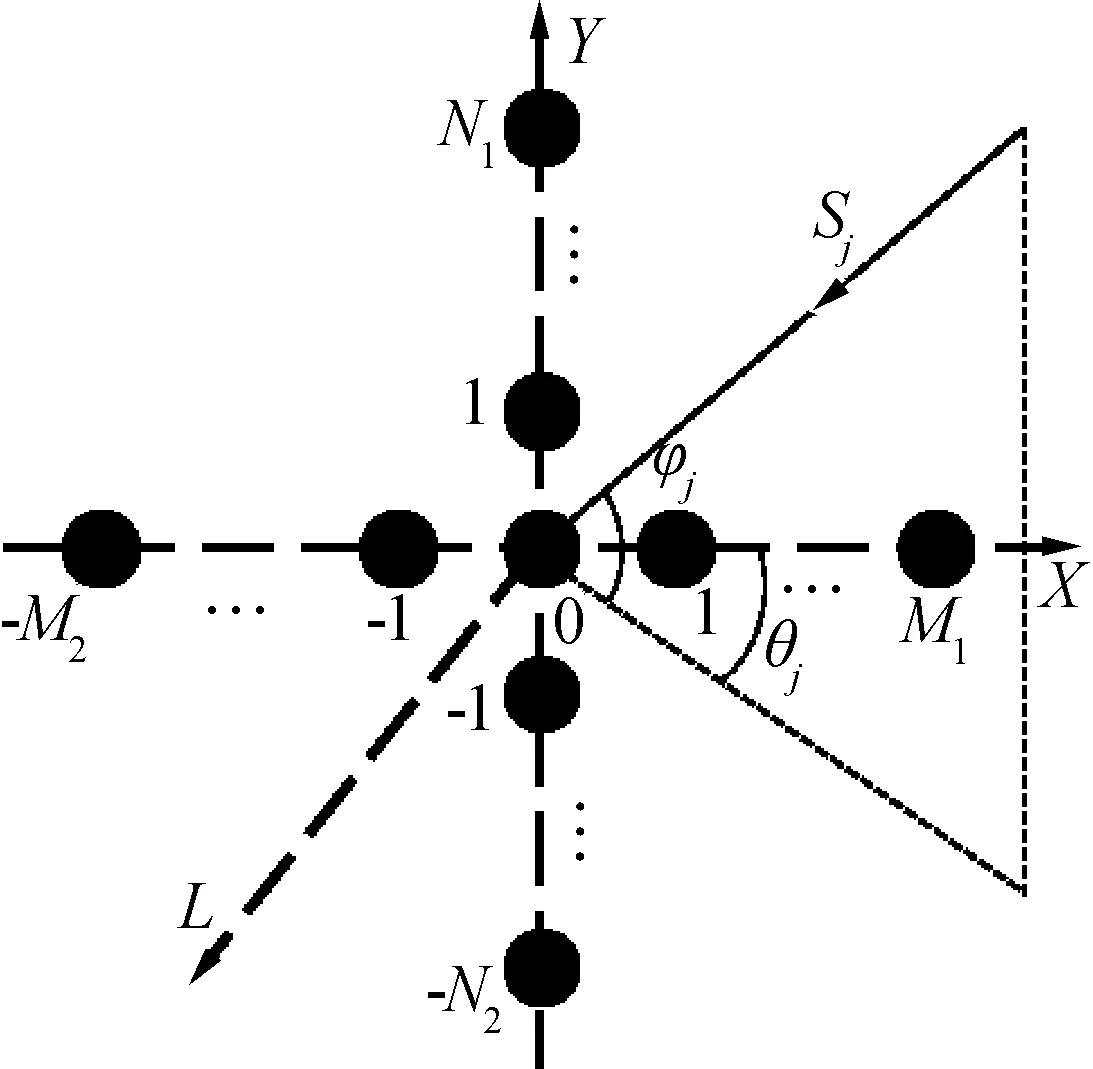
图1 阵列天线测向模型Fig.1 Spatial direction finding model for array antennas
按照先X轴阵元接收信号后Y轴阵元接收信号排列,则整个阵列接收信号可以表示为
r(t)=[X-M2(t),…,X0(t),…,XM1(t),
Y-N2(t),…,Y0(t),…,YN1(t)]T=
AS(t)+N(t)
(1)
式中:S(t)=[s1(t),s2(t),…,sp(t)]T,为p个入射信号向量;N(t)为噪声向量;A为阵列流型矩阵,可表示为
A=[α(θ1φ1),α(θ2,φ2),…,α(θp,φp)]
(2)
式中:α(θj,φj)为导向矢量,可表示为
α(θj,φj)=[Xα-M2(θj,φj),…,XαM1(θj,φj),
Yα-N2(θj,φj),…,YαN1(θj,φj)]T
(3)
以0号阵元为参考,X轴和Y轴上第i个阵元的坐标分别为(xi,0,0)和(0,yi,0),它们与参考阵元的波程差分别为
(4)
式中:c为电磁波传播速度。因此,式(3)中各元素可表示为
(5)
式中:ω为入射信号的角频率。由此,建立起了X轴和Y轴各阵元接收信号与各阵元位置坐标以及各信源入射的方位角、俯仰角之间的关系。
2 基于压缩感知的信源数估计方法
2.1 压缩感知基本理论
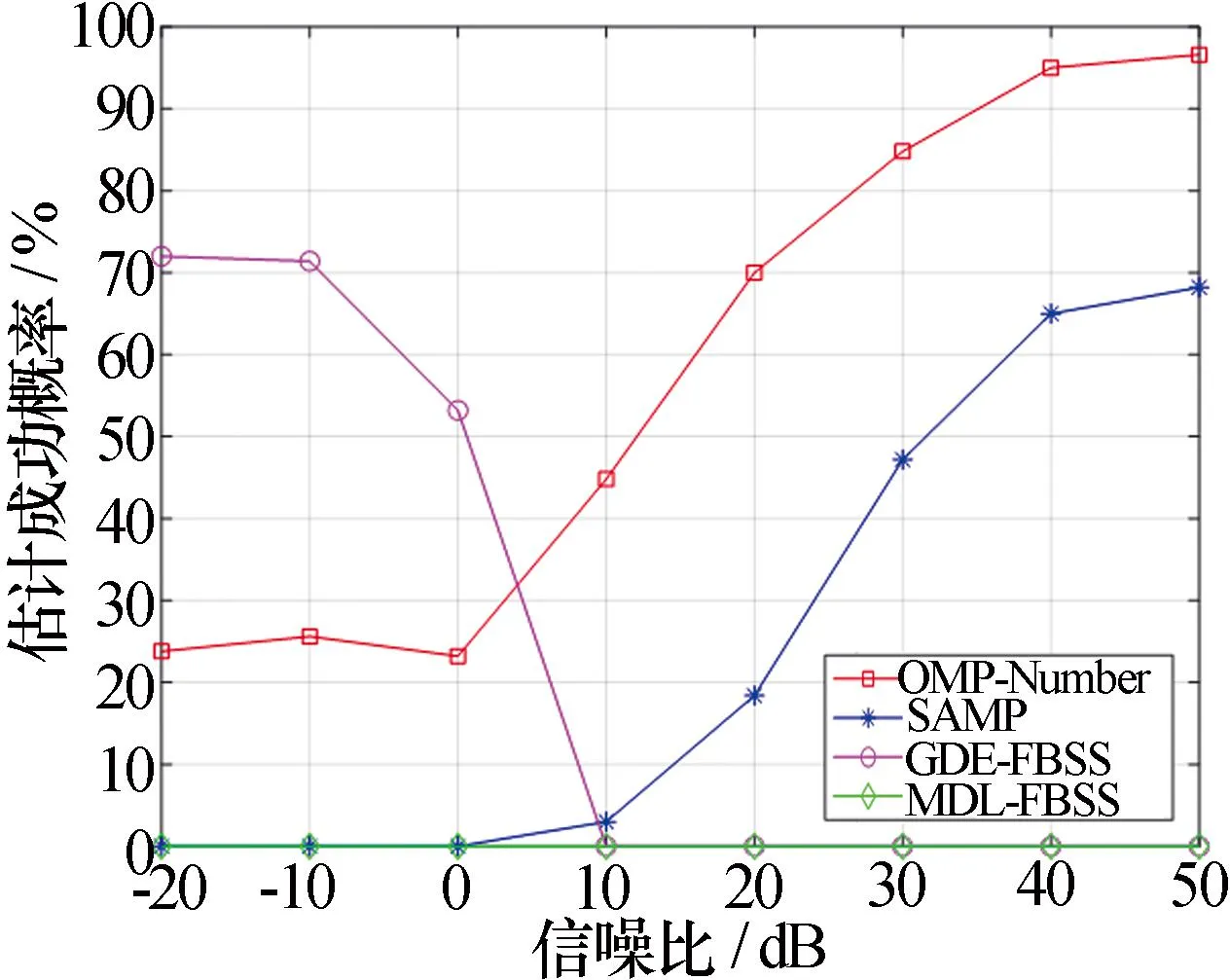
压缩感知理论表明:当原始信号具有可压缩性或稀疏性时,通过少量采样数据就可以精确重构出原始信号[11]。若原始信号本身不具有稀疏性,可通过变换具备稀疏性。设原始信号x=[x1,x2,…,xn]T可用n×n维稀疏基矩阵ψ=[ψ1,ψ2,…,ψn]进行线性表示,即x=ψs,其中s是一个具有稀疏度为k(k< y=φx=φψs=Φs (6) 式中:Φ=φψ为m×p维感知矩阵。如果Φ满足有限等距性质[11]等稀疏重构条件,就可以由采样信号y和感知矩阵Φ以极高的概率重构出稀疏信号s。s的稀疏重构即求解l0范数约束优化问题。 (7) 再由x=ψs即可恢复出原始信号x,实现了低维的采样信号重构出高维的原始信号。 压缩感知理论可以应用于阵列测向[12],需要对阵列测向模型进行改写。将待测空域网格化,划分成一系列离散的角度,如空域的方位角划分成Ns1个网格,空域的俯仰角划分成Ns2个网格。当这些网格点足够密集时,能包含大量来波信号,而真实的来波信号只会出现在极少数的网格点上,因此在空域中信号本身就具备稀疏性。若将方位角和俯仰角联合网格化进行二维测向,无论采用贪婪算法还是凸优化算法重构,计算量正比于总网格数甚至是总网格数的三次方[16],运算量大,难以实时处理。为解决问题,可以不直接划分空域的方位角、俯仰角,而将式(4)中的cosθjcosφj和sinθjcosφj转化成空间角βj和γj,有 (8) (9) 于是X轴阵列测向模型的稀疏表示为 rX(t)=[X-M2(t),…,X0(t),…,XM1(t)]T= (10) 借鉴子空间算法中矩阵重构类方法,提取多快拍数据协方差矩阵最大特征值对应的特征向量作为待重构信号。在式(10)的基础上,先不进行稀疏表示,则X轴阵元接收信号的协方差矩阵RX为 (11) 式中:AX=[α(β1),α(β2),…,α(βp)]为非稀疏表示时X轴阵列导向矢量;RS=E[S(t)SH(t)]为信号协方差矩阵;Rn为噪声协方差矩阵。对RX进行特征分解,可得 (12) 式中:λi、ei为信号子空间特征值和特征向量;λj、ej为噪声子空间特征值和特征向量。当噪声协方差矩阵为理想白噪声时,有[18] (13) 式中:K为信号协方差的秩;bn为en的线性组合因子。K的确定需要知道信源个数p以及信源之间的相关性,但两者均未知,所以K无法确定。考虑最极端的情况,当各信源完全相关,即K=1时,en只能取e1,则有 (14) (15) 式中:V(t)为将e1进行稀疏表示后的系统误差。至此,将e1作为处理对象,既能实现降阶又能解相干。 图2 OMP算法基本流程图Fig.2 Basic flowchart of OMP algorithm 其基本思想是每一次迭代,从过完备字典中选出一个与原始信号最匹配的原子形成支撑集F,通过该支撑集重构信号并计算出与原始信号的残差r,通过该残差选择更匹配的原子并更新支撑集,经过反复迭代重构出原始信号。这种每次只选出一个原子的做法在被动雷达导引头测向场景中是可行的,因为先要对接收信号进行雷达库比对,匹配成功后才开始测向,所以符合要求的信源数不会太多。若每次迭代选择多个原子,则最终累加后很可能超过信源数导致重构失败。但另一方面,迭代的次数直接和信源个数相关,当信源数未知时,需要设计合适的迭代终止条件。可采用稀疏度自适应匹配追踪(SAMP)算法[20],将残差能量减小到一个阈值设置为迭代终止条件,重构信号的同时估计出信源数。SAMP算法与本节算法及其他算法的性能将在第3节对比分析。 本节提出的算法在OMP基础上改进,记为OMP-Number,研究残差能量的变化规律,为信源数估计提供依据。根据图2迭代算法,可得第k次迭代残差rk和第k+1次迭代残差rk+1的关系为 (16) (17) (18) 式中:sup表示上确界。由式(17),可将式(16)改写为 (19) (20) 令Γ(η)=infη(rk)>0,inf表示下确界,代入式(19),可得 (21) (22) 本方法的迭代次数是能估计的最大信源数,为X轴阵元数减1,即M1+M2,这对于导引头小型天线阵而言是可行的,不会增加过多运算负担。另一方面,在噪声的影响下,若迭代次数过多,残差的能量可能不降反增,这时由式(22)估计出的信源数会明显偏大,为预防这一问题,提高算法稳健性,一经发现残差能量变大,应立即退出迭代。 综上所述,本文提出的OMP-Number方法流程如图3所示。 图3 OMP-Number方法流程图Fig.3 Flowchart of OMP-number algorithm OMP算法需要信源数已知作为前提条件,本方法在OMP算法的基础上,做出了三点改进,以实现信源数估计。一是以接收数据协方差矩阵的最大特征值对应的特征向量为处理对象,实现降阶和解相干。二是推导出式(22)作为目标函数估计信源数。三是将子空间算法和压缩感知算法相结合,可实现少快拍甚至单快拍下的信源数估计。 将本文改进的算法OMP-Number与已有算法:稀疏度自适应匹配追踪(SAMP)、最小描述长度(MDL)、盖氏圆(GDE)进行信源数估计性能比较。SAMP基于压缩感知,对相干信号不敏感。MDL和GDE基于子空间,需要专门的解相干处理,故在估计信源数之前进行前后向空间平滑(FBSS)处理,综合后分别为MDL-FBSS和GDE-FBSS算法。 仿真条件:p=2个远场窄带相干信号入射,载频均为3 GHz,分别为雷达信源和诱饵信源;两个信源的方位角、俯仰角分别为θ1=31°,φ1=61°和θ1=41°,φ1=71°;导引头天线阵轴相邻阵元间距为信号波长的一半。若非专门说明,采样均为单快拍,信源功率相同,噪声为高斯白噪声,信号与噪声独立。信源数估计成功率定义为μ=m/N×100%,其中,N为蒙特卡洛实验次数,设为500次,m为信源数估计成功次数。即相同条件下的信源数估计实验重复500次,统计估计成功次数。 SAMP算法,由于本场景为被动雷达导引头测向,能同时匹配雷达库的信源数不会太多,可将迭代步长设为1。但迭代终止时残差能量的阈值设定取决于噪声,在理想无噪情况下一般设为10-6,有噪情况下需测试设定。基于上述仿真条件,测试可得残差能量阈值、估计成功率、信噪比(SNR)三者的数值关系如表1所示。 表1 SAMP算法残差能量阈值设定在不同信噪比下的估计成功率Tab.1 The estimation sucess rate of SAMP algorithm in residual energy threshold setting under different SNR % 因此,将SAMP算法残差能量阈值设定为10-1。 设置信噪比均为SNR=20 dB,单快拍下各算法的信源数估计成功率随阵元数的变化如图4所示。 图4 不同阵元数下各算法性能对比Fig.4 Performance of various algorithm under different number of array elements 现象:除MDL-FBSS外,各算法的估计成功率均随阵元数的增多而升高。OMP-Number在阵元数为6时就能接近100%地估计准确,SAMP和GDE-FBSS需要大量的阵元数才能估计准确,MDL-FBSS则不能适应单快拍条件。因此,采用OMP-Number算法估计信源数更能满足被动雷达导引头空间尺寸受限的应用场景。 原因分析:对于单快拍采样,样本就是各阵元接收信号的单次采样。阵元数越多,样本数就越多,参数估计就会更准确。因此各算法的估计成功率均随阵元数的增多而升高。OMP-Number和SAMP同属压缩感知稀疏重构类算法,要实现信号的精确重构,有最小采样数要求。但本文算法的目标不在于精确重构原始信号(精确重构也没必要采用贪婪算法,可采用凸优化等算法),而是通过处理少量的压缩采样数据实现信源数的准确估计,所以阵元数可突破最小采样数的限制。但SAMP仍需大量阵元数是因为其迭代终止条件对噪声很敏感,本次实验是在SNR=20 dB条件下,对于SAMP而言还是偏低了,接下来会有成功率随信噪比变化的实验。而基于子空间的MDL-FBSS和GDE-FBSS需要子空间分解后进行数理统计,单快拍下难以保证数据量的有效积累,所以性能较差。 设置阵元数为6,单快拍下各算法的信源数估计成功率随信噪比的变化如图5所示。 图5 不同信噪比下各算法性能对比Fig.5 Performance of various algorithms under different SNR 现象:OMP-Number和SAMP的估计成功率均随信噪比的提升而升高。OMP-Number在SNR=10 dB时,成功率超过90%;SAMP在SNR=50 dB时,成功率仍未达到80%。GDE-FBSS在低信噪比时估计成功率高于高信噪比,出现反常。 原因分析:当信源数较少时,GDE-FBSS有可能误估计成功,但其在低信噪比时成功率不足70%、高信噪比时成功率为0,说明该算法并不可靠,在本文研究的场景(少量阵元、单快拍)下失效。OMP-Number和SAMP有效,但需要较高的信噪比。SAMP明显对噪声更敏感,其在噪声环境下无法收敛,从而引入错误的原子导致算法失效。OMP-Number所需信噪比远小于SAMP,且无需人为设定残差能量的阈值,但在SNR=0 dB甚至更低时性能不佳,这是少阵元和单快拍的极端条件所致。 阵元数为6,信噪比SNR=10 dB时,各算法的信源数估计成功率随快拍数的变化如图6所示。 图6 不同快拍数下各算法性能对比Fig.6 Performance of various algorithms under different number of snapshots 现象:随着快拍数的增加,各算法的估计成功率均有提高。特别是GDE-FBSS和MDL-FBSS,成功率随快拍数增多而大幅提升。OMP-Number在单快拍时成功率已较高,多快拍时性能更佳。SAMP成功率也能随快拍数增多而提高,但到60%出现瓶颈。 原因分析:GDE-FBSS和MDL-FBSS基于子空间,需要多快拍保证数据有足够的积累才能获得较好估计性能。SAMP还是对噪声太敏感,在阵元数一定的情况下,需要较高的信噪比甚至无噪环境才能估计准确,若信噪比达不到要求,只提高快拍数,则无法突破估计成功率瓶颈。 阵元数为6,信噪比SNR=20 dB,单快拍,设置雷达的方位角、俯仰角分别为θ1=31°,φ1=61°,诱饵的方位角、俯仰角为θ2=31°+δ,φ2=61°+δ,δ为两信源角度间隔。各算法的信源数估计成功率随信源角度间隔的变化如图7所示。 图7 信源不同角度间隔下各算法性能对比Fig.7 Performance of various algorithms under different angle interval 现象:在本次实验条件下,GDE-FBSS和MDL-FBSS已完全失效。OMP0Number和SAMP的估计成功率随信源角度间隔增大而提高,且OMP-Number估计成功率明显高于SAMP。OMP-Number在信源间隔2°时估计成功率超过90%,在信源间隔7°时估计成功率接近100%。 原因分析:理论上阵元个数越多,测向分辨率越高。但本文提出的算法是基于压缩感知理论估计信源数,所需采样数相对较少,因此能在较少阵元数、单快拍、较小角度间隔时具备较高的分辨率。 在实验二的基础上,将各信源的功率设为随机,得到信源数估计成功率随信源功率的变化如图8所示。 图8 信源不同功率下各算法性能对比Fig.8 Performance of various algorithms under different source power 现象:相比实验二,OMP-Number和SAMP的性能均有下降,均需要更高的信噪比才能保证估计成功率。 原因分析:信源功率相同时,在一定信噪比下,各信号功率和噪声功率有确定的关系。而当各信源功率随机时,虽然各自信噪比确定,但某信源功率可能与另外信源的噪声接近甚至更小,导致难以检出。另外,GDE-FBSS的反常现象已在实验二中分析。 本文提出了一种基于压缩感知的被动雷达导引头估计信源数方法,并通过仿真实验得到验证。该方法的特点和优势在于以下四点: (1)基于压缩感知稀疏重构理论,破解传统子空间类算法在单快拍下信源数估计性能不佳的难题。 (2)改进正交匹配追踪算法,研究残差的变化规律,并构造目标函数估计信源数,能适应单快拍、少阵元、相干信号的场景。 (3)通过数据协方差矩阵最大特征值对应的特征向量实现降阶和解相干处理,子空间算法和压缩感知算法相结合,可灵活设置单快拍或多快拍采样,兼容性较好。 (4)该方法虽然在单快拍、阵元数少、信号相干的极端情况时估计成功率较高,但需要较高的信噪比,待后续研究进一步优化。2.2 阵列测向模型的稀疏表示

2.3 降阶及解相干处理

2.4 改进的正交匹配追踪算法估计信源数

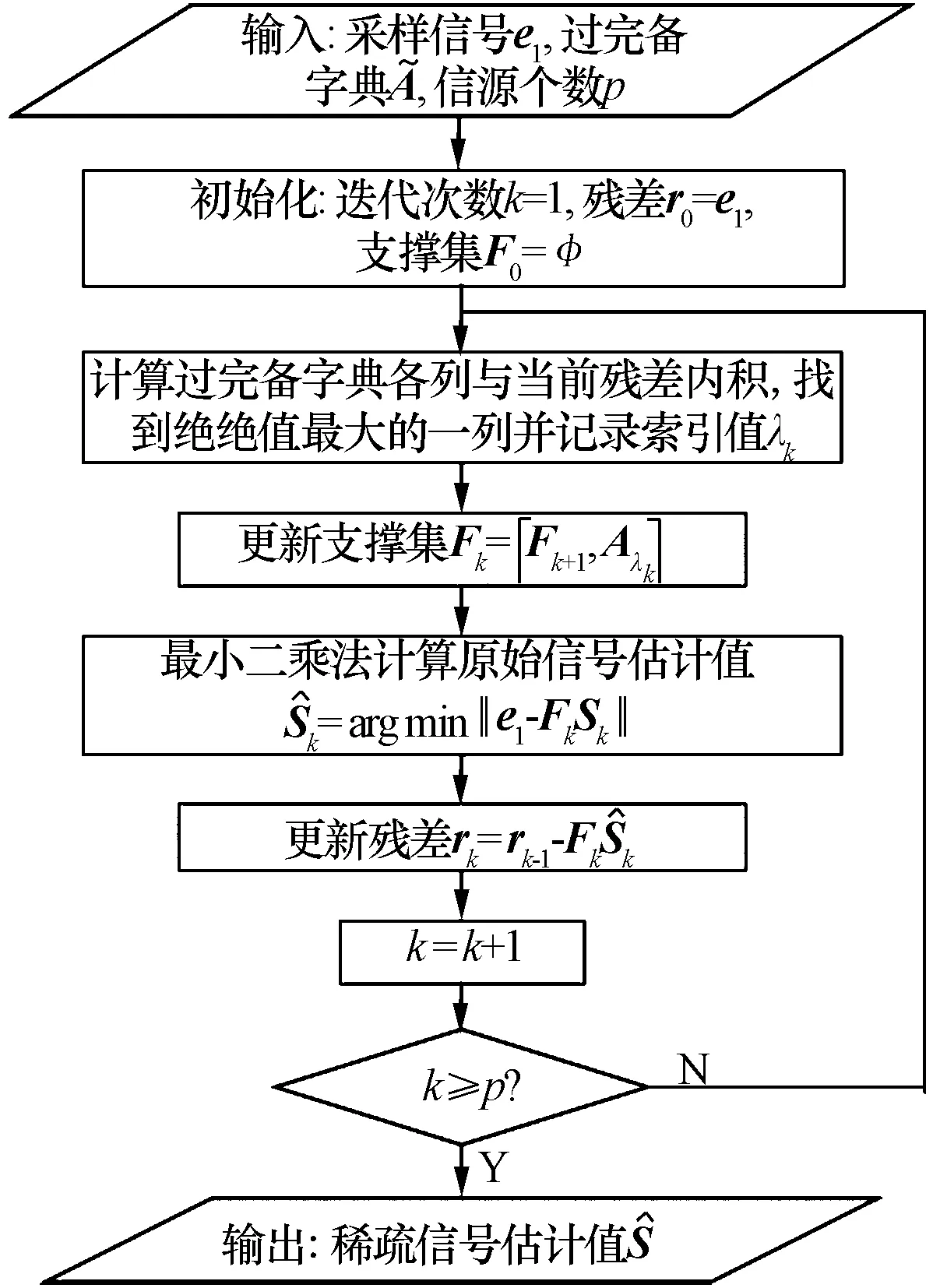

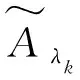

2.5 方法步骤

3 仿真结果分析


3.1 实验一:不同阵元数下,各算法性能对比

3.2 实验二:不同信噪比下,各算法性能对比

3.3 实验三:不同快拍数下,各算法性能对比

3.4 实验四:信源不同角度间隔下,各算法性能对比
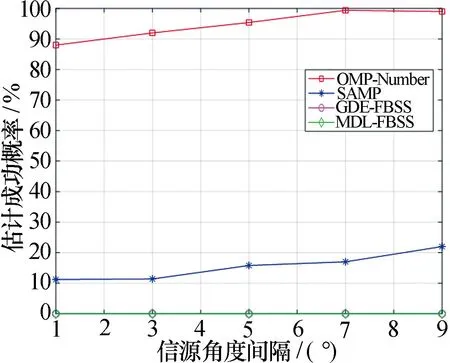
3.5 实验五:信源功率不同下,各算法性能对比
4 结束语
