基于实测数据立式热水储能罐罐壁力学特性分析*

2024-04-01李雄彦魏金刚薛素铎

建筑结构 2024年5期

李雄彦, 魏金刚, 薛素铎

(北京工业大学城市建设学部，北京 100124)

0 概述

热水储能是在用热低谷期,把暂时不需要的热量、来自于机组或可再生能源产生的多余电能转化成的热量,以水为蓄热载体储存在储能罐中。在用热高峰期将热量释放出来再利用,热水储能罐(简称储罐)具体工作流程如图1所示。蓄热储能技术[1-2]能有效解决能量在时间和空间上供需不匹配问题,区域供热[3]电厂设置热水储能罐可减少调峰锅炉的启用,充分利用热电联产技术[4]的优势,提升经济效益。

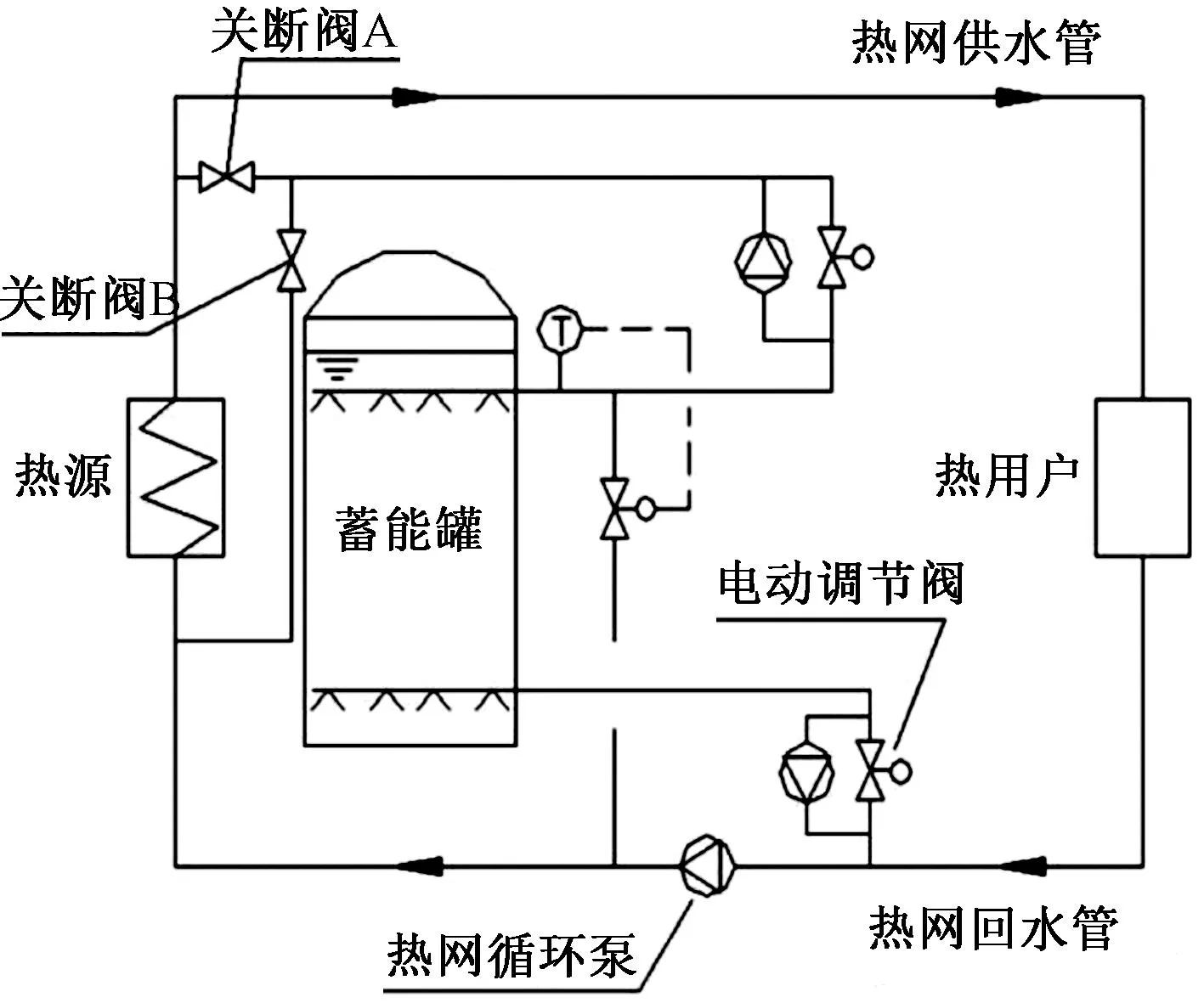
图1 热水储能罐工作流程图

图2为本文所研究的立式储罐的构造示意图,其受力复杂,储液高度直接影响储罐的力学特点,随着储液高度的增加,底部应力也逐渐增大,最大应力一般出现在在底部第一圈或者第二圈罐壁上[5]。储罐在我国的应用尚处于起步阶段,目前缺乏此类罐体的设计与施工标准[6]。

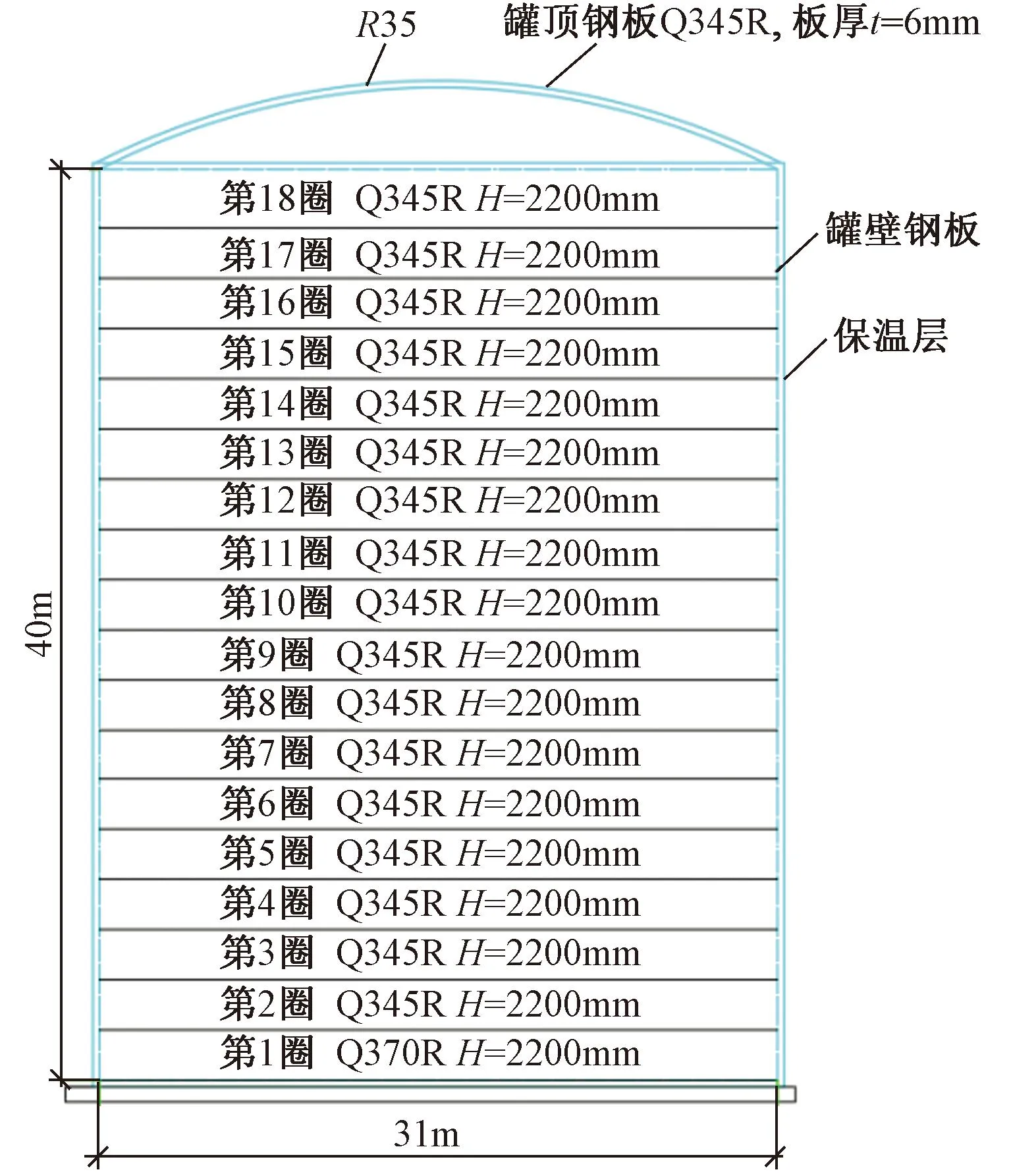
图2 立式储罐构造示意图

随着社会需求的增长,储罐体积不断趋于大型化,为了降低成本,在设计上壁厚与内径的比值也越来越小,使得结构的应力比不断增加,掌握储罐运行过程中的力学性能,是确保其安全性的关键。对储罐的结构进行健康监测是考察其受力和安全状态最直接的方法,但由于实际监测所需时间和成本较高,有限元模拟方法被广泛应用于从此。但是有限元分析结果是否准确又有待考证,合理的有限元分析是立式储罐力学性能研究的关键[7]。对此,不少学者对储罐有限元分析方法开展了相关研究。王莉莉、付世博等[8]对某大型原油储能罐的模型进行了简化研究,但没有考虑风荷载、不均匀沉降、地震作用等影响因素;顾思阳、柴庆友等[9]通过研究立式原油储能罐罐壁应力变化,得出罐壁主要受环向应力影响,中上部罐壁变形较大。卞学吉、王茂延等[10]研究立式储能罐罐壁的应力和位移变化,得到壁板下部以轴向弯曲应力为主,在高度3m以上部分以环向弯曲应力为主,罐壁最大变形位置出现在中上部和上沿处。计静、宋华宇[11]等研究立式储罐罐壁沿高度环向应力分布规律,得到其受力最大部位在罐壁的下部,并给出了设计建议。陈松、王旭[12]通过研究大型油气罐的健康监测系统,给出了监测系统的组成以及传感器的优化布置。袁朝庆等[13]建立一套应用光纤传感技术的大型储罐监测系统,并对测点进行了优化设计。周云双[14]研究开发储罐健康监测系统,对关键部位的应变温度进行实时监测,通过实时反馈信息确保储罐安全运行,为立式储罐健康监测提供了重要参考价值。

虽然目前国内外学者对储罐有限元分析方法开展了相关研究,但是基于工程实践的实测数据进行验证的较少。因此,本文基于某30000m3储罐项目,对罐体进行温度和应力长期实时监测,依托远程监测技术采集运行状态下罐壁应力和温度数据,基于应力监测结果,验证考虑罐底摩擦接触约束有限元分析方法合理性;依托温度监测数据对立式储罐热力耦合作用下罐壁位移以及应力分布规律进行分析研究。

1 立式储罐有限元模型

1.1 工程概况

以某30000m3的立式圆柱形钢制焊接非锚固储罐为研究对象,构造如图2所示,外立面如图3所示。该储罐主要由罐顶、罐底、罐壁三部分组成,整体罐高43.62m,罐壁内径为31m,罐底中幅板厚度为10mm,边缘板厚度为20mm;中幅板直径为26.9m,边缘板内直径为26.9m,外直径为31.18m;罐壁最底端厚度为36mm,从罐壁最底端开始每往上增加2.2m,厚度就会减小2.0mm,到罐壁最顶端厚度为8mm;罐顶内径为31m,矢高为3.5 m,厚度为6mm。

图3 某30 000m3立式热水储能罐

1.2 材料参数与荷载

由于储罐为非锚固,罐壁的位置落在刚度相对大的钢筋混凝土环梁上,环梁中间是砂石垫层,垫层、环梁、罐体材料不同,建模时设置与实际相对应的弹性模量和泊松比,材料参数如表1所示。

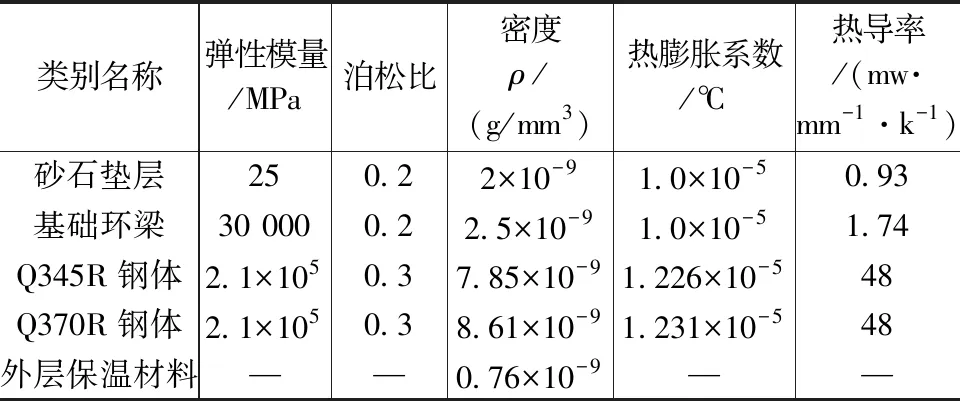
表1 立式储罐材料基本参数

1.3 有限元模型建立

立式储罐有限元分析的难点在于地基情况的模拟,2006年,陈志平等[15-16]在对原油储罐的有限元分析中就提出用地基沉降量的方法来代替之前的弹性杆单元法建模,验证了在沉降量法基本模型的简化下计算得到罐底的径向应力与实测值最接近;并参考油罐地基的建模方法,得到在静水压力和罐体自重的影响下,放置在混凝土环梁基础环梁上的罐底部分基本不发生沉降,但是放置在环梁内部铺设砂子垫层的部分会发生沉降。

对地基的简化假设也有很多种,假设不同罐体的变形情况也不一样,对罐底板和罐壁都有一定的影响,以往的模型大都忽略了基础的不均匀沉降导致的底板翘曲[17],计算应力与实际不符,对上部结构的影响也未做出合理的判断;罐壁与罐底连接处应力分布较复杂[18]。为了较为精细化地分析罐壁内力,计算模型考虑基础的影响。建立基础模型并赋予砂石垫层、环梁相应的弹性模量和材料属性,在垫层、环梁和罐底的接触面建立相互作用,并设置接触,摩擦系数为0.2,基础采用实体单元,储罐采用壳单元,有限元模型如图4所示。

图4 划分网格后的储罐各部位有限元模型

2 立式储罐数据实测

2.1 实测数据采集方案

结合项目背景,对储罐进行监测方案设计,主要是传感器优化布置,坚持基本原则的同时参照其受力特性并结合逐步累积法[19]确定传感器数量。为获取立式储罐的罐壁应力与温度分布情况,测点分为水平测点和竖向测点,水平测点主要监测环向的应变与温度,竖向测点主要监测竖向应变。在布置中,同时考虑安装的可操作性,沿着爬梯附近布置温度测点,由于储罐下部承受的水压力大于上部,所以总体上,下部的传感器布置密集,上部稀疏,逐级递减,测点布置如图5所示。

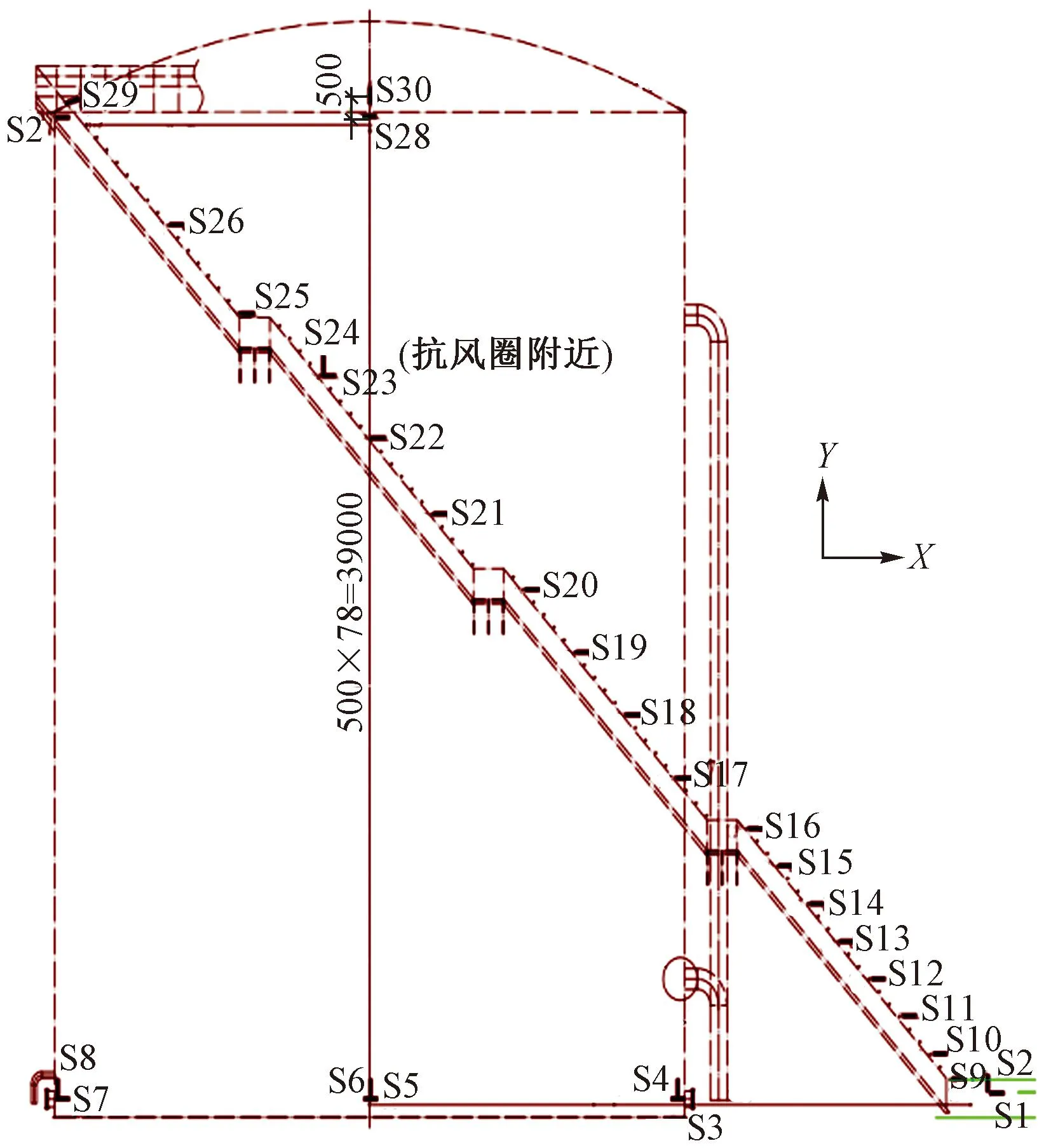
图5 测点布置详图

2.2 数据传输与采集

数据采集选择BGK-Micro 40自动化数据采集仪,设置采集频率为每小时2次,如图6所示,传感器与数据采集仪之间采用有线传输,数据采集仪与监控中心采用无线数据传输方式,增加无线通讯模块,将数据传输到服务器。

图6 数据采集过程图

3 有限元分析与验证

在ABAQUS有限元模拟中,压应力为负、拉应力为正。罐壁是对称的,沿任意高度方向提取应力数据均能反映出其变化规律,本文取0° (X轴)位置沿高度方向选择路径path-1提取模拟数据用于与实测数据结果的对比。

如图7(a)所示,通过有限元模拟(底部采用摩擦接触约束)得到的罐壁底部环向应力为89MPa,环向应力最大值为170MPa,出现在高度2.2m处,向上波动变化呈减小趋势,从30m高度以上后急剧减小。如图7(b)所示,在罐壁底部较近处竖向拉应力为23MPa,1.5m高度处竖向压应力最大值达到63MPa,沿高度向上罐壁竖向应力在0MPa附近徘徊。

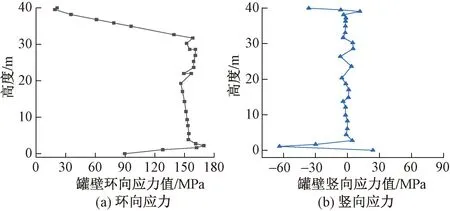
图7 罐壁应力有限元模拟应力分析结果

将实测数据进行分析处理,得到不同时间段罐壁应力实测平均值沿高度的变化曲线如图8 (a)所示。满罐运行状态时主要集中在170～190MPa左右,位置出现在距离罐底上表面2.2 m高度左右;有限元分析与实测数据分析结果显示一致,最大值位置相同,应力值吻合较好,且曲线变化规律一致。

图8 满罐下实测数据分析结果

罐壁底部的环向应力如图8(b)所示,罐壁底部实测环向压应力平均值约为85MPa,此处有限元分析环向压应力为89MPa,两者相差仅5%。通过罐壁底部竖向测点的应力曲线图8 (c)可以看出,底部竖向测点最大竖向压应力约为30MPa,此处有限元分析结果23MPa,两者也较为接近。

ABAQUS有限元模型的罐底变形如图9(a)所示,由图9可以明显看出,罐底的变形与沉降量法[16]下的翘曲情况一致,此建模分析方法正确可行。

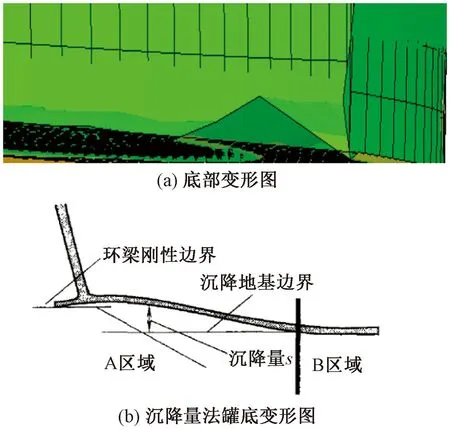
图9 模拟底部变形与沉降量法罐底变形对比

综上所述,通过有限元结果与实测结果的对比分析,验证了有限元建模分析的正确性。同时可以得知立式储罐罐壁最大环向应力出现位置距离罐底2.2m左右处,此位置最薄弱,2.2m以上以受环向应力为主;最大竖向应力出现在距离底部1.5m左右处,为了安全性在设计时应该充分考虑罐壁底部,采取一定的加厚措施。

4 热力耦合下立式储罐力学特性分析

储罐在温度变化下会产生膨胀或者收缩,如罐体受约束影响变形不协调,则会产生温度应力。在实际问题中,热量传递往往是以热传导、热辐射和热对流三种方式组合或顺序出现,由于本文研究的情况是储罐在空气中,由于空气没有辐射吸收能力,所以热传递的方式主要考虑以热传导和热对流的方式发生[20]。而且本模型中的热应力属于与膨胀系数有关的热应力,随着时间的改变,温度的变化始终在-20～98℃之间,对钢材的刚度和柔度没有显著的改变。将采用完全热力耦合法对立式储罐进行有限元模拟分析。

4.1 立式储罐温度分布与简化

立式储罐在空罐情况下温度变化主要受到环境温度的影响,考虑到当地气温情况,取夏季最高气温40℃进行模拟。冬季供暖季正常运行状态时储罐内温度场分布变化很快,且由于布水器的控制,罐内水的温度会出现斜温层[21],但若对每一种变化情况都进行模拟,工作量巨大且较繁琐,固对实测数据进一步处理,取运行阶段各个测点的温度平均值,利用MATLAB软件拟合,得到温度随高度变化如图10所示,并进一步得到立式储罐最常在状态温度随高度变化的经验公式见式(1)。

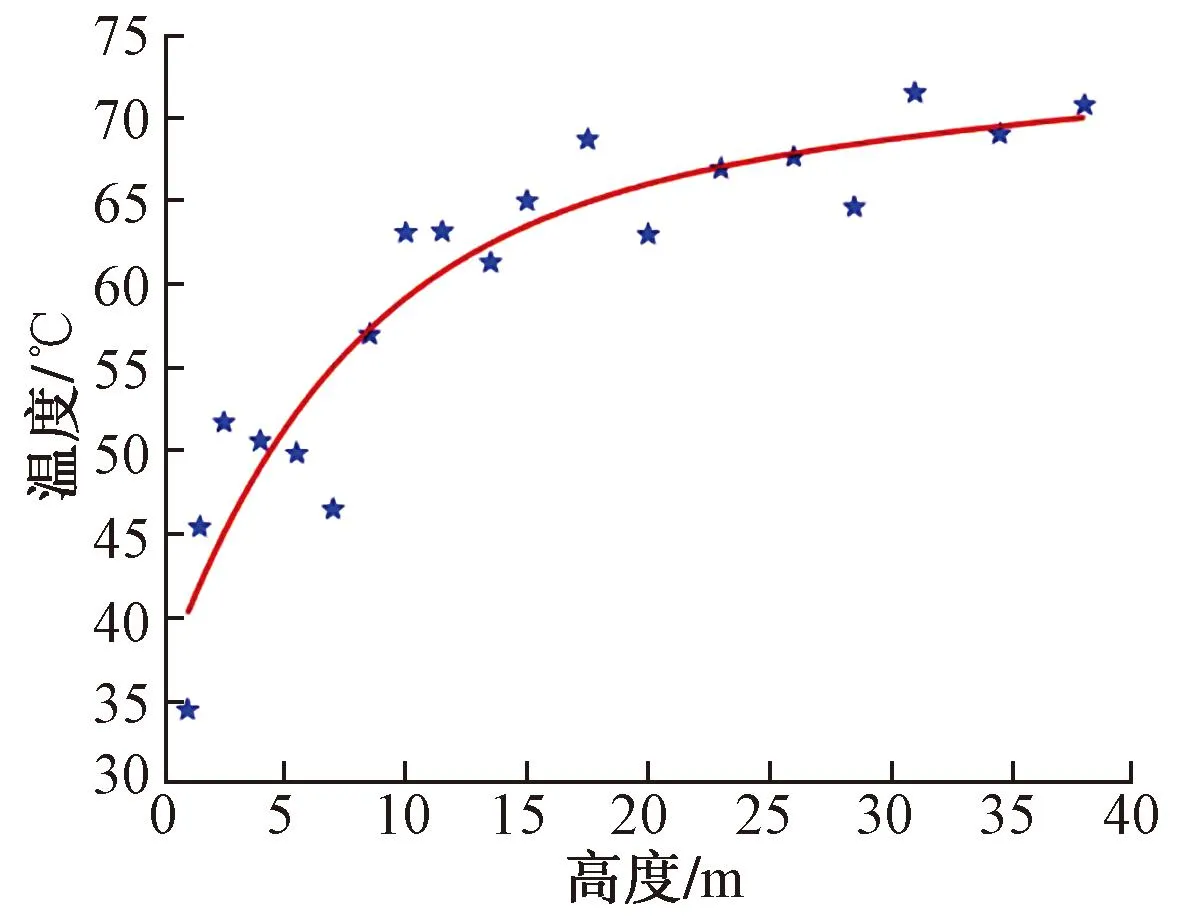
图10 储罐温度随高度变化拟合曲线

f(Z)=a×exp(b×Z)+c×exp(d×Z)

(1)

式中:Z为高度;a～d均为参数,在本监测温度数据中,取a=65.79,b=0.001712,c=-29.13,d=-0.1331。

以式(1)来定义沿高度方向的温度分布,对储罐进行力学特性分析,得出运行状态时温度对力学性能的影响。设置以下工况:1)工况1为重力+气压组合作用;工况2为重力+静水压力+气压组合作用;工况3为重力+气压+温度组合作用;工况4为重力+静水压力+气压+温度组合作用。

工况1、3属于空罐状态,无温度作用时,默认为0℃,有温度作用时温度取夏季最高温度40℃;工况2、4属于满罐状态,无温度作用时默认为0℃,有温度作用时温度取拟合曲线温度值。通过对比分析以上工况,研究温度对罐壁的力学特性影响。

4.2 热力耦合作用下罐壁变形位移

工况1、3下罐壁位移变化如图11(a)所示,由图11(a)可以看出,工况3下,随着温度的升高,罐壁发生膨胀,大大提高了罐壁的变形量,沿高度方向,罐壁位移从8 mm逐渐增加到23 mm,在罐壁顶部位移最大,即温度作用对罐壁上部影响最大,原因是上部壁厚小,更易变形。

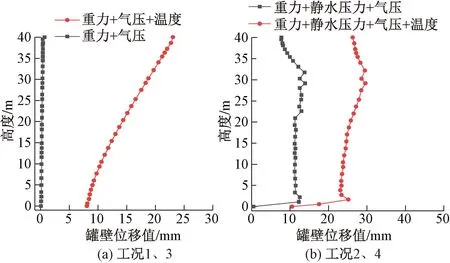
图11 罐壁位移随高度的变化曲线

工况2、4下罐壁位移变化如图11(b)所示,由图11(b)可以看出:罐壁底部在工况4下的位移为11.0 mm,且向上逐渐增大;工况4下罐壁最大位移为29.49 mm,出现在高度30 m处。静水压力对罐壁变形影响较大,罐壁温度升高使得罐壁发生膨胀变形与静水压力产生的变形叠加,且温度作用引起的罐壁位移大于静水压力引起的罐壁位移。

4.3 热力耦合作用下罐壁环向应力分析

图12(a)为工况1、3作用下罐壁环向应力随高度变化曲线。从图12(a)可以看出,没有静水压力作用时,温度作用对罐壁的环向应力的影响体现在罐壁两端,对比工况1和工况3,温度为0℃时,罐壁底部环向应力值为11.79MPa,温度升到40℃时,对应位置环向应力为-0.31MPa,温度由0℃上升到40℃时罐壁顶部环向应力值由-2.45MPa变为-9.45MPa,可以明显发现,当温度升高时,产生环向压应力,因为温度应力是被动应力,在罐壁受到温度荷载的作用时,罐壁会发生膨胀变形,由于受到罐底和罐顶的约束,不能自由变形,产生环向压应力。

图12 罐壁环向应力随高度变化曲线

从环向应力变化曲线图12(b)可以看出,温度作用对罐壁的环向应力的影响仍然主要是罐壁两端,对比工况2和工况4,工况2下,罐壁底部环向应力值为110.27MPa,罐壁底处温度为40℃时,对应位置环向应力为75.63MPa,减小31.4%。温度由0℃上升到75℃时罐壁顶部由环向应力值由7.28MPa减小到2.04MPa,减小71.9%,说明罐壁两端环向应力受温度荷载影响显著,温度越高,影响越大。在静水压力作用下,罐壁产生环向拉应力,温度升高,使其产生环向压应力,两者会部分抵消,但是与工况1、3相比,情况不同的是静水压力使得罐壁产生的环向拉应力占主导作用,温度升高到一定范围内,反而可以减小罐壁两端环向拉应力,但若温度低于0℃时,会产生环向拉应力与静水压力产生的环向拉应力叠加,使得罐壁两端环向拉应力增加。

4.4 热力耦合作用下罐壁竖向应力分析

从图13(a)可以看出,温度仅对罐壁底部(1.5m高度范围内)竖向应力的影响较大,同样是温度升高,使得罐壁竖向也发生热变形,由于受到罐底的约束,不能自由变形,产生竖向压应力;罐壁底部在0℃时受到竖向拉应力为4.87MPa,温度升到40℃时竖向拉应力变为1.59MPa,减小67.4%,原因是温度升高产生的竖向压应力抵消,罐壁中部应力随高度变化曲线几乎重合,说明罐壁中部受温度的影响不大,罐壁竖向上部不受约束,故产生的温度应力较小。

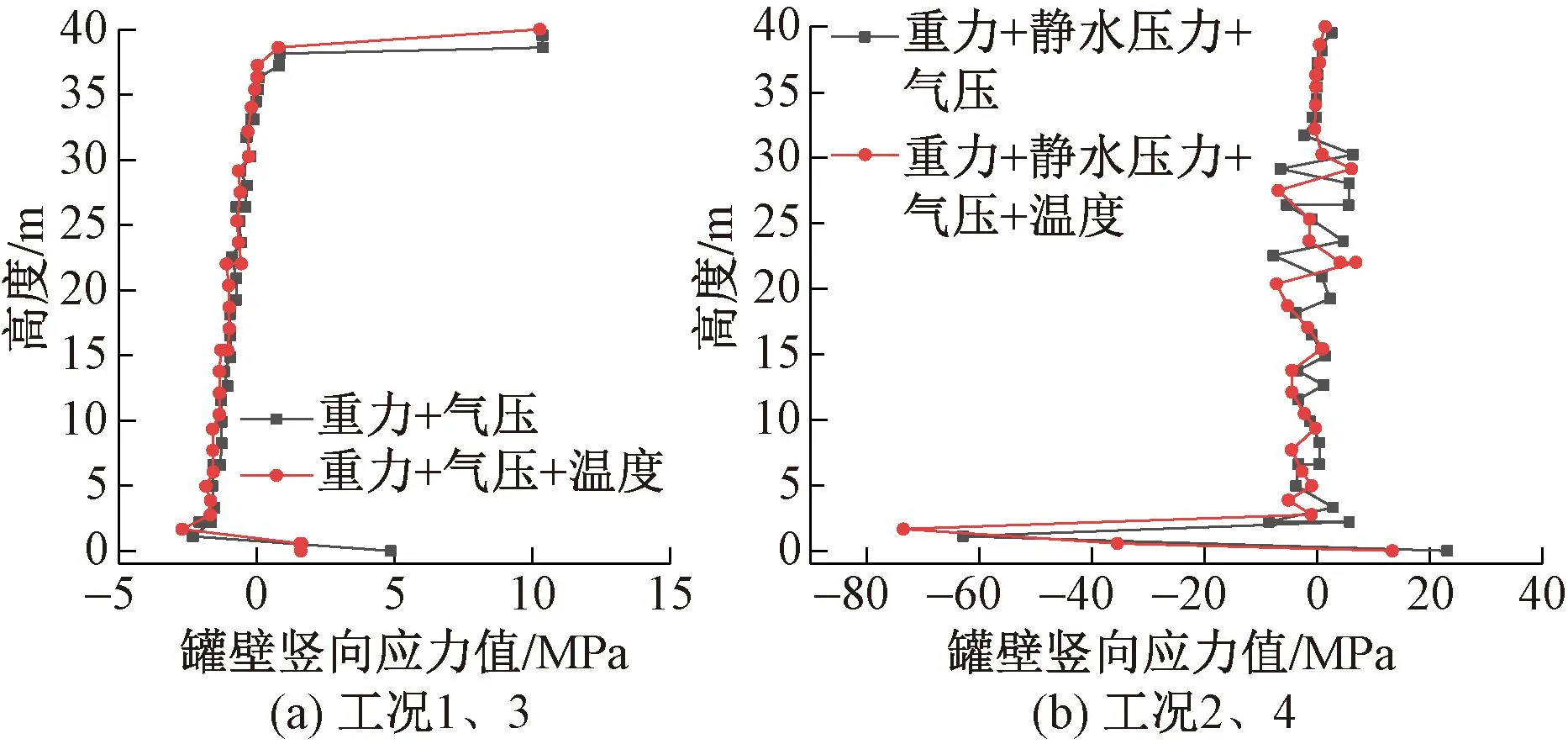
图13 罐壁竖向应力随高度变化曲线

从图中13(b)得知,温度对罐壁竖向应力的影响依然体现在罐壁底部,温度升高产生竖向压应力,最大竖向压应力在1.5 m高度处,工况2最大竖向压力62.91MPa,工况4最大竖向压应力73.55MPa,此处温度50℃左右,增大14.5%;罐壁0m高度处在0℃时受到竖向拉应力为22.13MPa,温度升到40℃时竖向拉应力变为13.26MPa,减小40.1%,在1.5 m高度以上部位,温度虽然一直在上升,但竖向应力没有受到温度的影响。