基于改进GM(1,1)模型的生活用水量预测

2024-03-31高华昆陶月赞

合肥工业大学学报（自然科学版） 2024年3期

高华昆, 陶月赞, 杨杰

(合肥工业大学土木与水利工程学院,安徽合肥 230009)

随着城市化的发展和居民生活水平的提高,生活用水量持续增加,生活用水供需矛盾日益突出[1]。因此精准合理地预测生活用水量,有助于缓解用水供需矛盾,也是水资源保护、管理的研究热点。生活用水量从较长时间看,具有逐年增长的趋势,为其预测奠定了基础。常用的用水量预测方法有城市综合指标法、系统动力学法、灰色预测模型法等[2-4]。

灰色系统理论认为任何随机过程都可以看成一定时空区域内变化的灰色过程,灰色系统即部分信息已知、部分信息未知的系统,该理论是文献[5]提出的,灰色预测模型是灰色系统理论的一部分。对于生活用水量的预测,已知信息为用水量,但是影响用水量的其他因素难以明确得知,即为未知信息,如气候、行政管理措施、人口规模等,因此可将其视为灰色系统,灰色预测模型是适用的[6]。该模型广泛应用于人口预测、经济预测、电力预测等[7-9]。自GM(1,1)模型提出至今,国内外学者不断对其进行改进,文献[10]基于新信息优先原理提出非等间距GM(1,1)优化模型,改进后的模型能够充分利用信息,从而提高预测精度;文献[11]利用拉格朗日中值定理将背景值构造为与初始值相关的变量,有效提高模型的预测精度;文献[12]分析非等间距GM(1,1)模型中的背景值,提出用Newton插值和数值积分中的Newton-Cores、Gauss-Legendre公式分别重构模型中的背景值,数据模拟结果充分说明新模型的有效性和优越性;文献[13]通过对非等间距原始序列背景值进行改进,拓宽GM(1,1)模型的适用范围和精准度。

国内外学者大多引入积分差值、向量等方法改进GM(1,1)模型,这些方法虽然取得不错的预测效果,但是较为烦琐,不利于预测结果的计算。通过对GM(1,1)模型的研究,发现灰色预测模型的误差来源主要是初始条件和背景值[14-15]。本文在上述研究的基础上引入幂函数优化背景值、原始序列进而改进GM(1,1)模型,并将其应用于河南省生活用水量预测中,以期能用少量的数据进行中长期用水量预测,为城市供水管理、水资源持续利用提供帮助。

1 GM(1,1)模型的改进

1.1 GM(1,1)模型及其局限分析

经典GM(1,1)模型的构造如下,原始序列x(0)={x(0)(1),x(0)(2),…,x(0)(n)}为非负序列,经累加得到:

x(1)(k)={x(1)(1),x(1)(2),…,x(1)(n)}

(1)

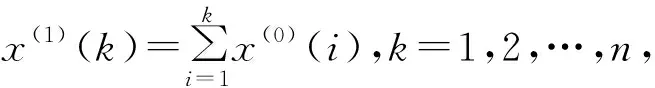
对序列x(1)(k)的紧邻数据求均值,生成z(1)(k)序列,即

z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)

(2)

构造矩阵B与矩阵Y,采用最小二乘法求参数a、b,即

Y=[x0(1)x0(1) …x0(n)]T,

[ab]T=(BTB)-1BTY

(3)

其中:a为发展系数;b为灰色作用量。

GM(1,1)模型的时间响应函数为:

(4)

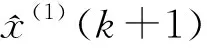
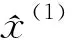
(5)

按照式(1)～(5) 构造的模型即为经典GM(1,1)模型。

通过上述建模分析,可以发现经典GM(1,1)模型存在如下缺点:

1) GM(1,1)模型的拟合和预测精度与a、b值有关,a、b的计算数值依赖于原始序列和背景值,因此式(2)的构造是造成拟合误差的因素之一。

1.2 GM(1,1)改进模型

经典GM(1,1)模型在构造紧邻均值序列z(1)(k)时,所使用的方法为式(2)。此方法使得x(1)(k)中的每个数据均处于同等地位,导致新数据比旧数据没有优势,从而影响预测精度。为了削弱此种影响,使新数据占主导地位,文献[12]运用Newton-Cores、Gauss-Legendre公式进行改进背景值,此方法较为烦琐,不利于计算。本文构造新的序列Z(1)(k),即

(6)

式(6)对原有序列式(2)进行改进,新序列可抽象为幂函数。当N取2时,Z(1)(k)与z(1)(k)两序列相同。

按式(1)、式(6)、式(3)～(5) 顺序重新构造GM(1,1)模型,即优化背景值进而改进GM(1,1)模型,为便于比较,本文将此种构造方法记为模型Ⅱ。

经典GM(1,1)模型在使用过程中需要原始数据离散且非负,通过一次累加生成削弱随机性、有规律的离散序列。为增大此种影响,使原始序列随机性减小、规律性增大,更能适合GM(1,1)模型。文献[16]引入缓冲算子对原始序列进行改进,缓冲算子虽然能有效减小预测产生的误差,但是需要满足不动点公理、信息充分利用公理、解析化和规范化公理方可使用。同时,当原始序列为振荡序列时,预测效果不如单调增长序列或单调衰减序列,而实际工程中很多原始数据是振荡序列。因此本文在前人研究的基础上进行总结,采用新的序列X(0)(k)代替原始序列x(0)(k)进行模型优化改进,新序列也可抽象为幂函数表示,即

(7)

按式(1)、式(7)、式(2)～(5) 顺序重新构造GM(1,1)模型,即优化原始序列进而改进GM(1,1)模型,本文将此种构造方法记为模型Ⅲ。

1.3 模型检验

对灰色预测模型及其相关改进模型的检验方法较多,常用的预测性能检验方法主要有均方误差、均方根误差、标准误差、平均相对误差等[6]。几种检验方法相似,为了运算简便,本文选取平均相对误差法进行预测性能检验。常用的预测精度检验方法主要有残差检验、灰色关联度检验、后验差检验[17]。残差检验仅对残差序列进行检验从而得出模型的预测性能,检验序列较少,因此本文采用灰色关联度检验和后验差检验。

令εi为原始数据与预测数据的残差,即

在锚杆支护应力场试验台上安装1根锚杆，对比分析金属托盘和金属托盘+木垫板2种情况下锚杆预紧力损失、转矩转化、支护预应力场分布。锚杆采用现场采取的长度2 400 mm、直径22 mm的左旋无纵肋螺纹钢锚杆。锚固方式为加长锚固，锚固长度1 200 mm。为了更好地模拟井下实际工作状态，使用井下常用的金属网作为护表构件，安装结果如图3所示。

1) 平均相对误差。平均相对误差检验是对模型预测和仿真性能的检验,可以有效地反映出预测模型的真实值与预测值之间的差异[18],即

(8)

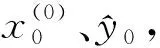
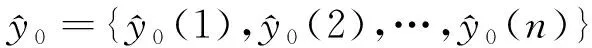
(9)

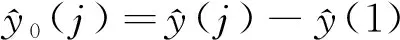
(10)

其中:i=1,2,…,n;j=1,2,…,n。

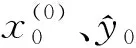
(11)

其中

3) 后验差检验。后验差检验主要由均方差比C、小误差概率P2个检验组成,该方法以残差序列为研究对象,检验残差的概率分布[21]。

(12)

(13)

(14)

(15)

平均相对误差检验是模型预测精度方面的检验方法,绝对关联度检验、后验差检验是模型拟合精度方面的检验。相对误差越小,模型预测精度越高;C越小,模型预测精度越高,表明原始数据很离散,而模型计算值与实际值之间并不太离散;P和C同时进行精度刻画,P越大,精度越高,表示残差与残差平均值之差小于给定值0.674 5S1的点较多[22]。通过检验可将模型划分为4个等级,模型精度等级参数取值见表1所列[23]。

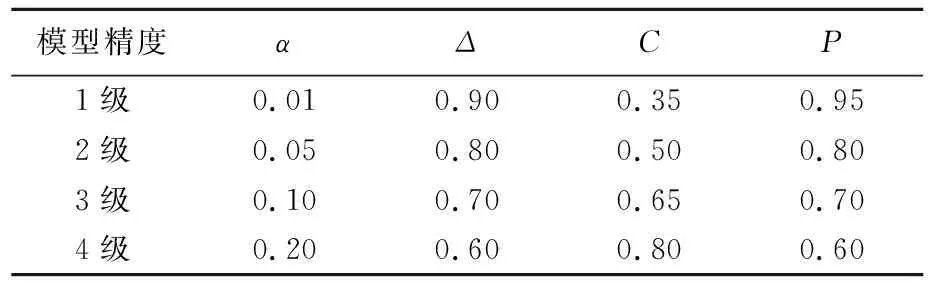
表1 模型精度等级参数取值

2 实例分析

2.1 数据来源

为了便于与其他改进方法进行比较,本文采用文献[24]提供的河南省2012—2018年生活用水量数据及改进模型(记为模型Ⅰ)进行横向对比,结果见表2所列。通过查阅《河南省水资源公报》,利用2019—2020年实际用水量数据作为预测检验。模型Ⅰ与文献[10]所提出的改进模型相似,改进背景值计算方法进而改进GM(1,1)模型。

表2 河南省2012-2018年居民生活用水量单位:108m3

2.2 模型构建

对表2中的数据分别使用经典GM(1,1)模型、模型Ⅰ、模型Ⅱ、模型Ⅲ建模,对生活用水量进行模拟预测。模型Ⅱ、模型Ⅲ构建时,N与M的选择至关重要,经过多次重复试验,N取3、M取2时,效果最好。

经典GM(1,1)模型为:

(16)

模型Ⅰ为:

(17)

模型Ⅱ为:

(18)

模型Ⅲ为:

(19)

通过式 (16)～(19) 求出4种模型的模拟预测值和误差结果,见表3所列。

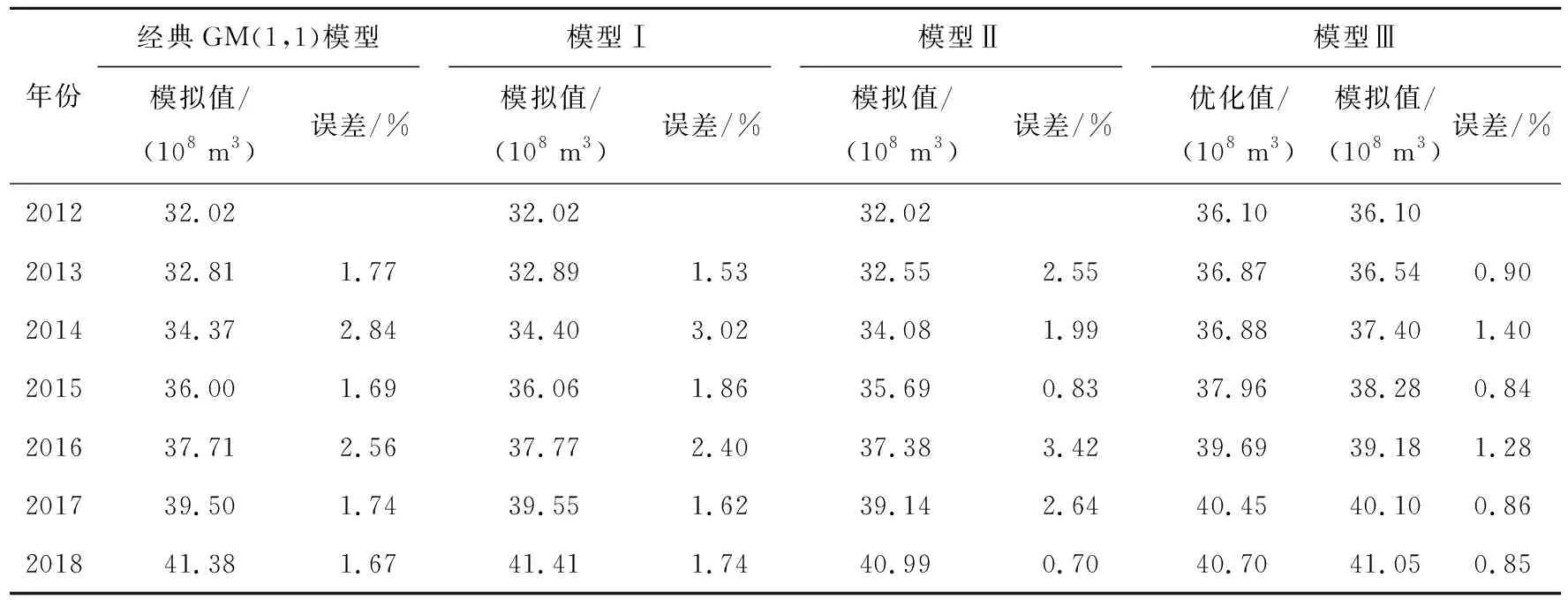
表3 2012-2018年4种模型用水量模拟结果对比

由上述分析及表3可知:模型Ⅰ、模型Ⅱ同为优化背景值进而改进GM(1,1)模型,但模型Ⅰ出现的最大误差年份为2014年,误差为3.02%;模型Ⅱ出现的最大误差年份为2016年,误差为3.42%;GM(1,1)模型的最大误差年份为2014年,误差为2.84%。对比模型Ⅰ、模型Ⅱ发现使用积分的方法改进背景值优于引用幂函数的方法改进背景值,但两者改进后的模型均出现了最大误差大于GM(1,1)模型。模型Ⅲ对比GM(1,1)模型,则最大误差大幅减小。模型Ⅲ出现最大误差的年份也是2014年,但仅为1.40%。

经典GM(1,1)模型、模型Ⅰ、模型Ⅲ产生最大误差的年份为2014年,通过2014年实际用水量以及预测用水量发现4种模型的预测值均大于实际值。此种现象普遍存在于GM(1,1)模型在进行等间距预测时,原始数据变化差异较大,从而造成预测误差变大。模型Ⅲ虽进行了优化原始序列,减少此类误差产生,但无法消除。

2.3 模型检验

采用式(8)～(15)检验4种模型的模拟预测效果,结果见表4所列。

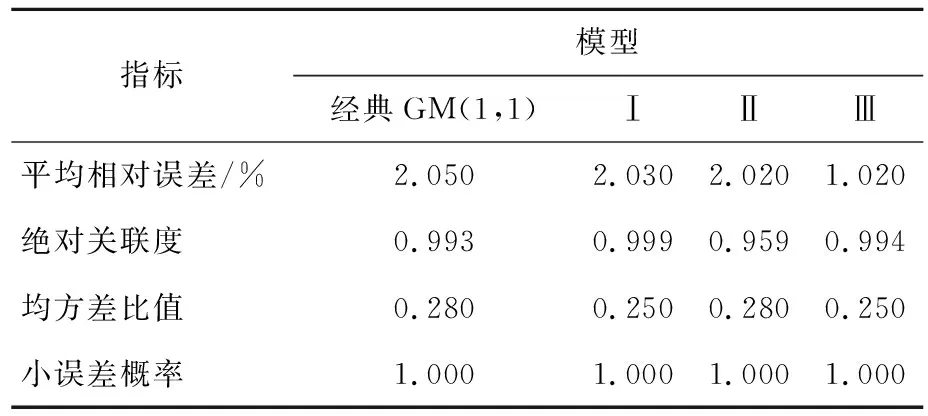
表4 4种模型的精度检验

由表4可知,4种模型在绝对关联度、均方差比值和小误差概率检验相差不大,绝对关联度大于0.900,均方差比值小于0.350,小误差概率大于0.950。在不计入平均相对误差指标分析时,4种模型的精准度为一级精度模型。通过平均相对误差检验可以发现,模型Ⅲ的平均相对误差最小,经典GM(1,1)模型、模型Ⅰ、模型Ⅱ产生的平均相对误差基本相同,约为模型Ⅲ平均相对误差的2倍。

本文所采用的2种改进方法在模型拟合精度方面没有显著提高,但模型Ⅲ在预测精度上有显著提高,模型Ⅱ却无明显变化。这表明模型Ⅲ更具优越性,具有较好的工程应用价值。

2.4 用水量预测

通过上述分析可知模型Ⅲ更具预测的优越性,但上述4种模型在精度等级上都可以进行中长期用水量预测。

为了检验模型Ⅲ是否更适合河南省生活用水量预测,本文根据上述4种模型,通过式(13)～(16)预测2019—2020年用水量,结果见表5所列。

表5 2019—2020年4种模型用水量误差对比

虽然4种模型都适用于河南省生活用水量预测,但由表5可知,模型Ⅲ进行河南省生活用水量预测时效果最好。4种模型的平均相对误差分别为4.76%、4.91%、3.70%、0.63%,模型Ⅲ2019年、2020年的误差分别为0.99%、0.27%,预测精度远超前3种模型,更适合进行河南省生活用水量预测。模型Ⅲ的预测结果较为理想,但在实际问题使用时会受到其他因素的影响,如引江济淮工程、《地下水管理条例》施行等,造成供水水源、水量发生变化。这些变化在一定程度上会影响预测结果的精准度,因此在作出预测前要求用水过程不会发生结构性变化。

综上所述,使用模型Ⅲ进行河南省生活用水量预测,预测出2021—2025年用水量分别为44.02×108、45.05×108、46.11×108、47.20×108、48.31×108m3。