基于融合健康因子和集成极限学习机的锂离子电池SOH在线估计

屈克庆, 董 浩, 毛 玲, 赵晋斌, 杨建林, 李 芬

(1. 上海电力大学 电气工程学院,上海 200090; 2. 国家电投风电产业创新中心,上海 200233)

锂离子电池因高能量密度、低自放电率和循环寿命长的优点,被广泛应用在电动汽车和分布式储能系统等多个领域中.然而,这些优势会随着电池寿命的衰减而降低,电池的过度老化可能导致电池系统故障,甚至引发安全事故[1-3].因此,为了避免事故发生和提高电池系统运行的稳定性,对锂离子电池进行实时的健康状态(State of Health,SOH)监测尤为重要[4].

锂离子电池的老化过程十分复杂,是外部和内部因素相互作用的结果.其外部因素包括环境温度、充放电速率、放电深度等;内部因素可以概括为固体电解质界面的分解、锂离子沉淀和镀层等[5].目前,关于锂离子电池SOH的估计方法主要分为直接测量法、基于模型的方法和基于数据驱动的方法[6].直接测量法通过直接计算电池容量和内阻来反映电池的健康状态,包括库伦计数法、开路电压法和阻抗频谱法等[7-9];其计算复杂度较低,但在线运行时需要额外的硬件支持且抗噪能力较差[10].基于模型的方法通过电化学机理或等效电路模拟电池老化现象.一些递归观测器,如卡尔曼滤波[11]、滑模观测器[12]和粒子滤波器[13]等,被用于从充放电过程获得电流、电压数据来更新模型的内阻和容量参数,以此进行SOH在线估计.其中电化学模型的准确性较高,但模型过于复杂,不适合应用到电池管理系统中;等效电路模型的观测器方法简单且适用于在线系统,但是估计精度不高,无法准确跟踪电池的老化状态.

如今,大数据技术快速发展,大量多维、实用的电池数据被收集,为基于数据驱动的方法提供了巨大潜力.数据驱动方法的基本思想是通过建立电池外部特性与SOH的非线性映射关系,避免考虑电池内部复杂的电化学反应.常用的模型[14-17]包括极限学习机(Extreme Learning Machine,ELM)、支持向量机(Support Vector Machine,SVM)、高斯过程回归(Gaussian Process Regression,GPR)和人工神经网络(Artificial Neural Network, ANN)等.除选择适合的模型外,健康因子(Health Factor, HF)提取也是实现SOH准确估计的关键.实际上,由于电池的电压、电流和温度等数据可直接从电池管理系统(Battery Management System, BMS)中轻易获得,所以BMS已被广泛用于特征提取.文献[18]中从电池完整的充电电压、电流和温度曲线中提取了4个HF,经过主成分分析(Principal Component Analysis,PCA)处理后作为GPR的输入来估计电池的SOH和剩余寿命(Remaining Useful Life,RUL),不仅精度较高且能给出估计值的不确定性表达,然而HF提取需要完整的充电数据,实际中难以获得.文献[19]中提出一种基于最小二乘SVM误差补偿模型,以等压升时间为模型的输入来动态补偿经验模型的预测结果.文献[20]中通过分析容量增量(Incremental Capacity,IC)曲线来确定与容量高相关性的电压片段进行HF提取,并使用计算量较小的核岭回归实现SOH在线估计.然而,在处理大量、多维的电池运行数据时,通过对数据进行二次特征分析来筛选出高质量数据片段更加重要.文献[21]中通过提取不同电压区间下的IC曲线峰值作为HF来估计SOH.文献[22]中从差分热伏安(Differential Thermal Voltammetry, DTV)曲线中提取峰值、峰位和谷值作为HF,使用改进的高斯回归建立起电池的老化模型.但是,这类方法直接从IC曲线或DTV曲线中进行HF提取,在微分计算误差和噪声干扰的影响时,会严重降低SOH估计的效率和准确率.综上可知,上述文献所用的神经网络和机器学习模型,其超参数一般需要人为调试或者利用智能算法寻优,导致计算成本较高且模型的泛用性能较差,而且在特征提取方面未综合考虑电压、电流和温度的共同影响.

针对以上问题,选择一种训练时间短、泛化能力强和计算效率高的ELM作为集成学习的子模型,提出一种基于融合HF和集成学习的锂离子电池SOH估计方法.首先,离线阶段收集电池的老化数据,通过定性分析电池的dQ/dV和dT/dV(Q、V和T分别为电池的充电容量、充电电压和充电温度)曲线从片段电压、电流和温度中提取与SOH相关度最高的数据区间作为HF.然后,进行主成分分析降维处理后输入到集成ELM(Integrated ELM,IELM)模型中得到N个SOH的估计值,经过可信度决策剔除其中不可信的输出,将剩余估计结果的均值作为最终SOH预测值.最后,使用NASA和牛津大学电池老化数据集中的多块电池进行实验验证,表明方法的准确性和可靠性.

1 健康因子构建

1.1 锂离子电池老化数据

数据来自NASA锂离子电池老化数据集[23]中编号B0005、B0006、B0007和B0018号电池数据和牛津大学电池老化数据集[24]中的8个电池(Cell 1～Cell 8)数据.NASA数据集中使用的LG Chem 18650圆柱形电池阴极为LiNiCo0.15Al0.05O2,阳极为石墨,额定容量为2 A·h.老化实验中对锂离子电池使用1.5 A的恒定电流充电至截止电压4.2 V,恒压阶段电流逐渐减少至截止电流20 mA,然后施加2 A的恒定电流放电至截止电压,在该模式下进行重复充放电.牛津大学锂离子电池老化数据集包含8块Kokam的钴酸锂离子软包电池,型号为SLPB533459H4,阴极为锂钴氧化物和锂镍钴氧化物,阳极为石墨,额定容量为740 mA·h.老化试验中反复对锂电池进行1.48 A恒流充电,其放电过程模拟Artemis市区行驶工况,每隔100次循环测量一次容量.本文SOH定义为当前最大可用容量与额定容量的比值,两个数据集的SOH变化曲线如图1所示,其中M为循环次数.

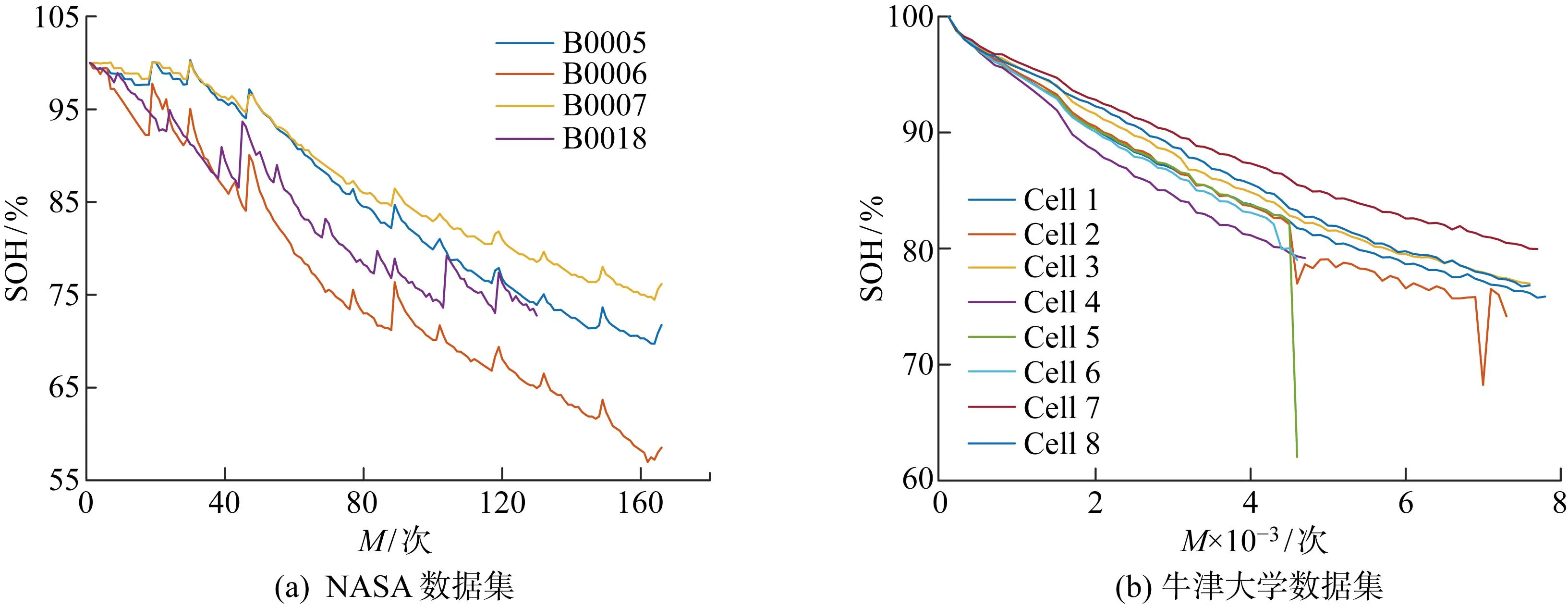
图1 NASA 数据集和牛津大学数据集锂离子电池的SOH曲线Fig.1 SOH curves of lithium-ion batteries from NASA datasets and Oxford University datasets

1.2 片段数据分析

实际上,电池的放电曲线随着工况的变化而变化,难以获取稳定的数据,而充电工况往往是固定的,可直接利用BMS监测并获取稳定的电压、电流和温度数据.图2(a)和2(b)显示出电池的充电电压和温度曲线由红到黑变化,代表电池的老化状态逐渐加重,其中t为时间.可以看出,随着电池老化加重,充电电压到达截止电压的时间越短,且充电时的温度逐渐升高,表明电压、温度与电池的SOH之间存在一定关联性.

因此,可以从电池充电电压和温度曲线中提取健康因子来表征电池的不同老化状态.考虑到大量输入数据会增加计算复杂度,且在电池的实际使用过程中采集的数据往往是片段的,为了降低估计模型对数据量的依赖性,通过离线分析dQ/dV和dT/dV曲线确定电压、温度与容量相关度都较高的数据区间,获取高质量的健康因子.此外,为了尽可能使原有电池老化信息显现出来,使用SG (Savitzky-Golay) 滤波法对dQ/dV和dT/dV曲线进行滤波处理,如图2(c)和2(d)所示.dQ/dV和dT/dV曲线通过B个采样点的有限差分获得,具体计算公式如下:

(1)

(2)

式中:Q(k)、V(k)和T(k)为第k次采样电池的充电容量、充电电压和充电温度.B值越大,越能降低噪声对曲线的影响,但过大可能会淹没曲线原有的峰值特性,因此经权衡将B值设定为10.

从图2(c)中的dQ/dV曲线可以看出,曲线的峰值位于3.95～4.05 V,代表该段电压区间与电池的容量之间存在高度关联性.温度与容量之间的潜在联系可以通过dQ/dT分析,表达式如下:

(3)

由式(3)可知,温度对容量关联程度与dQ/dV成正比,与dT/dV成反比.因此,由图2(c)和图2(d)可以发现,当电压在3.95～4.0 V时,dQ/dV恰好为峰值且dT/dV也处于0附近,使得dQ/dT最大.因此,可以针对该电压区间[V1,V2]内的充电数据提取特征,对此数据区间内电压对时间的积分作为HF1,温度对时间的积分作为HF2,电流对时间的积分作为HF3,具体计算公式如下:

(4)

(5)

(6)

式中:Vcc为恒流充电电压;t1到t2为Vcc从V1至V2所需时间;Tcc为电池恒流充电时的温度;I为恒流充电的电流;i为电池第i次循环.

1.3 健康因子相关性分析

通过前文对片段数据的定性分析,初步确定了与容量相关度较高的电压、电流和温度区间,为了定量找出具体的数据区间,采取Pearson和Spearman系数进行衡量,具体计算如下:

(7)

(8)

式中:X和Y为样本总体;xi和yi为样本个体.相关系数的值介于-1到+1之间,其绝对值越接近1,表示二者相关程度越高,当等于0时表示两者之间没有线性关系.

1.4 健康因子优化

提取的3个健康因子与SOH变化曲线如图3所示,可知健康因子相互之间存在趋势和波动重叠的部分,为了降低计算复杂度,利用主成分分析法将重叠信息与多余信息分离,在保留原有信息的同时,将原来的3个健康因子重组为一个新的向量记作间接健康因子(Indirect HF,IHF),具体步骤如下.

首先设X=[HF1HF2HF3],为n×m阶的矩阵,n为样本数,m为向量数,计算协方差矩阵:

(9)

式中:X*为标准化后的X.X*的特征向量ui和特征值λi(i=1, 2, …,k)由下式计算可得:

Sui=λiui

(10)

令U=[u1u2…uk],降维后的矩阵Z可由下式所得:

Z=X*×U

(11)

各主成分的贡献率可通过下式获得:

(12)

选择贡献度最大的主成分作为IHF进行SOH估计,使模型的输入矩阵阶数由n×m变为n×1,大大降低了模型的计算复杂度.

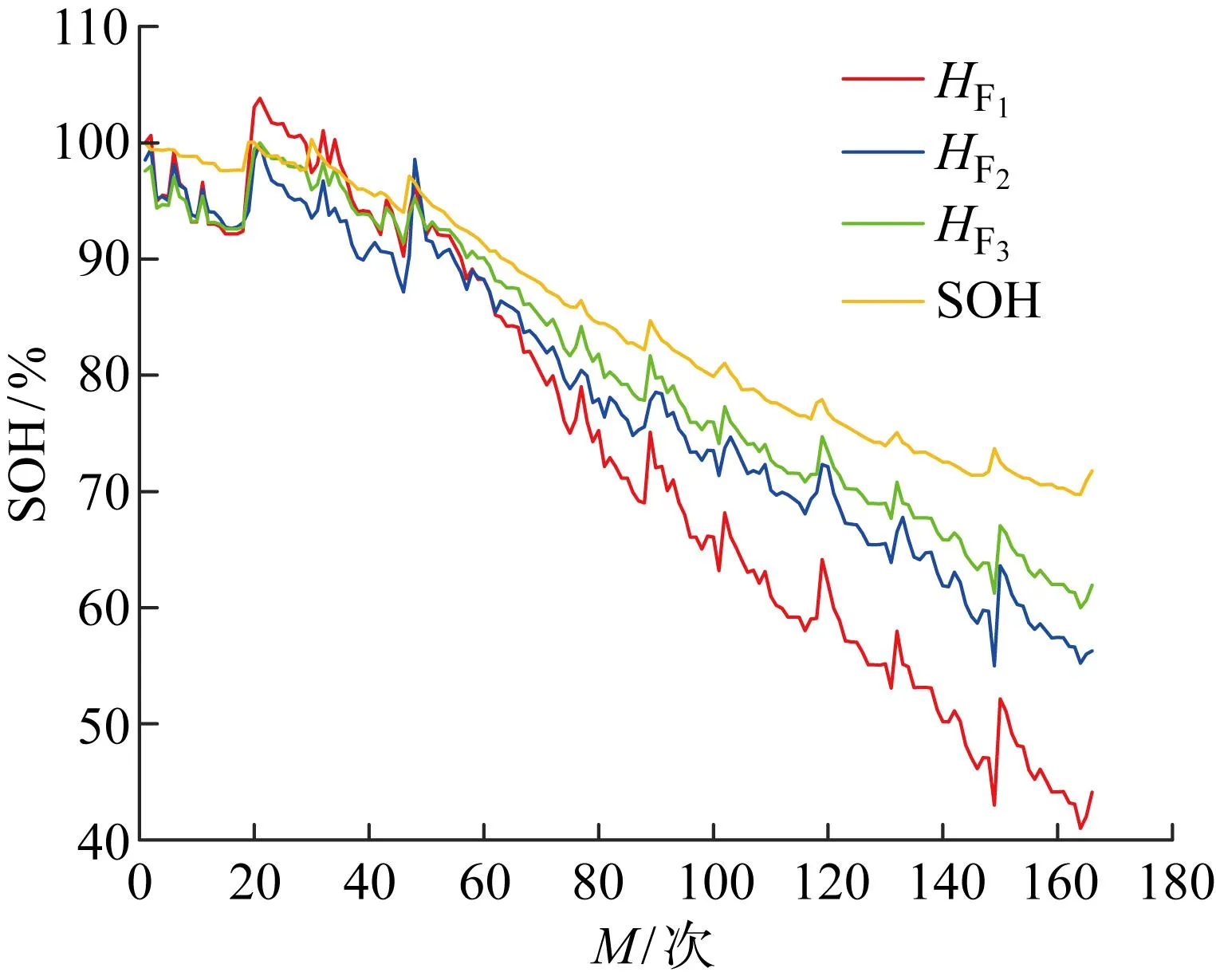
图3 B0005不同的HF与SOH的变化曲线Fig.3 Variation of different health factors with SOH of B0005

2 基于IELM的锂电池SOH估计 模型

2.1 ELM

ELM是Huang等[25]提出的一种单隐藏层前馈神经网络,其主要思想是随机分配输入层与隐藏层的连接权重wi和偏置bi,从而提高计算的延展性.与传统的机器学习,如SVM、相关向量机和GPR等相比,ELM的计算速度更快,泛化性能更好,实现更简单.

ELM的结构由输入层、隐藏层和输出层组成,如图4所示.假定给定的数据集{xi,yi|xi∈Rn,yj∈Rm,i=1, 2, …,L},yj代表输出,xi代表输入,L为隐藏节点数.对于单个ELM,其隐藏层输出的数学表达式如下:

图4 单个ELM的网络结构Fig.4 Structure of an ELM network

hi(x)=g(wix+bi),wi∈Rn,bi∈R

(13)

式中:hi(x)为第i个节点隐藏层的输出;g(·)为激活函数.由此可得单个ELM的输出为

(14)

式中:βi为第i个节点隐藏层到输出层之间的连接权重;H=[h1(x)h2(x) …hL(x)];β=[β1β2…βL]T.ELM学习过程的目标是通过矩阵求解的方法找到使误差最小的最优β.最优β的计算方法为

β*=H+Y

(15)

式中:H+为H的Moore-Penrose广义逆矩阵.如上所述,ELM的学习过程不同于传统神经网络训练算法需要对神经网络权重进行迭代调整.因此,其学习速度比传统机器模型快数倍,仅需要设置激活函数和隐藏层数目就能实现SOH估计,不需要过多人为干涉,并且所需的计算内存也很小.

2.2 集成学习模型

ELM因其本身学习速度快的特点,适合大规模的数据处理,然而ELM随机给定网络权重来进行学习的特点,使得单个ELM的输出结果并不稳定.为了提高准确性和可靠性,通过重复实验来减小误差,因此选择具有随机学习特性的ELM作为集成学习的子模型.

集成学习的基本框架如图5所示,将提取的IHF分别输入到N个ELM模型中,每个ELM单元的网络参数和隐藏层数均随机给定,由此可以得到N个SOH估计值.图6显示了B0005号电池经过200个ELM模型输出的SOH估计误差和分布,可以看出误差大致呈正态分布,其中MAE为平均绝对误差(Mean Absolute Error, MAE).虽然大多误差分布在 -0.5%～0.5%内,但尚有部分ELM输出误差较大.

图5 IELM的框架图Fig.5 Frame diagram of IELM

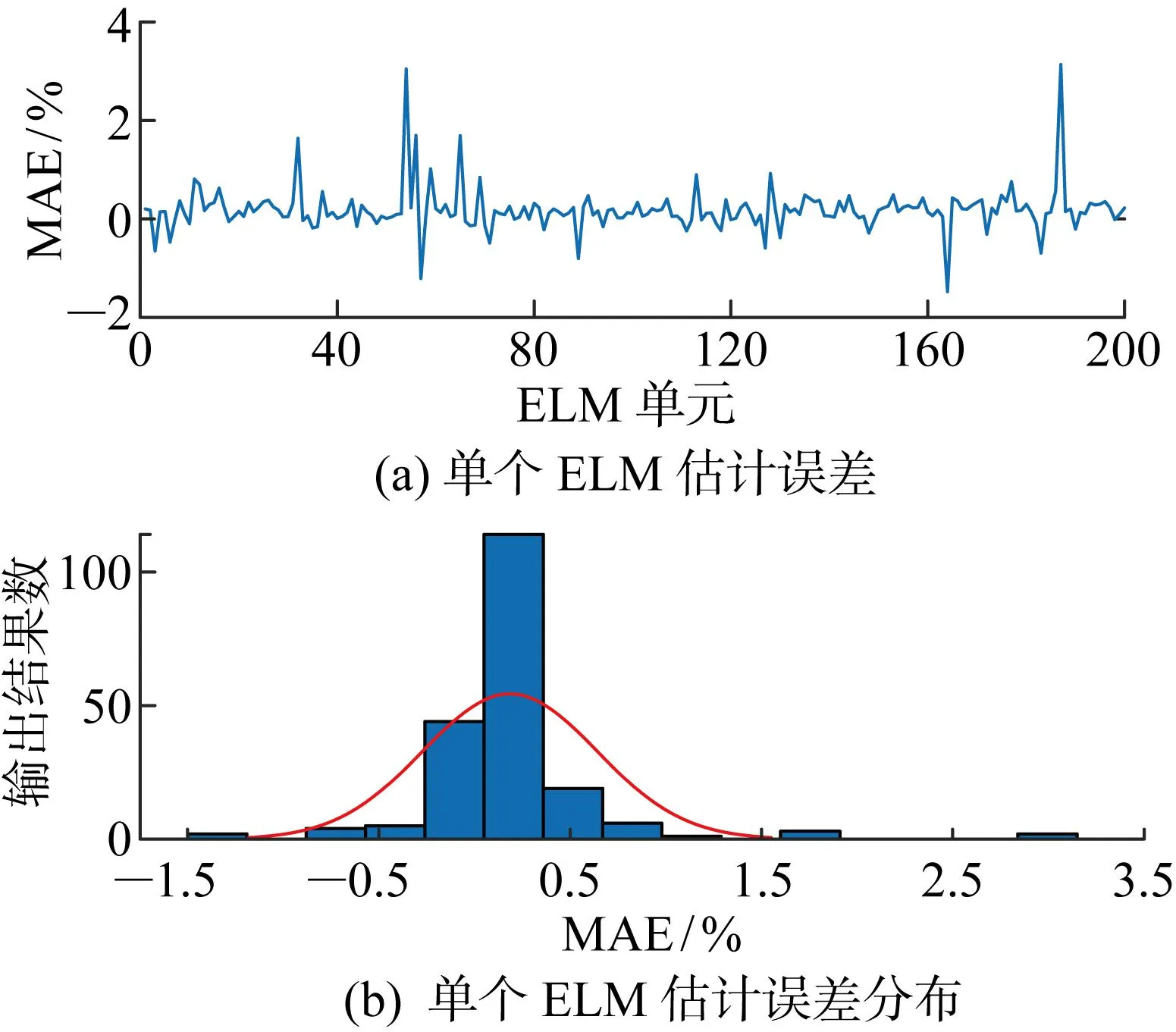
图6 B0005号电池的估计结果误差分析Fig.6 Error analysis of estimated results of B0005 battery

因此,根据拉依达准则设计一个可信度决策的策略来剔除“不可信”的ELM输出,仅使用“可信”的输出计算最终的SOH估计值.为减小异常值影响,使用样本中位数和标准差代替拉依达准则中的真实均值和方差:

(16)

(17)

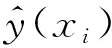
(18)

3 实验验证与分析

采取MAE、平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)、均方根误差(Root Mean Square Error, RMSE)评价模型性能,定义如下:

(19)

(20)

(21)

3.1 IHF与电池SOH相关性分析

采取遍历法对前文确定的数据区间进行邻域搜索,在权衡数据量长度和相关性强度后,得到NASA数据集B0005、B0006、B0007和B0018电池特征提取所需数据区间为3.98～4.0 V电压变化内的数据,牛津大学数据集中Cell 1～Cell 8号电池特征提取所需数据区间为3.8～3.85 V电压变化内的数据.

对此区间内电压、电流和温度进行特征提取得到3个HF值,然后使用PCA进行降维处理得到IHF.为定量衡量本文所构建的IHF与电池SOH之间的相关性强弱,选择Pearson系数和Spearman系数进行评价,计算结果如表1所示.结果可知,本文所构建的HF在两个数据集中均大于0.9,且提取特征所需要的数据长度仅为20、50 mV,在实际应用中可较易获得.

表1 IHF与各电池SOH相关性分析

3.2 集成学习模型预测结果

实验在CPU型号为i5-7300HQ、RAM内存为16 GB、显卡为GTX1050Ti的计算机设备上进行.为验证方法的准确性,每次选择NASA或牛津大学电池老化数据集中的一块电池作为测试集,剩余电池数据则作为训练集.以NASA数据集为例,当B0005作为验证集时,B0006、B0007和B0018则作为训练集;当B0006作为验证集时,B0005、B0007和B0018则作为训练集,以此类推.同时考虑实际的计算成本和模型预测精度要求,当集成模型ELM为200个时,就可达到稳定的估计输出.各电池的SOH预测结果和误差如图7和8所示,图中红色曲线代表预测值,蓝色曲线代表SOH真实值;误差指标计算结果如表2所示.

图7 牛津数据集SOH估计结果Fig.7 SOH estimation results from Oxford dataset

从预测曲线中可以看出,本文方法不仅能够准确估计电池的线性老化趋势,而且对局部的波动部分也能准确跟踪.从误差结果可知,NASA数据集中的预测误差除了个别点在4%左右,大部分误差均在2%以内;牛津大学数据集中仅有少数点误差在3%左右,绝大部分位于1%以内.

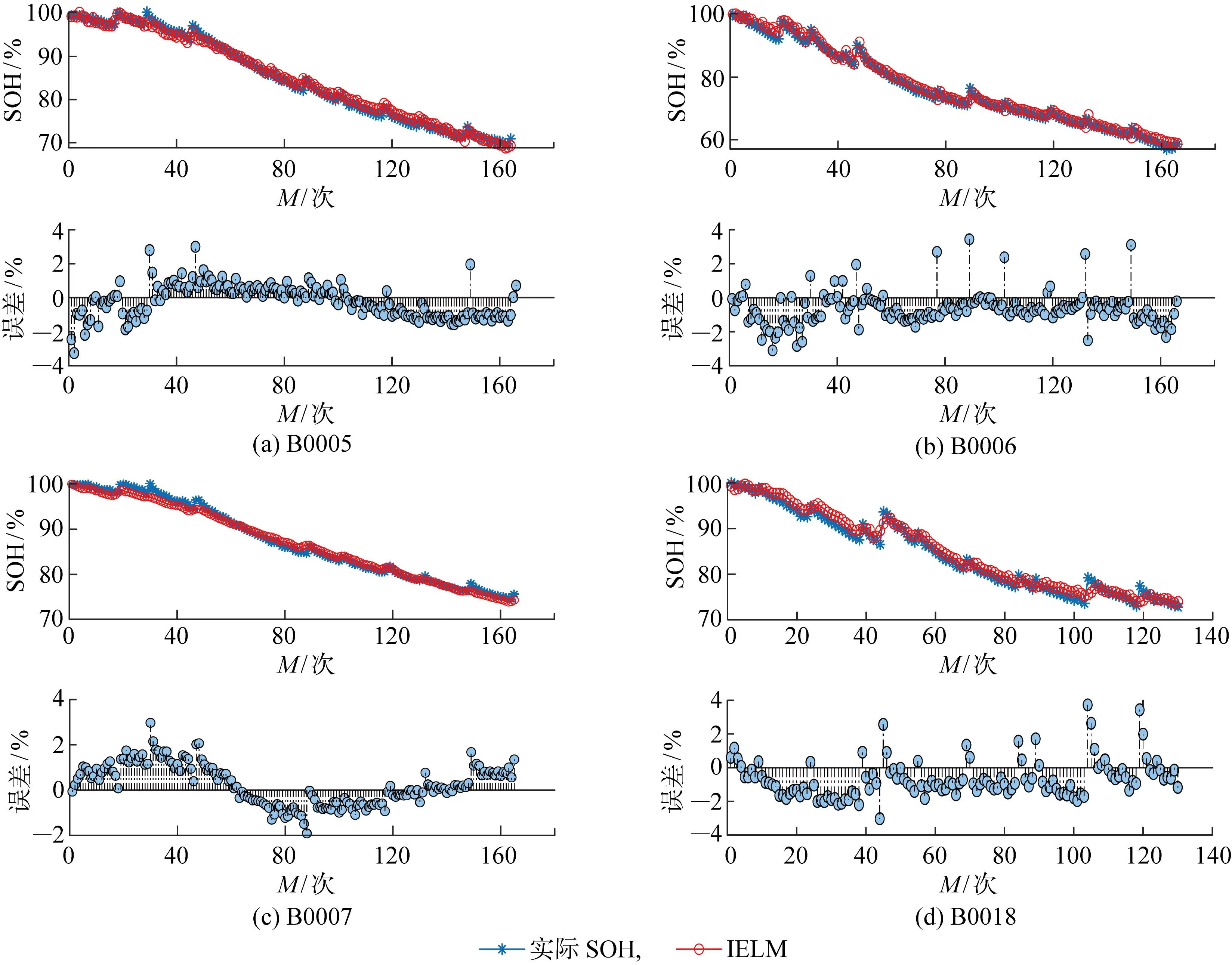
图8 NASA数据集SOH估计结果Fig.8 SOH estimation results from NASA dataset

实际上,当电池的SOH低于70%时,健康特征与SOH之间的关系非线性程度加剧会引起误差增大.因此,当电池容量衰减为额定容量的70%～80%时,电池的性能将呈指数级下降,应及时更换电池,一般将该阈值称为寿命终止阈值.实际运行中很少会获得低于该阈值的数据,故可以接受较大的估计误差.由表2可知,NASA数据集的SOH估计误差指标均处于2%以内,牛津大学数据集的SOH估计误差指标均处于1%以内,尽管每块电池的老化条件各不相同,但本文所构建的健康特征和模型对每块电池都能达到较好的预测结果,表明方法有较强的可靠性和准确性.

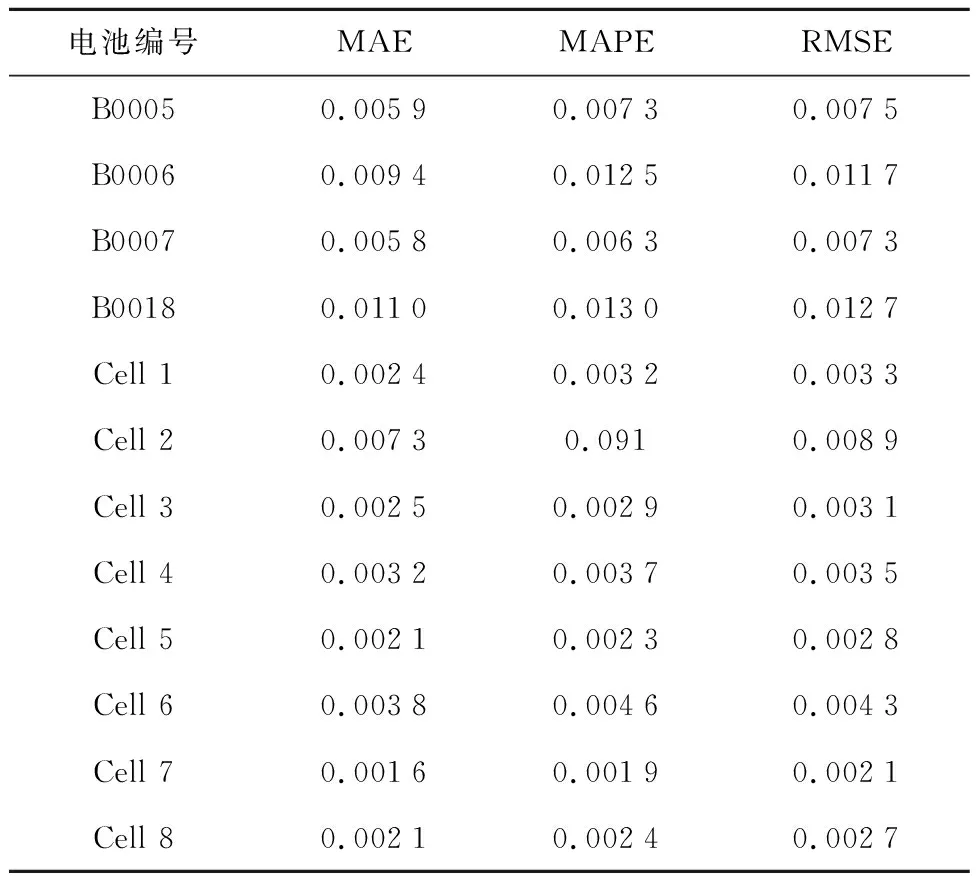
表2 各电池SOH估计结果的误差指标Tab.2 Error index of SOH estimation results of each battery

为验证本文特征选取方法(M1)对电池SOH估计的准确性,基于不同情况设计以下特征选取方案:M2为从电压提取的健康特征;M3为从电压和电流中提取的健康特征;M4为从电压和温度中提取的健康特征.从表3可以看出,由于同时考虑了电池电压、电流和温度因素,M1方法能更好地追踪电池老化状态,所以模型的估计误差最低.在实际情况中,若因某一传感器故障不能使用M1进行特征提取,而使用其余特征提取的方法,其估计误差可维持在2%以内,也能实现较好的SOH预测,对实际工况有指导意义.

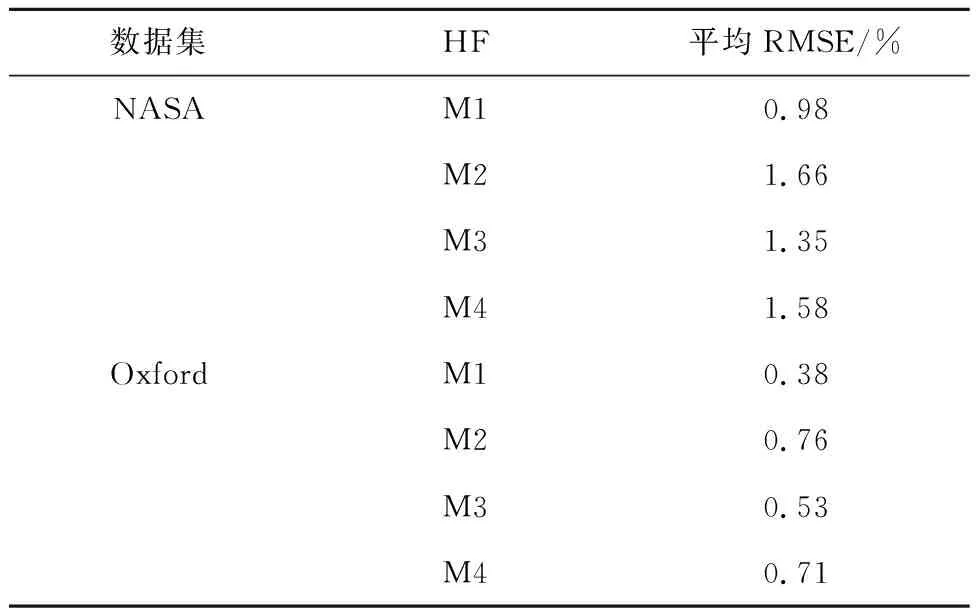
表3 不同健康因子下的SOH估计误差Tab.3 SOH estimation error at different health factors

此外,为了验证模型的性能,选择与当下主流的SOH估计模型进行比较,如ELM、长短期记忆(Long Short-Term Memory, LSTM)神经网络和GPR模型,所有算法使用相同的训练集和测试集,且测试平台相同,估计结果和模型运行时间如表4所示.可知,IELM模型在两个数据集上的平均RMSE最低,且计算速度比LSTM快,与GPR相当.然而,LSTM和GPR需要提前设定好模型的超参数,其参数的寻优过程往往比较繁琐,相比之下ELM和IELM模型因其本身特性无需进行参数设置,能够节省大量的额外时间.但单一的ELM存在输出不稳定的情况,IELM模型则通过集成学习和可信度原则对原本单一模型进行了改进,使得模型在两个数据集上的平均RMSE分别降低了0.78%和0.3%.实验结果表明,本文方法与其他主流模型相比有较高的精度和可靠性.

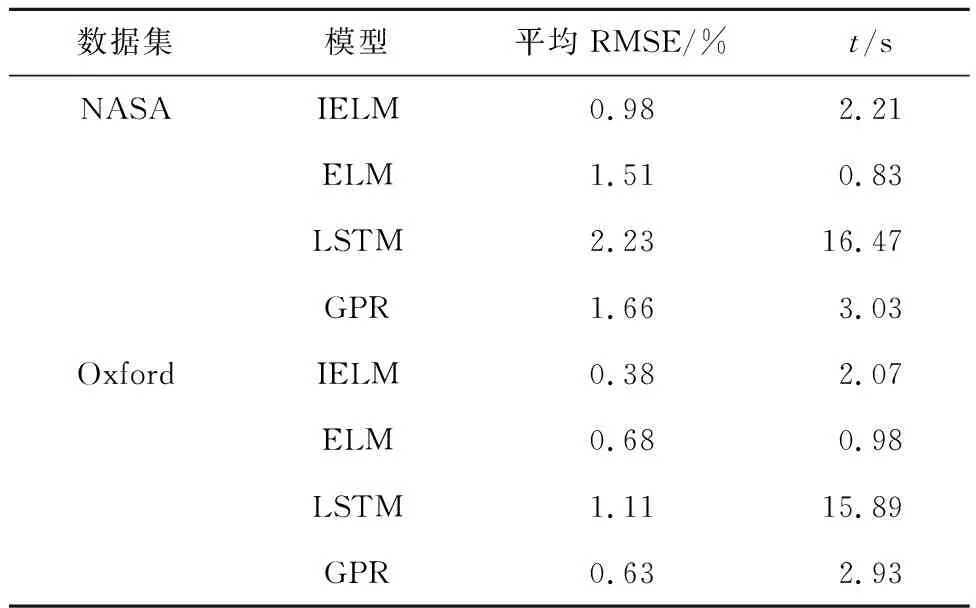
表4 不同模型的估计误差和计算速度

4 结语

提出一种基于融合HF和IELM模型的锂离子电池SOH在线估计方法.通过分析dQ/dV和dT/dV曲线,选择电压、温度和容量三者相关性较高的数据区间进行特征提取,然后进行PCA处理后作为集成模型的输入.选择具有随机学习特点的ELM作为集成学习的子模型,并通过一个可靠的可信度决策规则剔除偏差较大的估计结果.最后,使用NASA和牛津大学电池老化数据集共12块电池对所提方法进行多电池实验验证,结果显示本文方法能够在较短时间内从20、50 mV电压片段所包含充电数据区间内提取健康特征并准确估计出电池的SOH,结果表明该方法具有较高的准确性和可靠性.