铰接支撑双重抗侧框架及其弹塑性抗侧性能研究

余玉洁，韦权飞，王霄翔，胡婉颖

铰接支撑双重抗侧框架及其弹塑性抗侧性能研究

余玉洁1，韦权飞1，王霄翔2, 3，胡婉颖1

(1. 中南大学土木工程学院，长沙 410075；2. 湖南建设投资集团有限责任公司，长沙 410004；3.湖南建工集团有限公司，长沙 410004)

基于现有分层装配柔性支撑框架，提出改进的铰接支撑双重抗震改进型轻钢框架体系．外墙转角或边墙处采用贯通式边柱，结构内部采用柱分层、梁贯通式结构设计．内部分层立柱之间设置柔性交叉支撑提供结构的初始抗侧刚度，贯通式边柱与水平贯通梁刚性或半刚性连接形成外围框架，提供后继抗侧储备并形成第2道抗侧防线．采用理论分析方法得到改进型框架梁、柱、支撑等构件初步设计方法，并基于Pushover分析改进型框架弹塑性抗侧承载性能和关键结构参数影响规律．该结构传力机制清晰，具备多重抗侧承载机制，并可基于结构力学方法有效得到结构设计准则．柔性支撑在距边柱一定距离后其位置变化不影响结构抗侧承载性能．内部分层立柱节点刚度对结构抗侧性能影响较小，实际设计中可采用全螺栓连接或限位铰接．边框梁柱连接刚度将影响外围框架刚度和结构失效机制，实际设计中宜采用加劲型螺栓连接以保证有足够的抗弯刚度．体系中各节点均可在保障结构性能条件下采用螺栓连接以实现全装配化建造．

铰接支撑双重抗侧框架；装配化建造；抗侧性能；受力分析；Pushover分析

近年来，随着国家双碳战略和建筑业转型升级的持续推进，装配式钢结构住宅得到快速发展[1]．住宅类民用建筑与公建不同，其建筑内部为满足居住功能常常具有多样、复杂的平面局部，柱网不规则且柱距较小．因此钢结构住宅结构设计中需要重点考虑居住功能多变的建筑需求[2]．受此限制，低多层钢结构住宅中常采用冷弯薄壁结构体系[3-4]或小尺寸截面的钢框架结构体系．周绪红等[5]提出了冷弯薄壁型钢-钢板剪力墙体系，推广冷弯体系应用于多层住宅．管宇等[6]、石宇等[7]、叶露等[8]通过系列试验及模拟完善其中冷弯薄壁组合楼盖、剪力墙等关键构件以及整体结构抗震性能和设计方法．叶继红[9]、Wang等[10]提出多层轻钢龙骨式复合剪力墙结构体系，采用双拼或三拼的C型龙骨承重，并在关键位置引入方钢管轻质混凝土柱增大竖向承重和抗震能力．也有学者探索轻型框架体系的改进研发[11]，如曹万林等[12]研发了轻钢组合框架-轻型填充墙板结构体系，并进一步优化提出了装配式轻钢龙骨组合墙以满足住宅的户型变化需求．

对于低多层钢结构住宅，同济大学王伟等[13]参考日本的全装配式住宅研发了分层装配柔性支撑框架结构体系，采用梁通长、柱分层装配，并结合柔性支撑的方式组合而成．该体系可实现全工业化制作和装配安装，具有施工周期短、设计便捷、综合效益好等优点，且可基于住宅需求实现结构灵活调整．通过节点、支撑单元以及支撑框架整体的系列试验研究证明该结构体系有较好的抗震性能[14]．但该体系本质上仍主要依靠柱间交叉柔性支撑抵抗水平力，一旦支撑破断其抗侧性能将大幅下降[15]．与此同时，我国《建筑抗震设计规范》(GB 50011—2010)[16]对于大部分地区工程结构都要求具有多重抗震防线，从而避免大震作用下因部分结构或构件破坏而导致整个结构倒塌．

本文在分层装配柔性支撑框架基础上进行改进，提出了铰接支撑双重抗震轻钢框架结构体系．采用理论推导和典型框架抗侧性能分析得到改进体系的设计策略和抗侧性能影响因素．研究成果可为低多层钢结构住宅体系研发和设计提供参考．

1 铰接支撑双重抗侧框架结构体系

分层装配柔性支撑框架结构体系特点在于采用梁贯通、柱分层并通过端板螺栓连接组合形成基本框架，柱间采用交叉柔性支撑抵抗水平力．但一旦支撑失效，其结构抗侧性能将大幅下降．针对以上不足，综合考虑住宅建筑中内外墙体布局特点和结构抗震需求，提出改进的铰接支撑双重抗侧框架结构体系，如图1(a)所示．

结构中位于外墙转角或边墙处立柱仍采用柱贯通式型钢柱或钢管混凝土柱，边框梁柱连接处采用栓焊混合或端板螺栓连接的刚性或半刚性节点；在房屋内侧采用分层装配式结构中柱分层、梁贯通式结构设计；结构内部采用小尺寸钢管立柱，在各层内与上下水平贯通梁之间采用可拆卸的螺栓连接(图1(b))；沿用分层装配式体系中构造，立柱之间设置扁钢制作的铰接柔性交叉支撑以提供结构抗侧，扁钢中部设置花篮螺栓张紧．

该结构体系中内部分层立柱主要承受竖向荷载，可采用小截面构件，在满足竖向承重受力下实现结构柱藏于墙体内的使用要求．外围贯通式钢管混凝土柱或钢框柱位于外墙位置，对室内空间布局影响较小．在正常使用、小震及中震时主要通过内部柔性支撑提供结构的抗侧和抗震能力．同时外围贯通式框柱及框架节点可提供结构抗侧和抗震性能储备，在大震作用下或铰接支撑框架发生破坏后作为第2道抗震防线．此外，内部立柱和柔性支撑藏于墙内且可拆卸装配，可在保障整体结构受力性能条件下根据房屋内部功能布局需求进行位置调整．

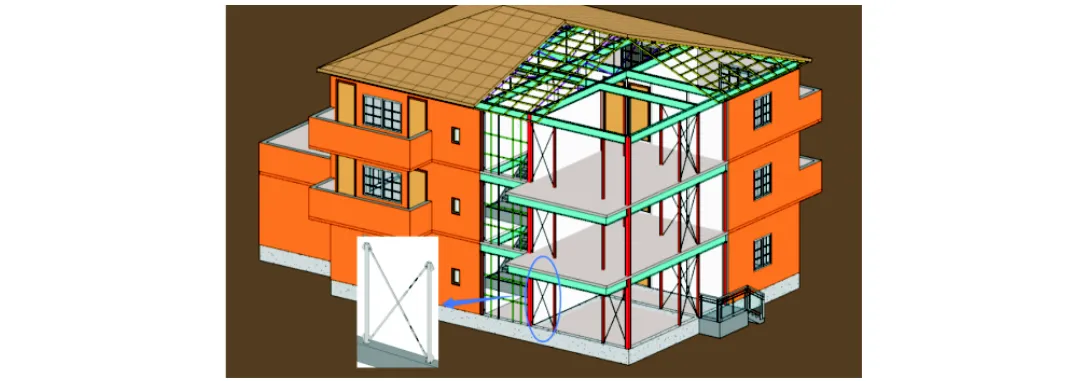
（a）结构体系构成

（b）铰接立柱及铰接支撑节点构造

图1 铰接支撑双重抗侧框架结构体系

Fig.1 System diagram of the hinged-brace dual-resistance frame

2 铰接支撑双重抗侧框架受力分析

铰接支撑双重抗侧框架在结构设计中，其内部分层立柱端假定为铰接，在静荷载时主要通过铰接柔性支撑提供抗侧能力，外围框架提供多重抗侧储备．因此理想的结构受力和失效顺序为：随着侧向水平荷载的增大，柔性铰接支撑为主要抗侧刚度来源，并最先发生屈服，之后外围框架提供后备抗侧能力；基于钢框架“强柱弱梁”理念，钢框梁端先于柱肢达到抗弯极限出现塑性铰，外围框柱作为最后一道抗震防线．因此在结构设计中应合理设计柔性支撑、外围框柱和水平贯通梁的截面尺寸和强度，以实现期望的结构受力过程．

2.1 铰接支撑双重抗侧框架受力关系计算

2.1.1 复合框架抗侧性能计算

图2(a)所示为代表性铰接支撑框架计和变形关系．交叉支撑铰接于立柱端部，仅在铰接节点处传递水平抗力．因此根据承载顺序和变形关系可将该框架划分为柔性支撑和复合框架两部分．图2(b)所示为复合框架计算简图，内部分层立柱通过螺栓固定并主要传递竖向荷载，忽略其抗弯承载能力，因此结构分析中可简化为两端铰接杆．外围框架采用刚性或半刚性螺栓连接，梁柱节点具备抗弯承载能力，在结构理论分析时可简化为刚接．

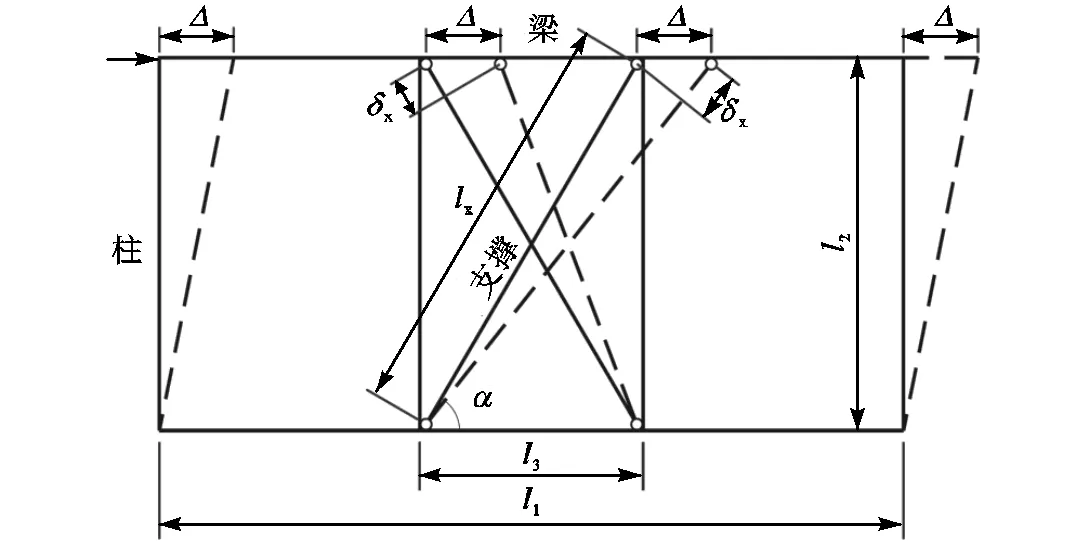
（a）结构变形几何关系

（b）复合框架计算简图

图2 结构计算简图

Fig.2 Schematic diagram of the calculation

复合框架在承受水平荷载时梁柱的受力状态可通过结构力学方法求解，得到框架发生水平侧移时框架梁端弯矩1和柱端弯矩2．假定框架贯通梁长度为1，抗弯刚度为1，边柱长度为2，抗弯刚度2，内侧一对铰接立柱居中设置，间距为3．框架顶端发生水平位移为．

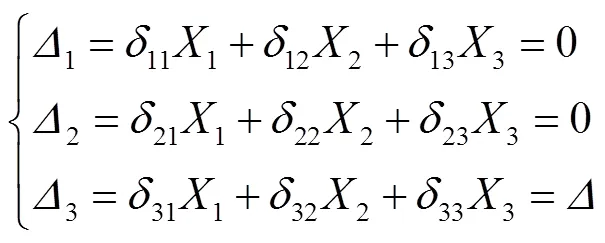
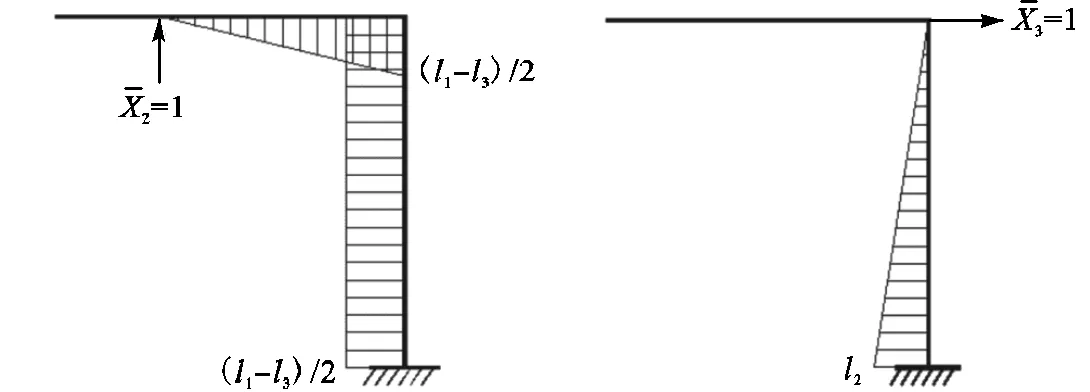
图3 力法求解图示

Fig.3 Diagram of the force method calculation

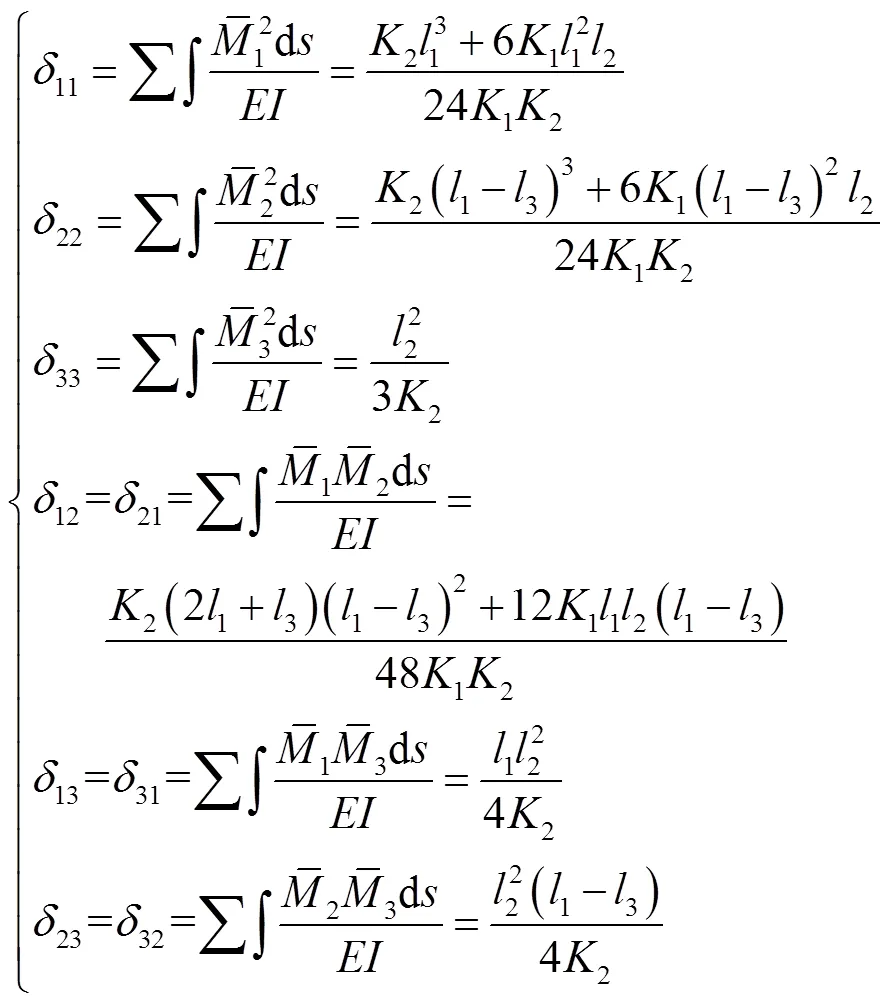
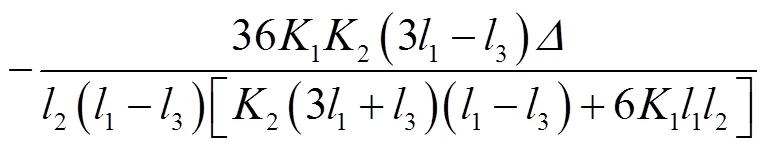
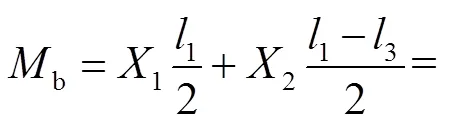
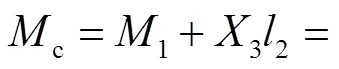
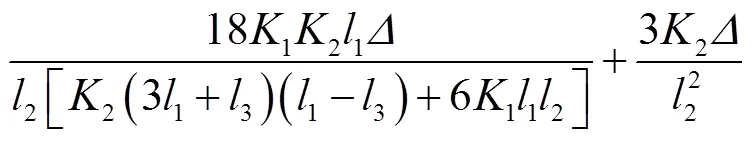
2.1.2 矩形钢管混凝土柱压弯承载强度计算

改进型框架在承受水平荷载时会在边柱产生拉压的竖向反力，因此受压侧边柱则处于压弯状态．将铰接支撑双重抗侧框架应用于多层住宅或办公楼时，其边柱为控制构件尺寸，可采用钢管混凝土边柱构造．因此在改进框架的失效状态判断时需要考虑到钢管混凝土边柱在压弯受力下的承载力大小．

对于钢管混凝土构件的承载力的计算方法，国内外学者多年来都开展了深入细致的研究工作，已有成套计算方法．矩形钢管混凝土柱压弯承载力强度，可通过极限状态理论进行计算．

矩形钢管混凝土柱压弯承载力可基于全截面压弯共同作用下全截面进入塑性时的极限平衡状态推导出钢管混凝土压弯构件轴力和弯矩的相关公式[17]．规范中为简化计算采用偏安全的直线相关关系，即

矩形钢管混凝土轴压承载力可基于叠加原理[18]进行计算，即

矩形钢管混凝土柱抗弯承载力也基于极限状态理论进行计算．假定矩形钢管混凝土柱达到弯曲极限时，钢管和受压区混凝土分别达到屈服和抗压强度极限，受拉区混凝土退出工作，如图4所示．

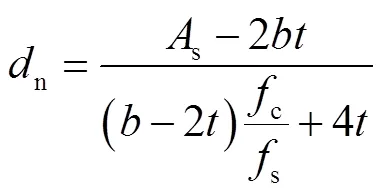
式中为钢管截面高度．

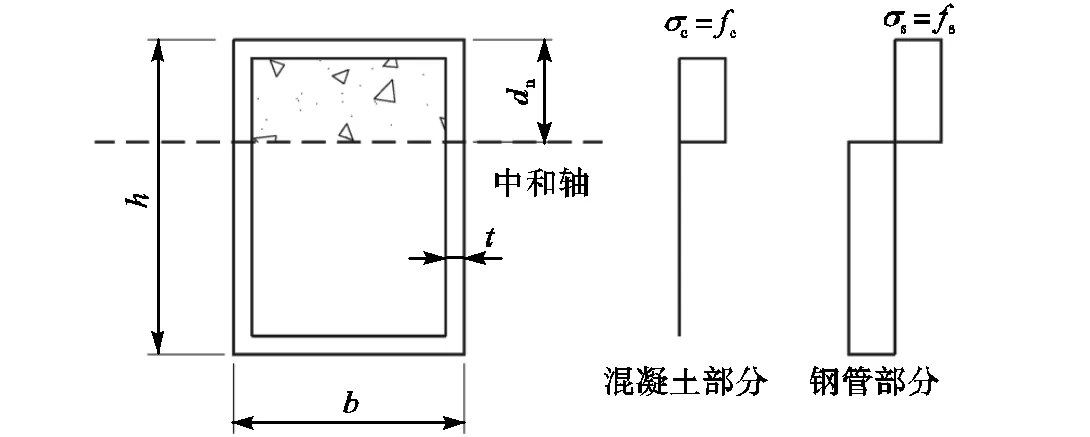
图4 截面受力计算简图

2.1.3 铰接支撑双重抗侧框架屈服机制

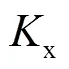
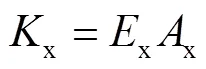
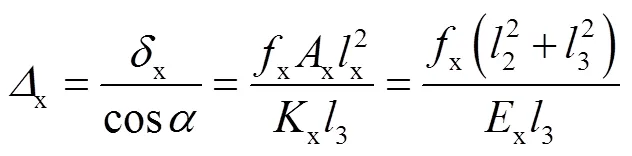
由式(4)～(6)可知，弹性状态内边框柱和水平贯通梁的弯矩和轴力大小均与水平侧移呈线性关系，因此可基于贯通梁和边框柱截面强度得到构件屈服或形成塑性铰时所需要的水平侧移大小．

当水平贯通梁采用H型钢梁时，其中水平梁刚度和截面抗弯承载力分别为

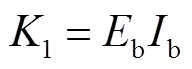
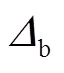
当边框柱采用钢管混凝土柱时，其抗弯刚度为

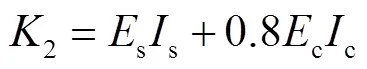
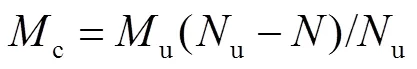
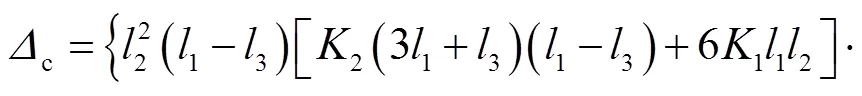
2.2 铰接支撑双重抗侧框架Pushover模拟验证

首先建立复合框架模型，验证力法推导的准确性和性能影响因素．采用结构力学方法进行抗侧性能推导时梁柱构件均仅考虑其抗弯刚度，并未考虑构件抗拉和剪切刚度影响．因此在复合框架抗侧分析中考虑理想抗弯杆件模式和真实杆件模式．理想抗弯杆件模式的Midas分析中，人为调整构件抗拉刚度和剪切刚度截面刚度放大系数实现其无穷大，而抗弯刚度能保持其实际大小，以实现杆件性能与理论推导一致．真实杆件模式中梁柱杆件的抗弯刚度、抗拉刚度和剪切刚度均为实际大小．开展典型框架的Pushover分析，计算在推覆位移＝15mm时梁柱构件的受力大小．复合框架理论计算与Midas结果对比如表1所示．

（a）复合框架模型 （b）铰接支撑双重抗侧框架

图5 改进型框架的Midas模型(单位：mm)

Fig.5 Midas models of the improved frame structures(unit：mm)

表1 复合框架理论计算与Midas结果对比

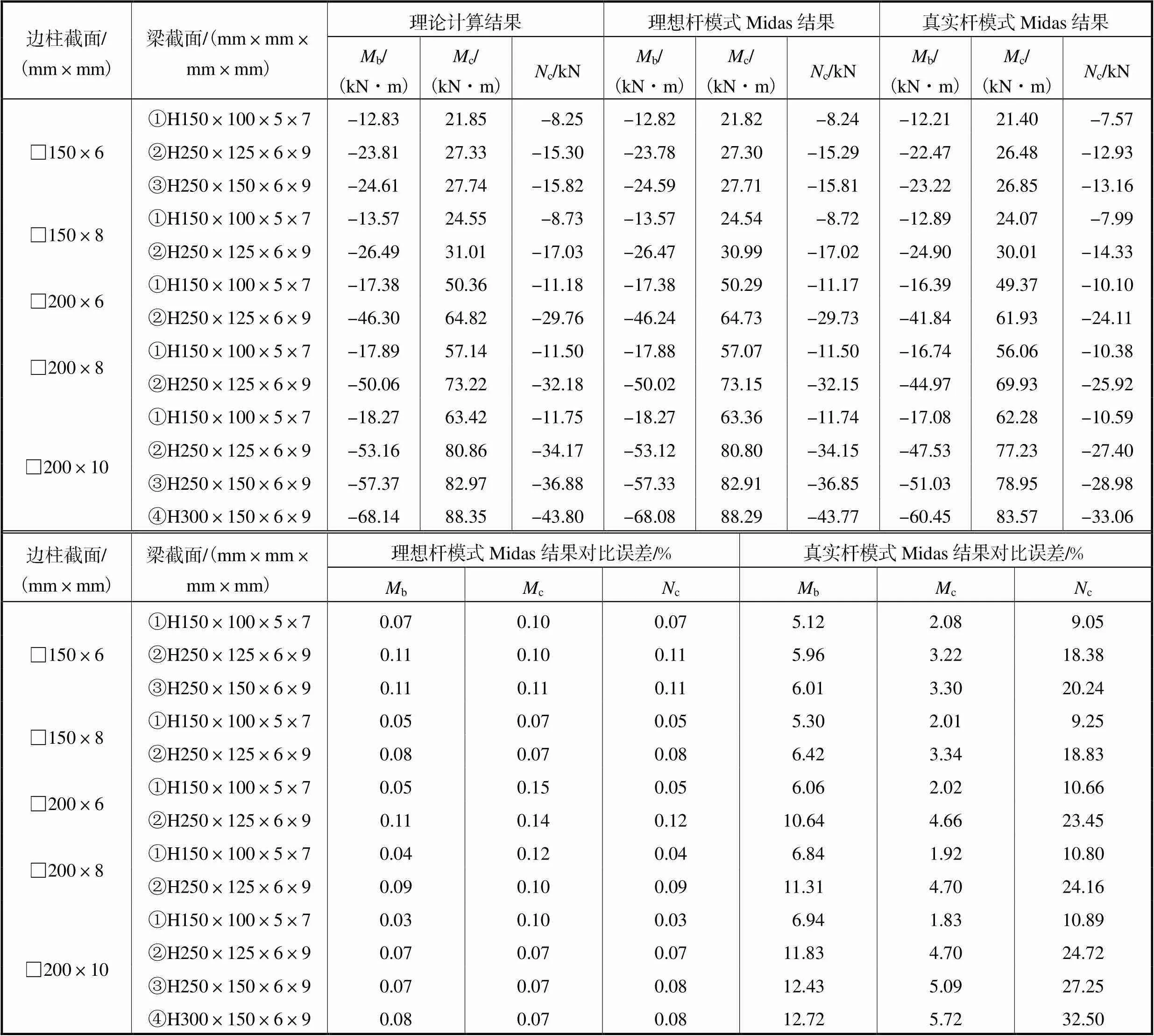
Tab.1 Comparisons between the theoretical calculations and the Midas results

框架中构件的屈服和塑性通过定义塑性铰模拟．对柔性支撑定义轴力铰，水平贯通梁定义弯矩铰，钢管立柱和钢管混凝土边柱定义轴力弯矩PMM相关铰，如图5所示．在定义塑性铰时，为使Pushover曲线能够出现下降段，模拟结构构件屈服后框架抗侧承载力变化及下降状态，梁、柱构件的弯矩-转角关系采用FEMA骨架曲线定义，使用软件默认的铰属性运算分析．图6所示为FEMA铰的骨架曲线特性．

图6 FEMA铰的骨架曲线特性

表2所示为分别采用理论分析方法和Midas中Pushover分析所得到的结构屈服顺序结果和对比．可见理论分析方法所得出的支撑、梁和钢管混凝土柱屈服顺序的结果与Midas一致，因此在结构初始设计阶段可采用理论分析方法进行框架中梁、柱杆件选型和设计，以实现预期承载机制和顺序屈服模式．

2.3 铰接支撑双重抗侧框架弹塑性抗侧承载机制

从表2中选择两个代表性工况分析铰接支撑双重抗侧框架的弹塑性承载和失效过程．两个工况中框架边柱均采用200mm×10mm的钢管混凝土柱，中部铰接分层柱采用100mm×5mm空心方钢管，柔性支撑采用宽40mm、厚5mm的钢板条．工况1中水平贯通梁采用150mm×100mm×5mm×7mm的H型钢，可实现支撑→梁端→柱端的理论屈服顺序．工况2水平贯通梁采用300mm×150mm×6mm×9mm的H型钢，其组成框架的理论屈服顺序为支撑→柱端→梁端．为得到框架弹塑性承载和失效全过程，Pushover分析中计算到最大节点水平侧移达到120mm，即达到4%的层间位移角变形．计算完成后提取基底剪力-侧移曲线以分析构件不同屈服和构件失效模式．

表2 结构构件屈服时的位移

Tab.2 Displacement of a structural member at yield

图7所示为工况1：理想屈服顺序工况，理论分析具有支撑→梁端→柱端的屈服顺序．在水平侧移逐渐增大时，支撑受拉先发生屈服，基底剪力-位移曲线出现第1个拐点；随后外围框架继续承载，直至梁端左右梁端屈服，承载曲线产生第2个拐点；梁端屈服导致承载力曲线刚度轻微下降，表明其对结构刚度影响不大．当钢管混凝土边柱柱脚屈服时产生第3个拐点，结构刚度明显降低；之后主要由钢管混凝土边柱提供主要抗侧能力，直至一侧边柱达到极限强度时，承载力曲线突然下降．

图8中工况2(非理想屈服顺序工况)采用强梁设计，基于理论分析其柱脚将先于梁端进入塑性．由推覆分析结果可见，当柱脚发生屈服时，框架承载力曲线刚度明显下降，随后梁端达到屈服，框架进入塑性承载阶段．当柱脚达到极限强度失效时，将使得框架承载力突然下降．相较于工况1，工况2框架的抗侧刚度变化幅度较大，达到失效前的侧移变形能力偏小，延性较低．

图7 理想屈服顺序工况

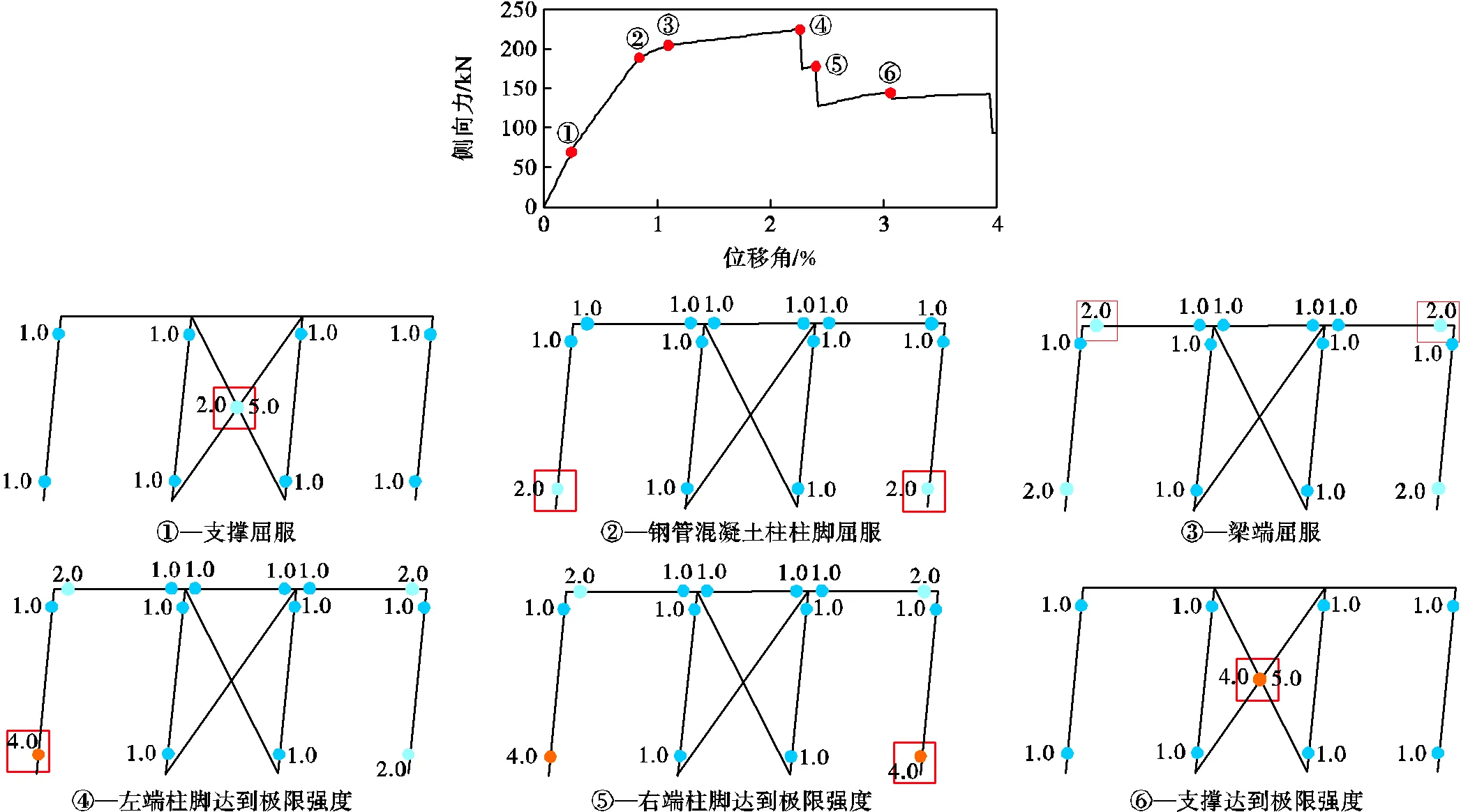
图8 非理想屈服顺序工况

3 改进型框架构造参数影响分析

改进型框架实际设计中内部分层立柱与水平贯通梁通过螺栓连接，水平贯通梁与框架边柱可采用焊接或加强型栓接节点，或采用栓接形成半刚性节点．而理论计算方法中节点处均进行了简化，即边框梁柱节点简化为刚接，分层柱与贯通梁节点简化为铰接，并且铰接支撑假定居中设置．但实际结构中，不同构造方式的螺栓连接均会产生一定节点抗弯刚度，并且柔性支撑位置也会随着建筑功能和墙体开洞需求而变化．这类构造参数和节点刚度对于结构抗侧性能的影响规律可采用不同构造参数下的Pushover模拟进行研究．

参数化分析中选择符合预期屈服顺序梁、柱设计构造组合，即框架边柱均采用200mm×10mm的钢管混凝土柱，水平贯通梁采用150mm×100mm×5mm×7mm的H型钢，中部分层立柱采用100mm×5mm空心方钢管，柔性支撑采用宽40mm、厚5mm的钢板条，支撑宽度为1.8m．分别变化支撑位置、分层立柱与水平贯通梁连接节点刚度、边框梁柱节点刚度开展参数化分析．

3.1 柔性支撑位置

通过改变交叉支撑与钢管混凝土边柱之间的距离实现柔性支撑不同设置位置的变化，分别模拟支撑距边柱2.1m、1.8m、1.5m、0.9m工况，如图9所示．所有模型中分层立柱与水平贯通梁连接节点为铰接，边框梁柱节点为刚接．分析并对比所得到的基底剪力-侧移关系曲线和失效模式，如图10所示．

（a）工况A：支撑距边柱2.1m  （b）工况B：支撑距边柱1.8m

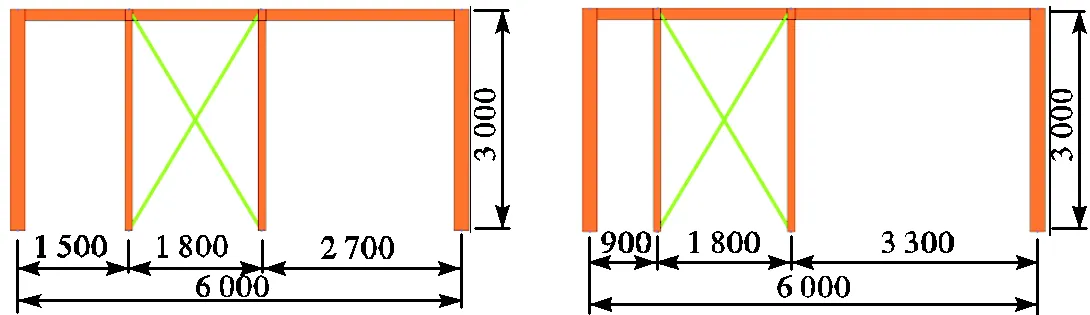
（c）工况C：支撑距边柱1.5m  （d）工况D：支撑距边柱0.9m

图9 支撑位置

Fig.9 Brace locations

（a）基底剪力-侧移曲线

（b）支撑距边柱0.9m(工况D)失效模式

图10 支撑位置影响

Fig.10 Influences of the brace locations

可以看出，当其他条件相同、只改变支撑距离两端钢管混凝土柱位置时，支撑距边柱2.1m、1.8m和1.5m工况的基底剪力-侧移曲线基本相同，且失效过程均与图7中屈服顺序和失效模式一致．说明支撑距边柱一定距离时，改变支撑位置对整个框架的弹塑性承载和失效过程影响较小．但当支撑距边柱过近时，其基底剪力-侧移曲线变化较大．当支撑距边柱较近时，框架初始弹性刚度下降，抗侧承载力水平降低．

图10(b)中给出工况D下关键构件出铰位置及变化顺序(图中红框标注)．随着水平侧移逐渐增大，受拉支撑先发生屈服．随后梁左端先于梁右端发生屈服．这与图7中失效模式有所差异，原因在于此时左端梁段线刚度较大，相同转动幅度下梁端弯矩更大先达到屈服，但此时承载刚度未明显下降．随着侧移的不断加载，左端梁相较于右端梁段先达到塑性铰失效．当梁右端及钢管混凝土柱柱脚屈服时，抗侧承载力下降，较未屈服前承载力下降82.3%．因此设计时交叉支撑不宜距离边框过近，距边框柱一定范围内，支撑位置可依据建筑及功能需求灵活调整而不影响结构的抗侧性能．

3.2 分层立柱连接节点刚度

框架内部的分层立柱与水平贯通梁节点在初设阶段可简化为铰接节点，但实际连接中可通过端板及螺栓与水平贯通梁翼缘连接，为半刚性节点，如图1(b)所示．为分析该节点影响，可在Midas中通过释放分层立柱端部约束刚度的方式，模拟节点的不同刚度水平．分别模拟了刚接、75%刚度、50%刚度、25%刚度和铰接5种工况(图11中工况a～e)．该分析中所有模型柔性支撑均居中设置，边框梁柱节点为刚接.

所得到的基底剪力-侧移曲线如图11所示．分层立柱与贯通梁的连接刚度越强，框架整体抗侧刚度和抗侧承载力水平略微增大，表明分层立柱节点刚度也可提供一定结构刚度．但整体抗侧承载力变化幅度不大，结构整体失效模式不受影响，因此分层立柱节点对于结构性能影响有限．故考虑施工便捷性，可采用非加劲端板螺栓连接或采用限位铰接连接，且在结构设计中，分层立柱可偏安全假定为铰接．

图11 分层立柱连接刚度的影响

3.3 边框梁柱连接刚度

框架梁、柱在理论分析阶段假定为刚接节点，但实际连接中可采用加强型栓焊混合或全螺栓节点连接，如图12所示，前者可实现刚接性能，后者一般为半刚接．为揭示边框梁柱连接刚度影响，以指导框架节点选型和设计，可通过释放水平贯通梁端部约束刚度的方式分析框架节点刚度对结构抗侧性能影响．

分别模拟边框梁柱节点分别为刚接、75%刚度、50%刚度、25%刚度和铰接5种工况(图13(a)中工况a～e)．该分析中支撑均居中设置，分层立柱与贯通梁为铰接．

图13(a)为不同边框梁柱连接刚度工况下基底剪力-侧移曲线．当梁柱连接为刚接或刚度释放小于50%时，框架抗侧承载力曲线基本无变化，构件屈服失效顺序与图7中承载过程一致，符合预期屈服失效顺序．当边框梁柱刚度释放50%时，支撑屈服后框架抗侧刚度略微减小，承载力水平基本无变化，但此时边框柱脚先于梁端进入屈服，与图8中失效模式一致.

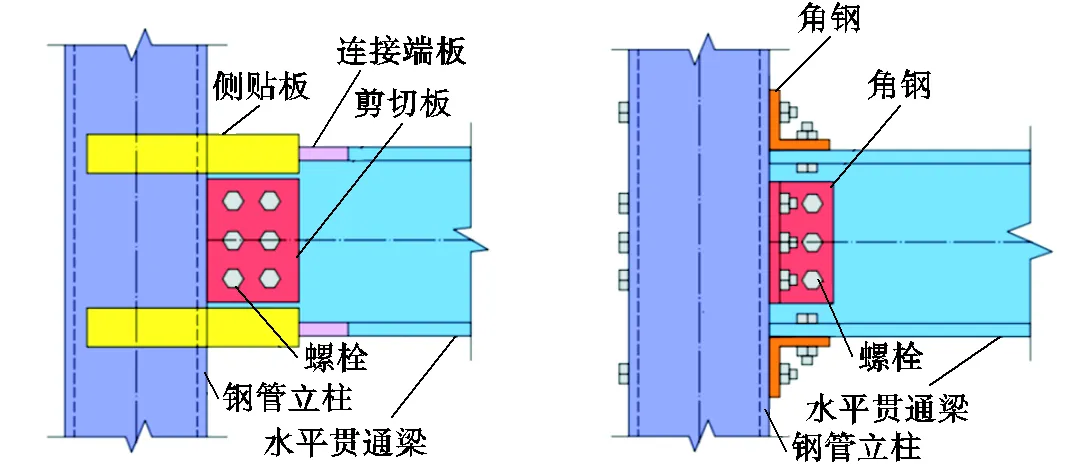
（a）刚性节点 （b）半刚性节点

图12 边框梁柱连接节点模式

Fig.12 Frame beam-column connection node

（a）基底剪力-侧移曲线

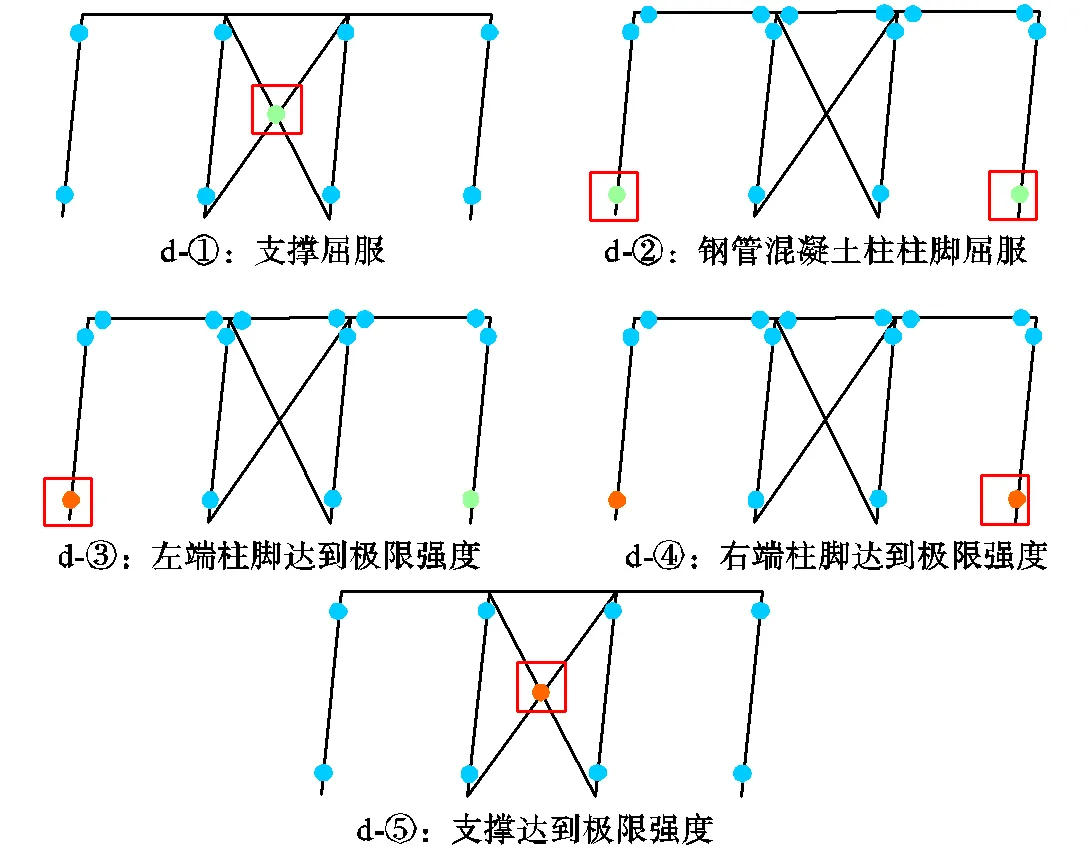
（b）边框梁柱25%刚度节点工况失效模式

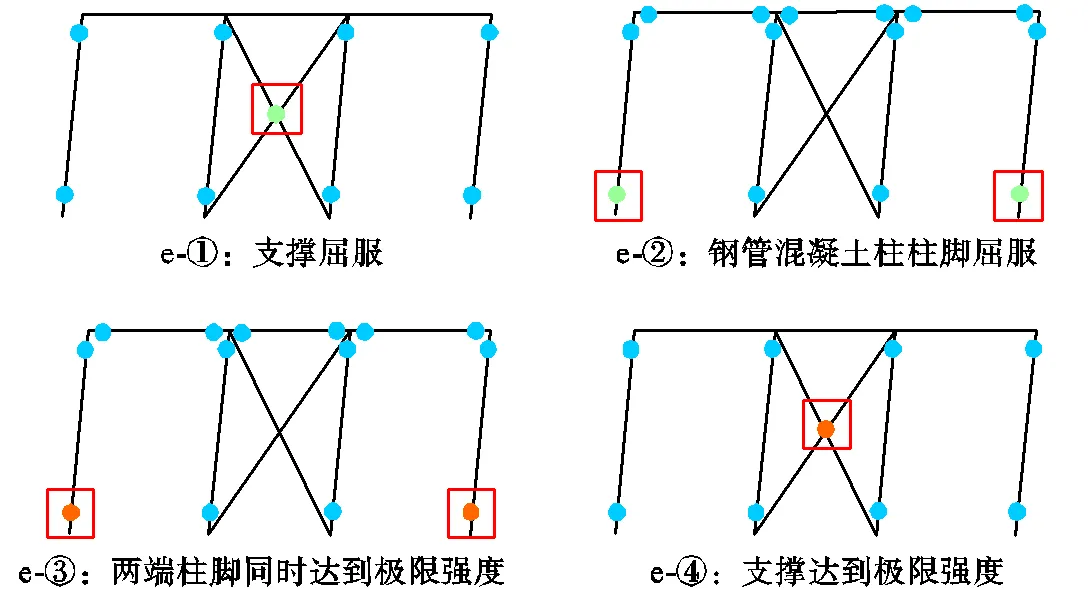
（c）边框梁柱铰接节点工况失效模式

图13 边框梁柱连接刚度影响

Fig.13 Influences of the beam-to-side column connection stiffness

当边框梁柱连接刚度释放高于50%，支撑屈服后框架抗侧刚度进一步降低．图13(b)所示为边框梁柱连接为25%刚度工况的失效模式．随着侧移的加大，受拉支撑首先发生屈服，抗侧刚度略微下降．之后钢管混凝土柱脚发生屈服，抗侧刚度进一步降低，仅为初始刚度的10.9%．当柱脚达到极限强度时，整个框架丧失承载能力．此工况下支撑屈服后主要边框柱提供主要抗侧性能，框架主要产生边框柱脚的屈服和失效，并进而影响整体框架的弹塑性承载性能．

图13(c)所示为边框梁柱采用铰接节点时失效模式．边框梁柱为铰接节点时整体框架初始抗侧刚度相较于其他工况偏低．支撑屈服后框架塑性刚度和抗侧承载力水平下降较为显著，此工况下支撑为主要的抗侧承载来源．边框柱脚屈服时结构抗侧刚度下降91.5%．最后边框柱脚同时达到极限强度，承载曲线发生突降．

对比结果可见，边框梁柱节点刚度对于框架抗侧时各部件承载机制和整体框架的抗侧刚度和承载力水平均有较为显著影响，边框梁柱刚度较小或为铰接时贯通梁基本不参与结构抗侧承载．因此边框梁柱连接刚度不宜过小，节点抗弯刚度宜控制在75%的梁截面刚度以上．因此可采用焊接、栓焊混合或加强型螺栓连接方式．

4 结 论

本文在现有分层装配柔性支撑框架基础上提出了改进的铰接支撑双重抗震改进型轻钢框架体系.采用理论分析方法得到改进型框架梁、柱、支撑等构件初步设计方法，并基于Pushover分析改进型框架弹塑性抗侧承载性能和关键结构参数影响规律，得到以下结论．

(1) 所提出的改进型框架具有多重抗侧承载机制，其中柔性支撑提供初始抗侧能力．当作为第1道抗震防线的柔性支撑屈服后，支撑外围框架作为第2道抗震防线提供后续抗侧和抗震储备．

(2) 改进型框架结构传力清晰，可基于结构力学方法预判结构承载和失效机制，有效得到结构设计准则以实现支撑-梁-柱的屈服顺序，实现该结构体系双重抗震防线稳定、延性好等优势．

(3) 改进型框架支撑和梁端屈服时不会引发结构承载力的突降，边框柱脚塑性和失效对结构承载力影响较为显著．柔性支撑与边柱之间的距离建议大于1m，可使得支撑位置变化基本不影响结构抗侧承载性能．内部分层立柱节点刚度对结构抗侧性能影响较小，其中铰接工况下抗侧刚度和承载力相较于刚接工况仅下降2.54%和6.35%，实际设计中可采用全螺栓连接或限位铰接．边框梁柱连接刚度将影响外围框架刚度和结构失效机制，其铰接工况下框架承载力和刚度相较于刚接工况分别下降18.68%和14.09%，实际设计中建议采用加劲型螺栓连接．

(4) 内部立柱和柔性支撑可藏于墙内，可基于屋内功能需求灵活变换位置．体系中各节点均可在保障结构性能条件下采用螺栓连接以实现全装配化建造．

［1］ 龚永智，柯福隆，谭涛，等. 全干法连接装配式夹芯剪力墙结构抗震性能研究[J]. 天津大学学报(自然科学与工程技术版)，2022，55(5)：451-461.

Gong Yongzhi，Ke Fulong，Tan Tao，et al. Seismic behavior of assembled sandwich shear wall structure connected by full dry method[J]. Journal of Tianjin University(Science and Technology)，2022，55(5)：451-461(in Chinese).

［2］ 乔文涛，杨洋，肖剑. 钢结构现浇楼板施工中快速拼装模板体系[J]. 天津大学学报(自然科学与工程技术版)，2016，49(增1)：80-87.

Qiao Wentao，Yang Yang，Xiao Jian. High-efficient assembling formwork system for cast-in-place floor construction in steel structures[J]. Journal of Tianjin University(Science and Technology)，2016，49(Suppl 1)：80-87(in Chinese).

［3］ 曹万林，杨兆源，周绪红，等. 装配式轻钢组合结构研究现状与发展[J]. 建筑钢结构进展，2021，23(12)：1-15.

Cao Wanlin，Yang Zhaoyuan，Zhou Xuhong，et al. Research and development on prefabricated lightweight steel composite structures[J]. Progress in Steel Building Structures，2021，23(12)：1-15(in Chinese).

［4］ 刘占科，靳璐君，周绪红，等. 钢构件整体稳定直接分析法研究现状及展望[J]. 建筑结构学报，2021，42(8)：1-12.

Liu Zhanke，Jin Lujun，Zhou Xuhong，et al. State-of-the-art on research of direct analysis method of steel members with global instability[J]. Journal of Building Structures，2021，42(8)：l-12(in Chinese).

［5］ 周绪红，邹昱瑄，徐磊，等. 冷弯薄壁型钢-钢板剪力墙抗震性能试验研究[J]. 建筑结构学报，2020，41(5)：65-75.

Zhou Xuhong，Zou Yuxuan，Xu Lei，et al. Seismic behavior of cold-formed thin-walled steel plate shear wall[J]. Journal of Building Structures，2020，41(5)：65-75(in Chinese).

［6］ 管宇，周绪红，石宇，等. 轻钢组合楼盖面内刚度和承载力计算方法研究[J]. 湖南大学学报(自然科学版)，2019，46(9)：31-43.

Guan Yu，Zhou Xuhong，Shi Yu，et al. Study on calculation method for in-plane stiffness and bearing capacity of thin-walled steel composite floor[J]. Journal of Hunan University(Natural Sciences)，2019，46(9)：31-43(in Chinese).

［7］ 石宇，曾乐，向弋，等. 新型冷弯薄壁型钢板剪力墙抗侧性能试验研究[J]. 建筑钢结构进展，2021，23(7)：21-30.

Shi Yu，Zeng Le，Xiang Yi，et al. Experimental study on the lateral performance of new cold-formed thin-walled steel plate shear walls[J]. Progress in Steel Building Structures，2021，23(7)：21-30(in Chinese).

［8］ 叶露，王宇航，石宇，等. 冷弯薄壁型钢框架-开缝钢板剪力墙力学性能研究[J]. 工程力学，2020，37(11)：156-166.

Ye Lu，Wang Yuhang，Shi Yu，et al. Study on the mechanical properties of cold-formed steel framed shear wall with slits[J]. Engineering Mechanics，2020，37(11)：156-l66(in Chinese).

［9］ 叶继红. 多层轻钢房屋建筑结构-轻钢龙骨式复合剪力墙结构体系研究进展[J]. 哈尔滨工业大学学报，2016，48(6)：l-9.

Ye Jihong. An introduction of midrise thin-walled steel structures：Research progress on cold-formed steel framed composite shear wall systems[J]. Journal of Harbin Institute of Technology，2016，48(6)：1-9(in Chinese).

［10］ Wang Xingxing，Ye Jihong. Cyclic testing of two- and three-story cold-formed steel(CFS)shear walls with reinforced end studs[J]. Journal of Constructional Steel Research，2016，121：13-28.

［11］ 刘 洋，陈志华，刘佳迪，等. 柱承重式钢结构模块建筑抗震性能试验研究[J]. 天津大学学报(自然科学与工程技术版)，2021，54(2)：122-132.

Liu Yang，Chen Zhihua，Liu Jiadi，et al. Experimental study on seismic performance of corner-supported modular steel buildings[J]. Journal of Tianjin University(Science and Technology)，2021，54(2)：122-132(in Chinese).

［12］ 曹万林，刘子斌，刘 岩，等. 装配式轻型钢管混凝土框架-复合墙共同工作性能试验研究[J]. 建筑结构学报，2019，40(8)：12-22.

Cao Wanlin，Liu Zibin，Liu Yan，et al. Experimental study on combining effect of assembled lightweight CFST frames with composite walls[J]. Journal of Building Structures，2019，40(8)：12-22(in Chinese).

［13］ 王 伟，陈以一，余亚超，等. 分层装配式支撑钢结构工业化建筑体系[J]. 建筑结构，2012，42(10)：48-52.

Wang Wei，Chen Yiyi，Yu Yachao，et al. Floor-by-floor assembled steel braced structures for prefabricated buildings[J]. Building Structure，2012，42(10)：48-52(in Chinese).

［14］ 刘大伟，王 伟，马场峰雄，等. 分层装配式钢结构体系新型支撑研制与性能试验[J]. 建筑结构，2012，42(10)：57-60，86.

Liu Dawei，Wang Wei，Baba Mineo，et al. Development and behavior testing of innovative braces of floor-by-floor assembled steel structures[J]. Building Structure，2012，42(10)：57-60，86(in Chinese).

［15］ Wang Wei，Zhou Qing，Chen Yiyi，et al. Experimental and numerical investigation on full-scale tension-only concentrically braced steel beam-through frames[J]. Journal of Constructional Steel Research，2013，80：369-385.

［16］ GB 50011—2010 建筑抗震设计规范[S]. 北京：中国建筑工业出版社，2010.

GB 50011—2010 Code for Seismic Design of Buildings[S]. Beijing：China Architecture & Building Press，2010(in Chinese).

［17］ 沈祖炎. 钢结构基本原理[M]. 3版. 北京：中国建筑工业出版社，2018.

Shen Zuyan. The Basic Principle of Steel Structure[M]. 3rd ed. China Architecture & Building Press，2018(in Chinese).

［18］ 中国工程建设标准化协会. CECS 159：2004 矩形钢管混凝土结构技术规程[S]. 北京：中国计划出版社，2004.

China Association for Engineering Construction Standardization. CECS 159：2004 Technical Specification for Structures with Concrete-Filled Rectangular Steel Tube Members[S]. Beijing：China Planning Press，2004(in Chinese).

Hinged-Brace Dual-Resistance Frame and the Elastic-Plastic Lateral Force Resistance Analysis

Yu Yujie1，Wei Quanfei1，Wang Xiaoxiang2, 3，Hu Wanying1

(1. School of Civil Engineering，Central South University，Changsha 410075，China；2. Hunan Construction Investment Co.，Ltd.，Changsha 410004，China；3.Hunan Construction Engineering Group Co.，Ltd.，Changsha 410004，China)

An enhanced hinged-brace dual-resistance light steel frame system was proposed based on the current design of layered assembly brace frame systems. Columns located at the corner of the wall or along the sidewall remain the vertically continuous construction. The interior structure adopts the through-beam layered-column design. Flexible cross braces are set between the internal layered columns to provide the initial lateral structural stiffness. The horizontal through beams are rigidly or semi-rigidly connected to the continuous side columns to form the peripheral frame，providing the subsequent lateral force resistance. This leads to the formation of the second lateral seismic defense. Theoretical analysis was performed to obtain the preliminary design method of beams，columns，and braces in the improved frame. The elastic-plastic lateral force resistance and influences of critical structural factors were analyzed based on Pushover simulations. The structure possesses a clear force transfer mechanism and multiple lateral load resistance mechanisms. The structural design criteria can be effectively obtained based on the structural mechanics method. Given a certain distance from the side column, the position changes of the hinged brace do not affect the lateral load resistance. The connection stiffness of internal layered columns has minimal influence on the structural lateral performance，allowing for the full bolted or hinge joints to be applied. The bending stiffness of the through-beam to the side column connection can impact the structural stiffness of the peripheral frame and further influence the failure mechanism of the entire structure. Stiffened bolted connections were proposed to ensure   sufficient connection stiffness in practical structural designs. All connections in the improved frame can employ bolted connections to achieve the full assembly construction while retaining satisfactory structural mechanical performance.

hinged-brace dual-resistance frame；assembly construction；lateral force resistance；mechanical analysis；Pushover analysis

10.11784/tdxbz202304025

TU311.41

A

0493-2137(2024)04-0343-12

2023-04-13；

2023-06-09.

余玉洁（1990—  ），女，博士，教授.

余玉洁，yujiecsu@csu.edu.cn.

国家自然科学基金资助项目(52278231)；湖南省自然科学基金资助项目(2022JJ20073)；湖南省科技创新计划资助项目(2022RC1185)；长沙市自然科学基金资助项目(kq2202100).

the National Natural Science Foundation of China(No. 52278231)，the Natural Science Foundation of Hunan Province，China(No. 2022JJ20073)，the Science and Technology Innovation Program of Hunan Province，China(No. 2022RC1185)，the Natural Science Foundation of Changsha City，China(No. kq2202100).

(责任编辑：金顺爱)