基于结构优化的聚风装置流场特性数值研究

徐恺，黄成，黄家庚

（河南科技大学机电工程学院，河南 洛阳 471003）

0 引言

我国风能资源丰富，但目前采用的叶片式风电机对低风速不敏感，有效工作风速在5.2 m/s以上[1]。文献[2]提出了一种管道式风力发电系统，命名为INVELOX，该类管道式风能采集装置不需要安装涡轮机塔。

为了提高INVELOX系统工作效能，减小损失，研究人员尝试了多种减小溢出的方法。为了提高INVELOX的气动性能，文献[3]设计了新型窗帘式结构，并对两种帘式结构和它们的组合结构进行了数值模拟，结果表明，采用延长导流板的帘式结构对INVELOX系统中流速比（SR）有明显提高。文献[4]研究了结构几何参数对INVELOX气动性能的影响，结果表明，当进气口投影面积和文丘里管横截面积之比为33.6时达到最佳比，此时采用6.7 m/s作为流场风速时，SR值最大，约为1.7。文献[5，6]通过安装单台、双台和三台风电机组对电学输出进行性能测试，得出相同条件下每个风力涡轮机的输出电压和功率，证明了涡轮机数量对总功率的非线性影响；与传统风力机相比，由于无需额外基础设施，安装多台机组对使用成本没有显著提高。为解决INVELOX出口气流受自然风的阻碍，文献[7]采用CFD方法对INVELOX风力发电系统进、出口结构进行优化分析，通过改变出口气流方向减小出口气流受自然风的阻碍。上述研究对INVELOX系统有很大改进，增强了对风的俘获效率，但要实现真正意义的全方向风能俘获，不仅要对不同夹角的水平来流风向进行流场分析，还需要对系统的工作风速进行测定，以及对来流风向与水平面成一定倾斜角时流场、不同工况下流场特性及SR值进行分析。

本文设计了一种小型风能采集装置，采集装置结构上采用了文献[3]的帘式结构，采用计算流体软件XFlow对采集装置进行气动性仿真模拟。由于无网格的格子玻尔兹曼方法可以在很大程度上节约前处理时间，并避免因网格质量问题带来的计算误差，因此，本文采用无网格的格子玻尔兹曼方法对不同水平风向和倾斜风向下的文丘里管中的平均风速进行计算，分析不同夹角下的SR值，确定其满足工作要求的风向角度。最低工作风速是此类装置在现实环境中得到应用的关键因素，风速为2～5 m/s的地区约占我国风能资源的85%，INVELOX系统对风速要求较低，可广泛应用于低风速区域的风能采集。

1 风采集装置模型

1.1 结构模型

本文设计的采集装置模型在三维制图软件UG12.0中以弯管上端圆中心点为坐标原点进行建模，为方便在XFlow中对模型进行几何变换，将该采集装置（图1）分为上、下两个部分，上部分由聚风锥管、凸台和导流板组成，下部分由文丘里管和一段90°弯管组成，将模型保存为.STP格式的三维实体导入XFlow中进行流场分析。

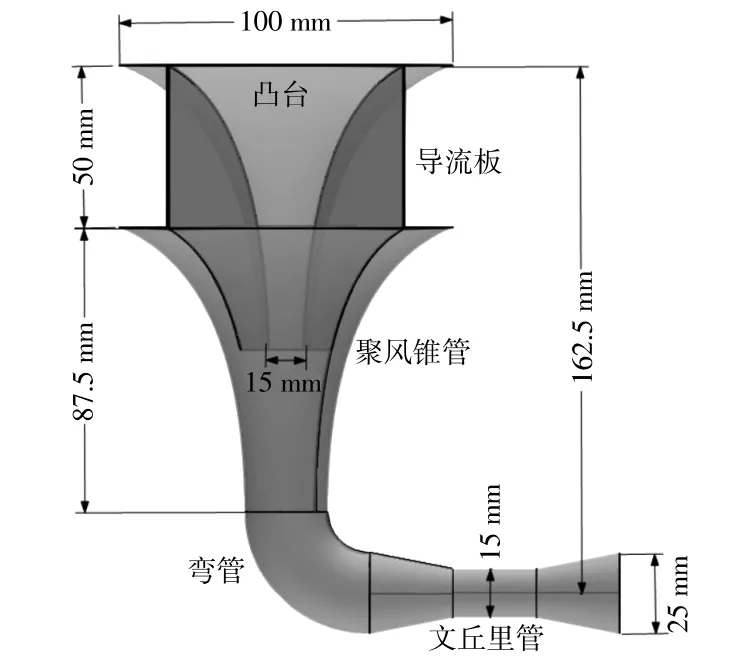
图1 模型示意图Fig.1 The sckematic drawing of samples

图1中，进气口高度为50 mm，上端长为100 mm，文丘里管工作段外径为15 mm、内径为14 mm，整个装置所有薄壁厚度均为0.5 mm。该采集装置进风口面积与文丘里管工作段截面积之比为32.48，与文献[3]中的最佳比值33.6十分接近，有利于对环境中风的采集。

1.2 数值模型

传统CFD通过有限元和有限体积法求解纳维-斯托克斯方程得到流场信息。本文采用的XFlow软件是基于格子玻尔兹曼方程模型，描述的流体粒子具有一定的离散速度，其分布函数为在固定的方格上的运动过程。该方程通常由流体粒子基于分布函数的演化方程、格子结构及离散速度集合3部分构成。在具有离散速度的连续空间介质中，格子玻尔兹曼方程[8]为

式中：fi为粒子密度分布函数；ei为沿格子方向的速度；Ωi为碰撞作用算子；n为该LBM模型的不同格子速度总数。

Xflow软件采用D3Q27模型进行计算，其中3表示维度，27表示该模型有27个速度向量。

2 仿真验证

2.1 网格无关性验证

为避免分辨率设置使网格数量不同带来的计算误差，本文采用0.04，0.05 m和0.06 m 3种不同的远场分辨率，加密方法采用近壁面自适应格子加密及尾流加密，近壁面分辨率为远场分辨率的1/16倍。在来流风速为6 m/s的风场，3组不同分辨率的文丘里管中的平均速度如表1所示。

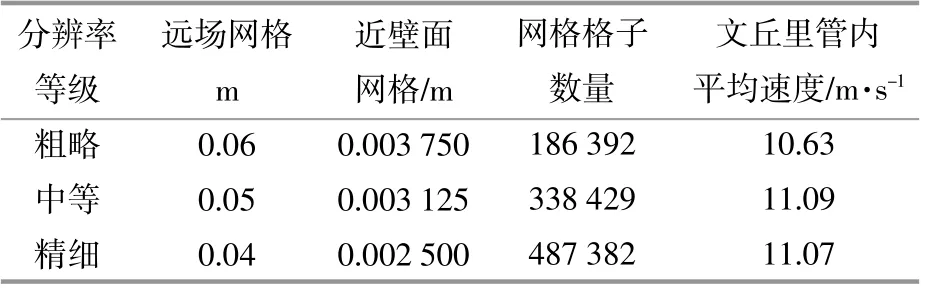
表1 3组分辨率参数Table 1 Three sets of resolution parameters

由表1可知，3组网格下文丘里管内速度变化差别不大，特别是中等和精细分辨率等级下的平均速度基本相同。在保证精度条件下，为节约计算成本，采用中等分辨率等级作为后续计算依据。其中远场分辨率为0.05 m的文丘里管内的速度随时间变化曲线如图2所示。

图2 分辨率为0.05 m时速度随时间变化曲线Fig.2 Speed vs.time when the resolution is 0.05 m

2.2 对比验证

为进一步证实仿真可靠性，本文采用的物理模型和入口流速与文献[3]基本保持一致，并进行对比仿真验证。设置入口流速为6.7 m/s，创建Custom field自定义函数，并设置Custom field函数为流速比，即：

本文采用优化结构，由式（2）得到的SR约为1.78，计算结果相较于文献[3]有小幅提高。通过对比发现，在凸台最下方进风口处以及下方聚风锥管周围的风速分布略有差异，上方凸台母线曲率的不同可能是造成文丘里管内SR值较大的原因之一。文献[9，10]对造成的原因做了分析和说明，比如扩散器截面几何变化、聚风锥管线型函数不确定性等。采集器工作段部分的速度云图和文丘里管扩散器周围流场特性与文献[3]基本一致。图3为本文计算结果和文献[3]对称面内SR云图。

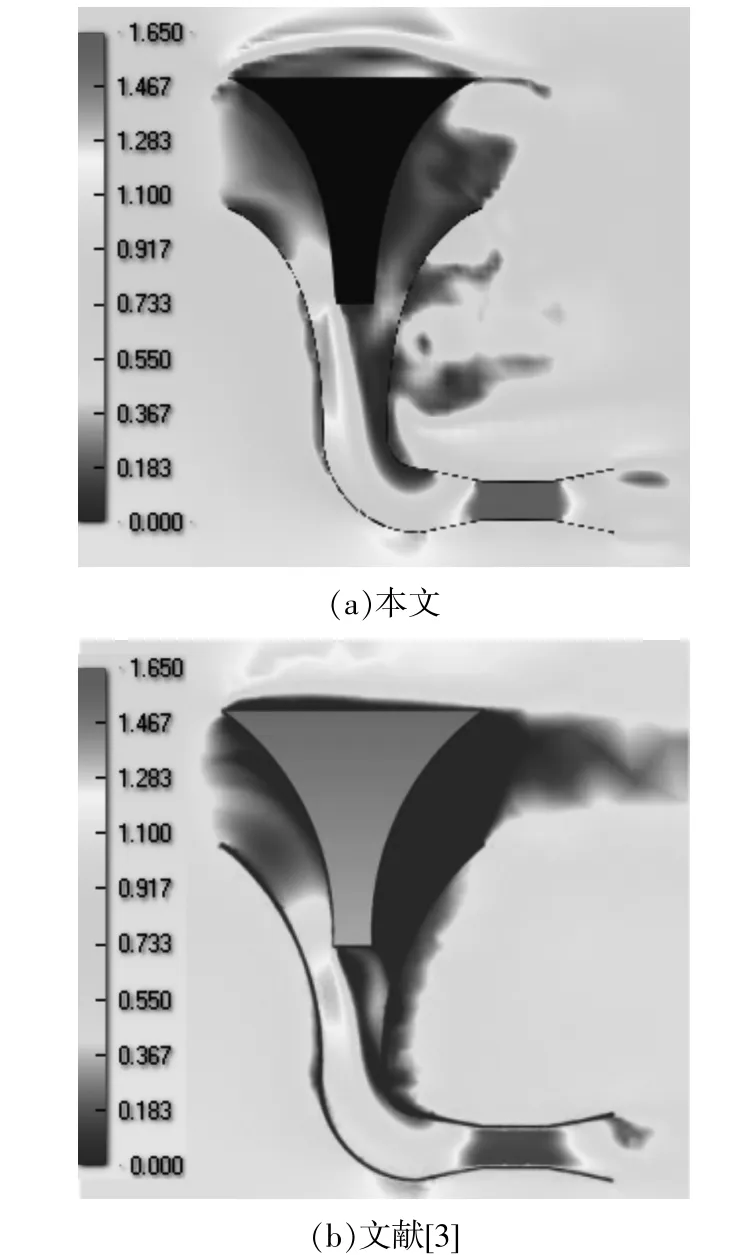
图3 对称面内SR云图Fig.3 Contrast cloud map for plane of symmetry

2.3 仿真条件设置

基于格子玻尔兹曼方法的XFlow软件为用户提供的虚拟风洞可直接将.STP型导入，不需要划分网格，预处理器可以根据输入几何和每个几何的分辨率生成原始的八叉树晶格结构，当涡度达到阈值时，网格会自动细化。因此，需要定义3种分辨率：远场分辨率、尾迹分辨率和近壁分辨率[11]。本文选用3d流场，在文丘里管中心轴线位置建立插值点监控速度，仿真时间为5 s，设置湍流强度为5%，计算域边界条件如表2所示。

表2 计算域边界条件设置Table 2 Boundary setting of the computational domain

针对XFlow软件提供的Automatic模型、Smagorinsky模型、Dynamic Smagorinsky（DSM）模型、壁面自适应局部涡粘性模型（WALE）等不同湍流模型，以6 m/s作为流场风速，计算不同模型下文丘里管内平均速度以及SR比值（表3）。

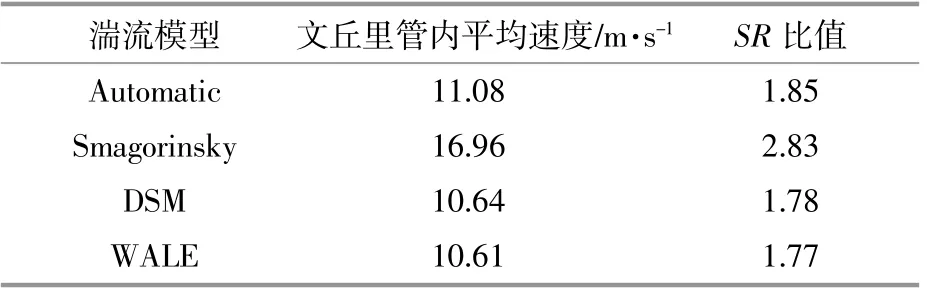
表3 不同湍流模型下文丘里管内平均速度以及SR比值Table 3 The average velocity and SR ratio in the lower turbulence model of different turbulence models

由表3可知，采用Automatic模型作为基准时，除Smagorinsky模型外，其它湍流模型的误差均不超过5%。依据软件用户手册及文献[12]中类似工程模拟，造成Smagorinsky模型误差较大的原因是，该模型与DSM模型具有较高的涡粘性和各向同性假设，不能准确预测壁面附近流体流动。WALE模型在靠近和远离壁面以及层流和湍流的情况下均具有良好的特性，因此，在之后的计算中均采用WALE模型进行流场分析。

3 计算结果及分析

3.1 不同风速下SR值及工作风速

为测定该风能采集装置的工作效率，选取流场风速为1.8～6.6 m/s，将此范围分为16个流场风速，每个流场风速间隔为0.3 m/s。在不同来流风速下对其进行流场特性仿真分析，通过监测文丘里管内平均风速变化，得到不同风速场下SR值。对不同流场风速下的SR值进行曲线拟合，并求出拟合曲线的斜率曲线，该斜率可以表征采集装置对流场风速增强速率的快慢。不同流场风速下的SR值、SR值拟合曲线以及拟合曲线的斜率曲线如图4所示。

图4 不同流场风速下V-SR及SR斜率曲线Fig.4 V-SR value and slope curve under different flow field and wind speed

由图4可知：当流场风速为3 m/s时，SR值在1.03左右，证明此风速下该风能采集装置对流场风速开始有增强作用；随着流场风速的增加，文丘里管内SR值随流场风速的提高而随之增大，证明系统对流场风速的增强效果愈加明显；由斜率曲线可知，当流场风速为2.1～4.2 m/s时，SR增速较大，表明在低风速下该装置增强风速的效果更好，当流场风速达到5.1 m/s后，SR的增长速率逐渐放缓，保持在0.2以内。

3.2 不同水平风向角

为探究风向的影响，首先考虑水平方向的来流风。由于在水平方向上，该装置为左右对称结构，因此计算了水平面内流场方向与文丘里管中心轴线夹角α为0～180°时SR值的变化情况。将该平面内流场分为13个方向，水平夹角风向示意图如图5所示。

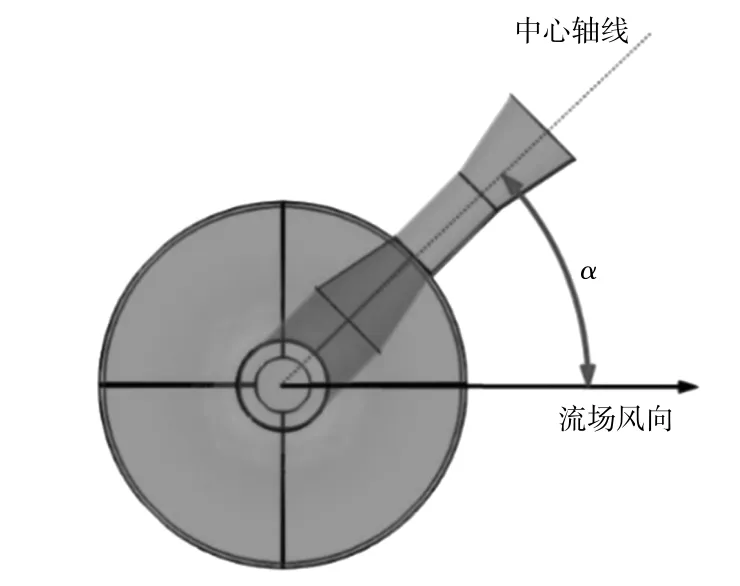
图5 水平夹角示意图Fig.5 Schematic diagram of horizontal angle

将0～180°风向下的SR值做一个对称，即可得到-180～180°（顺时针取正）方向上不同水平风向角下的SR值（图6）。

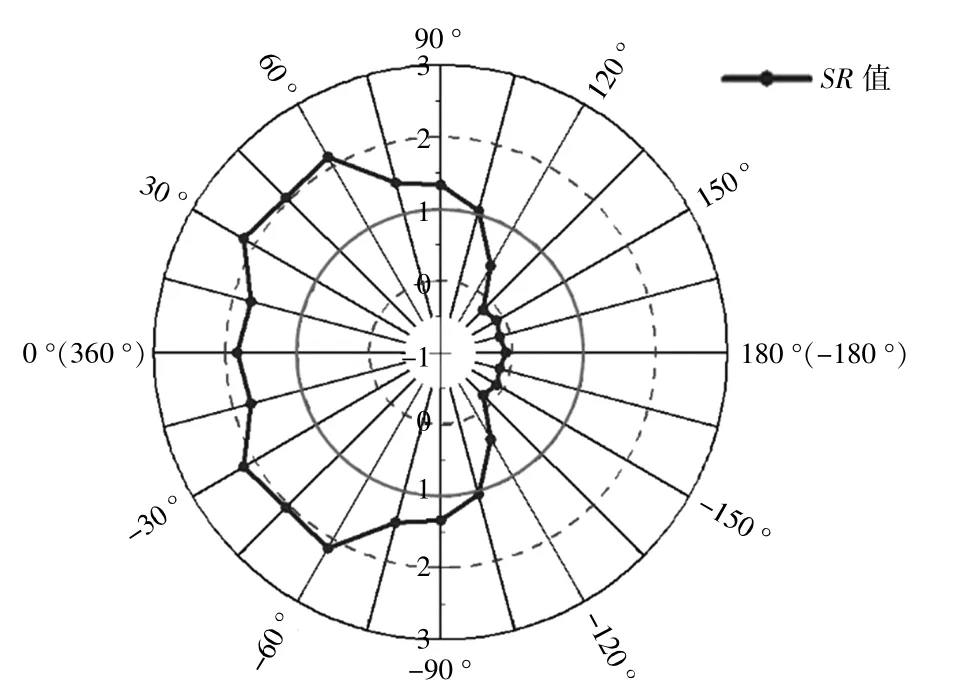
图6 不同水平风向角下SR值Fig.6 SR values at different horizontal wind direction angles

由图6可知：当水平风向夹角为-60～60°时，SR值均在1.5以上，证明该装置对流场中风速增强作用较强；当夹角继续变大，这种增强作用开始降低，特别是当夹角达到105°以后，SR值小于1，无法实现对环境中来流风加速的效果，造成该情况的主要原因是文丘里管扩散段内产生了风倒灌，这是此类风电系统在广泛应用中亟需解决的主要问题之一。

3.3 不同倾斜风向角

结合现实环境中风可能存在的来流方向，计算了来流风向与风能采集装置的水平面倾斜角β取值为0～360°时不同风向的SR值（图7）。将360 °均匀分为24个方向，即每个方向夹角为15°，流场风速设置为6 m/s，不同倾斜角下的SR值如图8所示。

图7 倾斜角示意图Fig.7 Schematic diagram of tilt angle

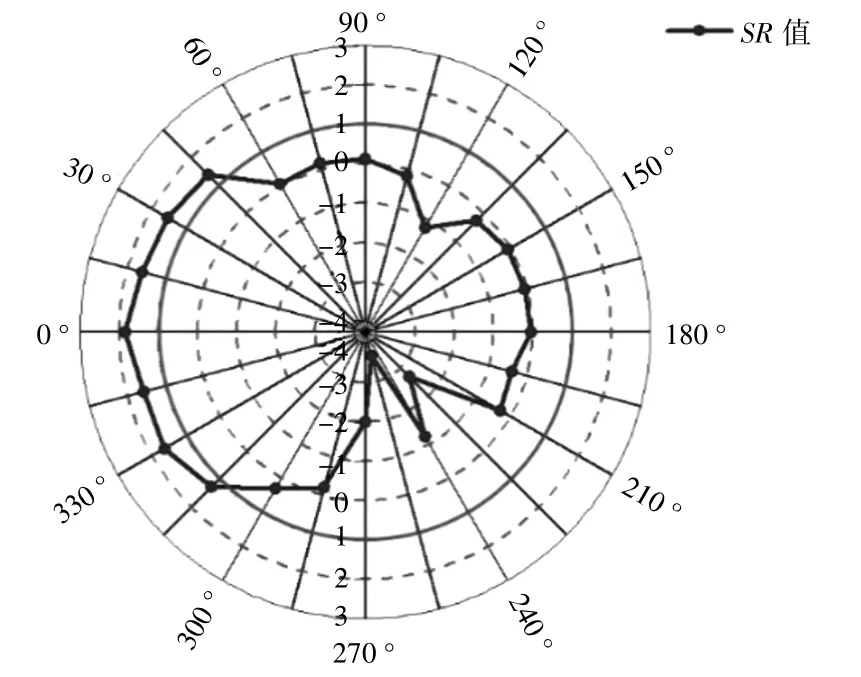
图8 不同倾斜角下SR值Fig.8 SR value under different tilt angles

由图8可知：当倾斜角为0 °时，该采集装置增速效果最好；当倾斜角为0～45 °和315～360 °时，该装置对风速有增强作用；当来流风向在其它倾斜角度下，SR值小于1，在第三象限内的角度下，SR值为负值。倾斜风向下，文丘里管内速度有一定幅度的波动，特别是在第三象限角度下，其原因是复杂的，主要是受流场风向及流场压强影响。

针对影响风速变化的主要因素，图9，10分别给出了倾斜风向角为30°和225°时瞬时速度矢量图及瞬时压力场云图。

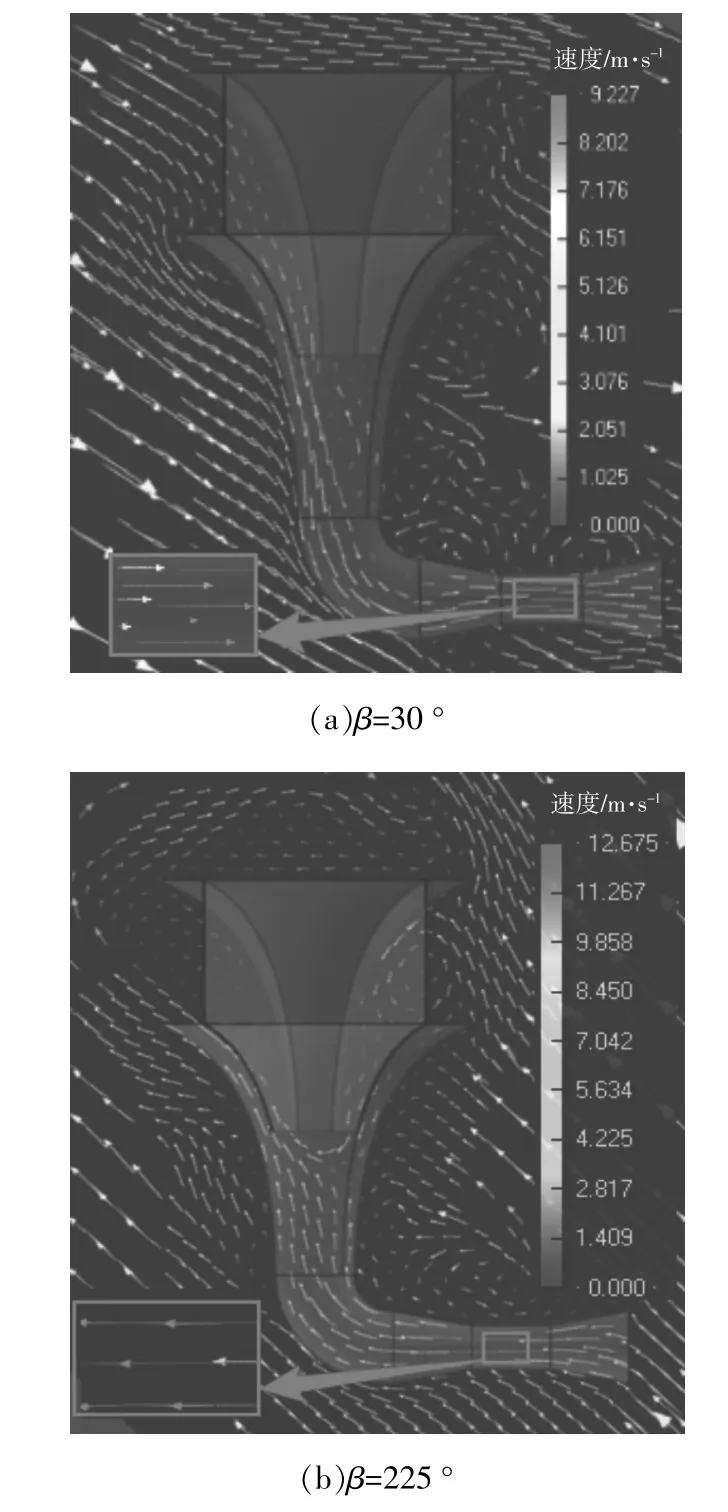
图9 瞬时速度对比矢量图Fig.9 Instantaneous speed comparison vector diagram

通过对流场特性的对比分析可知，影响文丘里管内SR值变化的原因主要有以下几点。

①入口风向投影面积的影响。当倾斜角为0～45°时，文丘里管内风速会随着入口风向投影面积的减小而减小[图9（a）]，此时风的流向有利于将风送入文丘里管内，因此在该角度区间内风能采集装置对流场风速有较高的提升。

②流场风向的影响。当倾斜角为90～270°时，随着倾斜角不断变大[图9（b）]，流场内风的流向与该装置原理上出口风向相反，流场内风的流向不利于风从入口处流进文丘里管内，文丘里管内速度小于流场风速，当倾斜角超过105°后风倒灌，文丘里管内SR值为负值。

③进、出口附近压强的影响。通过对图10瞬时压力场分析可知，不同角度下来流风使装置进、出口附近产生不同的压强，当倾斜角为180～270°时，由于背风面附近风的流速快，导致入口处压强小，迎风面出口侧形成高压区，在压力差作用下，风从出口处流入，此时文丘里管内风向为反方向，且风速较高。

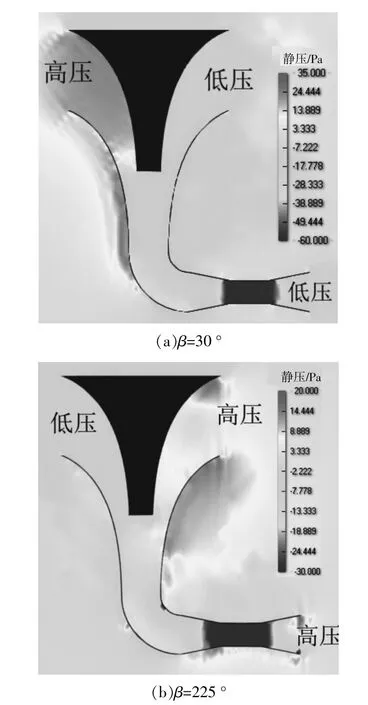
图10 瞬时压力对比云图Fig.10 Contrast cloud map of instantaneous pressure

风向的改变对文丘里管工作段风速影响较大，实际使用过程中应结合环境中的风向，在达到工作风速条件下，对该装置进行合理的安装，以达到装置最大工作效率。

4 结论

本文采用基于格子玻尔兹曼方法的流体力学软件XFlow对优化设计的风能采集装置进行流场特性研究，计算不同风速下文丘里管内风速的变化，并对该装置在不同水平风向夹角和倾斜风向夹角下文丘里管内平均速度变化进行计算，得到以下结论。

①通过案例对比，证实了采用基于格子玻尔兹曼方法的流体力学软件XFlow对所设计的风能采集装置进行流场分析的可行性。

②计算了风能采集装置在不同流场风速下对应的SR值，反映出不同风速下其对风速的增强能力的变化，0°水平风向下最低工作风速为3 m/s，且增强能力随着流场风速的增加而增加。

③在风速为6 m/s环境中，计算了风能采集装置在不同水平和倾斜风向夹角下的SR值。分析了不同夹角对文丘里管内风速增强效果的影响，给出了增强作用时（SR＞1）水平风向夹角α以及倾斜风向夹角β的取值范围。