考虑分布式可再生能源不确定性的配电网可靠性评估

刘海信，卢建刚，潘凯岩，3，赵瑞锋，黎皓彬，刘华，杨蒙萌

（1.东方电子股份有限公司，山东 烟台 264010；2.广东电网有限责任公司电力调度控制中心，广东 广州510000；3.哈尔滨工程大学智能科学与工程学院，黑龙江 哈尔滨 150000）

0 引言

近年来，随着光伏和风能在配电网中渗透率的不断提高，电力系统正处于从传统配电系统向智能电网转变的重要阶段[1-3]。虽然可再生能源在智能电网运行中具有诸多优点，但其不确定性和间歇性会造成电压波动、潮流计算复杂等问题[4]。由于配电网呈辐射状拓扑结构，配电系统在用户负荷点造成的停电比例较大。因此，对含有分布式发电（Distributed Generation，DG）机组和储能设备的配电系统进行可靠性评估至关重要。

配电系统的可靠性是衡量供电质量和能力的一个重要指标，影响配电系统可靠性的主要因素包括线路故障、配电系统组件故障、由自然因素造成的电力系统中断以及系统需求。为了保持系统良好的可靠性，对配电系统进行重新设计或配置，以解决由于过载、低电压调节、风力、山体滑坡等物理因素造成的系统频繁跳闸等问题。发电和输电复合系统可靠性评估方法主要包括3个方面：系统状态选择、状态计算和可靠性指数更新[5]。文献[6]探讨了电力储能系统的特性，以优化电力系统损耗、效率、可靠性和能源成本。文献[7]提出了一种融合经济学的方法，以估算光伏、风能和微型水电机组对环境可持续性的影响。文献[8]提出了一种遗传算法，用于优化由光伏-风能-柴油-电池混合能源系统组成的电力系统的倾销能量、生命周期成本和二氧化碳排放量。文献[9]提出了一种在独立系统中优化可再生能源组合的新方法，最大限度地降低系统的总成本。

为了确定主动分布式网络的最优拓扑结构，文献[10]提出了一种自适应鲁棒分布式扩展模型。文献[11，12]考虑了与负荷、电价、投资成本和运营成本有关的不确定性来源，却在优化过程中忽略了主动配电网的可靠性。文献[13]提出了一种网络重新配置方法，以提高传统配电系统的可靠性指数。文献[14]提出了一种伪动态规划方法，用于估算可靠性评估对配电系统的影响。在54总线配电网络上的测试结果表明了该方法在传统配电网络上的有效性。蒙特卡洛模拟（Monte Carlo Simulation，MCS）是一种用于计算含DG和储能单元的常规配电系统可靠性指数的有效方法[15-17]。虽然MCS技术可以有效地给出电力系统问题的近似解，但由于计算时间较长，在求解多目标大型电力网络问题时不易实现。

为实现可再生能源DG安装位置和容量配置的优化及可靠性评估，本文引入了一种多状态模型，用于描述风电机组和光伏机组不同组件在各自状态下的随机特性，并探讨了风电机组和光伏机组集成后如何提高常规配电系统的可靠性。与分析法和MCS法相比，本文提出的马尔科夫链蒙特卡洛（Markov Chain Monte Carlo，MCMC）方法可获得更多有关负荷点和系统可靠性指数的信息，减少并网模式下用户负荷点的电力中断频率和持续时间。

1 基于概率分布的DG多状态模型

由于自然资源本身的间歇性和随机性，DG的输出具有不确定性。为了获得主动配电网的可靠性，本文建立了DG的多状态模型，该模型同时考虑了主动配电网中DG的功率和工作状态。

1.1 光伏模型的非确定性

描述太阳辐照度规律的最佳分布是贝塔概率密度函数，因此太阳辐照度随机模型可建模为

式中：Γ为伽马函数；r和rmax分别为t时刻的太阳辐照度分布和光照强度最大值；ξa和ξb为伽马函数中由历史光照数据拟合的参数。

式中：rave和σ2分别为t时刻光照强度的均值和方差。

光伏输出与光照强度之间的关系可以用分段函数近似地表示为

式中：PPV为光伏输出；PSR为光伏阵列的额定功率；rC为光照强度常数。

根据式（1）～（4），光伏输出的概率密度函数可写成以下形式：

光伏输出的概率可以表示为

式中：PipS和PipX分别为第i个状态下光伏功率上限和下限。

1.2 风电模型的非确定性

风力发电机输出主要取决于风速，采用双参数威布尔分布描述风速的分布，其概率密度函数为

式中：v为风速；ξk为威布尔分布的状态参数；ξc为反映平均风速的比例参数。

风力发电机输出功率与风速之间的关系可近似表示为

式中：Pw，Prw分别为风力发电机的实际输出功率、额定功率；vi，vr和vo分别为切入风速、额定风速和切出风速。

k1和k2的计算式为

根据式（7）～（9），风力发电机输出的概率密度函数可写成以下形式：

风力发电机的输出概率可以表示为

式中：PiwS和PiwX分别为第i个状态下风力发电机功率上限和下限。

2 基于MCMC模拟的状态评估和可靠性指标

2.1 MCMC模拟建模法

假设每个组件都有两种状态，即上行和下行，如图1所示。

图1 风能和光伏系统的状态转换Fig.1 State transition diagram of wind and PV system

图中，αwtg和βwtg，αptg和βptg分别为风力发电机和光伏发电机的故障率和修复率。状态转换矩阵M可以表示如下：

其中M的非对角元素mij等于从状态i到状态j的转换率。对角元素mii的计算式为

式中：Ω为状态空间。

风能和光伏系统的平均故障时间（Mean Time To Failure，MTTF）可通过下式得出：

式中：I为单位阵。

系统处于上行和下行状态的概率可表示为

串联组件处于上行状态的概率用Ms-UP表示，概率为风电机组和光伏机组处于上行状态的概率乘积：

等效的修复率βs的计算式为

基于MCMC模拟的评估过程如下：

步骤1：初始化所有组件状态；

步骤2：确定模拟年数，并将初始时间设为0；

步骤3：为系统中的组件生成一个介于0～1的随机数。根据随机数确定组件的工作时间和恢复运行时间；

步骤4：根据式（12），计算状态转换矩阵M；

步骤5：根据式（14），计算网络中具有最小MTTF的组件；

步骤6：根据式（17），计算上行状态概率Ms-UP；

步骤7：为失效的组件生成一个新的随机数，计算状态转换矩阵M、上行状态概率Ms-UP及MTTF；

步骤8：记录负载点的正常运行时间和故障时间；

步骤9：根据式（18）和式（19），计算每年每个组件的故障数量和持续时间；

步骤10：确定是否模拟了设定时间。如果是，则跳至步骤11；否则，跳至步骤2；

步骤11：计算可靠性指标。

2.2 可靠性指标

配电系统的可靠性主要通过可靠性指标来评估，可靠性指标通常包括负荷点指标和系统指标。负荷点指标主要用于评估系统中单个负荷点的可靠性程度，而在负荷点指标基础上计算得出的系统指标则用于评估整个配电系统的可靠性。组件i的平均故障率αi是指在统计时间内组件的预期停电次数。系统指标主要有系统平均停电次数（System Average Interruption Frequency Index，SAIFI）、系统平均停电持续时间（System Average Interruption Duration Index，SAIDI）和电量不足期望值（Expected Energy Not Supplied，EENS）。其中：SAIFI表示一个系统在1 a中持续停电的总次数；SAIDI表示一个普通客户在1 a中所经历的停电时间；EENS表示全年系统电能不足期望值。

式中：Ni，Ui，Ci分别为组件i的停电客户数量、年平均停电时间、切负荷量；pi为对应的概率。

2.3 可靠性模型的优化

本文采用随机模糊期望值算子模拟有功功率损耗和电压稳定性的不确定性。目标函数为有功功率损耗的随机模糊期望值和电网电压极限的最大可能性，其中有功功率损耗的优化问题可以描述如下：

式中：E[Ploss]为有功功率损耗的随机模糊期望值。

式中：Cr{·}为可信度。

电网电压稳定性的优化问题为

式中：N为正态分布函数；kir为二进制变量，表示分支的拓扑状态；分别为母线j上接受的最小、最大电压；μVj和δVj为Vj的期望值和标准偏差；Mtree为径向网的分支数；Nbus为网络中的节点数。

3 案例分析

为验证所提方法的可行性和准确性，本文将在含有风能和太阳能的IEEE-33节点配电网上进行测试分析。测试系统的分支和负载数据来自文献[18]，该系统运行电压为12.66 kV，由33条母线、32个分支和5条联络线组成，有功功率和无功功率负载分别为3.715 MW和2.3 MVar，其网络拓扑结构如图2所示。实验在配备Inter Core i5-5257 2.7 GHz CPU，8 GB内存和macOS High Sierra操作系统的计算机上运行，采用Matlab R2022b实现所提出的评估策略。通过在测试系统上放置不同数量和位置的DG来分析所提出方法的性能。

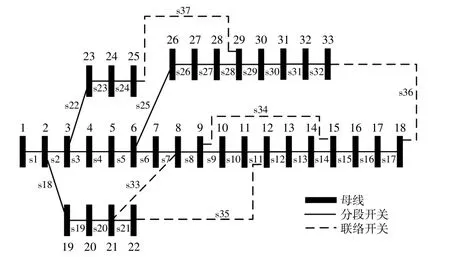
图2 IEEE-33节点测试系统单线结构Fig.2 One-line structure of IEEE-33 node test system

3.1 不同DG安装位置和容量的影响

在测试系统上分别安装1个和2个DG的情况下，对所提出的MCMC法与改进的粒子群优化算法（MPSO）[19]、遗传算法（GA）[18]及损耗灵敏度因子法（LSF）[18]进行比较分析，配电网有功功率损耗和电压曲线的结果如表1所示。

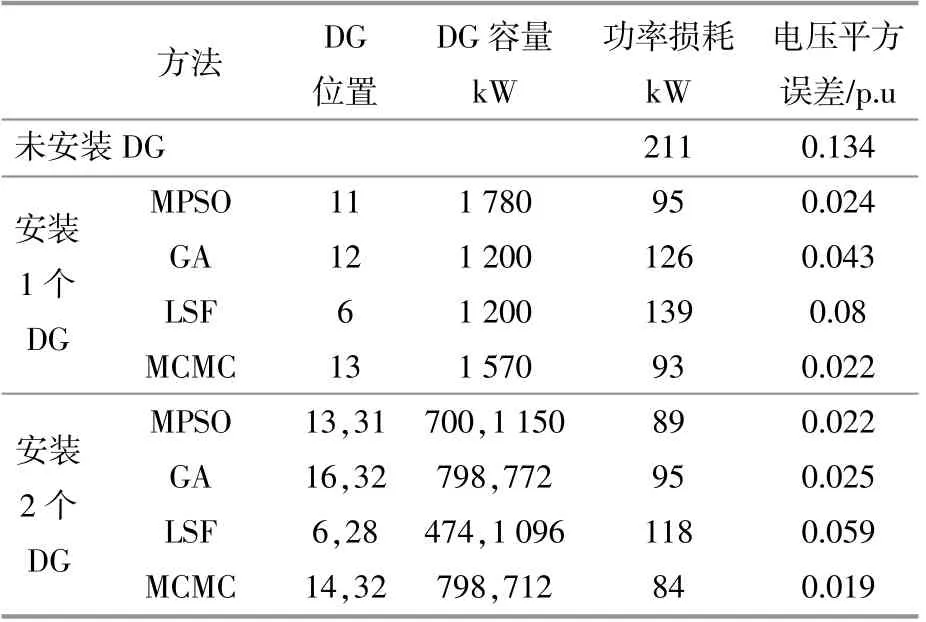
表1 在配电网中不同方法计算出的DG安装位置和容量对有功功率损耗和电压曲线的影响Table 1 Effect of DG installation location and capacity on active power losses and voltage profile calculated by different methods in distribution networks

对于安装1个DG的情况，MPSO法建议在11号母线上安装一台功率为1 780 kW的DG，这样配电网的有功功率损耗将减少至95 kW，电压平方误差降低至0.024 p.u；GA法建议在12号母线上放置一台1 200 kW的DG，可以将有功功率损耗减少至126 kW，电压平方误差降低至0.043 p.u；通过本文所提出的方法得到的结果是，在13号母线上安装一台功率为1 570 kW的DG，可以将有功功率损耗减少至93 kW，电压平方误差降低至0.022 p.u。对于安装2个DG的情况，MCMC法建议在14号母线和32号母线上分别增加798 kW和712 kW 2个DG单元，可以得到最优的DG位置和容量，这种配置可以将有功功率损耗减少至84 kW，电压平方误差降低至0.019 p.u。

在安装DG的情况下，测试系统有功功率损耗减少的百分比如图3所示。从图3中可以看出：对于安装1个DG的情况，MCMC法能够降低55.92%的有功功率损耗，MPSO法、GA法和LSF法分别能够降低54.97%，40.31%和34.21%的有功功率损耗；对于安装2个DG的情况，MCMC法相比其他3种方法具有最高的损耗下降率，这说明MCMC法能有效地降低网络损耗。

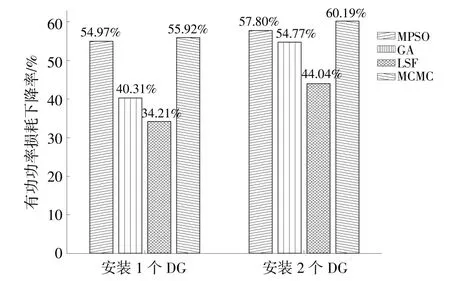
图3 有功功率损耗下降率Fig.3 Real power loss reduction

对于电压平方误差下降率的分析结果见图4。

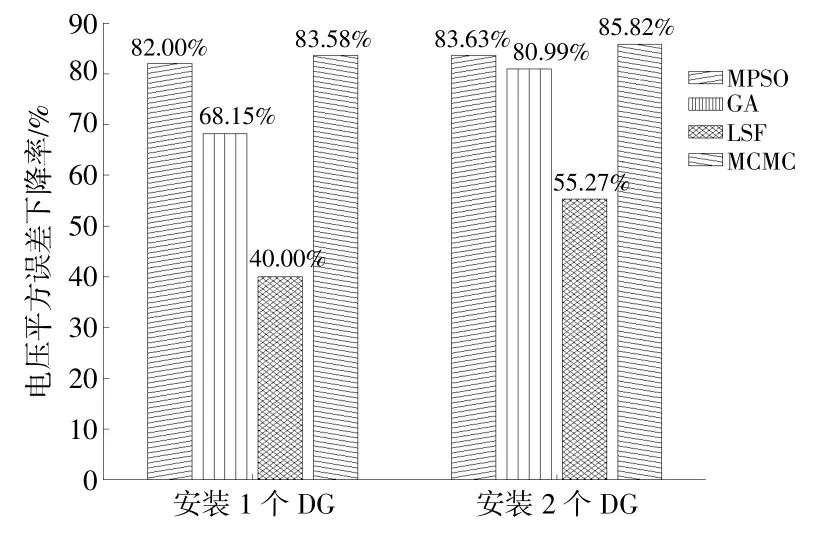
图4 电压平方误差下降率Fig.4 Voltage profiles square error reduction

从图4中可以看出，对于安装1个和2个DG的情况，MCMC法均具有较高的电压平方误差下降率。

MCMC法对各节点的电压提升如图5所示。结合表1中DG位置与图5中各节点电压可以看出，相比于未安装DG的配电系统，经MCMC法优化后的配置策略可以有效提升13～17号节点电压，基本修复了配电系统的欠压状态。通过在32号母线配置1个DG，有效地改善了测试系统远端的母线电压，这说明MCMC法对于改善电压具有积极的作用。

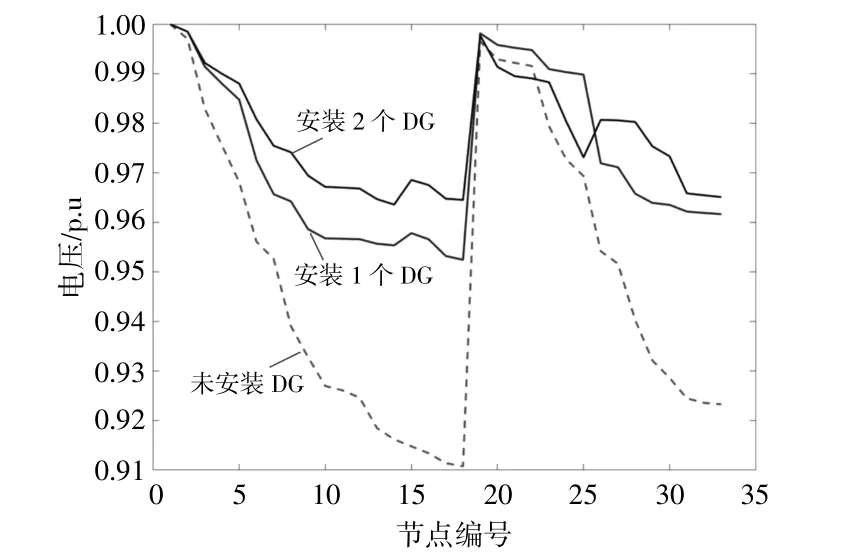
图5 在安装DG情况下MCMC法对测试系统各节点电压的影响Fig.5 Effect of the MCMC method on the voltage at each node of the test system with DG installed

3.2 可靠性评价

用于确定含DG配电系统的可靠性指数依赖于DG的两个可靠性数据：系统元件平均故障率（）和修复时间（βi）。本文考虑了不同情况下的DG可靠性数据：①=0.2，βi=12 h；②=0.4，βi=12 h；③=0.6，βi=12 h；④=0.2，βi=24 h。馈线、母线和变电站的平均故障率和修复时间来自文献[20]的真实系统数据。采用SAIDI，SAIFI和EENS指标评估含DG的配电系统可靠性。

图6显示了在4种DG可靠性数据下，配电网在增加DG前、后的可靠性指数结果。增加1个DG后，SAIDI，SAIFI和EENS指数分别降至17.983 6，1.776 3和67.945；增加2个DG后，SAIDI，SAIFI和EENS指数分别降至10.865 4，1.138 9和42.881。随着纳入配电系统DG数量的增加，可靠性指数均有所下降，系统平均中断时间和中断次数均会减少，从而提高了配电系统的供电量。供电量的增加将降低与未供应能量相关的EENS。

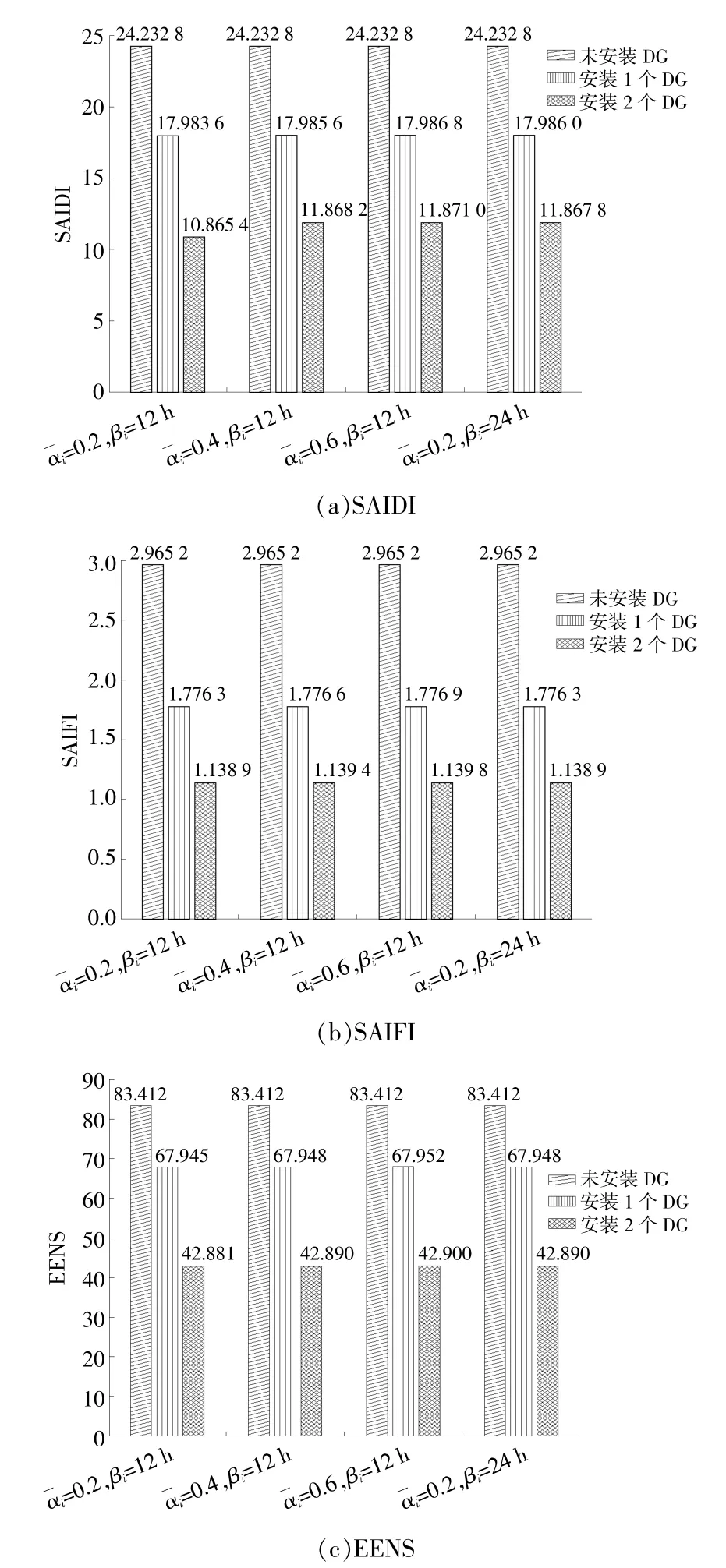
图6 不同故障率和修复时间对测试系统可靠性指数的影响Fig.6 Effect of different failure rates and repair time on the test system reliability index

4 结论

本文提出了一种基于马尔科夫过程蒙特卡洛法的可靠性评估模型。所提出的MCMC评价法适用于确定配电系统中DG的最优安装位置和容量，从而最大限度地降低实际功率、改善电压曲线和提高可靠性。综合分析了系统元件平均故障率和修复时间对SAIDI，SAIFI和EENS指标的影响，这些指标能够反映出智能电网的定义，即确定系统的自我修复、自我中断故障的能力。在含DG的IEEE-33节点配电网系统上对所提出的方法进行了测试，结果表明，该方法可以作为一种有效的测试工具，用于评估配电馈线的可靠性。