地形跟随中航迹跟踪模型预测控制方案设计

卜瑞宇, 王 彪, 李宏成, 唐超颖, 朱日楠

(南京航空航天大学自动化学院, 江苏 南京 211100)

0 引 言

随着地面与机载防空设施的日益完备,开展对先进低空突防技术的深入研究,并实现有效应用的意义逐步提升。地形跟随飞行[1]作为实现低空突防的关键技术之一,利用俯仰机动动作,使飞行器紧贴地形轮廓飞行,有效借助地球曲率与地形起伏造成的遮挡作为掩护,综合考虑与地形的贴近度和飞行机动性两方面要素,利用低空高速飞行完成任务。

地形跟随系统设计主要包括航迹规划、航迹跟踪、地形评估、传感器融合[2]等内容。一段时间以来,诸多学者对数字地图技术进行了卓有成效的研究。利用数字地图信息完成地形跟随任务的策略便于开展全局优化,此策略已成为当前主流的实现方案[3]。该方案的实现可分解为航迹规划与航迹跟踪两部分[4],即依据数字地图完成航迹规划,然后依据跟踪规划航迹完成飞行任务。本文重点关注航迹跟踪部分的研究,期望控制飞机跟踪参考航迹,尽可能实现跟踪误差最小化,对于航迹规划内容不做详细讨论。

在航空航天高带宽应用场景中,针对优化理论、控制理论的研究日益深入。单回路航迹跟踪经典控制方法如比例-积分-微分[5](proportional integral derivative, PID)控制、自抗扰控制[6],缺乏变量之间的耦合信息,对变量的硬约束简化为易于处理的输入约束,较难保证系统整体性能。模型预测控制(model predictive control, MPC)方便处理多输入多输出问题,具备直接处理约束的能力,不仅满足了实际应用需求,而且提供了较高的综合控制质量[7]。与常用的非线性控制方法,如滑模控制[8]、反步控制[9]相比,MPC有着滚动时域优化、实时反馈校正、协调目标分配等优势[10],对于控制指标变化、模型失配、系统干扰等情况的处理更加游刃有余。文献[11]在MPC框架内设计了直升机超低空飞行的轨迹优化策略,对地面、障碍物等保证了良好安全裕度。文献[12]在系统存在不确定性和动态干扰时,应用状态扩展双反馈MPC,能够实现对无人机侧向航迹稳定、准确的控制。同时,MPC的应用研究也不应忽视对闭环系统的稳定性分析,MPC因其有限时域滚动开展优化的实现形式,使得稳定性分析具有难度。自MPC诞生以来,针对其稳定性、闭环特性等的理论研究从未终止,文献[13]提纲挈领地将MPC稳定设计的要素提炼为:局部镇定控制器、终端集、终端代价函数。考虑到针对不同的MPC问题,设计与分析具有差异性,本文研究专注讨论所设计的航迹跟踪MPC控制器的稳定性问题。

地形跟随飞行需要在二维空间内实现精确的位置控制,时域参数作为MPC设计的主要优化决策变量[14],采用固定时域设置的MPC策略难以根据系统演化状态和运行趋势做出实时调整。近年来,关于自适应时域策略的应用讨论已在无人车辆循迹与蒸馏系统过程控制等领域逐步展开。文献[15]针对电动汽车路径跟踪问题,综合考虑动态稳定性和跟踪鲁棒性,实现时域长度在线切换,满足了对不同路径的跟踪控制需求。文献[16]在工业蒸馏控制中利用非线性规划灵敏度计算的结果在线更新时域长度,相比于固定时域的方法,能够保持良好的系统性能且计算时间可显著缩短。文献[17]结合强化学习对MPC方案的时域参数进行自适应调整,在倒立摆和碰撞避免系统中的应用显著改进了效果。自适应时域(adaptive horizon MPC, AHMPC)作为MPC策略的应用扩展,能够根据场景实时调整时域参数设计,而针对其在地形跟随领域的应用研究较为少见,本研究将关注AHMPC策略的设计与讨论。

整体而言,本文针对地形跟随飞行问题,设计了用于实现精确跟踪参考航迹的MPC控制器,并结合Lyapunov理论进行了控制器稳定性分析。接着,讨论并设计了航迹跟踪方法以及跟踪效果的综合评价策略。同时,考虑到地形跟随飞行时不同航迹段的跟踪需求差异,结合对MPC时域参数的应用影响分析,设计了时域参数切换的自适应方案。最后,在地形跟随飞行背景下进行了整体仿真验证和结果分析。

1 飞行器模型描述

本研究使用六自由度战斗机模型研究地形跟随飞行问题,飞机具体参数可参见文献[18]。小扰动条件下,对飞机运动进行纵垂向和横侧向的解耦和分组,可以得到本研究所需要的飞机纵向运动方程:

(1)

u=[δt,δe]T

(2)

式中:δt,δe分别代表油门开度、升降舵偏转。考虑水平稳态飞行条件对非线性模型进行配平,配平点为V=200 m/s,h=80 m,配平目标是从初始条件开始找到合适的输入使如下目标函数最小化:

(3)

式中:α,β为攻角和侧滑角;r为偏航角速度,然后在平衡状态下对飞行器模型进行线性化。

2 跟踪控制器设计与稳定性分析

2.1 MPC控制器设计

本研究航迹规划部分选择能兼顾飞机机动特性、航迹质量等要素的三次样条函数生成参考航迹的方案[19],通过求解规划问题来确定航迹曲线形状。整体控制框图如图1所示。

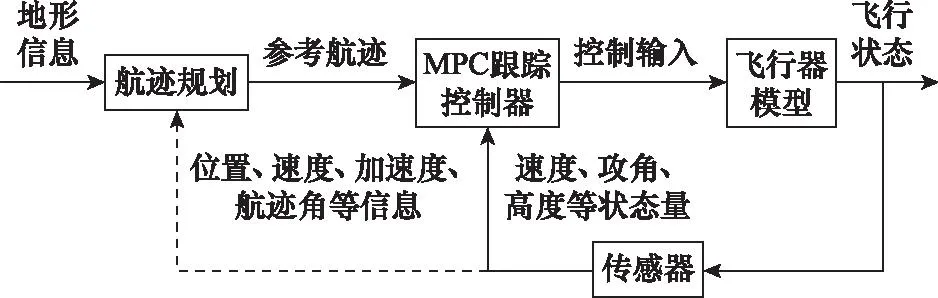
图1 整体控制框图Fig.1 Block diagram overall control

将被控对象按一定的采样周期进行离散化后的状态方程为

(4)

式(4)中的状态量、输出量和控制量依次为

其中,pow表示发动机功率;h为飞行高度。

MPC在处理增量式问题时具有天然优势,且方便引入积分,有助于消除静态误差,控制器设计采用状态增广形式,包含“预测模型”等要素的设计流程公式表达可参见文献[20]。

在本研究的应用中,由于系统未来的控制增量未知,需要构建考虑跟踪误差以及控制增量的目标函数,并对其进行求解,才能获得最终的优化控制序列ΔU*(k),目标函数表达式为

(5)

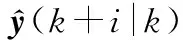
进一步地,将目标函数整理为二次型的形式:

J(x(k),ΔU(k))=[ΔUT(k),ε]THk[ΔUT(k),ε]+
Fk[ΔUT(k),ε]+Pk

(6)

(7)

同时,需要满足的控制增量、控制量、输出量约束为

(8)

式中:Δumin和Δumax分别表示控制时域内控制增量约束阈值;umin和umax分别表示控制时域内控制量约束阈值;ymin和ymax为输出约束阈值;i=0,1,…,Nc-1;j=1,2,…,Np;εmax为松弛因子阈值。引入松弛因子后,当优化问题不存在可行解时,松弛因子会自动扩大约束范围,尽可能获取优化解[21]。

求解式(7)表述的二次规划问题可以得到优化控制序列:

ΔU*(k)=[Δu*(k|k),Δu*(k+1|k),…,
Δu*(k+Nc-1|k)]T

(9)

ΔU*(k)是关于预测时域、控制时域、测量值x(k)的函数,且是非线性的关系[22]。根据MPC的基本原理,得到的开环控制序列的第一步作用于系统,下一个采样时刻,将用新的测量值更新约束优化问题,重新求解二次规划问题,作用于系统的控制量为

u*(k)=u*(k-1)+Δu*(k|k)

(10)

2.2 稳定性分析

对于最优控制问题,往往选择其目标函数作为展示系统Lyapunov稳定性的一个理想函数[23]。最优控制作为MPC最为重要的理论参考,Lyapunov稳定性分析方法同样作为MPC性能保证的基本策略,但由于MPC只在有限时域内考虑最优控制问题,相邻时刻的优化问题在MPC框架下是相互独立的,相邻时刻的目标函数可比性和关联性弱,约束的存在又使得闭环系统展现出非线性特性。对于不同的MPC问题,难以采用通用的分析方案,而Lyapunov第二稳定性定理通常用于证明此类系统稳定性问题[24]。

定理 1对于用离散化状态空间模型描述的被控对象,应选取合适的Q,R、预测时域(Np≥1)、控制时域(1≤Nc≤Np),确保优化问题有解。选取k时刻目标函数J*(k)作为Lyapunov函数,在k+1时刻,若满足J*(k+1)≤J*(k),那么ΔU*(k)就能保证系统的稳定。

证明借助最优控制稳定分析的思路,将每一步滚动优化得到的优化序列ΔU*(k)所对应的目标函数J*(k)作为Lyapunov函数V*(k)进行稳定性分析,表述为

(11)

根据MPC的基本特点,得到的开环控制序列仅第一步作用于系统,在下一个采样时刻,将用新的测量值刷新约束优化问题。从实现条件出发,将未作用于系统的控制增量序列充分利用,建立k时刻与k+1时刻的中间过渡关系:

(12)

ΔU(k+1)为引入的k+1时刻的中间过渡解,前Nc-1个序列分量由ΔU*(k)中分量移位得到,中间过渡解ΔU(k+1)对应的目标函数值为J(k+1)。图2为k时刻与k+1时刻的控制序列关系示意图,其中蓝色实线表示k时刻的控制增量优化序列ΔU*(k),蓝色虚线表示式(12)所构造的中间过渡解ΔU(k+1),黑色实线表示k+1时刻重新求解所得到的优化增量序列ΔU*(k+1)。ΔU(k+1)与ΔU*(k)的分量关系可表述为

图2 控制序列关系Fig.2 Relationship of control sequence

Δu(k+i|k+1)=Δu*(k+i|k),
i=1,2,…,Nc-1

(13)

中间过渡解ΔU(k+1)对应松弛因子与优化序列ΔU*(k)对应松弛因子的关系为

ε(k+1)=ε*(k)

(14)

注意到:除了ΔU*(k)与ΔU(k+1)的首项和末项不同外,其余各项均相同,这就使得产生的状态序列轨线也相同,那么目标函数J(k+1)与J*(k)由于存在诸多相同项而变得易于计算、比较[23]。

中间过渡解ΔU(k+1)对应的状态序列和输出序列为

(15)

(16)

其中,x*(k+i+1|k)和y*(k+i+1|k)为k时刻ΔU*(k)所对应的状态序列和输出序列。

式(15)和式(16)满足控制器的约束设置,k+1时刻的中间过渡解对应的目标函数值J(k+1)为

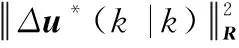
(17)

将J*(k)代入式(17),式(17)可进一步改写为

(18)

中间过渡解ΔU(k+1)满足式(8)的约束关系,且目标函数值J(k+1)有界,故ΔU(k+1)是k+1时刻优化问题的可行解[25],根据优化解与可行解对目标函数取值的影响,总存在如下关系:

J*(k+1)≤J(k+1)

(19)

进一步地,可以得到:

J*(k+1)≤J(k+1)≤J*(k)

(20)

对于任意k(k≥0),目标函数J*(k)总是单调递减的,松弛因子的引入进一步保证了递推的可行性。故选取J*(k)作为Lyapunov函数可以保证系统稳定。

证毕

3 误差评价与自适应时域方案设计

3.1 误差评价方法设计

对于本文所研究的航迹跟踪问题,在惯性坐标系内选取参考航迹点,根据当前位置和速度矢量,利用欧拉法对参考航迹点进行计算,是惯性系下进行航迹跟踪及跟踪误差计算的主要做法[26]。在有限时域内利用MPC计算参考航迹点的方案设计如图3所示,其中ΔT为系统采样时间,hi(i=1,2,…,Np)为预测时域内参考航迹点的离地高度,pi为i时刻的飞机离地高度,hi与pi的差值表示惯性系下的跟踪误差。

图3 惯性系下跟踪控制与误差评价示意图Fig.3 Schematic diagram of tracking control and error evaluation in inertial frame

由于飞行中爬升和俯冲动作频繁,本研究利用MPC前视预测能力,进行了机体系下的航迹跟踪及误差评价方法设计,机体系下误差评价设计示意图如图4所示。由图3和图4中的几何关系,可以得到在预测时域内惯性系与机体系评价跟踪误差的关系式:

图4 机体系下误差评价示意图Fig.4 Schematic diagram of error evaluation in body system

hi=pi+iVΔTsinγ+ei

(21)

式中:i=1,2,…,Np;ei为待确定参数,表示有限时域内机体系下的跟踪误差。

用相邻的预测跟踪误差与行进距离的关系表示航迹角的预测偏差量λi有:

(22)

γi=γ+λi

(23)

式中:γi表示惯性系下预测时域内航迹角的预测值。有限时域内的纵向位移信息用pn(i)表示:

pn(i)=pn+iVΔTcos(γ)

(24)

其中:i=1,2,…,Np;pn为当前时刻的纵向位移数据。

为方便表述,当γ为角度制单位且角度较小时,认为存在sinγ=γ/57.3,等式右侧为弧度制下的航迹角大小。结合式(21)、式(22)、式(23)可以得到惯性系与机体系下跟踪误差评价的转换关系矩阵:

(25)

式中:

xe(k)=[V,a,q,θ,pow,h,V1,γ1,h1,…,VNp,γNphNp]T

xb(k)=[V,a,q,θ,pow,h,Vr1,λi,e1,…,VrNp,λNp,eNp]T

式中:Vi=Vri(i=1,2,…,Np);xe(k),xb(k)均为增广向量;I6×6与I3Np×3Np为6×6维和3Np×3Np维的单位矩阵;0为维数相容的零矩阵。

同时,采用最大跟踪超调edmax、最大跟踪滞后edmin、平均跟踪误差edm、跟踪标准差eds、航迹角偏差eγm衡量飞行跟踪精度。为避免出现上述多个参数间评价效果不均的情况,设计用于评估地形跟随飞行中产生的航迹角、航迹跟踪误差的综合指标函数。根据函数中各评价参数的量纲关系,设置权重系数,综合评价函数表述为

Sw=W1edm+W2eds+W3eγm+W4edmax+W5edmin

(26)

式中:W1,W2,W3,W4,W5为各评价参数的对应量纲系数。Sw越小说明整体航迹跟踪效果越好。

3.2 自适应时域方案设计

与其他利用MPC进行轨迹跟踪控制(如无人车辆控制[27]、船舶控制[28]等)相比,地形跟随飞行更具有挑战性,这体现在飞机必须与地形保持最小的安全距离,并以足够快的速度移动,以最大限度地降低被发现或跟踪的可能性。

MPC航迹跟踪控制设计中的主要参数包括采样时间Ts,预测时域Np,控制时域Nc,状态权重阵Q与控制权重阵R。这其中,采样时间与系统反馈效率和优化要求相关联。Q,R作为软约束,允许存在一定的偏离,Q反应了对不同时刻输出误差的重视程度,R则是对控制增量的剧烈变化施加适度抑制,均对系统作用有限。时域参数Nc体现了控制作用的能力和自由度,与在线优化计算量关系紧密;时域参数Np的设置需要关注未来时域内输入变化产生的稳态影响,与系统实际性能紧密关联。经过遍历调整参数后发现:Np越大,系统获取的未来时域内的前视状态信息越充足,越有益于飞机做出预先判断,Np过大时,飞机当前位置较近处的跟踪偏差会增大;Np过小时,无法及时控制,会出现失控情况。Nc的设置与Np的取值联系紧密,Nc过小时,在每个采样时刻难以紧密跟踪参考航迹;Nc过大时,控制动作频繁,计算复杂度提高。Np,Nc取值对地形跟随飞行中航迹跟踪的影响示意图如图5所示。

图5 时域参数对航迹跟踪影响示意图Fig.5 Schematic diagram of influence of time domain parameters on trajectory tracking

地形跟随飞行时山峰可能连续出现,地形频率变化迅速。由于利用三次样条函数航迹规划得到的参考航迹曲率平滑连续,较小的曲率下航迹跟踪相较曲率更大时的航迹跟踪更为容易。结合文献[29]的先验研究,在稳定速度方案下,设计适合航迹跟踪的随地形曲率自适应调整时域的方案,考虑地形跟随中的两种场景:

情景 1违反地形曲率约束,调节产生的控制饱和,设计自适应律为

(27)

式中:k为地形曲率;L1=(kM/kmax)8×(2/kmax),round为取整函数;N1为基础时域参数;kM为每一航迹段最大曲率;kmax为飞行器机动能力所能满足的曲率约束最大值。

情景 2满足地形曲率约束,随曲率轮廓自适应调整预测时域以提高跟踪精度,设计自适应律为

(28)

式中:L2为曲率增益系数;N2为基础时域参数。

情景1和情景2的应用差别在于如果在飞行中违反曲率约束,情景1通过适当增加预测时域减小产生的控制饱和影响。如果满足曲率约束设置,情景2的设置就用于提高跟踪控制器阻尼,在航迹变化快速时,减少飞行器跟踪响应的超调,提升航迹跟踪精确度。由于预先规划考虑了地形曲率约束,后续主要进行针对情景2的研究讨论。

4 仿真验证与结果分析

4.1 地形数据和仿真参数设置

使用的地形数据来自于地理数据云平台,飞行区域在沿飞行方向的一个纵向剖面内,考虑飞机下方为一个二维地形曲线,选取能够反映地表特征的地形剖面曲线进行仿真,地形全程60 km,地形标准差为184.97 m,地形坡度与曲率信息如图6所示,曲率最大值为0.001 4 m-1。

图6 坡度、曲率数据Fig.6 Slope and curvature data

在真实地形背景下,固定时域参数选取需要能保证控制器的实时性,满足自动地形跟随飞行的要求,且不发生飞行失控和航迹跟踪失败的情况。结合第3.2节的讨论,通过局部遍历MPC设计关键控制参数,预测时域Np区间范围选择为20≤Np≤30,控制时域Nc=6。

设置MPC控制器采样周期Ts=0.1 s,参考飞行速度V=200 m/s,初始飞行高度h=80 m。曲率增益系数L2=2 500,基础时域参数N2=25,软约束Q=diag[0.05,0.003],R=diag[2 000,25],权重系数ρ=1 000。式(26)中综合评价函数权重系数W1=10,W2=10,W3=100,W4=1,W5=1。离地安全高度为50 m,油门开度约束为[0,1],油门开度控制增量约束为[-0.2,0.2]。以一阶惯性环节表示升降舵动态变化,偏转幅度约束为[-25°,25°],升降舵控制增量约束为[-6°,6°]。

4.2 固定时域方案与自适应时域方案对比实验

本节进行固定时域MPC方案与第3.2节所设计的自适应时域MPC方案在地形跟随航迹跟踪控制中的仿真研究,为能在较大范围内了解时域参数选取对系统性能的影响,选择固定时域Np=20,25,30,自适应调整预测时域结果如图7所示。

图7 预测时域自适应调整Fig.7 Adaptive adjustment for predictive horizon

航迹角控制是实现准确航迹跟踪的必要前提,图8展示了不同时域参数设置下航迹角跟踪的整体效果。局部放大图显示,自适应方案相比于固定时域方案角度跟踪精度更高,航迹角误差更小。

图8 不同参数选择下航迹角跟踪效果Fig.8 Flight-path angle tracking effect with different parameter selection

图9展示了速度控制效果,整体来看,飞行速度均稳定在参考速度200 m/s附近,在飞越山峰和长低谷时有轻微变化。在Np=20和Np=25设置下局部速度振荡明显,对应参数下的空速稳定能力略显不足。

图9 不同参数选择下速度控制效果Fig.9 Speed control effect with different parameter selection

图10给出了不同时域参数设置下控制增量变化的结果,控制增量、油门开度、升降舵偏转角的变化结果如图11和图12所示,控制增量与控制量动态变化均在预设约束范围内。本研究主要通过油门开度控制飞行速度,通过升降舵控制飞行高度。由于采用了稳定速度控制的策略,在地形跟随飞行中出现航迹跟踪误差与速度控制偏差后,控制器按需调整油门开度和升降舵偏转角,缩小误差的动作产生了局部较大的控制量。在飞行时间[150,170]内出现了油门开度满约束的情况,结合速度控制的结果可以看到,对应的航路段附近速度控制偏差较大,此时飞机下方的地形连续变化,飞行爬升高坡时间较久,但油门开度能够在较短的时间内脱离饱和状态,对发动机等关键部件影响较小。同时可以看到,相同时间段内升降舵局部偏转剧烈,对应于出现的地形跟随飞行颠簸和速度控制精度不足的情况。

图10 控制增量变化结果Fig.10 Results of control incremental changes

图11 不同参数选择下的油门开度Fig.11 Throttle opening with different parameters selection

图12 不同参数选择下的升降舵偏转Fig.12 Elevator deflection with different parameters selection

图13展示了不同时域参数设置下地形跟随飞行的整体效果, 图14展示了不同时域参数下的航迹跟踪误差统计情况,误差统计数据列在表1中。由于进行了预先航迹规划,如果控制飞机跟踪上参考航迹就能保证不发生飞行撞地的情况。

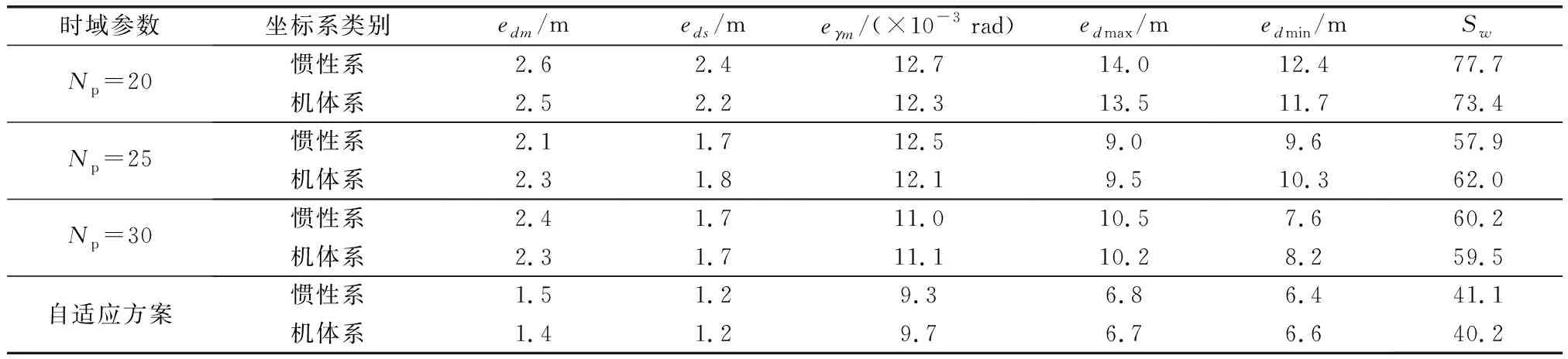
表1 误差统计数据Table 1 Error statistic data

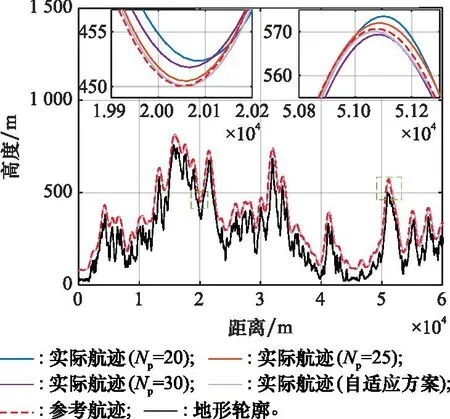
图13 不同参数选择下的地形跟随飞行效果Fig.13 Terrain following flight effect with different parameters selection

图14 惯性系及机体系下的跟踪误差Fig.14 Tracking error in inertial and body systems

根据惯性系和机体系跟踪误差统计结果分析,跟踪误差主要出现在连续飞越山峰阶段。地形曲率较小时,跟踪平滑流畅;地形曲率较大且飞行连续做出机动动作时,较小的时域参数Np=20,Np=25设置出现了局部姿态振荡、难以较快收敛误差等现象,影响了整体跟踪精度。Np=30相较较小的参数设置,跟踪滞后改善明显,误差标准差更小,数据波动小,但没能整体兼顾对跟踪超调的效果提升。

参考MIL-F-9490D对地形跟随飞行航迹跟踪误差的规范要求[30],跟踪超调不应超过15 m(安全高度的30%),跟踪滞后不应超过10 m(安全高度的20%)。结合表1中的数据可以看出:在稳定速度方案下,在预测时域参数Np=20设置下,由于系统获取的前视预测信息不足,跟踪超调与滞后处于较大的误差水平上,跟踪滞后不满足规范要求。预测时域设置需要充分考虑未来输出变化对系统产生的稳态影响,较大的预测时域虽然能够增大控制器阻尼,但是会减弱对当前位置附近的控制能力。在整体满足跟踪误差规范要求的前提下,Np=25与Np=30相比,edm,edmax数值更小,但针对跟踪滞后的改善,Np=25设置不如Np=30设置,所以单一调整固定时域参数较难整体把握对不同地形地段的跟踪要求。

在预设的5项评价指标内,自适应时域方案相较固定预测时域设置能够理想地满足误差规范要求,跟踪精度更高。惯性系下跟踪误差评价显示:跟踪超调edmax至少减少了24.5%,跟踪滞后edmin至少减小了15.8%,综合评价函数明显改善。机体系下的跟踪评价指标表现了飞行过程中出现的较小的姿态振荡和飞行颠簸,与固定时域设置相比,edm至少减小了39.2%,跟踪超调edmax至少减小了29.5%,兼顾飞行稳定性和跟踪精确性的综合评价函数也得到了有效改善。

尽管受飞机运动的约束限制,自适应时域方案对于海拔高度快速变化的地形展现出更精确的跟踪能力,兼顾飞行稳定性和跟踪精度的调整,反应更加灵敏,这得益于该方案能够有效结合未来的信息做出动作。但受限于局部线性化的近似误差、飞行器动态与控制器响应偏差,只能尽可能提升跟踪精度。

3组固定预测时域参数与自适应时域参数的平均求解时间Tmean(单位:ms)与最大求解时间Tmax(单位:ms)的统计数据列于表2,每一MPC步骤优化求解时间如图15所示。从表2和图15可以看出:随着预测时域的增加,优化求解时间总体呈现出增加的趋势,自适应方案的优化求解过程依然能够良好地满足系统实时性的要求。

表2 优化求解时间Table 2 Optimized solution time

图15 不同时域参数下的优化求解时间Fig.15 Optimized solution time with different parameters selection

4.3 速度与时域参数关系验证实验

考虑到地形跟随时飞机可能飞行在不同速度,第3.2节所讨论的稳定速度的方案简化了对用于反应控制自由度和能力的控制时域的讨论。作为对上述讨论的自适应策略的拓展和补充,在速度[120,280]m/s内,以步长20 m/s通过式(26)不同指标评价,遍历调整获得9组速度对应的较优的预测、控制时域。时域参数与飞行速度的曲线拟合关系如图16和图17所示。

图16 预测时域与飞行速度的拟合关系Fig.16 Fitting relationship between predictive horizon and flight velocity

图17 控制时域与飞行速度的拟合关系Fig.17 Fitting relationship between control horizon and flight velocity

经最小二乘拟合得到上述速度区间内时域参数与速度的关系为

(29)

其中,V∈[120,280]m/s。速度区间涵盖完整飞行速度包线,飞行速度在(200,280]m/s时,较小的预测时域不能满足对飞行稳定性和跟踪精度的要求,且此时较小的控制时域不能提供足够的控制灵敏度。飞行速度在[120,200)m/s时,较小预测时域和控制时域能有效保障对飞行转向和跟踪参考的要求。在高速飞行时增大时域参数能够满足飞行器对充足前视信息的要求,有益于做出预先反应。相比之下,在飞行速度较低时,对未来状态信息要求减少,在兼顾飞行稳定性和跟踪精度的同时,较小的时域参数设置便能较好地满足要求。

5 结 论

本文针对地形跟随飞行中航迹跟踪控制问题,设计了用于跟踪参考航迹的MPC控制器,并选取优化求解的目标函数作为证明系统稳定性的Lyapunov函数,证明了系统的闭环稳定性。考虑到地形跟随飞行是复杂、快速的动态过程,固定时域参数设置对于不同地形段适应力不足、跟踪整体效果不理想,以地形曲率变化为自适应切换时域的依据,设计了自适应调整时域的优化方案。同时,结合MPC前视预测能力,进行了惯性系和机体系航迹跟踪及误差评价方法设计。仿真验证结果表明,自适应方案相比于固定时域方案在地形跟随飞行时跟踪精度更高、综合效果改善明显,预设的性能指标能够对飞行全局效果进行有效评价。最后,作为对自适应时域切换方法的补充讨论,结合最小二乘拟合结果,分析了速度包线内速度与时域参数的调整关系。