基于自适应超螺旋观测器的空间机械臂鲁棒故障诊断
2024-03-27张海龙孔维国
高 升, 张海龙, 张 伟,*, 孔维国
(1. 中国科学院沈阳自动化研究所机器人学国家重点实验室, 辽宁 沈阳 110016; 2. 中国科学院机器人与智能制造创新研究院, 辽宁 沈阳 110169; 3. 航天器在轨故障诊断与维修重点实验室, 陕西 西安 710043)
0 引 言
随着在轨操作任务越来越复杂,对空间机械臂的需求也日益增多,其不仅可以协作或代替航天员完成舱外的操作任务,还可以完成在轨航天器或太空垃圾的捕获、空间载荷转移及在轨装配等任务[1]。然而,由于空间机械臂需要工作在太空环境中,所处环境复杂且恶劣,极易导致机械臂关节发生故障,影响机械臂在轨工作效率甚至出现机械臂彻底失去工作能力的情况。当机械臂关节发生故障后,应该及时给出警报,即及时检测出系统故障,以提高空间机械臂在轨操作的安全性与可靠性。因此,深入探究空间机械臂故障诊断方法显得尤为重要。自20世纪70年代以来,故障诊断技术得到了快速且深入的发展,已经成为一个热门且重要的研究领域[2-3]。
故障诊断方法随着现代控制理论的发展而逐渐壮大,目前故障诊断方法主要包括基于知识的方法、基于信号处理的方法、基于解析模型的方法及混合方法[4]。其中,基于解析模型的故障诊断方法研究最早也最成熟,与此同时,也是研究成果最多的方法。其起源于Beard的博士论文,即应用解析冗余代替硬件冗余。此外,基于观测器的故障诊断方法是基于解析模型方法最重要的分支,该方法基于系统的数学模型,可以发掘更多且更深层次的故障信息,因此也可以得到更准确的故障诊断结果。基于观测器的故障诊断方法主要包含残差生成和诊断策略两个过程,其基本思想是将系统的实际测量输出与观测器产生的估计输出进行比较,产生用于故障诊断的残差信息。理想情况下,当系统未出现故障时,残差信息为零或接近零值,但当系统出现故障时,残差远远偏于零值。然后,再结合设计的诊断策略完成系统故障诊断任务。本文也基于该思想设计可用于空间机械臂系统的故障诊断观测器。
考虑到空间机械臂较之地面机械臂的特殊性,需要开展针对性的研究工作。首先,空间机械臂工作于微重力环境中,即处于空间漂浮状态,因此在动力学模型与观测器设计方面不需要考虑重力项。其次,空间机械臂所处环境复杂,易受高层大气、太空中高能粒子及航天器振动等不确定因素的影响。因此,在处理系统故障诊断问题时,外部干扰对其影响更甚,有必要研究行之有效的鲁棒故障诊断方法,降低诊断的误报甚至错报率。常用的解决方案包括特征结构配置方法[5]、未知输入观测器方法[6-7]、H∞观测器方法[8]和滑模观测器方法[9]等。最后,由于空间机械臂的成本与重量限制,其一般不配备关节速度传感器,因此需要解决无角速度信息情况下的状态估计与故障诊断问题。常用的解决方案是设计滑模观测器,如终端滑模观测器[10]等。
由于滑模观测器对外部干扰的鲁棒性以及在状态估计方面良好的实用性,本文基于此技术开展研究工作。与此同时,超螺旋形式的观测器属于二阶滑模算法,其实是为了改善滑模观测器抖振现象而被提出的。其最早起源于文献[11],学者Levent基于相平面分析法给出了其稳定性证明方法,但该方法过于复杂且不利于理解。随着一类Moreno-Lyapunov函数[12]的发现,超螺旋观测器稳定性的证明得到了大大简化,并由此带动了一波研究热潮。在早期的研究中[13],虽然超螺旋观测器可以实现系统状态的有限时间估计,但基于等效输出获得的估计值是不连续的,需要额外引入低通滤波器以获得相应的连续结果,但低通滤波器的引入会导致时延现象,从而影响状态估计的效率。因此,学者们针对其平滑性进行了广泛研究[14-15]。另一方面,为了解决干扰噪声放大与估计项过估计问题,学者在经典超螺旋观测器的基础上引入参数自适应调整方法,提升了观测器的性能[16-18]。最后,为了进一步提升观测器性能,有学者将上述二者进行结合,提出了性能更为优异的自适应平滑超螺旋观测器[19]。
基于滑模观测器的故障诊断策略最早由学者Edwards提出并进行了深入研究[20],其主要原理是在估计误差到达滑模面后基于破坏滑动模态产生的残差信息进行故障诊断或基于等效输出注入项进行故障估计,本文基于前者进行研究。相比于其他有限时间观测器,如:齐次观测器、齐次反推观测器、终端滑模观测器,超螺旋观测器更符合工程实际,此外其还具有连续、易实现、理论分析严谨等优点。因此,自其提出之日起,便被广泛应用于干扰观测器设计[21-22]与自抗扰技术中的扩张状态观测器设计[23]。虽然文献[24-25]将其推广到了故障诊断领域,但观测器的性能有待进一步提升。同时,关于其应用于空间机械臂系统故障诊断的研究内容鲜有报道。因此,本文基于超螺旋观测器设计空间机械臂系统鲁棒故障诊断方法。
综上所述,针对空间机械臂系统,本文提出一种基于改进的自适应超螺旋观测器与自适应阈值的鲁棒故障诊断方法。与现有的超螺旋观测器相比,本文通过引入小于1的分数幂保证观测器的连续性与平滑性,避免了使用低通滤波器引起的时延对故障诊断结果的影响。与此同时,设计双层自适应律(参数自适应项)与快速趋近律(线性比例项),以进一步提升观测器的性能。双层自适应律的引入可以解决过估计与噪声放大问题,而快速趋近律的引入可以加快估计误差的收敛速度,改善故障诊断效果。本文基于Moreno-Lyapunov函数算法给出了有限时间稳定性的详尽分析及观测器的设计条件。最后,将本文方法应用于小行星采样空间三连杆机械臂算例,实现了复杂系统的鲁棒故障诊断,验证了该方法的有效性。
现将符号表示说明如下:Rn代表n维欧式空间。In代表n维单位矩阵,0代表常数零或适维零矩阵。‖·‖表示欧式空间范数。对于任意矩阵A,A>0表示矩阵A为正定矩阵。λmax(A),AT,A-1分别表示矩阵A的最大特征值、转置及逆。对称矩阵中,符号*表示通过对称得到的元素。最后,定义sig(x)a=[sign(x1)|x1|a,…,sign(xn)|xn|a]T,其中,sign(·)为符号函数,a为任意正实数。
1 系统介绍与问题描述
1.1 空间机械臂动力学模型
通用的n个关节空间机械臂动力学模型为
(1)


同时,动力学模型,即式(1),具有如下性质[10]。
性质 1M0(q)是对称正定矩阵且满足:
λ1‖x‖2≤xTM0(q)x≤λ2‖x‖2
(2)
式中:λ1和λ2为已知正实数。

(3)
式中:hΔ和ρd为未知上界值。

C0(x,y+z)=C0(x,y)+C0(x,z)
(4)
C0(x,y)z=C0(x,z)y
(5)
‖C0(x,y)‖≤cmax‖y‖
(6)
式中:cmax为可以确定的正实数。
关于性质3的详细推导过程可见文献[10]和文献[26]的相关研究内容。
1.2 执行器故障的数学模型
对于空间机械臂的操控而言,每个关节都由一个执行器驱动该关节绕轴旋转。关节通常由伺服电机、驱动器与减速器等组成,如图1所示。其中,第i个关节执行器的输入信号定义为uc_i(i=1, 2,…,n)表示关节驱动器的输出信号。与此同时,第i个关节执行器的输出扭矩定义为ui。

图1 空间机械臂各关节执行器通用示意图Fig.1 Generalized schematic diagram of actuator in each joint of space robot manipulator
在实际工作中,由于电机、减速器齿轮、连接线缆和驱动器的电子元件的损坏,空间机械臂执行器可能会发生故障/失效。这一问题大致可描述为:由于电机定子和转子之间摩擦的增加、轴承的边际故障、电机扭矩和电流驱动的减少以及齿轮间隙或驱动器故障等现象的发生,一个执行器可能出现偏置扭矩增加的故障,即扭矩偏差故障,以及部分效力丧失的故障。这两种类型的故障[27]可以表示如下:
ui=(1-δi)uc_i+Δui,i=1,2,…,n
(7)
式中:0%≤δi<100%表示第i个关节执行器部分效力丧失故障的失效因子;Δui表示扭矩偏差。值得说明的是,如果执行器i工作正常,则δi=0%,Δui=0;如果δi=30%,则表示执行器i失去30%的控制力矩。
基于式(7),空间机械臂关节驱动器的指令扭矩和关节执行器的输出扭矩之间的数学关系可以建立为
u=(In-E)uc+Δu
(8)
式中:
本文只考虑执行器扭矩偏差故障和部分失效故障。执行器的全失效故障(即δi=100%)和卡死故障(即ui输出一个恒定的值)不在本文的研究范围内。这是因为空间操作臂通常为串行连接的机械臂,对其关节驱动器一般不进行冗余设计。因此,当关节执行器出现上述两种形式的故障后,机械臂的动力学特性将被削弱并处于欠驱动状态,而机械臂的欠驱动控制不属于本文的研究范围。
1.3 问题描述
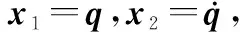
(9)
本文的目的是根据空间机械臂动力学模型式(9)设计鲁棒故障诊断方法,包括设计有限时间观测器与故障诊断策略,从而完成空间机械臂执行器的鲁棒故障诊断。
2 观测器设计
本文给出改进自适应超螺旋观测器如下:
(10)

(11)
式中:k>0表示常值控制参数,用于改善观测器的收敛性能(可以看成用特殊的快速终端滑模型趋近律代替原来的幂次趋近律);p为正常数,满足p∈(0.5,1)。此外,自适应增益项α(t)>0和β(t)>0的定义分别为
(12)
式中:α0和β0为正常数;j(e1,L(t))为时变项,可定义为
(13)
与文献[13]应用的经典形式的超螺旋观测器相比,本文提出的观测器在φ1(e1)和φ2(e1)中引入sig(e1)p与sig(e1)2p-1,以保证观测器的估计结果的连续性与平滑性,提升观测器估计的准确性。此外,与文献[16]和文献[18]提出的自适应超螺旋观测器相比,本文提出的观测器在其基础上设计了快速趋近律,即在φ1(e1)中引入额外的线性比例项ke1,以加快滑模面的收敛速度,在提高观测器性能的同时改善故障诊断效果。最后,j(e1,L(t))的引入可以简化观测器稳定性的证明过程。
当控制参数k=0时,即线性比例项ke1=0时,有限时间观测器式(10)退化为文献[28]提出的有限时间观测器。此外,当参数k=0及p=1时,有限时间观测器式(10)进一步退化为文献[29]提出的类Luenberger型观测器,即一种渐进收敛(指数收敛)观测器。
如果系统未出现故障,结合式(9)和式(10)可得到:
(14)

为了便于分析观测器的有限时间稳定性,定义状态向量如下:
(15)

(16)
又因为
(17)
成立,因此式(16)变为
(18)

与此同时,状态s2的导数为
(19)
根据α(t)和β(t)的定义,式(18)和式(19)可重写为如下更紧凑的形式:
(20)
为了进一步证明观测器的有限时间稳定性,给出如下定理。
定理 1针对式(9)系统设计自适应超螺旋观测器式(10),给定正常数ε,如果存在合适的增益参数α0,β0和对称正定矩阵P,使得
ATP+PA<-εP
(21)
成立,则系统估计误差满足有限时间一致最终有界,即观测器的估计误差会在有限时间T内收敛至包含原点的集合D内。其中,D={s:V≤Δ},Δ=(h1g3u-1)2p/(2p-1),u∈(0,1);有限时间T为
(22)
式中:符号h1和g3的定义将在后文给出。
证明定义Lyapunov函数为
(23)

进一步可得到:
(24)
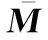
(25)

因此有:
(26)
根据式(21)可得到
(27)
应用性质3与文献[10]与文献[26]中的结果可知

(28)
进一步可得到:
‖ΔC0‖≤‖C0(x1,x2)‖‖e2‖+‖C0(x1,e2)‖‖e2‖+
‖C0(x1,e2)‖‖x2‖≤2cmax‖x2‖‖e2‖+cmax‖e2‖2≤
2cmaxk1‖e2‖+cmax‖e2‖2
(29)
结合式(3)和式(29)可知

(30)
式中:s=2(2cmax‖x2‖‖e2‖+cmax‖e2‖2)+2(hΔ+rd)


(31)
将式(31)简写为
(32)
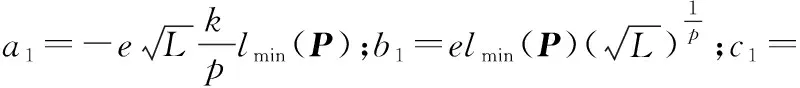
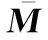
(33)
将式(33)代入式(32),可得

(34)

定义J=g2V(s0)(1-p)/2p及一个吸引域:
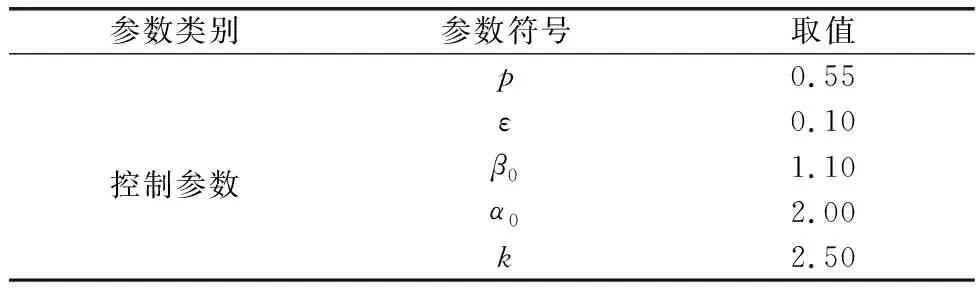
Ω={s:g2V(1-p)/2p (35) 系统的初始状态需要在吸引域Ω内,否则系统会不稳定。因此,可以得到0 (36) 式中:h1=g1-J>0。 进一步可得到: (37) (38) 因为p∈(0.5,1),则有(3p-1)/2p∈(0.5,1)。因此式(38)的形式表征系统的估计误差是有限时间一致最终有界的。这意味着,如果系统的估计误差初值在吸引域Ω内,则其会在有限时间T收敛至集合D,其中收敛时间T和集合D的定义已在文献[27]中给出。 证毕 如果在时刻tf系统出现执行器故障,则式(14)所表示的状态估计误差变为 (39) 由式(39)可知,当执行器故障为0时,系统进入理想的滑动模态后,观测器的估计误差对干扰是鲁棒的且会收敛到包含原点的邻域内。当出现执行器故障后,这种理想的滑动模态被打破。因此,估计误差e2敏感于系统的执行器故障,所以本文选择e2作为诊断执行器故障的残差信号。提出故障诊断策略如下: (40) 式中:‖e2‖RMS表示估计误差e2的均方根值;Jth表示故障诊断阈值。值得说明的是,该阈值是一种自适应诊断阈值,其是根据系统未发生执行器故障时估计误差e2的均方根值进行设计,可以有效提高故障诊断的准确性,降低故障诊断的误报率。 本文提出的自适应超螺旋观测器是基于超螺旋理论设计的观测器,超螺旋理论通常用于设计状态观测器或干扰观测器。在系统不存在干扰时,可以通过故障估计的形式实现故障诊断,但当系统存在干扰时,基于该理论设计的观测器便不再适用了。因此,本研究提出了基于残差信息的鲁棒故障诊断方案。值得说明的是,由于本文提出的观测器使用了自适应增益算法,所以当观测器的滑模运动被破坏后,系统的估计误差会在自适应算法的驱使下再次回到包含原点的邻域内,即生成的残差信息会再次被强制减小。因此,为了准确诊断出执行器故障,本文进一步提出了基于自适应阈值的故障诊断策略。 本文以小行星采样空间三连杆机械臂模型进行仿真校验分析。通过仿真模型验证本文所提出的故障诊断方法的有效性。 空间机械臂动力学模型及相关参数为 (41) (42) 应用定理1求得的观测器控制参数与采用的自适应参数[16]如表1所示。小行星采样空间三连杆机械臂的实际物理参数如表2所示。与此同时,机械臂3个关节的初值为q(0)=[0.2,0.1,-0.1]Trad,观测器的初始值都设置为0。 表1 观测器参数取值Table 1 Parameter values of the observer 表2 小行星采样空间三连杆机械臂物理参数Table 2 Physical parameters of the asteroid sampling space three-link robot manipulator 双层自适应算法的稳定性证明详见文献[16],这里不再赘述。此外,仿真中涉及的观测器自适应参数均取自其研究结果。 为了验证故障诊断算法的有效性,机械臂关节执行器的故障设置为:关节2:已知存在Δu1=0 N·m且δ1=0%,t<3 s,Δu1=-2.5 N·m且δ1=60%,t≥3 s。 首先,对本文所设计的观测器的有限时间估计性能进行仿真验证及性能分析。自适应超螺旋观测器的状态估计误差曲线如图2所示。从图2可以看出,观测器的估计误差可以在有限时间内收敛至包含0的邻域内,即稳态时间T约为0.2 s。因此,观测器的有限时间稳定性得到了证明。 图2 自适应超螺旋观测器状态估计误差Fig.2 State estimation error of adaptive super-twisting observer 为了进一步证明自适应超螺旋观测器在系统状态估计方面的优越性,将其估计性能与Edwards观测器[16]进行了比较,结果如图2、图3和表3所示。值得说明的是,对比仿真中,Edwards观测器采用的仿真参数除了性能控制参数k外,其他参数均与表2相同。从图2、图3及表3可以看出,两个观测器对干扰都有很好的鲁棒性,无论是eq的稳态精度或是ew的稳态精度均在同一数量级,说明了两个观测器优秀的抗干扰性能。此外,性能控制参数k的引入,加快了估计误差的收敛速度,即本文提出的观测器的状态估计误差收敛至包含0的邻域内的时间约为0.2 s,而Edwards观测器的状态估计误差收敛至包含0的邻域内或稳态区间的时间分别约为2 s。因此,本文提出的自适应超螺旋观测器的快速性得到了充分验证与说明。值得说明的是,本文的观测器虽然改善了快速收敛性能,但其代价是ew的瞬态峰值(绝对值)会增大。由表3可以看出,本文观测器的瞬态峰值是0.99,而Edwards观测器的瞬态峰值则是0.41。此外,如果将本文的算法用于控制器设计,可推测出控制器的快速响应的代价可能是能耗增加。 表3 观测器性能对比结果Table 3 Comparison results of observers performance 图3 Edwards观测器状态估计误差Fig.3 State estimation error of Edwards observer 接着,对本文所设计的基于自适应超螺旋观测器的故障诊断策略进行仿真验证及性能分析。系统出现执行器故障时的故障检测结果如图4和图5所示。从图4可以看出,观测器的残差值在故障发生后超过了设定的自适应检测阈值。因此,由故障诊断逻辑可知,观测器成功检测出了系统的执行器故障。从图5可以看出,由于采用了自适应阈值策略,测量噪声等并不影响故障诊断结果。此外,本文提出的观测器要与自适应阈值策略配合使用,并且只考虑出现如式(7)所示的执行器故障。如果系统出现未知形式的干扰且幅值与执行器故障幅值在同一数量级,则本文提出的故障诊断方法无法完成故障的有效诊断。值得说明的是,未知形式的外部干扰对故障诊断的影响仍是本领域的难题之一,同时,在设计故障诊断算法时考虑已知干扰仍是本领域的主流研究方向。 图4 执行器故障诊断结果Fig.4 Result of actuator fault diagnosis 图5 执行器故障诊断结果(测量噪声)Fig.5 Result of actuator fault diagnosis (measurement noise) 与此同时,为了说明自适应超螺旋观测器在故障诊断方面的优越性,将其故障诊断结果与Edwards观测器进行了比较,比较结果如图6和图7所示。可以看到,这两个观测器虽然都可以成功检测出执行器故障,但自适应超螺旋观测器取得了更快的响应速度和更好的检测结果。从图7的细节可以看出自适应超螺旋观测器的残差在约3.02 s处超过检测阈值,而Edwards观测器的残差在约3.2 s处才超过检测阈值。这是因为Edwards观测器为了得到平滑的估计结果而引入了低通滤波器,其会导致时延的产生,从而降低故障诊断的响应速度。由上述分析结果可知,自适应超螺旋观测器的性能得到了充分验证。因此,本文所提出的基于自适应超螺旋观测器的鲁棒故障诊断方法可以有效地解决空间机械臂关节执行器的故障诊断问题,并对系统干扰具有很强的鲁棒性。 图6 执行器故障诊断对比结果(0~10 s)Fig.6 Comparision of actuator fault diagnosis results (0-10 s) 图7 执行器故障诊断对比结果 (3~7 s)Fig.7 Comparision of actuator fault diagnosis results (3-7 s) 虽然理论上参数k的取值越大,收敛时间越短,但通过进一步仿真发现,如果其值过大,会影响算法的实际执行效率,影响在线故障检测效果。针对本文的仿真算例,参数k的取值范围为2≤k≤5,因此在实际使用时应根据系统情况酌情调整该参数的实际取值。 本文针对空间机械臂系统提出一种基于自适应超螺旋观测器的鲁棒故障诊断方法。该方法无需机械臂的角速度信息且对外界干扰具有很强的鲁棒性。基于Moreno-Lyapunov函数方法严格分析了观测器的有限时间稳定性,提出了残差生成方法并设计了基于自适应阈值的故障诊断策略。通过增加小于1的分数幂,改善了观测器的平滑性,与此同时,增加了线性比例项,提升了观测器的快速性。此外,该方法避免了低通滤波器的使用,解决了其带来的时延问题。在未来的研究中,应进一步考虑基于该观测器的故障定位、估计及容错控制问题。

3 故障诊断策略
4 仿真校验








5 结束语
