雷达、通信、干扰信号一体化检测识别技术研究

张汉伟,周秀珍

(中国船舶集团有限公司第七二三研究所,江苏 扬州 225101)

0 概 述

传统的雷达对抗和通信对抗,二者相互独立运行工作,其存在一定的局限性,每个设备都需要相互独立的天线、微波、接收处理等模块,造成了硬件设备的极大浪费,也导致了平台隐身性能的大幅度下降[1]。新一代电子侦察设备需要具备雷达侦察、通信侦察与干扰信号识别功能。雷达侦察的主要功能为监测区域范围内的电磁态势,在密集的电磁信号环境中实时完成雷达信号的截获、测量、分选、识别处理,为实施综合电子对抗提供电子支援;对已截获的雷达信号进行动态跟踪和参数实时更新,为电子干扰提供实时引导。通信侦察的主要功能是能对敌语音数据通信、指挥控制通信、战术数据链、敌我识别和塔康等辐射源信号进行搜索、截获、测向、分析识别,对已知信号样式进行解调、监听与记录,对未知信号样式进行中频采样与数字海量存储,建立并丰富通信情报侦察数据库。干扰信号识别的主要功能是对侦收的辐射源信号进行干扰识别,分辨出是雷达信号还是干扰信号,为指挥员决策提供信息支持。现在战场环境信号复杂多样,且信号频率相互交叠,如果按照传统的信号检测和分选方法较难将混叠的通信信号和雷达信号进行筛选,且在信号检测和信号处理时相互影响。

1 雷达信号与通信信号模型

1.1 雷达信号基本模型

电子侦察接收机侦收到的雷达信号一般是由信号和高斯白噪声两部分组成。其信号模型可以描述为：

y(t)=s(t)+v(t)=Aejφ(t)+v(t)

(1)

式中：s(t)表示雷达信号;v(t) 表示均值为0、方差为δ2的高斯白噪声;φ(t)表示相位函数;A表示信号的幅度值。

由于本文主要针对雷达信号的脉内特征进行仿真分析,因此不针对捷变等脉间特征不同的雷达,选取了常规脉冲雷达信号、线性调频雷达信号、相位编码雷达信号等常见的雷达信号作为研究对象。

(1) 常规脉冲信号

常规脉冲信号给定数学模型为：

v(t),0≤t≤T

(2)

式中：fc为起始频率;T为脉冲宽度;φ为初始相位。

常规脉冲的时、频域波形如图1所示。

(2) 线性调频信号

线性调频信号广泛应用于现代雷达系统,选择合适的脉宽和信号带宽可以达到合适的速度分辨力和距离分辨力,线性调频可以分为向上调频和向下调频。脉冲宽度为τ0,带宽为B,向上线性调频的瞬时相位可表示为：

(3)

(4)

典型的线性调频信号可表示为：

(5)

典型的线性调频信号的时域与频域波形如图2和图3所示。

图2 线性调频信号的时域波形

图3 线性调频信号的频域波形

(3) 相位编码雷达信号

相位编码信号的调制函数是1组离散的有限序列,相位编码信号的相位一般在0～2π之间[2],一般可表示为：

s(t)=a(t)ejφtej2πf0t=u(t)ej2πf0t

(6)

式中：u(t)=a(t)ejφt为复包络;φt为信号的相位。

假设ΔT为信号的脉宽,T为相位编码信号的中子脉冲宽度,相位编码信号的码长为子脉冲的个数。在高频波形中,相连子脉冲的相位反转点是否连续取决于子脉冲宽度T和载频的关系。通常用2种比较简单的方法表示二相编码信号为{ck}={-1,+1,-1,-1,+1,+1,+1} 或 {ck}={- + - - + + + }。如果二相编码信号采用二元序列{ck}表示,则二相编码信号复包络为：

(7)

式中：u1(t)为子脉冲的复包络;T为子脉冲宽度;N为子脉冲个数;ΔT为二相编码信号的持续时间。

利用δ函数的性质,上面公式可写为：

u(t)=

(8)

根据傅里叶变换的性质,可得到公式(9)和公式(10)。

(9)

(10)

由卷积定理可得,二相编码信号的频谱可直接表达为：

u(f)=u1(f)u2(f)=

(11)

二相编码信号的频谱为：

(12)

二相编码信号的时宽带宽积是由子脉冲数N决定的,这种信号的带宽B可通过选取子脉冲宽度T得到,而时宽可以通过选取子脉冲数N得到,所以二相编码信号的时宽和带宽是可以独立选取的,码元个数较多可以得到较大的时宽带宽积[3]。相位编码信号的时域与频域波形如图4所示。

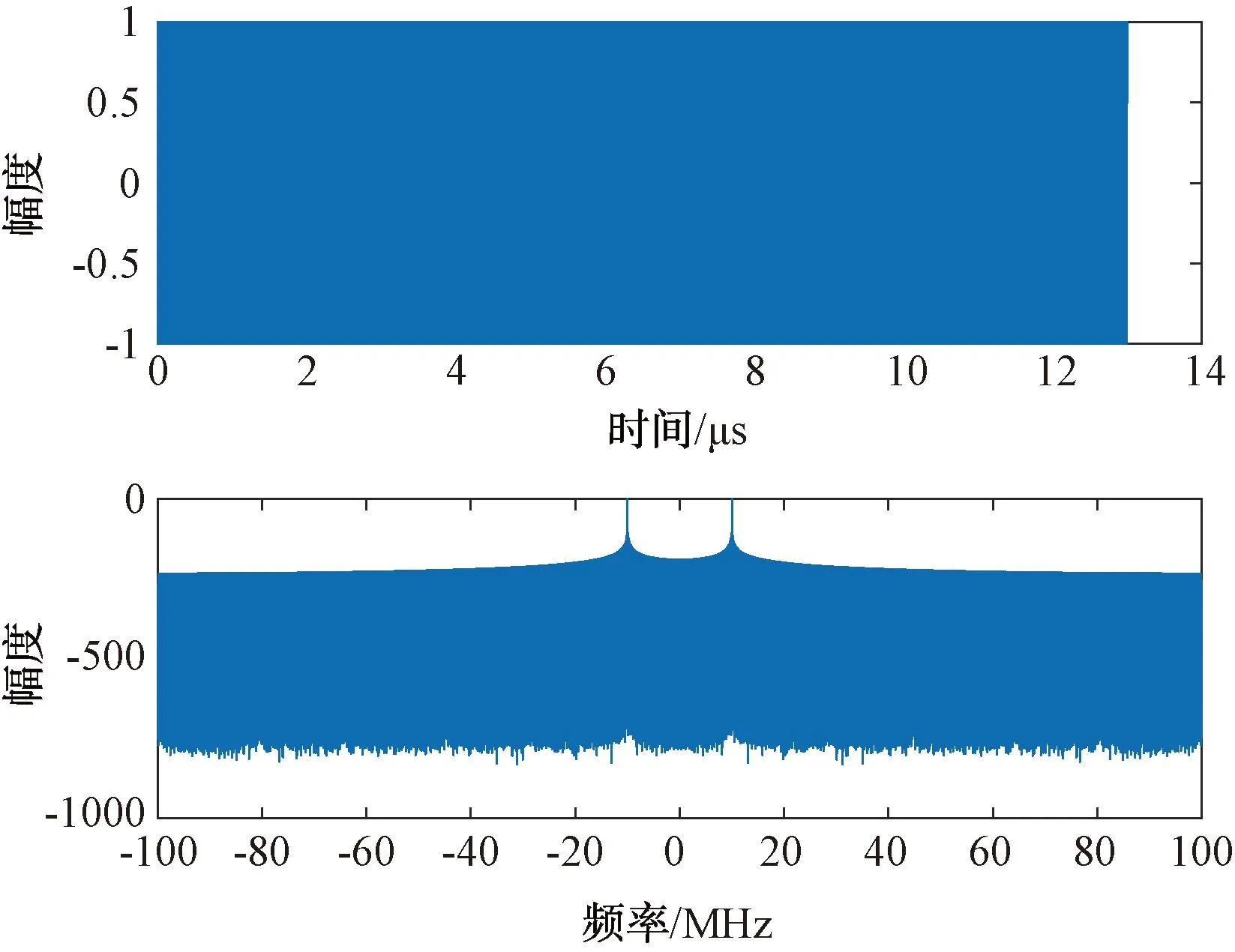
图4 相位编码信号的时域与频域波形

1.2 通信信号基本模型

本文所说的通信信号主要是指武协链、测控链等通信信号,通信信号的主要特点是信号带宽比较宽,信号幅度变化比较大,为准连续波信号。通信信号通常包含移频键控信号、移相键控信号、正交振幅调制信号。

(1) 移频键控信号：移频键控信号为调频正弦波信号,其中信号模型为：

(13)

式中：A表示脉冲信号幅度;g(t-iTb)表示信号宽度;(ωc+Δωi)t表示脉冲信号的角频率;φ表示初始相位。

(2) 移相键控信号：移相键控信号为调相正弦波信号,其中信号模型的表达式为：

(14)

式中：A表示脉冲信号幅度;g(t-iTb)表示信号宽度;ωct表示脉冲信号的角频率;φ表示初始相位。

(3) 正交振幅调制信号：正交振幅调制信号为调幅和调相正弦波信号,其中信号模型为：

s0(t)=g1(t)cos(ωct)-g0(t)sin(ωct)

(15)

式中：g1(t)和g0(t)表示脉冲信号;ωct表示角频率。

1.3 干扰信号基本模型

干扰信号按照类型可以分为压制性干扰和欺骗性干扰,压制干扰又可以分为阻塞干扰、瞄准干扰和扫频式干扰,欺骗干扰可以分为距离欺骗干扰以及角度欺骗干扰[4]。不同的干扰信号具有不同的频谱特性,通常把信号的频谱特性作为干扰信号特征分析和识别的主要依据。

噪声干扰的基本模型主要分为射频噪声干扰、噪声调幅干扰、噪声调频干扰等。

(1) 射频噪声干扰

它是通过对白噪声进行滤波及高频放大而直接产生的,因此又被称为纯噪声干扰,其数学模型可表示为：

J(t)=Un(t)cos(ω0t+φ(t))

(16)

式中：Un(t)为瑞利分布函数;φ(t)表示相位变化率,在[0,2π]内均匀分布,φ(t)与Un(t)独立分布;ω0为载频,载频的频谱宽度比J(t)大得多。

射频噪声干扰的功率谱密度函数为：

(17)

射频噪声干扰的时域频域波形如图5所示。

图5 射频噪声干扰的时频域波形

(2) 噪声调幅干扰

调幅信号是正弦波的幅度调制函数,噪声调幅干扰信号是用噪声对正弦波的信号进行调制,数学模型为：

J(t)=(U0+Un(t))cos(ω0t+φ)

(18)

其功率谱密度函数为：

(19)

调幅噪声干扰的时域、频域波形如图6所示。

图6 调幅噪声干扰的时频域波形

(3) 调频噪声干扰

调频信号是对正弦波进行频率调制,调频噪声干扰利用噪声的频率对正弦波进行调制,数学模型为：

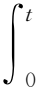
(20)

式中：u(t)表示噪声;φ表示相位,在[0,2π]内均匀分布,φ与u(t)独立分布;ω0表示载频,KFM表示斜率。

其功率谱模型为：

(21)

调频噪声干扰的时域、频域波形如图7所示。

图7 调频噪声干扰的时频域波形

2 雷达、通信及干扰信号联合检测仿真分析

根据雷达、通信和干扰信号的特点,一体化信号检测采取宽窄信道结合的方式,通过对模数转换器(ADC)数据的频谱分析进行干扰信号识别,利用频谱信息引导宽窄信道信道化接收机动态调制门限。宽窄信道信道化接收机对宽带采样信号进行宽信道信道化,对信号参数测量和调制方式粗测,提取雷达信号相应特征,形成脉冲描述字,发送至信号分选模块。对于子信道进行通信信号的参数测量和识别,信号处理流程如图8所示。

图8 雷达、通信、干扰信号一体化检测信号流程框图

2.1 雷达信号检测流程及模拟仿真

如图9所示,雷达、通信、干扰共用采样数据,雷达信号检测模块通过抽取后对采样数据进行数字信道化滤波。然后对所有子信道进行信号检测、参数测量以及调制方式测量,形成脉冲描述字(PDW)数据送综合分选与识别模块。当雷达信道的子信道存在通信信号时,对子信道进行抽取,进行通信信号的检测与参数测量。

图9 一体化信号检测中的雷达信号检测与参数测量

数字信道化接收机采用不同的滤波器组来处理不同频率的信号,数字信道化接收机具备对同时到达信号的处理能力,同时数字信道化也提升了接收机的灵敏度。但是由于ADC芯片的高采样率,导致数字信道化接收机的实时处理比较困难,一种等效的处理方法是在数字信道化之前对采样数据进行抽取,减轻后端处理的压力,这种采用抽取的形式进行数字信道化处理的方法称为多相滤波[5]。多相滤波是一种高效的数字信道化接收机的处理结构,它通过1组带通滤波器组取出不同的信号进行处理,其实现形式为：

(22)

式中：D为抽取因子;ωk,k=1,2,…,K-1(K为信道数),为各个滤波器组的中心频率。

对于均匀信道的偶型划分,低通滤波器组的信道化原理框图如图10,ωk=2πk/K,WK=ej2π/K,k=0,1,…,K-1。

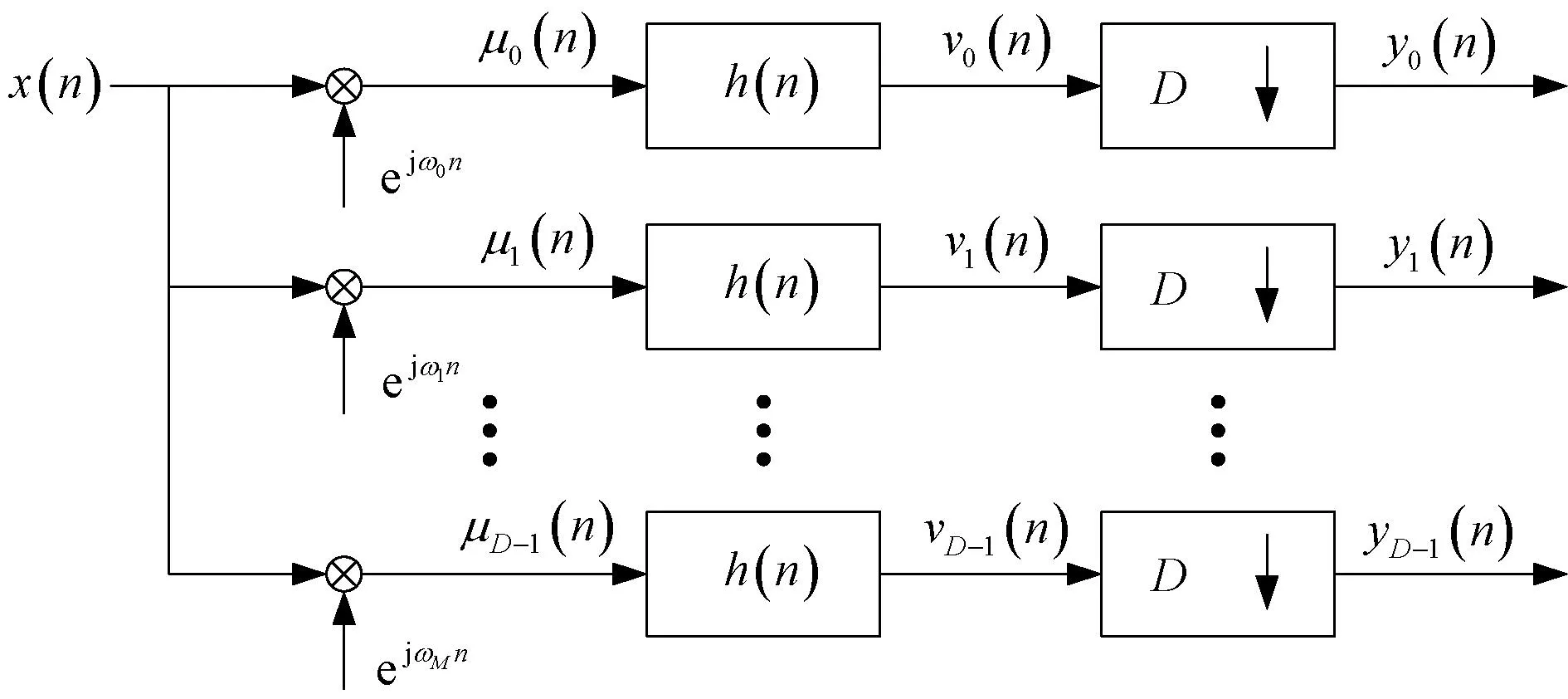
图10 低通滤波器组的信道化原理

令xi(m)=x(mD+i),hi(m)=h(mD-i),i=1,2…,D-1。其中hi(m)是h(n)的多相形式,对于临界抽样的情况,D=K,则有：

DFT[hi(m)*xi(m)]

(23)

由式(23)可得到多相离散傅里叶变换(DFT)滤波器组结构的信道化接收机,如图11所示。

图11 多相滤波器结构

多相滤波器的频率响应曲线如图12所示。

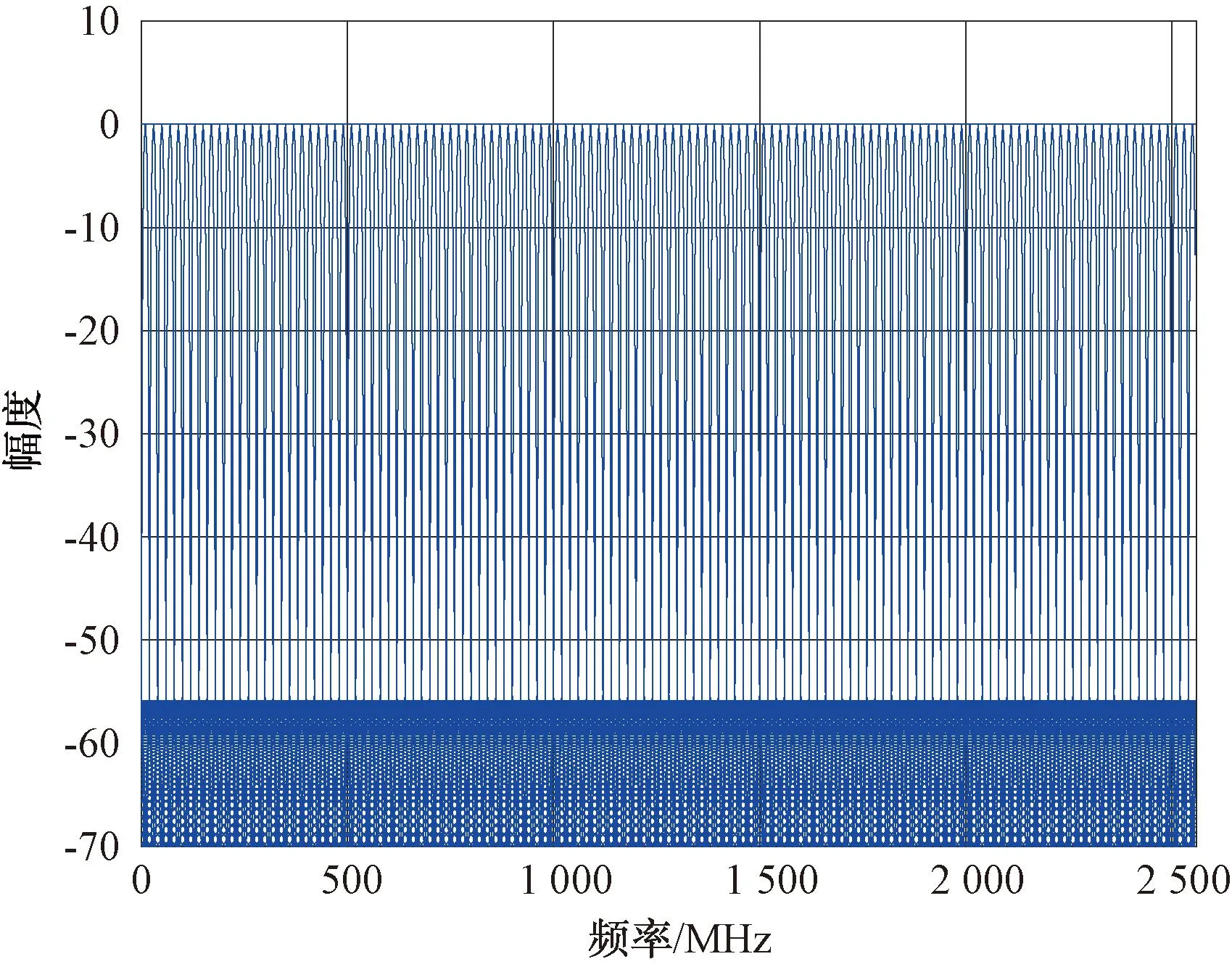
图12 多相滤波器频率响应

在信号检测中,为降低检测信噪比,提高对低功率信号的检测概率可采用相关积累算法提高积累增益[6],即：

xi=Aej(2πfciΔφ)+ωi,0≤i≤N-1

(24)

式中：A表示幅度;fc表示频率;Δt表示采样信号的时间间隔;φ表示初始相位;ωi为高斯白噪声。

对xi进行N点自相关运算可得：

(25)

其中：

(26)

N∝1时,ω′k服从其均值为0、方差为(2A2δ2+δ4/N)的高斯分布,相关积累的输出信噪比σ可表示为：

(27)

由式(27)可知,相关积累的积累增益在一定条件下与N成正比。

在20 MHz带宽下,常规脉冲信号的常规检测仿真结果如图13所示,采用64点相关积累检测的仿真结果如图14所示。

图13 常规检测信道化仿真波形

2.2 通信信号检测流程与模拟仿真

采样数据分为2路,对其中一路进行功率谱分析,另外一路进行数字信道化。当功率谱分析识别信号为连续波信号,对数字信道化的子信道进行窄带滤波,然后利用通信信号处理的方法进行信号特征提取和调试方式识别,流程图如图15所示。

对通信信号的特征提取主要通过时域、频域变换,变换域特征包括功率谱、谱相关函数、时域分布及其它参数。对于变换域特征,采用快速傅里叶变换(FFT)方法就能获取,而幅度、相位和频率等时域特征主要由Hilbert变换法、同相正交I-Q分量法、过零检测法等获取。

特征提取参数：幅度变化率a(t)、相位变化率φ(t)和频率变化率f(t),实信号x(t)可以表示为解析信号,即：

(28)

解析信号的瞬时幅度a(t)、瞬时相位φ(t)和瞬时频率f(t)分别为：

(29)

(30)

(31)

图16为3种不同类型调制信号的瞬时相位。

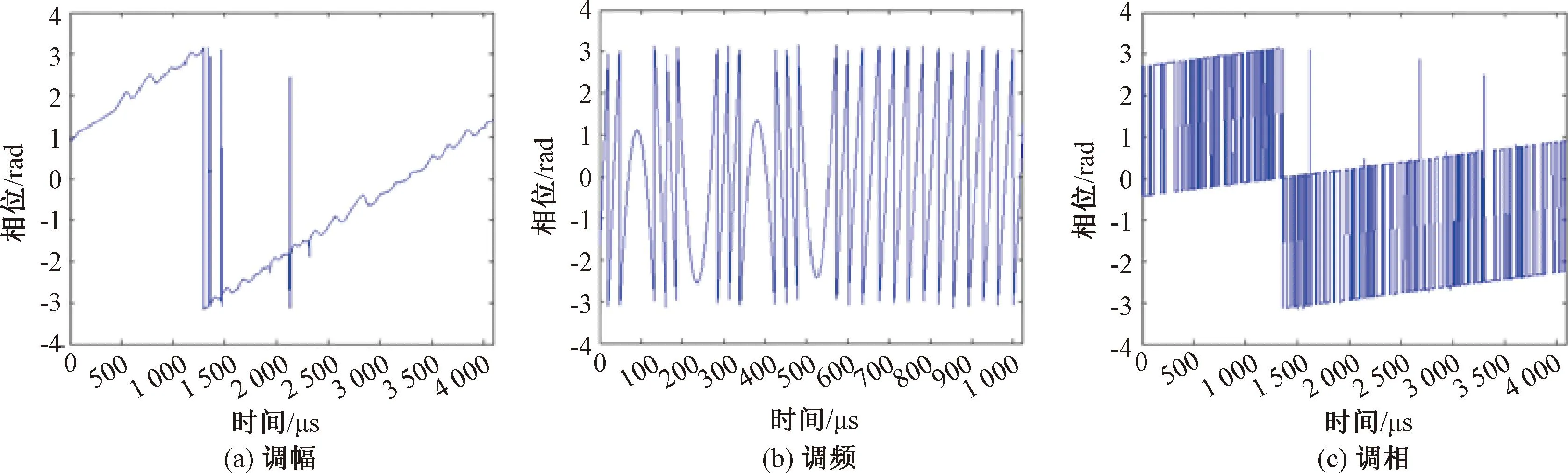
图16 3种不同类型调制信号的瞬时相位

2.3 干扰信号的识别仿真

如图17所示,对采样数据进行傅里叶变换和功率谱分析,根据干扰信号与其他信号的频谱特征对干扰信号进行分析和识别。

图17 干扰信号识别流程

典型梳状谱调频噪声干扰的时频分布如图18所示。

图18 调频噪声干扰的时频功率分布示意图

如图15所示,图中频率轴上凸起部分为与凹陷部分如梳子一般,随着时间延长。如果凹陷部分间距足够小,必须需要足够高的频率分辨率才可以分辨。因此,梳状谱模块需要对现场可编程门阵列(FPGA)输入时频功率谱及高分辨率功率谱同时分析,在确定干扰信号为宽带信号的情况下,进一步分析是否存在梳状凹坑,以确定是否存在此类型的干扰分析。首先,对时频功率谱进行时间轴的压缩,将当前重复周期内各信道所有数据累加,得到频率分布曲线,通过门限检测是否存在过门限的信道。如果过门限的信道连成一片或分布较宽,即可认为是宽带信号。在断定存在宽带干扰的情况下,分析已经过累加的高分辨率功率谱。检索出当前带宽内最高功率点的值,并以该值衰减3 dB作为门限基准,确定带宽内过门限的分布情况。如果存在有规律的凹陷,可判定为梳状干扰,并分析梳齿间隔,最终送识别结果综合模块进一步分析。

图19为采集数据的分析结果,图中用带阴影部分描述梳状谱的梳齿。

图19 梳状谱噪声调频干扰采集数据的频率功率分布直方图

3 结束语

随着信号环境的变化越来越复杂,雷达信号、通信信号、干扰信号在时频域重叠的现象越来越多,针对雷达、通信信号、干扰信号重叠时的信号一体化检测越来越重要。本为以雷达信号、通信信号和干扰的模型及特点为研究基础。提出了一种雷达信号、通信和干扰信号一体化检测的处理架构,并对雷达信号检测、通信信号检测和干扰信号识别进行了仿真,为工程实践和应用提供了一定的参考。